江苏省盐城景山中学2012—2013学年度第一学期高二数学月考试卷
文档属性
| 名称 | 江苏省盐城景山中学2012—2013学年度第一学期高二数学月考试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 175.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-18 00:00:00 | ||
图片预览




文档简介
盐城景山中学2012—2013学年度第一学期
阶段考试高二数学
一、填空题:本大题共14小题,每小题5分,共计70分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.
1. 函数的最小正周期是 ▲ .
2. 集合,,则 ▲ .
3.两根相距6m的木杆上系一根绳子, 并在绳子上挂一盏灯, 则灯与两端距离都大于2m的概率为 ▲ .
4 .经统计, 在某储蓄所一个营业窗口等候的人数及相应概率如下:
排队人数 0 1 2 3 4 5人及5人以上
概 率 0.1 0.16 0.3 0.3 0.1 0.04
则至少3人排队等候的概率为 ▲ .
5.已知向量且∥,则= ▲ .
6.等差数列中,若 HYPERLINK "http://www." , ,则 HYPERLINK "http://www." ▲ .
7.设、是两条不同的直线,、、是三个不同的平面,有下面四个命题:
① ;②;③ ;④.其中真命题的序号是 ▲ .
8.设x,y满足约束条件,则目标函数z=3x-y的最大值为 ▲ .
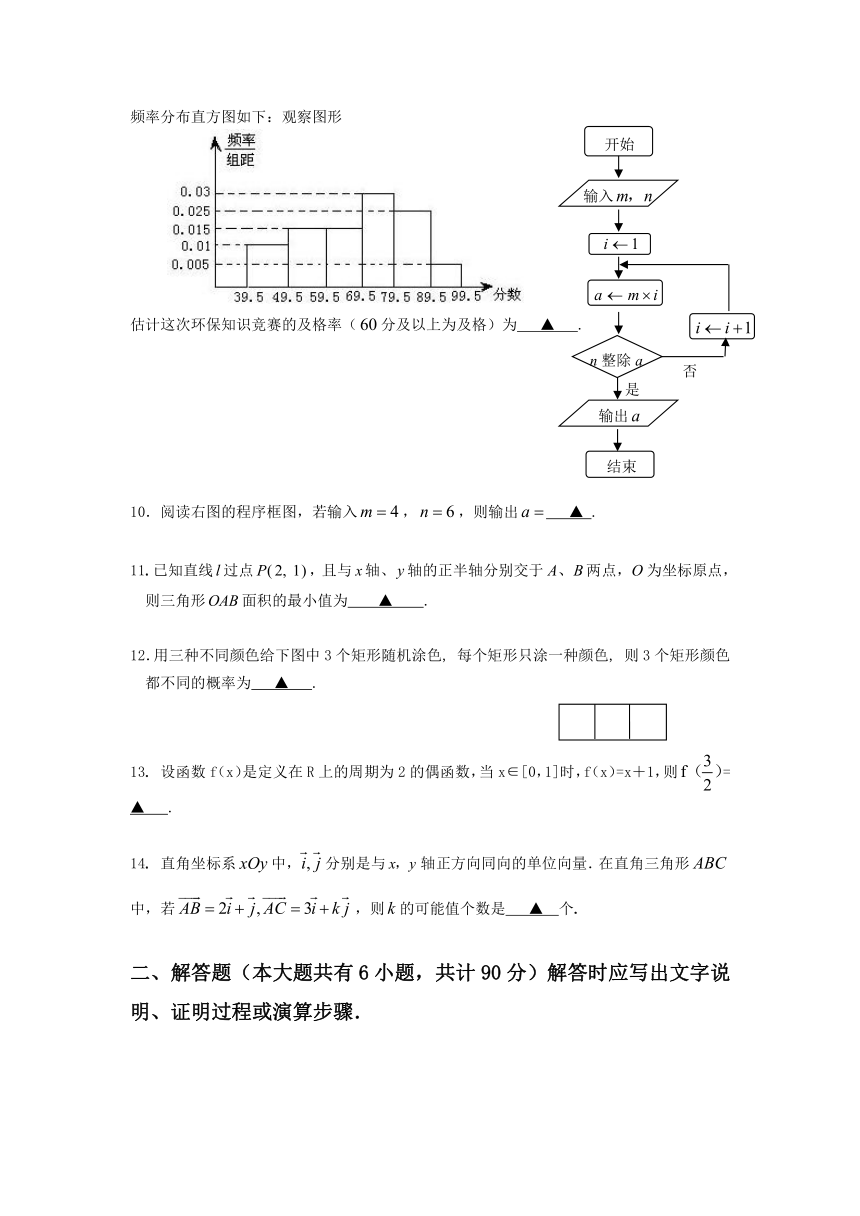
9 如图,从参加环保知识竞赛的学生中抽出名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形
估计这次环保知识竞赛的及格率(分及以上为及格)为 ▲ .
10.阅读右图的程序框图,若输入,,则输出 ▲ .
11.已知直线过点,且与轴、轴的正半轴分别交于两点,为坐标原点,则三角形面积的最小值为 ▲ .
12.用三种不同颜色给下图中3个矩形随机涂色, 每个矩形只涂一种颜色, 则3个矩形颜色都不同的概率为 ▲ .
13. 设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x+1,则= ▲ .
14. 直角坐标系中,分别是与轴正方向同向的单位向量.在直角三角形中,若,则的可能值个数是 ▲ 个.
二、解答题(本大题共有6小题,共计90分)解答时应写出文字说明、证明过程或演算步骤.
15.(本小题共14分)在△ABC中,BC=1,,
(Ⅰ)若,求AB;
(Ⅱ)若,求.
16.(本小题满分14分)
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(I)假设n=2,求第一大块地都种植品种甲的概率;
(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
品种甲 403 397 390 404 388 400 412 406
品种乙 419 403 412 418 408 423 400 413
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据的的样本方差,其中为样本平均数.
17.(本小题满分14分)已知 的值域为集合A,定义域为集合B,其中.
(Ⅰ)当,求;
(Ⅱ)设全集为R,若,求实数m的取值范围.
18. (本小题满分16分)如图,在长方体ABCD-A1B1C1D1 中,E,H分别是棱A1B1,D1C1上的点(点E与B1 不重合),且EH∥A1 D1. 过EH的平面与棱BB1 ,CC1 相交,交点分别为F,G。
证明:AD∥平面EFGH;
(Ⅱ)设AB=2AA1=2a .在长方体ABCD-A1B1C1D1 内随机选取一点。记该点取自几何体A1ABFE-D1DCGH内的概率为p,当点E,F分别在棱A1B1,B1B上运动且满足EF=a时,求p的最小值.
19.(本小题满分16分)已知⊙和点.
(Ⅰ)过点向⊙引切线,求直线的方程;
(Ⅱ)求以点为圆心,且被直线截得的弦长为 4的⊙的方程;
(Ⅲ)设为(Ⅱ)中⊙上任一点,过点向⊙引切线,切点为Q. 试探究:平面内是否存在一定点,使得为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
20. (本小题满分16分)
已知数列和满足:,其中为实数,为正整数.
(Ⅰ)对任意实数,证明:数列不是等比数列;
(Ⅱ)试判断数列是否为等比数列,并证明你的结论;
(Ⅲ)设,为数列的前项和.是否存在实数,使得对任意正整数,都有 若存在,求的取值范围;若不存在,说明理由.
盐城景山中学2012—2013学年度第一学期
阶段考试高二数学答题卷
一、填空题:(本大题共14小题,每小题5分,共70分.)
1、_______________; 2、_____________; 3、________________ ;
4、_______________; 5、_____________; 6、________________;
7、______________ ; 8、_____________; 9、________________;
10、______________ ; 11、_____________; 12、_______________
13、______________ ; 14、_____________.
二、解答题:(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.)
15.(本题共14分,第1小题满分7分,第2小题满分7分)
16.(本题共14分,第1小题满分7分,第2小题满分7分)
17.(本题共14分,第1小题满分6分,第2小题满分8分)
18. (本题共16分,第1小题满分6分,第2小题满分10分)
19. (本题共16分,第1小题满分5分,第2小题满分5分,第3小题满分6分)
20. (本题共16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)
盐城景山中学2012—2013学年度第一学期
阶段考试高二数学答案
1.2 ; 2. ;3. ;4 . 0.44 ; 5.;6. ;7. ①③ ;
8.5; 9 ( http: / / wxc. / ) ; 10.12; 11.4; 12. ;13. ; 14. 2
15.解:(Ⅰ)依题意:,
即,解之得,(舍去) …………7分
(Ⅱ),∴ ,,
∴ . …………14分
16.解:(I)设第一大块地中的两小块地编号为1,2,第二大块地中的两小块地编号为3,4,
令事件A=“第一大块地都种品种甲”.
从4小块地中任选2小块地种植品种甲的基本事件共6个;
(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).
而事件A包含1个基本事件:(1,2).
所以 ………………7分
(II)品种甲的每公顷产量的样本平均数和样本方差分别为:
………………10分
品种乙的每公顷产量的样本平均数和样本方差分别为:
………………13分
由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙. ……14分
17.解: ………6分
………10分
,此时成立. ……… 13分
综上所述,实数m的取值范围为. ……… 14分
18.解:
证明:在长方体ABCD-A1B1C1D1 中,AD∥A1 D1
又∵EH∥A1 D1 ,∴AD∥EH.
∵AD¢平面EFGH
EH 平面EFGH
∴AD//平面EFGH.
… 6分
设BC=b,则长方体ABCD-A1B1C1D1 的体积V=AB·AD·AA1 =2a2b,
几何体EB1F-HC1G的体积V1 =(EB1 ·B1F)·B1C1 =·EB 1 ·B1 F …9分
∵EB12 + B1 F2=a2
∴≤ = ,当且仅当EB 1 =B1 F=时等号成立
从而V1 ≤ . ……12分
故 p=1- ≥ 当且仅当EB 1 =B1 F= 时等号成立
∴p的最小值为 ………16分
19. 解:(Ⅰ)设切线方程为 ,易得,解得
…3分
∴切线方程为 …………………………………………5分
(Ⅱ)圆心到直线的距离为 ………………7分
设圆的半径为,则 …………………………………9分
∴⊙的方程为 ……………………………………… 10分
(Ⅲ)假设存在这样的点,点的坐标为,相应的定值为,
根据题意可得,∴…………………12分
即 (*),
又点在圆上∴,即,代入(*)式得:
……………………14分
若系数对应相等,则等式恒成立,∴,
解得,
∴可以找到这样的定点,使得为定值. 如点的坐标为时,比值为;
点的坐标为时,比值为…………………………………………16分
20.(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即
矛盾.
所以{an}不是等比数列. ……… 4分
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+21]=(-1)n+1(an-2n+14)
=(-1)n·(an-3n+21)=-bn
又b1=-(λ+18),所以
当λ=-18,bn=0,此时{bn}不是等比数列:
当λ≠-18时,b1=-(λ+18) ≠0,由上可知bn≠0,∴
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-为公比的等比数列. ……10分
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn= -(λ+18)·(-)n-1,于是可得
Sn=-
要使a即a<-(λ+18)·[1-(-)n]〈b
………12分
设
当n为正奇数时,1∴f(n)的最大值为f(1)=,f(n)的最小值为f(2)= ,
于是,得 a<-(λ+18)< ………14分
当a当b>3a存在实数λ,使得对任意正整数n,都有a且λ的取值范围是(-b-18,-3a-18). ………16分
开始
n整除a
是
输入
结束
输出
否
M
x
y
o
·
第19题
姓名:____________班级:____________学号:____________
阶段考试高二数学
一、填空题:本大题共14小题,每小题5分,共计70分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.
1. 函数的最小正周期是 ▲ .
2. 集合,,则 ▲ .
3.两根相距6m的木杆上系一根绳子, 并在绳子上挂一盏灯, 则灯与两端距离都大于2m的概率为 ▲ .
4 .经统计, 在某储蓄所一个营业窗口等候的人数及相应概率如下:
排队人数 0 1 2 3 4 5人及5人以上
概 率 0.1 0.16 0.3 0.3 0.1 0.04
则至少3人排队等候的概率为 ▲ .
5.已知向量且∥,则= ▲ .
6.等差数列中,若 HYPERLINK "http://www." , ,则 HYPERLINK "http://www." ▲ .
7.设、是两条不同的直线,、、是三个不同的平面,有下面四个命题:
① ;②;③ ;④.其中真命题的序号是 ▲ .
8.设x,y满足约束条件,则目标函数z=3x-y的最大值为 ▲ .
9 如图,从参加环保知识竞赛的学生中抽出名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形
估计这次环保知识竞赛的及格率(分及以上为及格)为 ▲ .
10.阅读右图的程序框图,若输入,,则输出 ▲ .
11.已知直线过点,且与轴、轴的正半轴分别交于两点,为坐标原点,则三角形面积的最小值为 ▲ .
12.用三种不同颜色给下图中3个矩形随机涂色, 每个矩形只涂一种颜色, 则3个矩形颜色都不同的概率为 ▲ .
13. 设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x+1,则= ▲ .
14. 直角坐标系中,分别是与轴正方向同向的单位向量.在直角三角形中,若,则的可能值个数是 ▲ 个.
二、解答题(本大题共有6小题,共计90分)解答时应写出文字说明、证明过程或演算步骤.
15.(本小题共14分)在△ABC中,BC=1,,
(Ⅰ)若,求AB;
(Ⅱ)若,求.
16.(本小题满分14分)
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(I)假设n=2,求第一大块地都种植品种甲的概率;
(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
品种甲 403 397 390 404 388 400 412 406
品种乙 419 403 412 418 408 423 400 413
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据的的样本方差,其中为样本平均数.
17.(本小题满分14分)已知 的值域为集合A,定义域为集合B,其中.
(Ⅰ)当,求;
(Ⅱ)设全集为R,若,求实数m的取值范围.
18. (本小题满分16分)如图,在长方体ABCD-A1B1C1D1 中,E,H分别是棱A1B1,D1C1上的点(点E与B1 不重合),且EH∥A1 D1. 过EH的平面与棱BB1 ,CC1 相交,交点分别为F,G。
证明:AD∥平面EFGH;
(Ⅱ)设AB=2AA1=2a .在长方体ABCD-A1B1C1D1 内随机选取一点。记该点取自几何体A1ABFE-D1DCGH内的概率为p,当点E,F分别在棱A1B1,B1B上运动且满足EF=a时,求p的最小值.
19.(本小题满分16分)已知⊙和点.
(Ⅰ)过点向⊙引切线,求直线的方程;
(Ⅱ)求以点为圆心,且被直线截得的弦长为 4的⊙的方程;
(Ⅲ)设为(Ⅱ)中⊙上任一点,过点向⊙引切线,切点为Q. 试探究:平面内是否存在一定点,使得为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
20. (本小题满分16分)
已知数列和满足:,其中为实数,为正整数.
(Ⅰ)对任意实数,证明:数列不是等比数列;
(Ⅱ)试判断数列是否为等比数列,并证明你的结论;
(Ⅲ)设,为数列的前项和.是否存在实数,使得对任意正整数,都有 若存在,求的取值范围;若不存在,说明理由.
盐城景山中学2012—2013学年度第一学期
阶段考试高二数学答题卷
一、填空题:(本大题共14小题,每小题5分,共70分.)
1、_______________; 2、_____________; 3、________________ ;
4、_______________; 5、_____________; 6、________________;
7、______________ ; 8、_____________; 9、________________;
10、______________ ; 11、_____________; 12、_______________
13、______________ ; 14、_____________.
二、解答题:(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.)
15.(本题共14分,第1小题满分7分,第2小题满分7分)
16.(本题共14分,第1小题满分7分,第2小题满分7分)
17.(本题共14分,第1小题满分6分,第2小题满分8分)
18. (本题共16分,第1小题满分6分,第2小题满分10分)
19. (本题共16分,第1小题满分5分,第2小题满分5分,第3小题满分6分)
20. (本题共16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)
盐城景山中学2012—2013学年度第一学期
阶段考试高二数学答案
1.2 ; 2. ;3. ;4 . 0.44 ; 5.;6. ;7. ①③ ;
8.5; 9 ( http: / / wxc. / ) ; 10.12; 11.4; 12. ;13. ; 14. 2
15.解:(Ⅰ)依题意:,
即,解之得,(舍去) …………7分
(Ⅱ),∴ ,,
∴ . …………14分
16.解:(I)设第一大块地中的两小块地编号为1,2,第二大块地中的两小块地编号为3,4,
令事件A=“第一大块地都种品种甲”.
从4小块地中任选2小块地种植品种甲的基本事件共6个;
(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).
而事件A包含1个基本事件:(1,2).
所以 ………………7分
(II)品种甲的每公顷产量的样本平均数和样本方差分别为:
………………10分
品种乙的每公顷产量的样本平均数和样本方差分别为:
………………13分
由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙. ……14分
17.解: ………6分
………10分
,此时成立. ……… 13分
综上所述,实数m的取值范围为. ……… 14分
18.解:
证明:在长方体ABCD-A1B1C1D1 中,AD∥A1 D1
又∵EH∥A1 D1 ,∴AD∥EH.
∵AD¢平面EFGH
EH 平面EFGH
∴AD//平面EFGH.
… 6分
设BC=b,则长方体ABCD-A1B1C1D1 的体积V=AB·AD·AA1 =2a2b,
几何体EB1F-HC1G的体积V1 =(EB1 ·B1F)·B1C1 =·EB 1 ·B1 F …9分
∵EB12 + B1 F2=a2
∴≤ = ,当且仅当EB 1 =B1 F=时等号成立
从而V1 ≤ . ……12分
故 p=1- ≥ 当且仅当EB 1 =B1 F= 时等号成立
∴p的最小值为 ………16分
19. 解:(Ⅰ)设切线方程为 ,易得,解得
…3分
∴切线方程为 …………………………………………5分
(Ⅱ)圆心到直线的距离为 ………………7分
设圆的半径为,则 …………………………………9分
∴⊙的方程为 ……………………………………… 10分
(Ⅲ)假设存在这样的点,点的坐标为,相应的定值为,
根据题意可得,∴…………………12分
即 (*),
又点在圆上∴,即,代入(*)式得:
……………………14分
若系数对应相等,则等式恒成立,∴,
解得,
∴可以找到这样的定点,使得为定值. 如点的坐标为时,比值为;
点的坐标为时,比值为…………………………………………16分
20.(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即
矛盾.
所以{an}不是等比数列. ……… 4分
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+21]=(-1)n+1(an-2n+14)
=(-1)n·(an-3n+21)=-bn
又b1=-(λ+18),所以
当λ=-18,bn=0,此时{bn}不是等比数列:
当λ≠-18时,b1=-(λ+18) ≠0,由上可知bn≠0,∴
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-为公比的等比数列. ……10分
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn= -(λ+18)·(-)n-1,于是可得
Sn=-
要使a
………12分
设
当n为正奇数时,1
于是,得 a<-(λ+18)< ………14分
当a
开始
n整除a
是
输入
结束
输出
否
M
x
y
o
·
第19题
姓名:____________班级:____________学号:____________
同课章节目录
