高二数学选修(2—2)阶段考试卷
文档属性
| 名称 | 高二数学选修(2—2)阶段考试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 127.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-18 08:38:55 | ||
图片预览


文档简介
高二数学选修(2—2)阶段考试卷
一、选择题:(每题5分共60分,每题有且仅有一个正确答案)
1、曲线在点处的切线方程为( )
A. B. C. D.
2.设,则( )
A. B.
C. D.
3.由抛物线与直线所围成的图形的面积是( ).
A. B.38/3 C.16/3 D.
4、5.函数的单调递减区间是( )
A.(,+∞) B.(-∞,) C.(0,) D.(e,+∞)
5.下面使用类比推理正确的是 ( )
A.“若,则”类推出“若,则”
B.“若”类推出“”
C.“若” 类推出“ (c≠0)”
D.“” 类推出“”
6.设是定义在整数集上的函数,且满足:“当成立时,总可以推出成立”。那么下列命题总成立的是( )
A.若成立,则当时均有成立
B.若成立,则当时均有成立
C.若成立,则当时均有成立
D.若成立,则当时均有成立
7.设, ,n∈N,则
( )
A. B.- C. D.-
8.如果10N的力能使弹簧压缩10cm,为在弹性限度内将弹簧拉长6cm,则力所做的功为( )
A.0.28J B.0.12J C.0.26J D.0.18J
9.已知 ,猜想的表达式为 ( )
A. B. C. D.
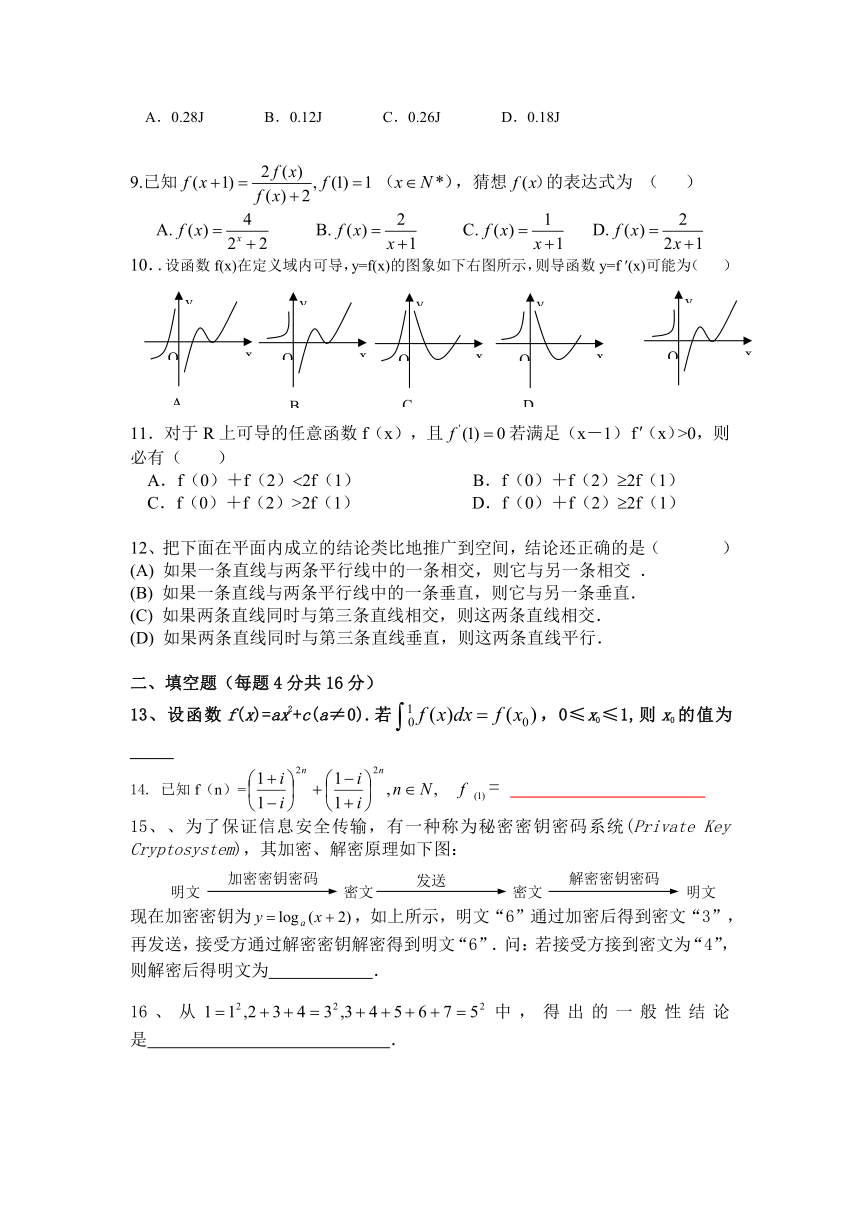
10..设函数f(x)在定义域内可导,y=f(x)的图象如下右图所示,则导函数y=f (x)可能为( )
11.对于R上可导的任意函数f(x),且若满足(x-1)>0,则必有( )
A.f(0)+f(2)2f(1) B.f(0)+f(2)2f(1)
C.f(0)+f(2)>2f(1) D.f(0)+f(2)2f(1)
12、把下面在平面内成立的结论类比地推广到空间,结论还正确的是( )
(A) 如果一条直线与两条平行线中的一条相交,则它与另一条相交 .
(B) 如果一条直线与两条平行线中的一条垂直,则它与另一条垂直.
(C) 如果两条直线同时与第三条直线相交,则这两条直线相交.
(D) 如果两条直线同时与第三条直线垂直,则这两条直线平行.
二、填空题(每题4分共16分)
13、设函数f(x)=ax2+c(a≠0).若,0≤x0≤1,则x0的值为_____
14. 已知f(n)==
15、、为了保证信息安全传输,有一种称为秘密密钥密码系统(Private Key Cryptosystem),其加密、解密原理如下图:
现在加密密钥为,如上所示,明文“6”通过加密后得到密文“3”,再发送,接受方通过解密密钥解密得到明文“6”.问:若接受方接到密文为“4”,则解密后得明文为 .
16、从中,得出的一般性结论是 .
答案卷
一选择(请将你所选的答案填入下表)
序号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二填空:(请将填空题答案分别填入对应的题空中)
1, 。 2,
3, 4,
三,解答题
17.(12分)已知函数,求的最大值.
18、(12分)直线分抛物线与轴所围成图形为面积相等的两个部分,求的值.
19、(12分)设0 < a, b, c < 1,求证:(1 a)b, (1 b)c, (1 c)a,不可能同时大于
20.(12分) (本题12分)水库的蓄水量随时间而变化,现用表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于的近似函数关系式为:
(1)该水库的蓄求量小于50的时期称为枯水期.以表示第i月份(),同一年内哪几个月份是枯水期?
(2)求一年内该水库的最大蓄水量(取计算).
21.(12分)(本题12分)已知数列,,,…,,…,
(1)计算S1,S2,S3,S4,(2)根据计算结果,猜想Sn的表达式,并用数学归纳法进行证明.
22、(14分)已知函数其中n∈N*,a为常数.(Ⅰ)当n=2时,求函数f(x)的极值;(Ⅱ)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
参考答案
一、选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7
答案 C C D D
题号 8 9 10 11 12 13 14
答案 D B D C B
二、填空题(每小题4分,共16分)
13 14. 2
15. 14 16 n+(n+1)+(n+2)+…+(3n-2)=(2n-1)
.三、解答题
17.用求导的方法可求得的最大值为0
18.解方程组 得:直线分抛物线的交点的横坐标为
和抛物线与轴所围成图形为面积为
由题设得
又,
所以,从而得:
19证:设(1 a)b >, (1 b)c >, (1 c)a >,
则三式相乘:ab < (1 a)b (1 b)c (1 c)a < ①
又∵0 < a, b, c < 1 ∴
同理:,
以上三式相乘: (1 a)a (1 b)b (1 c)c≤ 与①矛盾 ∴原式成立
20.解:(1)①当时,化简得,
解得.
②当时,,化简得
解得.
综上得,,或.故知枯水期为1月,2月,3月,4月,11月,12月共6个月。
(2)由(1)知,的最大值只能在(4,10)内达到。
由,
令,解得(舍去)。
在时取得最大值(亿立方米)。
故知一年内该水库的最大蓄水量是108.32亿立方米。
21: S1==;S2=+=;S3=+=;S4=+=.
可以看到,上面表示四个结果的分数中,分子与项数n一致,分母可用项数n表示为3n+1.
于是可以猜想.
下面我们用数学归纳法证明这个猜想.
(1)当n=1时,左边=S1=, 右边===, 猜想成立.
(2)假设当n=k(k∈N*)时猜想成立,即
+++…+=,
那么, +++…++
所以,当n=k+1时猜想也成立.
根据(1)、(2),可知猜想对任何n∈N*都成立.
22.(I)的定义域为,当时当时,由得当时,单调递减;当时,单调递增。纵上可知时,当时在处取得极小值为
(II)当时,
当时,对任意恒有,故只需证。令,,
故在上单调递增,即在上恒成立,而恒成立,因此,当时,恒有
x
y
O
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
解密密钥密码
加密密钥密码
明文
密文
密文
发送
明文
一、选择题:(每题5分共60分,每题有且仅有一个正确答案)
1、曲线在点处的切线方程为( )
A. B. C. D.
2.设,则( )
A. B.
C. D.
3.由抛物线与直线所围成的图形的面积是( ).
A. B.38/3 C.16/3 D.
4、5.函数的单调递减区间是( )
A.(,+∞) B.(-∞,) C.(0,) D.(e,+∞)
5.下面使用类比推理正确的是 ( )
A.“若,则”类推出“若,则”
B.“若”类推出“”
C.“若” 类推出“ (c≠0)”
D.“” 类推出“”
6.设是定义在整数集上的函数,且满足:“当成立时,总可以推出成立”。那么下列命题总成立的是( )
A.若成立,则当时均有成立
B.若成立,则当时均有成立
C.若成立,则当时均有成立
D.若成立,则当时均有成立
7.设, ,n∈N,则
( )
A. B.- C. D.-
8.如果10N的力能使弹簧压缩10cm,为在弹性限度内将弹簧拉长6cm,则力所做的功为( )
A.0.28J B.0.12J C.0.26J D.0.18J
9.已知 ,猜想的表达式为 ( )
A. B. C. D.
10..设函数f(x)在定义域内可导,y=f(x)的图象如下右图所示,则导函数y=f (x)可能为( )
11.对于R上可导的任意函数f(x),且若满足(x-1)>0,则必有( )
A.f(0)+f(2)2f(1) B.f(0)+f(2)2f(1)
C.f(0)+f(2)>2f(1) D.f(0)+f(2)2f(1)
12、把下面在平面内成立的结论类比地推广到空间,结论还正确的是( )
(A) 如果一条直线与两条平行线中的一条相交,则它与另一条相交 .
(B) 如果一条直线与两条平行线中的一条垂直,则它与另一条垂直.
(C) 如果两条直线同时与第三条直线相交,则这两条直线相交.
(D) 如果两条直线同时与第三条直线垂直,则这两条直线平行.
二、填空题(每题4分共16分)
13、设函数f(x)=ax2+c(a≠0).若,0≤x0≤1,则x0的值为_____
14. 已知f(n)==
15、、为了保证信息安全传输,有一种称为秘密密钥密码系统(Private Key Cryptosystem),其加密、解密原理如下图:
现在加密密钥为,如上所示,明文“6”通过加密后得到密文“3”,再发送,接受方通过解密密钥解密得到明文“6”.问:若接受方接到密文为“4”,则解密后得明文为 .
16、从中,得出的一般性结论是 .
答案卷
一选择(请将你所选的答案填入下表)
序号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二填空:(请将填空题答案分别填入对应的题空中)
1, 。 2,
3, 4,
三,解答题
17.(12分)已知函数,求的最大值.
18、(12分)直线分抛物线与轴所围成图形为面积相等的两个部分,求的值.
19、(12分)设0 < a, b, c < 1,求证:(1 a)b, (1 b)c, (1 c)a,不可能同时大于
20.(12分) (本题12分)水库的蓄水量随时间而变化,现用表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于的近似函数关系式为:
(1)该水库的蓄求量小于50的时期称为枯水期.以表示第i月份(),同一年内哪几个月份是枯水期?
(2)求一年内该水库的最大蓄水量(取计算).
21.(12分)(本题12分)已知数列,,,…,,…,
(1)计算S1,S2,S3,S4,(2)根据计算结果,猜想Sn的表达式,并用数学归纳法进行证明.
22、(14分)已知函数其中n∈N*,a为常数.(Ⅰ)当n=2时,求函数f(x)的极值;(Ⅱ)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
参考答案
一、选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7
答案 C C D D
题号 8 9 10 11 12 13 14
答案 D B D C B
二、填空题(每小题4分,共16分)
13 14. 2
15. 14 16 n+(n+1)+(n+2)+…+(3n-2)=(2n-1)
.三、解答题
17.用求导的方法可求得的最大值为0
18.解方程组 得:直线分抛物线的交点的横坐标为
和抛物线与轴所围成图形为面积为
由题设得
又,
所以,从而得:
19证:设(1 a)b >, (1 b)c >, (1 c)a >,
则三式相乘:ab < (1 a)b (1 b)c (1 c)a < ①
又∵0 < a, b, c < 1 ∴
同理:,
以上三式相乘: (1 a)a (1 b)b (1 c)c≤ 与①矛盾 ∴原式成立
20.解:(1)①当时,化简得,
解得.
②当时,,化简得
解得.
综上得,,或.故知枯水期为1月,2月,3月,4月,11月,12月共6个月。
(2)由(1)知,的最大值只能在(4,10)内达到。
由,
令,解得(舍去)。
在时取得最大值(亿立方米)。
故知一年内该水库的最大蓄水量是108.32亿立方米。
21: S1==;S2=+=;S3=+=;S4=+=.
可以看到,上面表示四个结果的分数中,分子与项数n一致,分母可用项数n表示为3n+1.
于是可以猜想.
下面我们用数学归纳法证明这个猜想.
(1)当n=1时,左边=S1=, 右边===, 猜想成立.
(2)假设当n=k(k∈N*)时猜想成立,即
+++…+=,
那么, +++…++
所以,当n=k+1时猜想也成立.
根据(1)、(2),可知猜想对任何n∈N*都成立.
22.(I)的定义域为,当时当时,由得当时,单调递减;当时,单调递增。纵上可知时,当时在处取得极小值为
(II)当时,
当时,对任意恒有,故只需证。令,,
故在上单调递增,即在上恒成立,而恒成立,因此,当时,恒有
x
y
O
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
解密密钥密码
加密密钥密码
明文
密文
密文
发送
明文
