鲁教版(五四制)数学六年级上册 认识幻方并探寻其简单的数量关系 教案
文档属性
| 名称 | 鲁教版(五四制)数学六年级上册 认识幻方并探寻其简单的数量关系 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 38.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 20:37:56 | ||
图片预览

文档简介
综合与实践:探寻神奇的幻方
教材分析:
综合与实践是指一类以问题为载体,以学生自主参与为主的学习活动,可以理解为“数学探究”和“数学建模或数学实际应用”。本课时以探寻三阶幻方的本质特征为载体,提高学生综合运用有理数运算、整式的加减、探索规律、方程的能力,感受图形的对称,体验数形结合的思想.
教学时教师要提供学生充足探索数量关系并符号化的时间,培养学生言之有据的习惯,发展学生正确使用数学语言进行表达和交流的能力,同时要鼓励学生在探索的过程中多角度尝试.
教学目标:
1.借助字母表示数、探索规律揭示几种简单的三阶幻方的本质特征;体验有理数混合运算、字母表示数、探索规律与几种三阶幻方本质特征的内在联系;能够快速对含有具体数字的不完整幻方进行补充,掌握幻方的形成和相等关系的一般性描述.
2.经历观察、猜想、验证、归纳、类比等活动, 初步积累构造三阶幻方的经验,建立数感、符号意识发展抽象思维,体会由特殊到一般的数学思想方法,在合作交流、自主探究中感悟数学的思维方式.
3.借助洛书、杨辉幻方等史料,帮助学生感受祖国文化的博大精深,增强民族自豪感,激发他们将民族瑰宝进一步发扬光大的信心和决心,从幻方对称的图形、美妙的结论中,初步感受数学的美.
学情分析:
学生此前已完成“有理数及其运算” “整式及其加减”与“一元一次方程”的学习,部分学生对用1~9填成三阶幻方,在方法上有初步的感性认识,但可能仅限于此,并未进行深入研究.
学生通过本“综合实践”课,在问题串引导下综合运用知识解决问题,对解决问题的方法和经验进行反思,从中感受一种全新的以自主探究为特色的学习方式,提高学习数学的兴趣、信心和能力,改变学习方式,加深对数学本质的认识.
教学重点:探索三阶幻方的本质特征
教学难点:构造符合要求的三阶幻方
教学用具:PPT,幻方卡片、学案
教学过程:
课前准备:
1.将1——9九个数字填写在3×3的方格中,使得每个横行、每个竖列和每条对角线上的三个数之和都相等。
2.查阅与幻方有关的资料,了解世界上最早的幻方。
【设计意图】课前安排学生通过上网等方式查阅资料,了解幻方的有关知识,使学生对幻方有更深入、更全面的了解,对所学的知识产生兴趣。自己尝试构建基础三阶幻方,初步感知幻方的特点。
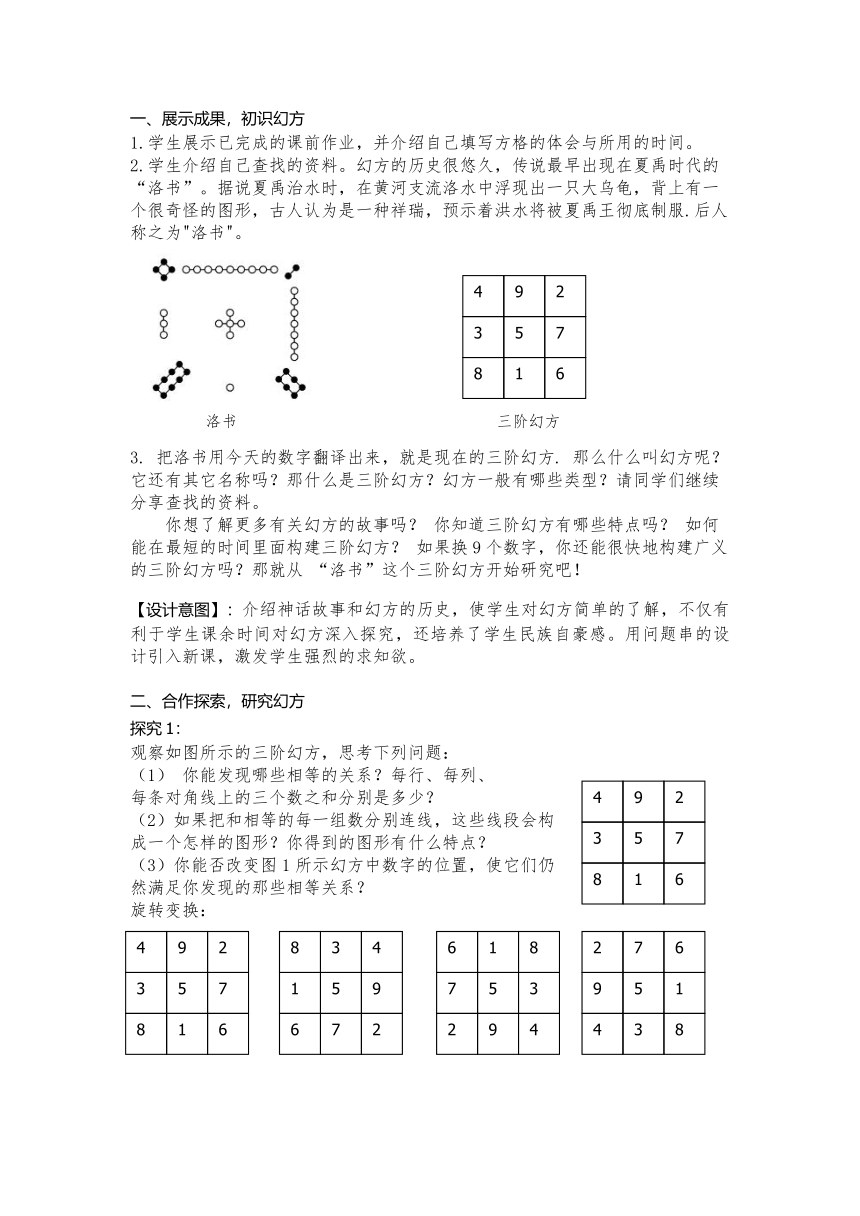
一、展示成果,初识幻方
1.学生展示已完成的课前作业,并介绍自己填写方格的体会与所用的时间。
2.学生介绍自己查找的资料。幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”。据说夏禹治水时,在黄河支流洛水中浮现出一只大乌龟,背上有一个很奇怪的图形,古人认为是一种祥瑞,预示着洪水将被夏禹王彻底制服.后人称之为"洛书"。
(
2
9
4
3
5
7
8
1
6
)
(
三阶幻方
) (
洛书
)
3. 把洛书用今天的数字翻译出来,就是现在的三阶幻方. 那么什么叫幻方呢?它还有其它名称吗?那什么是三阶幻方?幻方一般有哪些类型?请同学们继续分享查找的资料。
你想了解更多有关幻方的故事吗? 你知道三阶幻方有哪些特点吗? 如何能在最短的时间里面构建三阶幻方? 如果换9个数字,你还能很快地构建广义的三阶幻方吗?那就从 “洛书”这个三阶幻方开始研究吧!
【设计意图】:介绍神话故事和幻方的历史,使学生对幻方简单的了解,不仅有利于学生课余时间对幻方深入探究,还培养了学生民族自豪感。用问题串的设计引入新课,激发学生强烈的求知欲。
二、合作探索,研究幻方
探究1:
观察如图所示的三阶幻方,思考下列问题:
(
2
9
4
3
5
7
8
1
6
)你能发现哪些相等的关系?每行、每列、
每条对角线上的三个数之和分别是多少?
(2)如果把和相等的每一组数分别连线,这些线段会构成一个怎样的图形?你得到的图形有什么特点?
(3)你能否改变图1所示幻方中数字的位置,使它们仍然满足你发现的那些相等关系?
旋转变换:
(
2
9
4
3
5
7
8
1
6
4
3
8
1
5
9
6
7
2
8
1
6
7
5
3
2
9
4
6
7
2
9
5
1
4
3
8
)
对称变换:
(
8
3
4
9
5
1
2
7
6
) (
2
7
6
1
5
9
8
3
4
) (
4
9
2
7
5
3
6
1
8
) (
6
1
8
3
5
7
4
9
2
)
三阶幻方共有8个,相互之间可以由对称或者旋转得到.
(4)在你构造的幻方中,最核心的位置是什么?在这个位置上出现的数是几?有没有“成对”出现的数?
如图,将九个数字分别用a,b,c,d,e,f,g,h,i来表示,因为1-9个数的和为45,所以每行、每列、每条对角线上的三个数之和都是15,即:
(
c
b
a
d
e
f
g
h
i
)a+e+f=15,c+e+g=15 ,b+e+h=15,三式相加得(a+b+c+i+g+h)+3e=45,因此,e=5
(5)在如图所示三阶幻方中,中心方格中的数5与每行、每列和每条对角线上的三个数之和之间有什么关系?
结论1: 三阶幻方的幻和=中间数×3;
结论2:“成对”数的和=中间数×2;
结论3:角上的数字×2=与之不相邻的两个边块数字的和。
(6)你还有什么新的发现?
方法1:奇偶试验法
方法2:成对试验法
奇数 偶数 奇数
偶数 5 偶数
奇数 偶数 奇数
偶数 奇数 偶数
奇数 5 奇数
偶数 奇数 偶数
(
2
9
4
3
5
7
8
1
6
)
(
(×)
)
【设计意图】问题1、2分别从数与形的角度对三阶幻方进行观察;问题3从变化的角度研究幻方,让学生在变与不变中感受幻方的幻之所在;问题4让学生从感性与理性的双重角度理解中间位置的特殊性,成对数据的必要性;问题5让学生明确幻方中数据之间的结论;问题6给学生开放的空间,通过自由探索得出新的结论。在这一探究活动,有独立思考、小组讨论、合作探究等多种形式穿插进行,让学生基本都能掌握三阶幻方的特点。
三、学以致用,制作幻方
(
-5
-6
-11
) (
-1
4
3
)探究2:在图中所示广义的三阶幻方中分别给出了3个数,你能将其余六上数全填上吗?
【设计意图】初步应用结论填写方格,从数的角度感受数学的对称美,在应用的过程中体会成功探索结论的喜悦,并且形成填写幻方的经验。
探究3:
(1)用2、3、4、5、6、7、8、9、10这九个数如何构造一个广义的三阶幻方?
(2) 用2、4、6、8、10、12、14、16、18这九个数如何构造一个广义的三阶幻方?
(3)用-8、-6、-4、-2、0、2、4、6、8这九个数如何构造一个广义的三阶幻方?
(
图(
1
)
图(
2
)
图(
3
)
备用图
)
(4)说一说,你是用什么方法制作幻方的?
【设计意图】设置多角度的实践机会,对幻方进行拓展变式,帮助每个学生在实践中形成对三阶幻方的感性认识,促使更多学生将感性认识上升到理性结论,并将自己的经验形成方法。
四、梳理小结,共谈体会
请从下列关键词中选出一个或是几个,谈一谈你对这节课的收获与感受。
我了解了 我学会了 我掌握了 我欣赏 我希望 …… 知识 方法 题型 某某同学 自己 ……
【设计意图】学生根据关键词索引进行知识梳理与课堂小结,能够全方位地感知课堂,既有对知识、方法、题型的关注,更有对自己学习过程感受的评价,也有对同学表现的认可,在帮助学生形成知识体系的同时,渗透小结方法,加深同学之间的情谊,更好的促进学生数学学习。
五、课后作业,拓展延伸
1.(必做题)在下列各图的空格里,填上合适的数,使横行、竖列及两条对角线上三个数的和都相等.
日 一 二 三 四 五 六
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30
(
8
4
2
) (
9
2
10
)
(
第
1
题图(
2
)
) (
第
1
题图(
1
)()
) (
第
2
题图
)
2.(必做题)利用一个3×3的方框在日历图上任意套出9个数,这9个数能否构造一个广义的三阶幻方?为什么?
3.(选做题)自行选取一组数构造一个三阶幻方,使得每行、每列和每条对角线上的三个数之和都等于60.
(
备用图
) (
第3题图
)
【设计意图】:分层次作业的设置,为学生搭建不同高度的学习平台,满足不同层次学生学习数学的需要,鼓励学有余力的学生课外自主探究。
六、板书设计
电脑屏幕 展开与折叠 1.幻方的概念、分类 2.探索的结论 ① ② ③ ④ 预习展示区 方法总结区
教材分析:
综合与实践是指一类以问题为载体,以学生自主参与为主的学习活动,可以理解为“数学探究”和“数学建模或数学实际应用”。本课时以探寻三阶幻方的本质特征为载体,提高学生综合运用有理数运算、整式的加减、探索规律、方程的能力,感受图形的对称,体验数形结合的思想.
教学时教师要提供学生充足探索数量关系并符号化的时间,培养学生言之有据的习惯,发展学生正确使用数学语言进行表达和交流的能力,同时要鼓励学生在探索的过程中多角度尝试.
教学目标:
1.借助字母表示数、探索规律揭示几种简单的三阶幻方的本质特征;体验有理数混合运算、字母表示数、探索规律与几种三阶幻方本质特征的内在联系;能够快速对含有具体数字的不完整幻方进行补充,掌握幻方的形成和相等关系的一般性描述.
2.经历观察、猜想、验证、归纳、类比等活动, 初步积累构造三阶幻方的经验,建立数感、符号意识发展抽象思维,体会由特殊到一般的数学思想方法,在合作交流、自主探究中感悟数学的思维方式.
3.借助洛书、杨辉幻方等史料,帮助学生感受祖国文化的博大精深,增强民族自豪感,激发他们将民族瑰宝进一步发扬光大的信心和决心,从幻方对称的图形、美妙的结论中,初步感受数学的美.
学情分析:
学生此前已完成“有理数及其运算” “整式及其加减”与“一元一次方程”的学习,部分学生对用1~9填成三阶幻方,在方法上有初步的感性认识,但可能仅限于此,并未进行深入研究.
学生通过本“综合实践”课,在问题串引导下综合运用知识解决问题,对解决问题的方法和经验进行反思,从中感受一种全新的以自主探究为特色的学习方式,提高学习数学的兴趣、信心和能力,改变学习方式,加深对数学本质的认识.
教学重点:探索三阶幻方的本质特征
教学难点:构造符合要求的三阶幻方
教学用具:PPT,幻方卡片、学案
教学过程:
课前准备:
1.将1——9九个数字填写在3×3的方格中,使得每个横行、每个竖列和每条对角线上的三个数之和都相等。
2.查阅与幻方有关的资料,了解世界上最早的幻方。
【设计意图】课前安排学生通过上网等方式查阅资料,了解幻方的有关知识,使学生对幻方有更深入、更全面的了解,对所学的知识产生兴趣。自己尝试构建基础三阶幻方,初步感知幻方的特点。
一、展示成果,初识幻方
1.学生展示已完成的课前作业,并介绍自己填写方格的体会与所用的时间。
2.学生介绍自己查找的资料。幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”。据说夏禹治水时,在黄河支流洛水中浮现出一只大乌龟,背上有一个很奇怪的图形,古人认为是一种祥瑞,预示着洪水将被夏禹王彻底制服.后人称之为"洛书"。
(
2
9
4
3
5
7
8
1
6
)
(
三阶幻方
) (
洛书
)
3. 把洛书用今天的数字翻译出来,就是现在的三阶幻方. 那么什么叫幻方呢?它还有其它名称吗?那什么是三阶幻方?幻方一般有哪些类型?请同学们继续分享查找的资料。
你想了解更多有关幻方的故事吗? 你知道三阶幻方有哪些特点吗? 如何能在最短的时间里面构建三阶幻方? 如果换9个数字,你还能很快地构建广义的三阶幻方吗?那就从 “洛书”这个三阶幻方开始研究吧!
【设计意图】:介绍神话故事和幻方的历史,使学生对幻方简单的了解,不仅有利于学生课余时间对幻方深入探究,还培养了学生民族自豪感。用问题串的设计引入新课,激发学生强烈的求知欲。
二、合作探索,研究幻方
探究1:
观察如图所示的三阶幻方,思考下列问题:
(
2
9
4
3
5
7
8
1
6
)你能发现哪些相等的关系?每行、每列、
每条对角线上的三个数之和分别是多少?
(2)如果把和相等的每一组数分别连线,这些线段会构成一个怎样的图形?你得到的图形有什么特点?
(3)你能否改变图1所示幻方中数字的位置,使它们仍然满足你发现的那些相等关系?
旋转变换:
(
2
9
4
3
5
7
8
1
6
4
3
8
1
5
9
6
7
2
8
1
6
7
5
3
2
9
4
6
7
2
9
5
1
4
3
8
)
对称变换:
(
8
3
4
9
5
1
2
7
6
) (
2
7
6
1
5
9
8
3
4
) (
4
9
2
7
5
3
6
1
8
) (
6
1
8
3
5
7
4
9
2
)
三阶幻方共有8个,相互之间可以由对称或者旋转得到.
(4)在你构造的幻方中,最核心的位置是什么?在这个位置上出现的数是几?有没有“成对”出现的数?
如图,将九个数字分别用a,b,c,d,e,f,g,h,i来表示,因为1-9个数的和为45,所以每行、每列、每条对角线上的三个数之和都是15,即:
(
c
b
a
d
e
f
g
h
i
)a+e+f=15,c+e+g=15 ,b+e+h=15,三式相加得(a+b+c+i+g+h)+3e=45,因此,e=5
(5)在如图所示三阶幻方中,中心方格中的数5与每行、每列和每条对角线上的三个数之和之间有什么关系?
结论1: 三阶幻方的幻和=中间数×3;
结论2:“成对”数的和=中间数×2;
结论3:角上的数字×2=与之不相邻的两个边块数字的和。
(6)你还有什么新的发现?
方法1:奇偶试验法
方法2:成对试验法
奇数 偶数 奇数
偶数 5 偶数
奇数 偶数 奇数
偶数 奇数 偶数
奇数 5 奇数
偶数 奇数 偶数
(
2
9
4
3
5
7
8
1
6
)
(
(×)
)
【设计意图】问题1、2分别从数与形的角度对三阶幻方进行观察;问题3从变化的角度研究幻方,让学生在变与不变中感受幻方的幻之所在;问题4让学生从感性与理性的双重角度理解中间位置的特殊性,成对数据的必要性;问题5让学生明确幻方中数据之间的结论;问题6给学生开放的空间,通过自由探索得出新的结论。在这一探究活动,有独立思考、小组讨论、合作探究等多种形式穿插进行,让学生基本都能掌握三阶幻方的特点。
三、学以致用,制作幻方
(
-5
-6
-11
) (
-1
4
3
)探究2:在图中所示广义的三阶幻方中分别给出了3个数,你能将其余六上数全填上吗?
【设计意图】初步应用结论填写方格,从数的角度感受数学的对称美,在应用的过程中体会成功探索结论的喜悦,并且形成填写幻方的经验。
探究3:
(1)用2、3、4、5、6、7、8、9、10这九个数如何构造一个广义的三阶幻方?
(2) 用2、4、6、8、10、12、14、16、18这九个数如何构造一个广义的三阶幻方?
(3)用-8、-6、-4、-2、0、2、4、6、8这九个数如何构造一个广义的三阶幻方?
(
图(
1
)
图(
2
)
图(
3
)
备用图
)
(4)说一说,你是用什么方法制作幻方的?
【设计意图】设置多角度的实践机会,对幻方进行拓展变式,帮助每个学生在实践中形成对三阶幻方的感性认识,促使更多学生将感性认识上升到理性结论,并将自己的经验形成方法。
四、梳理小结,共谈体会
请从下列关键词中选出一个或是几个,谈一谈你对这节课的收获与感受。
我了解了 我学会了 我掌握了 我欣赏 我希望 …… 知识 方法 题型 某某同学 自己 ……
【设计意图】学生根据关键词索引进行知识梳理与课堂小结,能够全方位地感知课堂,既有对知识、方法、题型的关注,更有对自己学习过程感受的评价,也有对同学表现的认可,在帮助学生形成知识体系的同时,渗透小结方法,加深同学之间的情谊,更好的促进学生数学学习。
五、课后作业,拓展延伸
1.(必做题)在下列各图的空格里,填上合适的数,使横行、竖列及两条对角线上三个数的和都相等.
日 一 二 三 四 五 六
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30
(
8
4
2
) (
9
2
10
)
(
第
1
题图(
2
)
) (
第
1
题图(
1
)()
) (
第
2
题图
)
2.(必做题)利用一个3×3的方框在日历图上任意套出9个数,这9个数能否构造一个广义的三阶幻方?为什么?
3.(选做题)自行选取一组数构造一个三阶幻方,使得每行、每列和每条对角线上的三个数之和都等于60.
(
备用图
) (
第3题图
)
【设计意图】:分层次作业的设置,为学生搭建不同高度的学习平台,满足不同层次学生学习数学的需要,鼓励学有余力的学生课外自主探究。
六、板书设计
电脑屏幕 展开与折叠 1.幻方的概念、分类 2.探索的结论 ① ② ③ ④ 预习展示区 方法总结区
