鲁教版(五四制)数学六年级上册 3.7 .1探索规律课件(共13张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学六年级上册 3.7 .1探索规律课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 122.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 19:49:31 | ||
图片预览


文档简介
(共13张PPT)
第一课时
探索规律
1.经历由特殊到一般和由一般到特殊的过程,体会代数式推理的特点和作用。
2.能用代数式表示并借助代数式运算验证所探索规律的一般性。
学习目标
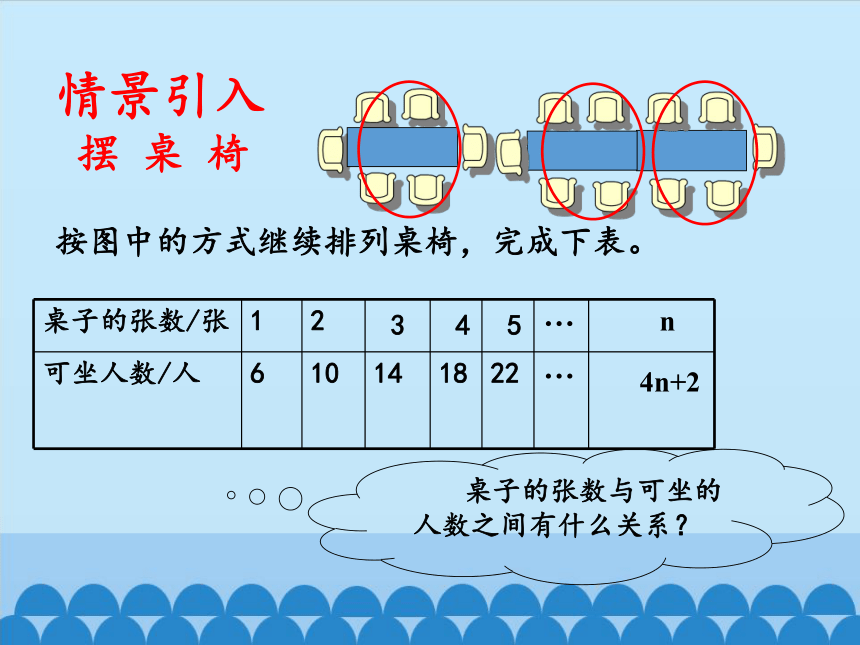
按图中的方式继续排列桌椅,完成下表。
桌子的张数/张 1 2 3 4 5 …
可坐人数/人 6 10 14 18 22 …
情景引入
摆 桌 椅
桌子的张数与可坐的人数之间有什么关系?
n
4n+2
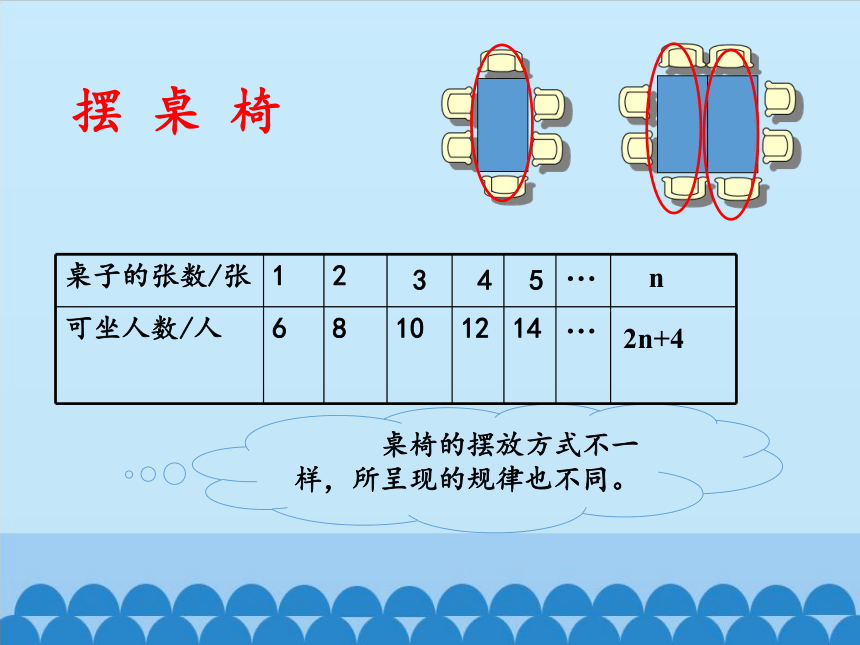
桌椅的摆放方式不一样,所呈现的规律也不同。
摆 桌 椅
桌子的张数/张 1 2 3 4 5 …
可坐人数/人 6 8 10 12 14 …
n
2n+4
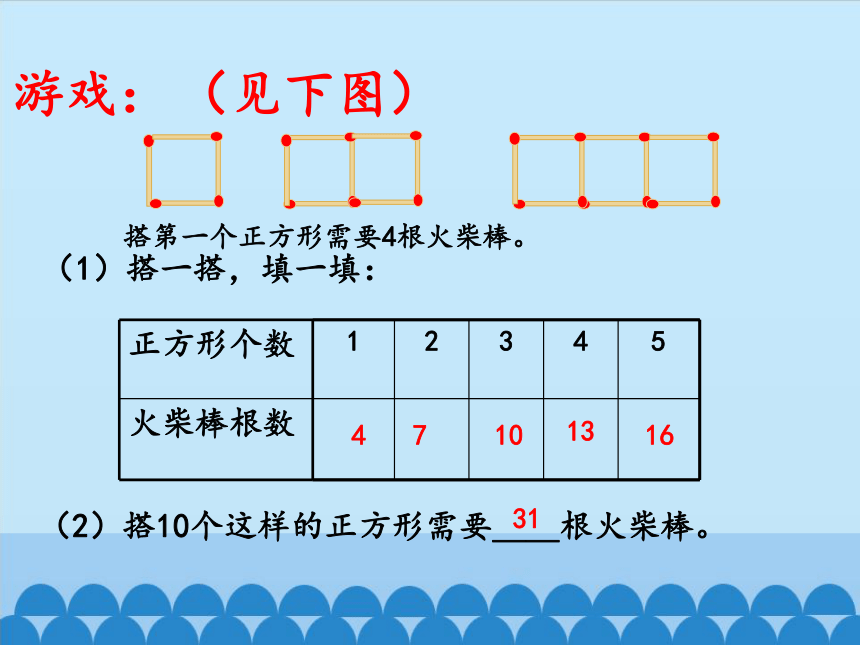
游戏: (见下图)
搭第一个正方形需要4根火柴棒。
(1)搭一搭,填一填:
正方形个数
火柴棒根数 1 2 3 4 5
4
7
10
13
16
(2)搭10个这样的正方形需要__根火柴棒。
31
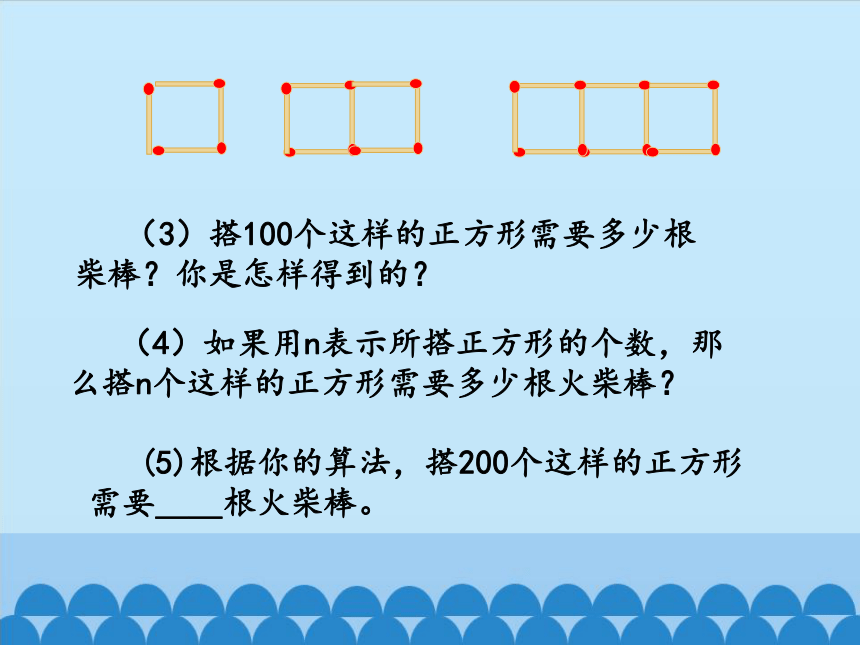
(4)如果用n表示所搭正方形的个数,那么搭n个这样的正方形需要多少根火柴棒?
(5)根据你的算法,搭200个这样的正方形需要__根火柴棒。
(3)搭100个这样的正方形需要多少根柴棒?你是怎样得到的?
4+3(n-1)
(用火柴棒拼n个正方形)
……
(n-1)个
探索规律(方法1)
n+n+(n+1)
(用火柴棒拼n个正方形)
……
n根
n根
探索规律(方法2)
探索规律(方法3)
(用火柴棒拼n个正方形)
1+3n
……
n个
4n-(n-1)
(用火柴棒拼n个正方形)
探索规律(方法4)
……
n个
(n-1)个
创造活动:
1.新都快餐厅改扩建后,要在新餐厅摆放一批前图中所示的桌椅,餐厅为正方形,要安排40人同时就餐,请设计一种桌椅摆放方案,要求没有剩余桌椅(要求选用前图中的摆放方式),请画出你满意的设计图。
2.一批小球按下面的方法堆放
你知道第n堆有多少个小球吗?
(1+n) ×n ÷2
第5堆有( )个小球,
第8堆有( )个小球。
15
36
谢 谢
第一课时
探索规律
1.经历由特殊到一般和由一般到特殊的过程,体会代数式推理的特点和作用。
2.能用代数式表示并借助代数式运算验证所探索规律的一般性。
学习目标
按图中的方式继续排列桌椅,完成下表。
桌子的张数/张 1 2 3 4 5 …
可坐人数/人 6 10 14 18 22 …
情景引入
摆 桌 椅
桌子的张数与可坐的人数之间有什么关系?
n
4n+2
桌椅的摆放方式不一样,所呈现的规律也不同。
摆 桌 椅
桌子的张数/张 1 2 3 4 5 …
可坐人数/人 6 8 10 12 14 …
n
2n+4
游戏: (见下图)
搭第一个正方形需要4根火柴棒。
(1)搭一搭,填一填:
正方形个数
火柴棒根数 1 2 3 4 5
4
7
10
13
16
(2)搭10个这样的正方形需要__根火柴棒。
31
(4)如果用n表示所搭正方形的个数,那么搭n个这样的正方形需要多少根火柴棒?
(5)根据你的算法,搭200个这样的正方形需要__根火柴棒。
(3)搭100个这样的正方形需要多少根柴棒?你是怎样得到的?
4+3(n-1)
(用火柴棒拼n个正方形)
……
(n-1)个
探索规律(方法1)
n+n+(n+1)
(用火柴棒拼n个正方形)
……
n根
n根
探索规律(方法2)
探索规律(方法3)
(用火柴棒拼n个正方形)
1+3n
……
n个
4n-(n-1)
(用火柴棒拼n个正方形)
探索规律(方法4)
……
n个
(n-1)个
创造活动:
1.新都快餐厅改扩建后,要在新餐厅摆放一批前图中所示的桌椅,餐厅为正方形,要安排40人同时就餐,请设计一种桌椅摆放方案,要求没有剩余桌椅(要求选用前图中的摆放方式),请画出你满意的设计图。
2.一批小球按下面的方法堆放
你知道第n堆有多少个小球吗?
(1+n) ×n ÷2
第5堆有( )个小球,
第8堆有( )个小球。
15
36
谢 谢
