2021-2022学年安徽省宣城市三县四校教学联盟九年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年安徽省宣城市三县四校教学联盟九年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 636.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 10:52:53 | ||
图片预览




文档简介
2021-2022学年安徽省宣城市三县四校教学联盟九年级(上)期中数学试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)在下面的图形中,相似的一组是( )
A.
B.
C.
D.
2.(4分)抛物线的解析式y=﹣2x2+1,则顶点坐标是( )
A.(﹣2,1) B.(0,1) C.(﹣2,﹣1) D.(0,﹣1)
3.(4分)若,则的值为( )
A. B.﹣ C. D.
4.(4分)下列各点中,在反比例函数y=﹣图象上的是( )
A.(﹣1,4) B.(1,4) C.(﹣2,﹣2) D.(2,2)
5.(4分)某商场降价销售一批名牌球鞋,已知所获利润y(元)与降价金额x(元)之间满定函数关系式y=﹣x2+50x+600,若降价10元,则获利为( )
A.800元 B.600元 C.1200元 D.1000元
6.(4分)若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=4m,BC=5cm,则矩形EFGH的周长是( )
A.12cm B.27cm C.24cm D.18cm
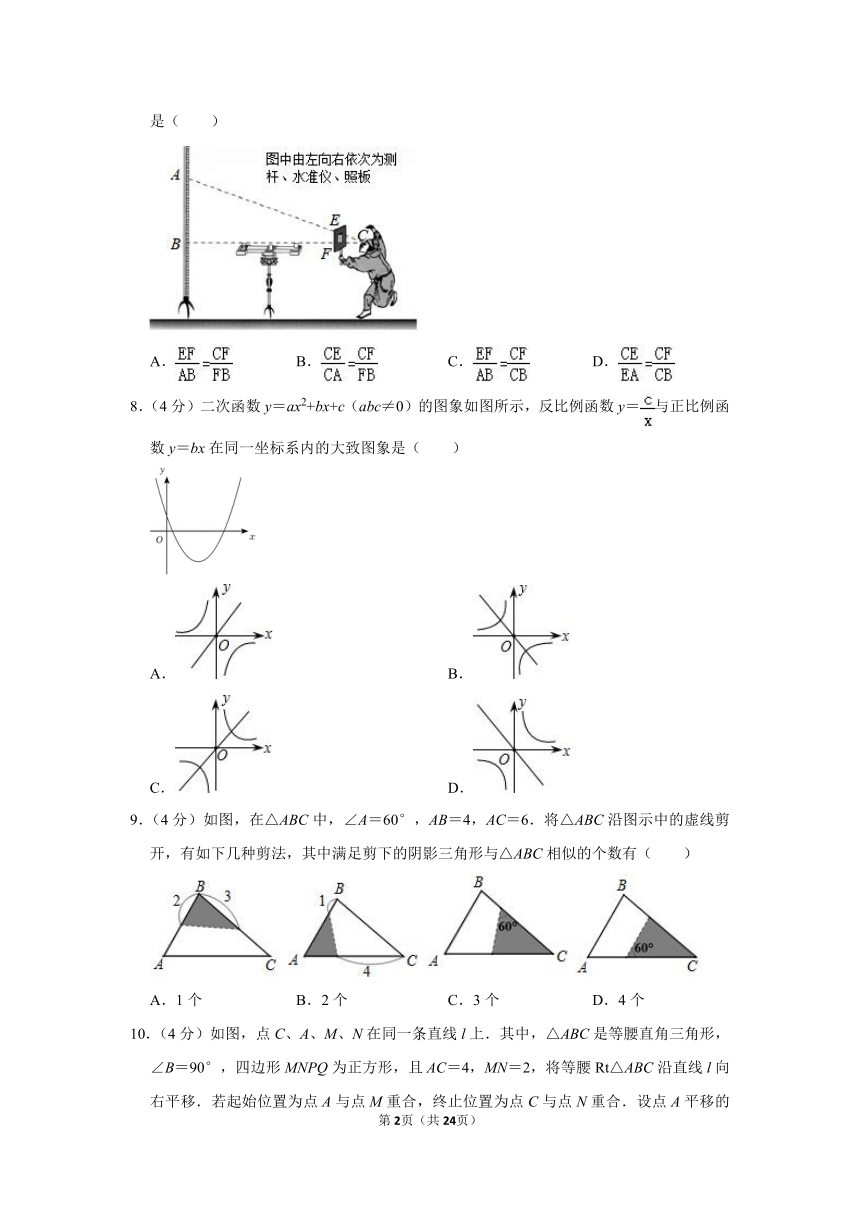
7.(4分)“计里画方”(比例缩放和直角坐标网格体系)是中国古代地图制图的基本方法和数学基础,是中国古代地图独立发展的重要标志.制作地图时,人们会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
8.(4分)二次函数y=ax2+bx+c(abc≠0)的图象如图所示,反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象是( )
A. B.
C. D.
9.(4分)如图,在△ABC中,∠A=60°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,有如下几种剪法,其中满足剪下的阴影三角形与△ABC相似的个数有( )
A.1个 B.2个 C.3个 D.4个
10.(4分)如图,点C、A、M、N在同一条直线l上.其中,△ABC是等腰直角三角形,∠B=90°,四边形MNPQ为正方形,且AC=4,MN=2,将等腰Rt△ABC沿直线l向右平移.若起始位置为点A与点M重合,终止位置为点C与点N重合.设点A平移的距离为x,两个图形重叠部分的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)二次函数y=(3﹣x)2图象的开口向 .
12.(5分)如果两个相似多边形面积的比为25:49,则它们的相似比为 .
13.(5分)如图,已知一次函数y=ax(a<0)与反比例函数y=(x<0)的图象相交于点A,过点A作AB⊥y轴,垂足为B,若△OAB的面积为4,则k的值为 .
14.(5分)如图,在平行四边形ABCD中,AC,BD相交于点O,E是OA的中点,连接BE并延长交AD于点F.
(1)= .
(2)若△AEF的面积为4,则平行四边形ABCD的面积为 .
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知二次函数y=x2﹣2x﹣1,在平面直角坐标系中画出它的图象,并写出它的顶点坐标.
16.(8分)已知反比例函数y=的图象经过点A(3,﹣2).
(1)求k的值.
(2)点A(x1,y1),B(x2,y2)均在反比例函数y=的图象上,若0<x1<x2,直接写出y1,y2的大小关系.
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)如图,在△ABC中,点D、E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G.
(1)求证:△AED∽△ABC.
(2)若AG平分∠BAC,求证:.
18.(8分)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象分别交x轴,y轴于A,B两点,与反比例函数y=(k≠0)的图象交于C,D两点,DE⊥x轴于点E,点C的坐标为(6,﹣1),DE=3.
(1)求反比例函数与一次函数的表达式;
(2)求△COD的面积.
五、(本大题共2小题,每小题10分;满分20分)
19.(10分)如图,在四边形ABCD中,AD∥BC,∠BAD=90°,且BD⊥DC.
(1)△ABD与△DCB相似吗?请说明理由;
(2)若AD=4,BC=9,请求出BD的长.
20.(10分)如图,抛物线y=ax2+bx+4(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,求△PAC周长的最小值.
六、(本题满分12分)
21.(12分)某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,放置一个平面镜E来测量学校旗杆的高度,当镜子中心与旗杆的距离EB=20米,镜子中心与测量者的距离ED=2米时,测量者刚好从镜子中看到旗杆的顶端点A.已知测量者的身高为1.6米,测量者的眼睛距地面的高度为1.5米,求学校旗杆的高度是多少米.
(1)在计算过程中C,D之间的距离应是 米.
(2)根据以上测量结果,请你帮助“综合与实践”小组求出学校旗杆AB的高度.
(3)该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)
七、(本题满分12分)
22.(12分)某地种植某种水果,其成本经过测算为20元/kg,投放市场后,经过市场调研发现,这种水果在上市的一段时间内的销售单价p(元/kg)与时间t(天)之间的函数图象如图所示,且其日销售量y(kg)与时间t(天)的关系是y=﹣2t+120,天数为整数.
(1)试求销售单价p(元/kg)与时间t(天)之间的函数关系式.
(2)哪一天的销售利润最大?最大日销售利润为多少?
八、(本题满分14分)
23.(14分)如图,将矩形纸片ABCD(AD>DC)的∠A沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边于点F.
(1)图中的全等三角形是 ,相似三角形是 .
(2)若BE:EC=1:4,CD=9,求BF的长;
(3)若BE:EC=m:n,求AF:FB.(用含有m,n的代数式表示)
2021-2022学年安徽省宣城市三县四校教学联盟九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)在下面的图形中,相似的一组是( )
A.
B.
C.
D.
【分析】根据相似图形的定义对各选项分析判断后利用排除法求解.
【解答】解:A、六边形与五边形不可能是相似图形,故本选项不符合题意;
B、两图形不是相似图形,故本选项不符合题意;
C、∵90°﹣40°=50°,
∴两三角形相似,故本选项符合题意;
D、两图形不是相似图形,故本选项不符合题意.
故选:C.
【点评】本题考查了相似图形的判定,是基础题,准确识图是解题的关键.
2.(4分)抛物线的解析式y=﹣2x2+1,则顶点坐标是( )
A.(﹣2,1) B.(0,1) C.(﹣2,﹣1) D.(0,﹣1)
【分析】本题解析式可理解为抛物线的顶点式,根据顶点式的坐标特点,直接写出顶点坐标.也可以利用顶点公式求解.
【解答】解:抛物线的解析式y=﹣2x2+1,则顶点坐标是(0,1),
故选:B.
【点评】本题主要考查了二次函数的性质,解题的关键是熟练掌握二次函数的顶点坐标式,此题难度不大.
3.(4分)若,则的值为( )
A. B.﹣ C. D.
【分析】把要求的式子化成+1,再把=代入进行计算,即可得出答案.
【解答】解:∵=,
∴=+1=+1=.
故选:D.
【点评】此题考查了比例的性质,熟练掌握比例的基本性质是解题的关键.
4.(4分)下列各点中,在反比例函数y=﹣图象上的是( )
A.(﹣1,4) B.(1,4) C.(﹣2,﹣2) D.(2,2)
【分析】由反比例函数图象中xy=k判断.
【解答】解:∵反比例函数y=﹣,
∴xy=﹣4,
选项A中﹣1×4=﹣4,满足题意.
选项B中1×4=4≠﹣4,不满足题意.
选项C中﹣2×(﹣2)=4≠﹣4,不满足题意.
选项D中2×2=4≠﹣4,不满足题意.
故选:A.
【点评】本题考查反比例函数图象上点的特征,解题关键是掌握xy=k.
5.(4分)某商场降价销售一批名牌球鞋,已知所获利润y(元)与降价金额x(元)之间满定函数关系式y=﹣x2+50x+600,若降价10元,则获利为( )
A.800元 B.600元 C.1200元 D.1000元
【分析】把x=10代入函数解析式即可.
【解答】解:当x=10时,y=﹣102+50×10+600=1000,
故选:D.
【点评】本题考查了二次函数的应用,关键是知道x的值求y.
6.(4分)若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=4m,BC=5cm,则矩形EFGH的周长是( )
A.12cm B.27cm C.24cm D.18cm
【分析】根据题意求出矩形ABCD的周长,根据相似三角形的周长之比等于相似比求出周长之比,计算即可.
【解答】解:∵AB=4cm,BC=5cm,
∴矩形ABCD的周长=2×(4+5)=18(cm),
∵矩形ABCD∽矩形EFGH,相似比为2:3,
∴矩形ABCD与矩形EFGH的周长比2:3,
∴矩形EFGH的周长为27cm,
故选:B.
【点评】本题考查的是相似多边形的性质,掌握相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方是解题的关键.
7.(4分)“计里画方”(比例缩放和直角坐标网格体系)是中国古代地图制图的基本方法和数学基础,是中国古代地图独立发展的重要标志.制作地图时,人们会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
【分析】由平行得相似,由相似得比例,即可作出判断.
【解答】解:∵EF∥AB,
∴△CEF∽△CAB,
∴==,
故选:C.
【点评】此题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解本题的关键.
8.(4分)二次函数y=ax2+bx+c(abc≠0)的图象如图所示,反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象是( )
A. B.
C. D.
【分析】由已知二次函数y=ax2+bx+c的图象开口方向和对称轴可以确定b的取值范围,由图象与y轴的交点可以确定C的取值范围,然后就可以确定反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象.
【解答】解:∵二次函数y=ax2+bx+c的图象开口方向向上,
∴a>0,
∵对称轴在y轴的右边,
∴x=﹣>0,
∴b<0,
∵二次函数y=ax2+bx+c的图象交y轴的正半轴,
∴c>0,
∴反比例函数y=的图象在第一三象限,
正比例函数y=bx的图象在第二四象限,
故选:D.
【点评】本题考查了二次函数的性质,利用函数图象的开口方向,对称轴以及与y轴的交点得出b、c的取值范围是解题关键.
9.(4分)如图,在△ABC中,∠A=60°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,有如下几种剪法,其中满足剪下的阴影三角形与△ABC相似的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据相似三角形的判定定理对各选项进行逐一判定即可.
【解答】解:第一个图形两边对应成比例,但夹角不一定相等,故两三角形不一定相似,故本选项不符合题意;
第二个图形阴影三角形中,∠A的两边分别为6﹣4=2,4﹣1=3,则两三角形对应边成比例且夹角相等,故两三角形相似,故本选项符合题意;
第三个图形阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项符合题意;
第四个图形阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项符合题意;
故选:C.
【点评】本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.
10.(4分)如图,点C、A、M、N在同一条直线l上.其中,△ABC是等腰直角三角形,∠B=90°,四边形MNPQ为正方形,且AC=4,MN=2,将等腰Rt△ABC沿直线l向右平移.若起始位置为点A与点M重合,终止位置为点C与点N重合.设点A平移的距离为x,两个图形重叠部分的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
【分析】根据动点的运动过程确定每段阴影部分与x的关系类型,根据函数的性质确定选项.
【解答】解:当x≤2时,重合部分是边长为x的等腰直角三角形,
面积为:y=x2,是一个开口向上的二次函数;
当2<x≤4时,重合部分面积为:y=4﹣(4﹣x)2﹣(x﹣2)2是一个开口向下的二次函数;
当4<x≤6时,重合部分面积为:y=(6﹣x)2,是一个开口向上是的二次函数.
故选:D.
【点评】本题考查了动点问题的函数图象,解决本题的关键是确定每段阴影部分与x的关系类型,根据函数的性质确定选项.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)二次函数y=(3﹣x)2图象的开口向 上 .
【分析】根据二次函数二次项的系数的符号确定开口方向即可.
【解答】解:∵二次函数y=(3﹣x)2中,a=>0,
∴开口向上,
故答案为:上.
【点评】本题考查了二次函数的图象和性质,二次函数的二次项的系数决定了开口的方向,难度较小.
12.(5分)如果两个相似多边形面积的比为25:49,则它们的相似比为 5:7 .
【分析】根据相似多边形的面积比等于相似比的平方计算即可.
【解答】解:∵两个相似多边形面积的比为25:49,
∴这两个相似多边形相似比为5:7,
故答案为:5:7.
【点评】本题考查的是相似多边形的性质,掌握相似多边形的面积比等于相似比的平方是解题的关键.
13.(5分)如图,已知一次函数y=ax(a<0)与反比例函数y=(x<0)的图象相交于点A,过点A作AB⊥y轴,垂足为B,若△OAB的面积为4,则k的值为 ﹣8 .
【分析】根据反比例函数的比例系数k的几何意义得到|k|=4,然后去绝对值即可得到满足条件的k的值.
【解答】解:∵AB⊥y轴,
∴S△OAB=|k|,
∴|k|=4,
∵k<0,
∴k=﹣8.
故答案为:﹣8.
【点评】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
14.(5分)如图,在平行四边形ABCD中,AC,BD相交于点O,E是OA的中点,连接BE并延长交AD于点F.
(1)= 2 .
(2)若△AEF的面积为4,则平行四边形ABCD的面积为 96 .
【分析】(1)根据四边形ABCD是平行四边形,可得OA=OC,AD∥BC,AD=BC,由点E是OA的中点,可得CE=3AE,再根据相似三角形对应边成比例即可得结论;
(2)由平行四边形的性质得出OA=OC,AD∥BC,证出CE=3AE,△AEF∽△CEB,得出=,△CEB的面积=36,求出△ABE的面积=△CEB的面积=12,得出△ABC的面积=48,即可得出平行四边形ABCD的面积.
【解答】解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,AD=BC,
∵点E是OA的中点,
∴CE=3AE,
∵AF∥BC,
∴△AEF∽△CEB,
∴==3,
∴BC=3AF,
∴FD=2AF,
∴=2;
故答案为:2;
(2)∵△AEF∽△CEB,
∴=()2=,
∴△CEB的面积=9×4=36,
∵CE=3AE,
∴△ABE的面积=△CEB的面积=12,
∴△ABC的面积=12+36=48,
∴平行四边形ABCD的面积=2△ABC的面积=2×48=96.
故答案为:96.
【点评】本题考查了相似三角形的判定与性质、三角形的面积、平行四边形的性质,解决本题的关键是掌握相似三角形的性质.
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知二次函数y=x2﹣2x﹣1,在平面直角坐标系中画出它的图象,并写出它的顶点坐标.
【分析】利用五点法画出函数图象即可,根据图象即可求得顶点坐标.
【解答】解:找出函数图象上部分点的坐标,列表:
x … ﹣1 0 1 2 3 …
y … 2 ﹣1 ﹣2 ﹣1 2 …
描点、连线,画出函数图象如图所示.
抛物线y=x2﹣2x﹣1的顶点坐标为(1,﹣2).
【点评】本题主要考查二次函数的图象,熟练掌握五点画图法是解题的关键.
16.(8分)已知反比例函数y=的图象经过点A(3,﹣2).
(1)求k的值.
(2)点A(x1,y1),B(x2,y2)均在反比例函数y=的图象上,若0<x1<x2,直接写出y1,y2的大小关系.
【分析】(1)把点A(3,﹣2)代入反比例函数解析式,即可求出k的值;
(2)由反比例函数的性质可直接得出结论.
【解答】解:(1)反比例函数y=的图象经过点A(3,﹣2).
∴2﹣k=3×(﹣2),解得k=8.
(2)由(1)知,反比例函数的解析式为:y=﹣,
∵﹣6<0,
∴在每一象限内,y随x的增大而增大,
∵点A(x1,y1),B(x2,y2)均在反比例函数y=的图象上,若0<x1<x2,
∴y2>y1.
【点评】题考查了待定系数法求解析式,反比例函数的性质等,熟练掌握反比例函数的性质是解题的关键.
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)如图,在△ABC中,点D、E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G.
(1)求证:△AED∽△ABC.
(2)若AG平分∠BAC,求证:.
【分析】(1)根据∠BAC=∠EAD公共角,∠AED=∠B,已知角,通过两角对应相等两个三角形相似来证明;
(2)通过AG平分∠BAC证一对角相等,再通过△AED∽△ABC证一对角相等,根据两角对应相等两个三角形相似来证明.
【解答】(1)证明:∵∠AED=∠B,∠BAC=∠EAD,
∴△AED∽△ABC;
(2)证明:∵AG平分∠BAC,
∴∠DAF=∠GAC,
∵△AED∽△ABC,
∴∠ADF=∠C,
∴△ADF∽△ACG,
∴.
【点评】本题主要考查了相似三角形的判定与性质,熟练掌握两角对应相等两个三角形相似这一判定定理是解题关键.
18.(8分)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象分别交x轴,y轴于A,B两点,与反比例函数y=(k≠0)的图象交于C,D两点,DE⊥x轴于点E,点C的坐标为(6,﹣1),DE=3.
(1)求反比例函数与一次函数的表达式;
(2)求△COD的面积.
【分析】(1)用待定系数法求出反比例函数表达式,进而求出点D的坐标,再利用待定系数法求出一次函数表达式即可求解;
(2)根据S△OCD=S△OAD+S△OAC求得即可.
【解答】解:(1)∵点C(6,﹣1)在反比例函数y=(k≠0)的图象上,
∴k=6×(﹣1)=﹣6,
∴反比例函数的关系式为y=﹣,
∵点D在反比例函数y=﹣上,且DE=3,
∴y=3,代入求得:x=﹣2,
∴点D的坐标为(﹣2,3).
∵C、D两点在直线y=ax+b上,则,解得,
∴一次函数的关系式为y=﹣x+2;
(2)把y=0代入y=﹣x+2,解得x=4,
即A(4,0),则OA=4,
S△OCD=S△OAD+S△OAC=×OA×(yD﹣yC)=×4×(3+1)=8.
【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,一次函数与坐标轴的交点,熟练掌握待定系数法是解本题的关键.
五、(本大题共2小题,每小题10分;满分20分)
19.(10分)如图,在四边形ABCD中,AD∥BC,∠BAD=90°,且BD⊥DC.
(1)△ABD与△DCB相似吗?请说明理由;
(2)若AD=4,BC=9,请求出BD的长.
【分析】(1)由AD∥BC,得∠ADB=∠DBC,而∠BAD=∠BDC=90°,即得△ABD∽△DCB;
(2)根据△ABD∽△DCB,得=,即=,故BD=6.
【解答】解:(1)△ABD与△DCB相似,理由如下:
∵AD∥BC,
∴∠ADB=∠DBC,
∵∠BAD=90°,且BD⊥DC,
∴∠BAD=∠BDC=90°,
∴△ABD∽△DCB;
(2)由(1)知△ABD∽△DCB,
∴=,
∵AD=4,BC=9,
∴=,
∴BD=6.
【点评】本题考查相似三角形的判定及性质,解题的关键是掌握三角形相似的判定定理.
20.(10分)如图,抛物线y=ax2+bx+4(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,求△PAC周长的最小值.
【分析】(1)待定系数法求解可得;
(2)连接BC,交直线l于点P,则此时△PAC的周长最小,先根据点B、C坐标求得直线BC的解析式,再结合直线l的解析式,求得点P的坐标,根据PA+PC+AC=PB+PC+AC=BC+AC,利用勾股定理即可得出答案.
【解答】解:(1)将点A(﹣2,0),B(6,0)代入y=ax2+bx+4,得:
,
解得:,
故该抛物线解析式为:y=﹣x2+x+4;
(2)如图,连接BC,交直线l于点P,则此时△PAC的周长最小,
在y=﹣x2+x+4中,当x=0时,y=4,
∴点C坐标为(0,4),
设BC所在直线解析式为y=kx+b,
将点B(6,0)、C(0,4)代入,得:,
解得:,
∴直线BC的解析式为y=﹣x+4,
又直线l的解析式为x==2,
∴直线l:x=2与直线BC:y=﹣x+4交点P的坐标为(2,),
∵点A与点B关于直线l对称,
∴PA=PB,
则PA+PC+AC
=PB+PC+AC
=BC+AC
=+
=2+2,
即△PAC的周长为2+2.
【点评】本题考查了抛物线与x轴的交点、二次函数的性质以及最短路径问题等知识,解题的关键是灵活应用这些知识解决问题,学会利用轴对称解决最短问题,学会用方程的思想思考问题,属于中考常考题型.
六、(本题满分12分)
21.(12分)某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,放置一个平面镜E来测量学校旗杆的高度,当镜子中心与旗杆的距离EB=20米,镜子中心与测量者的距离ED=2米时,测量者刚好从镜子中看到旗杆的顶端点A.已知测量者的身高为1.6米,测量者的眼睛距地面的高度为1.5米,求学校旗杆的高度是多少米.
(1)在计算过程中C,D之间的距离应是 1.5 米.
(2)根据以上测量结果,请你帮助“综合与实践”小组求出学校旗杆AB的高度.
(3)该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)
【分析】(1)根据题意可得出答案;
(2)根据反射定律可以推出∠1=∠2,所以可得△BAE∽△DCE,再根据相似三角形的性质解答.
(3)根据题意得到没有太阳光,或旗杆底部不可能达到相等(答案不唯一).
【解答】解:(1)∵测量者的眼睛距地面的高度为1.5米,
∴CD=1.5米.
故答案为:1.5;
(2)结合光的反射原理得:∠CED=∠AEB.
在Rt△CED和Rt△AEB中,
∵∠CDE=∠ABE=90°,∠CED=∠AEB,
∴Rt△CED∽Rt△AEB,
∴,
即,
解得AB=15(m).
答:铁塔AB的高度是15m.
(3)受天气条件影响,没有太阳光线,或旗杆底部不可能达到相等.
【点评】本题考查相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
七、(本题满分12分)
22.(12分)某地种植某种水果,其成本经过测算为20元/kg,投放市场后,经过市场调研发现,这种水果在上市的一段时间内的销售单价p(元/kg)与时间t(天)之间的函数图象如图所示,且其日销售量y(kg)与时间t(天)的关系是y=﹣2t+120,天数为整数.
(1)试求销售单价p(元/kg)与时间t(天)之间的函数关系式.
(2)哪一天的销售利润最大?最大日销售利润为多少?
【分析】(1)利用待定系数法求解析式;
(2)设日销售利润为w元,分别求出分段函数的中w的最大值,即可求解.
【解答】解:(1)当0≤t≤40时,设销售单价p(元/kg)与时间t(天)之间的函数关系式为p=kt+30,
∴40=40t+30,
∴t=,
∴p=t+30,
当t>40时,p=40,
综上所述:销售单价p(元/kg)与时间t(天)之间的函数关系式p=;
(2)设日销售利润为w元,
当0≤t≤40时,w=(p﹣20) y=(t+10)(﹣2t+120)=﹣(t﹣10)2+1250,
∴当t=10时,w有最大值为1250元,
当t>40时,w=(p﹣20) y=20(﹣2t+120)=﹣40t+2400<800,
∴第10天时,最大日销售利润为1250元.
【点评】本题考查了二次函数的应用,熟练运用二次函数的性质是本题的关键.
八、(本题满分14分)
23.(14分)如图,将矩形纸片ABCD(AD>DC)的∠A沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边于点F.
(1)图中的全等三角形是 △ADF≌△EDF ,相似三角形是 △FEB∽△EDC,△ADF∽△EDF .
(2)若BE:EC=1:4,CD=9,求BF的长;
(3)若BE:EC=m:n,求AF:FB.(用含有m,n的代数式表示)
【分析】(1)利用轴对称的性质可得全等三角形,利用同角的余角相等与矩形的性质以及相似三角形的判定解答即可;
(2)根据矩形的性质和相似三角形的性质解答即可;
(3)根据相似三角形的判定和性质解答即可.
【解答】(1)解:由翻折得,△ADF≌△EDF,
所以全等三角形是△ADF≌△EDF,
∵△ADF≌△EDF,四边形ABCD是矩形,
∴∠A=∠FED=90°,∠B=∠C=∠ADC=90°,
∴∠FEB+∠DEC=90°=∠DEC+∠EDC,
∴∠FEB=∠EDC,
∴△FEB∽△EDC,
由全等三角形是相似三角形的特例,
所以相似三角形有,△FEB∽△EDC,△ADF∽△EDF;
故答案为:△ADF≌△EDF;△FEB∽△EDC,△ADF∽△EDF;
(2)解:∵BE:EC=1:4,CD=9,
设BE=x,则EC=4x,BC=5x,
∵四边形ABCD是矩形,
∴AD=BC=5x,
由翻折得DE=AD=5x,
∴,
解得:x=3,
∴CE=12,BE=3,
∵△FEB∽△EDC,
∴,
∴;
(3)解:∵△FEB∽△EDC,
∴,
∵BE:EC=m:n,
设BE=mk,EC=nk,
则DE=AD=BC=(m+n)k,
∴,
由翻折得,AF=EF,
∴.
【点评】此题考查相似三角形的综合题,主要是通过折叠变换考查了三角形的有关知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,注意对应相等关系.
2021/12/9 8:10:24
第1页(共3页)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)在下面的图形中,相似的一组是( )
A.
B.
C.
D.
2.(4分)抛物线的解析式y=﹣2x2+1,则顶点坐标是( )
A.(﹣2,1) B.(0,1) C.(﹣2,﹣1) D.(0,﹣1)
3.(4分)若,则的值为( )
A. B.﹣ C. D.
4.(4分)下列各点中,在反比例函数y=﹣图象上的是( )
A.(﹣1,4) B.(1,4) C.(﹣2,﹣2) D.(2,2)
5.(4分)某商场降价销售一批名牌球鞋,已知所获利润y(元)与降价金额x(元)之间满定函数关系式y=﹣x2+50x+600,若降价10元,则获利为( )
A.800元 B.600元 C.1200元 D.1000元
6.(4分)若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=4m,BC=5cm,则矩形EFGH的周长是( )
A.12cm B.27cm C.24cm D.18cm
7.(4分)“计里画方”(比例缩放和直角坐标网格体系)是中国古代地图制图的基本方法和数学基础,是中国古代地图独立发展的重要标志.制作地图时,人们会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
8.(4分)二次函数y=ax2+bx+c(abc≠0)的图象如图所示,反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象是( )
A. B.
C. D.
9.(4分)如图,在△ABC中,∠A=60°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,有如下几种剪法,其中满足剪下的阴影三角形与△ABC相似的个数有( )
A.1个 B.2个 C.3个 D.4个
10.(4分)如图,点C、A、M、N在同一条直线l上.其中,△ABC是等腰直角三角形,∠B=90°,四边形MNPQ为正方形,且AC=4,MN=2,将等腰Rt△ABC沿直线l向右平移.若起始位置为点A与点M重合,终止位置为点C与点N重合.设点A平移的距离为x,两个图形重叠部分的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)二次函数y=(3﹣x)2图象的开口向 .
12.(5分)如果两个相似多边形面积的比为25:49,则它们的相似比为 .
13.(5分)如图,已知一次函数y=ax(a<0)与反比例函数y=(x<0)的图象相交于点A,过点A作AB⊥y轴,垂足为B,若△OAB的面积为4,则k的值为 .
14.(5分)如图,在平行四边形ABCD中,AC,BD相交于点O,E是OA的中点,连接BE并延长交AD于点F.
(1)= .
(2)若△AEF的面积为4,则平行四边形ABCD的面积为 .
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知二次函数y=x2﹣2x﹣1,在平面直角坐标系中画出它的图象,并写出它的顶点坐标.
16.(8分)已知反比例函数y=的图象经过点A(3,﹣2).
(1)求k的值.
(2)点A(x1,y1),B(x2,y2)均在反比例函数y=的图象上,若0<x1<x2,直接写出y1,y2的大小关系.
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)如图,在△ABC中,点D、E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G.
(1)求证:△AED∽△ABC.
(2)若AG平分∠BAC,求证:.
18.(8分)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象分别交x轴,y轴于A,B两点,与反比例函数y=(k≠0)的图象交于C,D两点,DE⊥x轴于点E,点C的坐标为(6,﹣1),DE=3.
(1)求反比例函数与一次函数的表达式;
(2)求△COD的面积.
五、(本大题共2小题,每小题10分;满分20分)
19.(10分)如图,在四边形ABCD中,AD∥BC,∠BAD=90°,且BD⊥DC.
(1)△ABD与△DCB相似吗?请说明理由;
(2)若AD=4,BC=9,请求出BD的长.
20.(10分)如图,抛物线y=ax2+bx+4(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,求△PAC周长的最小值.
六、(本题满分12分)
21.(12分)某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,放置一个平面镜E来测量学校旗杆的高度,当镜子中心与旗杆的距离EB=20米,镜子中心与测量者的距离ED=2米时,测量者刚好从镜子中看到旗杆的顶端点A.已知测量者的身高为1.6米,测量者的眼睛距地面的高度为1.5米,求学校旗杆的高度是多少米.
(1)在计算过程中C,D之间的距离应是 米.
(2)根据以上测量结果,请你帮助“综合与实践”小组求出学校旗杆AB的高度.
(3)该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)
七、(本题满分12分)
22.(12分)某地种植某种水果,其成本经过测算为20元/kg,投放市场后,经过市场调研发现,这种水果在上市的一段时间内的销售单价p(元/kg)与时间t(天)之间的函数图象如图所示,且其日销售量y(kg)与时间t(天)的关系是y=﹣2t+120,天数为整数.
(1)试求销售单价p(元/kg)与时间t(天)之间的函数关系式.
(2)哪一天的销售利润最大?最大日销售利润为多少?
八、(本题满分14分)
23.(14分)如图,将矩形纸片ABCD(AD>DC)的∠A沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边于点F.
(1)图中的全等三角形是 ,相似三角形是 .
(2)若BE:EC=1:4,CD=9,求BF的长;
(3)若BE:EC=m:n,求AF:FB.(用含有m,n的代数式表示)
2021-2022学年安徽省宣城市三县四校教学联盟九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)在下面的图形中,相似的一组是( )
A.
B.
C.
D.
【分析】根据相似图形的定义对各选项分析判断后利用排除法求解.
【解答】解:A、六边形与五边形不可能是相似图形,故本选项不符合题意;
B、两图形不是相似图形,故本选项不符合题意;
C、∵90°﹣40°=50°,
∴两三角形相似,故本选项符合题意;
D、两图形不是相似图形,故本选项不符合题意.
故选:C.
【点评】本题考查了相似图形的判定,是基础题,准确识图是解题的关键.
2.(4分)抛物线的解析式y=﹣2x2+1,则顶点坐标是( )
A.(﹣2,1) B.(0,1) C.(﹣2,﹣1) D.(0,﹣1)
【分析】本题解析式可理解为抛物线的顶点式,根据顶点式的坐标特点,直接写出顶点坐标.也可以利用顶点公式求解.
【解答】解:抛物线的解析式y=﹣2x2+1,则顶点坐标是(0,1),
故选:B.
【点评】本题主要考查了二次函数的性质,解题的关键是熟练掌握二次函数的顶点坐标式,此题难度不大.
3.(4分)若,则的值为( )
A. B.﹣ C. D.
【分析】把要求的式子化成+1,再把=代入进行计算,即可得出答案.
【解答】解:∵=,
∴=+1=+1=.
故选:D.
【点评】此题考查了比例的性质,熟练掌握比例的基本性质是解题的关键.
4.(4分)下列各点中,在反比例函数y=﹣图象上的是( )
A.(﹣1,4) B.(1,4) C.(﹣2,﹣2) D.(2,2)
【分析】由反比例函数图象中xy=k判断.
【解答】解:∵反比例函数y=﹣,
∴xy=﹣4,
选项A中﹣1×4=﹣4,满足题意.
选项B中1×4=4≠﹣4,不满足题意.
选项C中﹣2×(﹣2)=4≠﹣4,不满足题意.
选项D中2×2=4≠﹣4,不满足题意.
故选:A.
【点评】本题考查反比例函数图象上点的特征,解题关键是掌握xy=k.
5.(4分)某商场降价销售一批名牌球鞋,已知所获利润y(元)与降价金额x(元)之间满定函数关系式y=﹣x2+50x+600,若降价10元,则获利为( )
A.800元 B.600元 C.1200元 D.1000元
【分析】把x=10代入函数解析式即可.
【解答】解:当x=10时,y=﹣102+50×10+600=1000,
故选:D.
【点评】本题考查了二次函数的应用,关键是知道x的值求y.
6.(4分)若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=4m,BC=5cm,则矩形EFGH的周长是( )
A.12cm B.27cm C.24cm D.18cm
【分析】根据题意求出矩形ABCD的周长,根据相似三角形的周长之比等于相似比求出周长之比,计算即可.
【解答】解:∵AB=4cm,BC=5cm,
∴矩形ABCD的周长=2×(4+5)=18(cm),
∵矩形ABCD∽矩形EFGH,相似比为2:3,
∴矩形ABCD与矩形EFGH的周长比2:3,
∴矩形EFGH的周长为27cm,
故选:B.
【点评】本题考查的是相似多边形的性质,掌握相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方是解题的关键.
7.(4分)“计里画方”(比例缩放和直角坐标网格体系)是中国古代地图制图的基本方法和数学基础,是中国古代地图独立发展的重要标志.制作地图时,人们会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确的是( )
A. B. C. D.
【分析】由平行得相似,由相似得比例,即可作出判断.
【解答】解:∵EF∥AB,
∴△CEF∽△CAB,
∴==,
故选:C.
【点评】此题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解本题的关键.
8.(4分)二次函数y=ax2+bx+c(abc≠0)的图象如图所示,反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象是( )
A. B.
C. D.
【分析】由已知二次函数y=ax2+bx+c的图象开口方向和对称轴可以确定b的取值范围,由图象与y轴的交点可以确定C的取值范围,然后就可以确定反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象.
【解答】解:∵二次函数y=ax2+bx+c的图象开口方向向上,
∴a>0,
∵对称轴在y轴的右边,
∴x=﹣>0,
∴b<0,
∵二次函数y=ax2+bx+c的图象交y轴的正半轴,
∴c>0,
∴反比例函数y=的图象在第一三象限,
正比例函数y=bx的图象在第二四象限,
故选:D.
【点评】本题考查了二次函数的性质,利用函数图象的开口方向,对称轴以及与y轴的交点得出b、c的取值范围是解题关键.
9.(4分)如图,在△ABC中,∠A=60°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,有如下几种剪法,其中满足剪下的阴影三角形与△ABC相似的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据相似三角形的判定定理对各选项进行逐一判定即可.
【解答】解:第一个图形两边对应成比例,但夹角不一定相等,故两三角形不一定相似,故本选项不符合题意;
第二个图形阴影三角形中,∠A的两边分别为6﹣4=2,4﹣1=3,则两三角形对应边成比例且夹角相等,故两三角形相似,故本选项符合题意;
第三个图形阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项符合题意;
第四个图形阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项符合题意;
故选:C.
【点评】本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.
10.(4分)如图,点C、A、M、N在同一条直线l上.其中,△ABC是等腰直角三角形,∠B=90°,四边形MNPQ为正方形,且AC=4,MN=2,将等腰Rt△ABC沿直线l向右平移.若起始位置为点A与点M重合,终止位置为点C与点N重合.设点A平移的距离为x,两个图形重叠部分的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
【分析】根据动点的运动过程确定每段阴影部分与x的关系类型,根据函数的性质确定选项.
【解答】解:当x≤2时,重合部分是边长为x的等腰直角三角形,
面积为:y=x2,是一个开口向上的二次函数;
当2<x≤4时,重合部分面积为:y=4﹣(4﹣x)2﹣(x﹣2)2是一个开口向下的二次函数;
当4<x≤6时,重合部分面积为:y=(6﹣x)2,是一个开口向上是的二次函数.
故选:D.
【点评】本题考查了动点问题的函数图象,解决本题的关键是确定每段阴影部分与x的关系类型,根据函数的性质确定选项.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)二次函数y=(3﹣x)2图象的开口向 上 .
【分析】根据二次函数二次项的系数的符号确定开口方向即可.
【解答】解:∵二次函数y=(3﹣x)2中,a=>0,
∴开口向上,
故答案为:上.
【点评】本题考查了二次函数的图象和性质,二次函数的二次项的系数决定了开口的方向,难度较小.
12.(5分)如果两个相似多边形面积的比为25:49,则它们的相似比为 5:7 .
【分析】根据相似多边形的面积比等于相似比的平方计算即可.
【解答】解:∵两个相似多边形面积的比为25:49,
∴这两个相似多边形相似比为5:7,
故答案为:5:7.
【点评】本题考查的是相似多边形的性质,掌握相似多边形的面积比等于相似比的平方是解题的关键.
13.(5分)如图,已知一次函数y=ax(a<0)与反比例函数y=(x<0)的图象相交于点A,过点A作AB⊥y轴,垂足为B,若△OAB的面积为4,则k的值为 ﹣8 .
【分析】根据反比例函数的比例系数k的几何意义得到|k|=4,然后去绝对值即可得到满足条件的k的值.
【解答】解:∵AB⊥y轴,
∴S△OAB=|k|,
∴|k|=4,
∵k<0,
∴k=﹣8.
故答案为:﹣8.
【点评】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
14.(5分)如图,在平行四边形ABCD中,AC,BD相交于点O,E是OA的中点,连接BE并延长交AD于点F.
(1)= 2 .
(2)若△AEF的面积为4,则平行四边形ABCD的面积为 96 .
【分析】(1)根据四边形ABCD是平行四边形,可得OA=OC,AD∥BC,AD=BC,由点E是OA的中点,可得CE=3AE,再根据相似三角形对应边成比例即可得结论;
(2)由平行四边形的性质得出OA=OC,AD∥BC,证出CE=3AE,△AEF∽△CEB,得出=,△CEB的面积=36,求出△ABE的面积=△CEB的面积=12,得出△ABC的面积=48,即可得出平行四边形ABCD的面积.
【解答】解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,AD=BC,
∵点E是OA的中点,
∴CE=3AE,
∵AF∥BC,
∴△AEF∽△CEB,
∴==3,
∴BC=3AF,
∴FD=2AF,
∴=2;
故答案为:2;
(2)∵△AEF∽△CEB,
∴=()2=,
∴△CEB的面积=9×4=36,
∵CE=3AE,
∴△ABE的面积=△CEB的面积=12,
∴△ABC的面积=12+36=48,
∴平行四边形ABCD的面积=2△ABC的面积=2×48=96.
故答案为:96.
【点评】本题考查了相似三角形的判定与性质、三角形的面积、平行四边形的性质,解决本题的关键是掌握相似三角形的性质.
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)已知二次函数y=x2﹣2x﹣1,在平面直角坐标系中画出它的图象,并写出它的顶点坐标.
【分析】利用五点法画出函数图象即可,根据图象即可求得顶点坐标.
【解答】解:找出函数图象上部分点的坐标,列表:
x … ﹣1 0 1 2 3 …
y … 2 ﹣1 ﹣2 ﹣1 2 …
描点、连线,画出函数图象如图所示.
抛物线y=x2﹣2x﹣1的顶点坐标为(1,﹣2).
【点评】本题主要考查二次函数的图象,熟练掌握五点画图法是解题的关键.
16.(8分)已知反比例函数y=的图象经过点A(3,﹣2).
(1)求k的值.
(2)点A(x1,y1),B(x2,y2)均在反比例函数y=的图象上,若0<x1<x2,直接写出y1,y2的大小关系.
【分析】(1)把点A(3,﹣2)代入反比例函数解析式,即可求出k的值;
(2)由反比例函数的性质可直接得出结论.
【解答】解:(1)反比例函数y=的图象经过点A(3,﹣2).
∴2﹣k=3×(﹣2),解得k=8.
(2)由(1)知,反比例函数的解析式为:y=﹣,
∵﹣6<0,
∴在每一象限内,y随x的增大而增大,
∵点A(x1,y1),B(x2,y2)均在反比例函数y=的图象上,若0<x1<x2,
∴y2>y1.
【点评】题考查了待定系数法求解析式,反比例函数的性质等,熟练掌握反比例函数的性质是解题的关键.
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)如图,在△ABC中,点D、E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G.
(1)求证:△AED∽△ABC.
(2)若AG平分∠BAC,求证:.
【分析】(1)根据∠BAC=∠EAD公共角,∠AED=∠B,已知角,通过两角对应相等两个三角形相似来证明;
(2)通过AG平分∠BAC证一对角相等,再通过△AED∽△ABC证一对角相等,根据两角对应相等两个三角形相似来证明.
【解答】(1)证明:∵∠AED=∠B,∠BAC=∠EAD,
∴△AED∽△ABC;
(2)证明:∵AG平分∠BAC,
∴∠DAF=∠GAC,
∵△AED∽△ABC,
∴∠ADF=∠C,
∴△ADF∽△ACG,
∴.
【点评】本题主要考查了相似三角形的判定与性质,熟练掌握两角对应相等两个三角形相似这一判定定理是解题关键.
18.(8分)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象分别交x轴,y轴于A,B两点,与反比例函数y=(k≠0)的图象交于C,D两点,DE⊥x轴于点E,点C的坐标为(6,﹣1),DE=3.
(1)求反比例函数与一次函数的表达式;
(2)求△COD的面积.
【分析】(1)用待定系数法求出反比例函数表达式,进而求出点D的坐标,再利用待定系数法求出一次函数表达式即可求解;
(2)根据S△OCD=S△OAD+S△OAC求得即可.
【解答】解:(1)∵点C(6,﹣1)在反比例函数y=(k≠0)的图象上,
∴k=6×(﹣1)=﹣6,
∴反比例函数的关系式为y=﹣,
∵点D在反比例函数y=﹣上,且DE=3,
∴y=3,代入求得:x=﹣2,
∴点D的坐标为(﹣2,3).
∵C、D两点在直线y=ax+b上,则,解得,
∴一次函数的关系式为y=﹣x+2;
(2)把y=0代入y=﹣x+2,解得x=4,
即A(4,0),则OA=4,
S△OCD=S△OAD+S△OAC=×OA×(yD﹣yC)=×4×(3+1)=8.
【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,一次函数与坐标轴的交点,熟练掌握待定系数法是解本题的关键.
五、(本大题共2小题,每小题10分;满分20分)
19.(10分)如图,在四边形ABCD中,AD∥BC,∠BAD=90°,且BD⊥DC.
(1)△ABD与△DCB相似吗?请说明理由;
(2)若AD=4,BC=9,请求出BD的长.
【分析】(1)由AD∥BC,得∠ADB=∠DBC,而∠BAD=∠BDC=90°,即得△ABD∽△DCB;
(2)根据△ABD∽△DCB,得=,即=,故BD=6.
【解答】解:(1)△ABD与△DCB相似,理由如下:
∵AD∥BC,
∴∠ADB=∠DBC,
∵∠BAD=90°,且BD⊥DC,
∴∠BAD=∠BDC=90°,
∴△ABD∽△DCB;
(2)由(1)知△ABD∽△DCB,
∴=,
∵AD=4,BC=9,
∴=,
∴BD=6.
【点评】本题考查相似三角形的判定及性质,解题的关键是掌握三角形相似的判定定理.
20.(10分)如图,抛物线y=ax2+bx+4(a≠0)与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C,抛物线的对称轴l与x轴交于点M.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,求△PAC周长的最小值.
【分析】(1)待定系数法求解可得;
(2)连接BC,交直线l于点P,则此时△PAC的周长最小,先根据点B、C坐标求得直线BC的解析式,再结合直线l的解析式,求得点P的坐标,根据PA+PC+AC=PB+PC+AC=BC+AC,利用勾股定理即可得出答案.
【解答】解:(1)将点A(﹣2,0),B(6,0)代入y=ax2+bx+4,得:
,
解得:,
故该抛物线解析式为:y=﹣x2+x+4;
(2)如图,连接BC,交直线l于点P,则此时△PAC的周长最小,
在y=﹣x2+x+4中,当x=0时,y=4,
∴点C坐标为(0,4),
设BC所在直线解析式为y=kx+b,
将点B(6,0)、C(0,4)代入,得:,
解得:,
∴直线BC的解析式为y=﹣x+4,
又直线l的解析式为x==2,
∴直线l:x=2与直线BC:y=﹣x+4交点P的坐标为(2,),
∵点A与点B关于直线l对称,
∴PA=PB,
则PA+PC+AC
=PB+PC+AC
=BC+AC
=+
=2+2,
即△PAC的周长为2+2.
【点评】本题考查了抛物线与x轴的交点、二次函数的性质以及最短路径问题等知识,解题的关键是灵活应用这些知识解决问题,学会利用轴对称解决最短问题,学会用方程的思想思考问题,属于中考常考题型.
六、(本题满分12分)
21.(12分)某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,放置一个平面镜E来测量学校旗杆的高度,当镜子中心与旗杆的距离EB=20米,镜子中心与测量者的距离ED=2米时,测量者刚好从镜子中看到旗杆的顶端点A.已知测量者的身高为1.6米,测量者的眼睛距地面的高度为1.5米,求学校旗杆的高度是多少米.
(1)在计算过程中C,D之间的距离应是 1.5 米.
(2)根据以上测量结果,请你帮助“综合与实践”小组求出学校旗杆AB的高度.
(3)该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)
【分析】(1)根据题意可得出答案;
(2)根据反射定律可以推出∠1=∠2,所以可得△BAE∽△DCE,再根据相似三角形的性质解答.
(3)根据题意得到没有太阳光,或旗杆底部不可能达到相等(答案不唯一).
【解答】解:(1)∵测量者的眼睛距地面的高度为1.5米,
∴CD=1.5米.
故答案为:1.5;
(2)结合光的反射原理得:∠CED=∠AEB.
在Rt△CED和Rt△AEB中,
∵∠CDE=∠ABE=90°,∠CED=∠AEB,
∴Rt△CED∽Rt△AEB,
∴,
即,
解得AB=15(m).
答:铁塔AB的高度是15m.
(3)受天气条件影响,没有太阳光线,或旗杆底部不可能达到相等.
【点评】本题考查相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
七、(本题满分12分)
22.(12分)某地种植某种水果,其成本经过测算为20元/kg,投放市场后,经过市场调研发现,这种水果在上市的一段时间内的销售单价p(元/kg)与时间t(天)之间的函数图象如图所示,且其日销售量y(kg)与时间t(天)的关系是y=﹣2t+120,天数为整数.
(1)试求销售单价p(元/kg)与时间t(天)之间的函数关系式.
(2)哪一天的销售利润最大?最大日销售利润为多少?
【分析】(1)利用待定系数法求解析式;
(2)设日销售利润为w元,分别求出分段函数的中w的最大值,即可求解.
【解答】解:(1)当0≤t≤40时,设销售单价p(元/kg)与时间t(天)之间的函数关系式为p=kt+30,
∴40=40t+30,
∴t=,
∴p=t+30,
当t>40时,p=40,
综上所述:销售单价p(元/kg)与时间t(天)之间的函数关系式p=;
(2)设日销售利润为w元,
当0≤t≤40时,w=(p﹣20) y=(t+10)(﹣2t+120)=﹣(t﹣10)2+1250,
∴当t=10时,w有最大值为1250元,
当t>40时,w=(p﹣20) y=20(﹣2t+120)=﹣40t+2400<800,
∴第10天时,最大日销售利润为1250元.
【点评】本题考查了二次函数的应用,熟练运用二次函数的性质是本题的关键.
八、(本题满分14分)
23.(14分)如图,将矩形纸片ABCD(AD>DC)的∠A沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边于点F.
(1)图中的全等三角形是 △ADF≌△EDF ,相似三角形是 △FEB∽△EDC,△ADF∽△EDF .
(2)若BE:EC=1:4,CD=9,求BF的长;
(3)若BE:EC=m:n,求AF:FB.(用含有m,n的代数式表示)
【分析】(1)利用轴对称的性质可得全等三角形,利用同角的余角相等与矩形的性质以及相似三角形的判定解答即可;
(2)根据矩形的性质和相似三角形的性质解答即可;
(3)根据相似三角形的判定和性质解答即可.
【解答】(1)解:由翻折得,△ADF≌△EDF,
所以全等三角形是△ADF≌△EDF,
∵△ADF≌△EDF,四边形ABCD是矩形,
∴∠A=∠FED=90°,∠B=∠C=∠ADC=90°,
∴∠FEB+∠DEC=90°=∠DEC+∠EDC,
∴∠FEB=∠EDC,
∴△FEB∽△EDC,
由全等三角形是相似三角形的特例,
所以相似三角形有,△FEB∽△EDC,△ADF∽△EDF;
故答案为:△ADF≌△EDF;△FEB∽△EDC,△ADF∽△EDF;
(2)解:∵BE:EC=1:4,CD=9,
设BE=x,则EC=4x,BC=5x,
∵四边形ABCD是矩形,
∴AD=BC=5x,
由翻折得DE=AD=5x,
∴,
解得:x=3,
∴CE=12,BE=3,
∵△FEB∽△EDC,
∴,
∴;
(3)解:∵△FEB∽△EDC,
∴,
∵BE:EC=m:n,
设BE=mk,EC=nk,
则DE=AD=BC=(m+n)k,
∴,
由翻折得,AF=EF,
∴.
【点评】此题考查相似三角形的综合题,主要是通过折叠变换考查了三角形的有关知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,注意对应相等关系.
2021/12/9 8:10:24
第1页(共3页)
同课章节目录
