北京课改版数学七年级下册第六章 整式的运算期末测试试卷(word版含答案)独家版权
文档属性
| 名称 | 北京课改版数学七年级下册第六章 整式的运算期末测试试卷(word版含答案)独家版权 |

|
|
| 格式 | zip | ||
| 文件大小 | 107.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览



文档简介
北京课改版数学七年级下册第六章 整式的运算期末测试试卷
一、选择题(共10小题;共50分)
1. 下列等式成立的是
A. B.
C. D.
2. 下面计算中:① ;② ;③ ;④ ;⑤ ;⑥ .其中做对的题有
A. 道 B. 道 C. 道 D. 道
3. 下列算式中,计算结果为 的是
A. B.
C. D.
4. 等式 成立的条件是
A. B. C. D. 为有理数
5. 若 ,则 , 的值分别为
A. , B. , C. , D. ,
6. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图①可以得到 ,那么利用图②所得到的数学等式是
A.
B.
C.
D.
7. 计算 的结果是
A. B. C. D.
8. 一套住房的平面图如图所示,其中卫生间、厨房的面积和是
A. B. C. D.
9. 若 ,则
A. B. C. D.
10. 我国宋朝数学家杨辉 年的著作《详解九章算法》给出了在 ( 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 计算: .
12. 下列是用科学记数法表示的数,写出原来的数.
() ;
() .
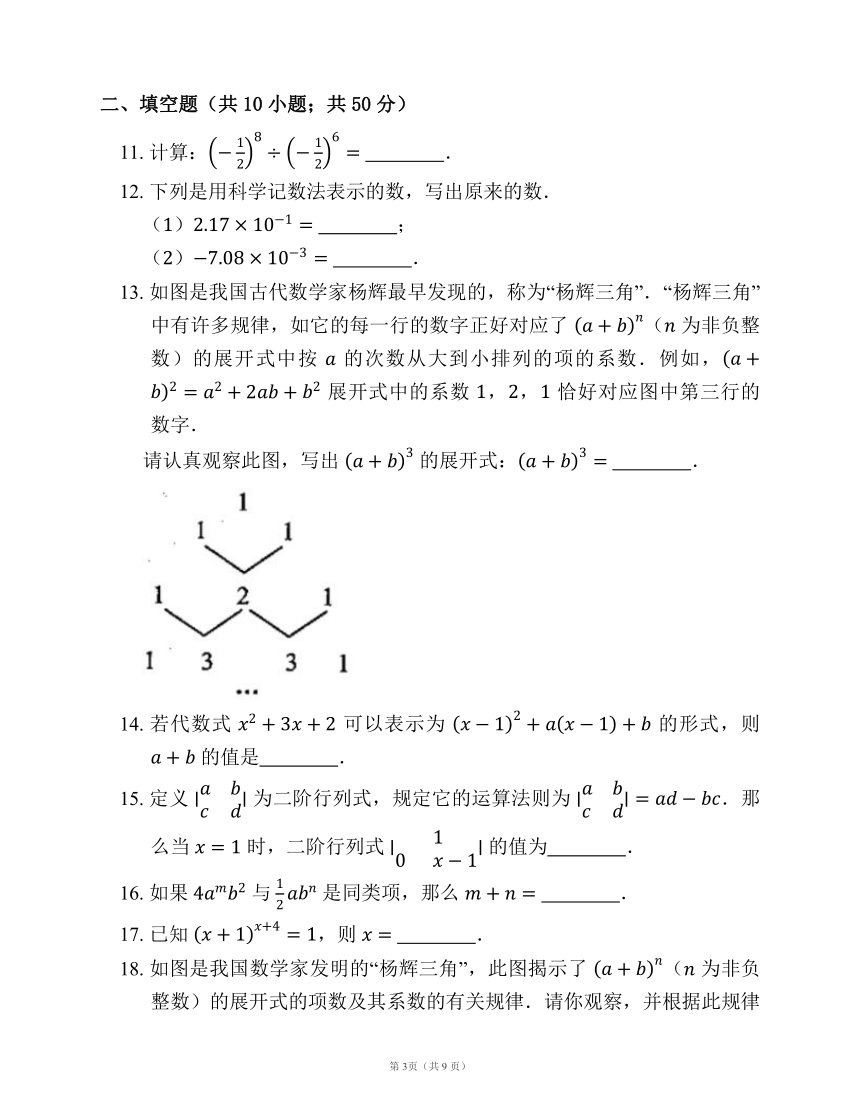
13. 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了 ( 为非负整数)的展开式中按 的次数从大到小排列的项的系数.例如, 展开式中的系数 ,, 恰好对应图中第三行的数字.
请认真观察此图,写出 的展开式: .
14. 若代数式 可以表示为 的形式,则 的值是 .
15. 定义 为二阶行列式,规定它的运算法则为 .那么当 时,二阶行列式 的值为 .
16. 如果 与 是同类项,那么 .
17. 已知 ,则 .
18. 如图是我国数学家发明的“杨辉三角”,此图揭示了 ( 为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出 的展开式共有 项,第二项的系数是 , 的展开式共有 项,各项的系数和是 .
19. 某同学计算 的过程如下:
模仿这位同学的运算方法,计算:
.
20. 设 ,,.若 ,,则 .
三、解答题(共6小题;共50分)
21. 求 与 的和.
22. 根据完全平方公式 填空:
(1);
(2);
(3);
(4).
23. 已知x+y=7,xy=6,求:
(1)x﹣y的值;
(2) 的值.
24. 阅读以下材料:;;;
(1)根据以上规律, ;
(2)利用()的结论,求 的值.
25. 计算:
(1);
(2).
26. 观察下列一组等式:
;
;
.
(1)从以上等式中,你有何发现 利用你发现的规律,在下面括号中添上适当的式子.
① ;
② ( );
③( ).
(2)计算:.
答案
第一部分
1. B 【解析】,选项A错误,选项B正确;
,选项C错误;
,选项D错误.
2. B 【解析】① ,正确;
② ,错误;
③ ,错误;
④ ,错误;
⑤ ,错误;
⑥ ,正确.
正确的有 道.故B正确.
3. A
4. C
5. D
6. B 【解析】从整体看:正方形的面积 ,
从局部看:正方形的面积 ,
所以 .
7. B
8. B 【解析】.
9. B
10. D
【解析】由题意,,
可知,展开式中第二项为 ,
所以 展开式中含 项的系数是 .
第二部分
11.
12. ,
13.
14.
【解析】
所以 ,.
所以 .
15.
16.
17. 或 或
【解析】①若 ,则 ,此时 ,符合题意;
②若 ,则 ,此时 ,符合题意;
③若 ,则 ,此时 ,符合题意.
综上所述,.
18. ,,,
【解析】 的展开式有 项; 的展开式有 项; 的展开式有 项; 故 的展开式共有 项.由题中规律得 的展开式中第二项的系数为 , 的展开式中第二项的系数为 ,故 的展开式中第二项的系数为 .
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
故 的展开式中各项的系数和为 .
19.
20.
【解析】由题意得 ,
,
,
,
.
第三部分
21. .
22. (1)
(2) ;
(3) ;
(4) ;
23. (1) ,
【解析】略
(2) 67 或 7
【解析】 当 时,原式 ;当 时,原式 .故 的值为 67 或 7 .
24. (1)
【解析】.
(2)
25. (1)
(2)
26. (1) ① ;② ;③
(2) .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 下列等式成立的是
A. B.
C. D.
2. 下面计算中:① ;② ;③ ;④ ;⑤ ;⑥ .其中做对的题有
A. 道 B. 道 C. 道 D. 道
3. 下列算式中,计算结果为 的是
A. B.
C. D.
4. 等式 成立的条件是
A. B. C. D. 为有理数
5. 若 ,则 , 的值分别为
A. , B. , C. , D. ,
6. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图①可以得到 ,那么利用图②所得到的数学等式是
A.
B.
C.
D.
7. 计算 的结果是
A. B. C. D.
8. 一套住房的平面图如图所示,其中卫生间、厨房的面积和是
A. B. C. D.
9. 若 ,则
A. B. C. D.
10. 我国宋朝数学家杨辉 年的著作《详解九章算法》给出了在 ( 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 计算: .
12. 下列是用科学记数法表示的数,写出原来的数.
() ;
() .
13. 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了 ( 为非负整数)的展开式中按 的次数从大到小排列的项的系数.例如, 展开式中的系数 ,, 恰好对应图中第三行的数字.
请认真观察此图,写出 的展开式: .
14. 若代数式 可以表示为 的形式,则 的值是 .
15. 定义 为二阶行列式,规定它的运算法则为 .那么当 时,二阶行列式 的值为 .
16. 如果 与 是同类项,那么 .
17. 已知 ,则 .
18. 如图是我国数学家发明的“杨辉三角”,此图揭示了 ( 为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出 的展开式共有 项,第二项的系数是 , 的展开式共有 项,各项的系数和是 .
19. 某同学计算 的过程如下:
模仿这位同学的运算方法,计算:
.
20. 设 ,,.若 ,,则 .
三、解答题(共6小题;共50分)
21. 求 与 的和.
22. 根据完全平方公式 填空:
(1);
(2);
(3);
(4).
23. 已知x+y=7,xy=6,求:
(1)x﹣y的值;
(2) 的值.
24. 阅读以下材料:;;;
(1)根据以上规律, ;
(2)利用()的结论,求 的值.
25. 计算:
(1);
(2).
26. 观察下列一组等式:
;
;
.
(1)从以上等式中,你有何发现 利用你发现的规律,在下面括号中添上适当的式子.
① ;
② ( );
③( ).
(2)计算:.
答案
第一部分
1. B 【解析】,选项A错误,选项B正确;
,选项C错误;
,选项D错误.
2. B 【解析】① ,正确;
② ,错误;
③ ,错误;
④ ,错误;
⑤ ,错误;
⑥ ,正确.
正确的有 道.故B正确.
3. A
4. C
5. D
6. B 【解析】从整体看:正方形的面积 ,
从局部看:正方形的面积 ,
所以 .
7. B
8. B 【解析】.
9. B
10. D
【解析】由题意,,
可知,展开式中第二项为 ,
所以 展开式中含 项的系数是 .
第二部分
11.
12. ,
13.
14.
【解析】
所以 ,.
所以 .
15.
16.
17. 或 或
【解析】①若 ,则 ,此时 ,符合题意;
②若 ,则 ,此时 ,符合题意;
③若 ,则 ,此时 ,符合题意.
综上所述,.
18. ,,,
【解析】 的展开式有 项; 的展开式有 项; 的展开式有 项; 故 的展开式共有 项.由题中规律得 的展开式中第二项的系数为 , 的展开式中第二项的系数为 ,故 的展开式中第二项的系数为 .
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
故 的展开式中各项的系数和为 .
19.
20.
【解析】由题意得 ,
,
,
,
.
第三部分
21. .
22. (1)
(2) ;
(3) ;
(4) ;
23. (1) ,
【解析】略
(2) 67 或 7
【解析】 当 时,原式 ;当 时,原式 .故 的值为 67 或 7 .
24. (1)
【解析】.
(2)
25. (1)
(2)
26. (1) ① ;② ;③
(2) .
第1页(共1 页)
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
