北京课改版数学九年级第二十二章 圆(下)试卷(word版含答案)
文档属性
| 名称 | 北京课改版数学九年级第二十二章 圆(下)试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 766.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 06:04:09 | ||
图片预览


文档简介
第二十二章 圆(下)
一、选择题(共10小题;共50分)
1. 直线 与半径为 的 相交,且点 到直线 的距离为 ,则 的取值范围是
A. B. C. D.
2. 下列命题中正确的是
A. 垂直于半径的直线是圆的切线
B. 经过半径外端的直线是圆的切线
C. 经过切点的直线是圆的切线
D. 圆心到某直线的距离等于半径,那么这条直线是圆的切线
3. 已知 ,,,以点 为圆心 为半径作圆,如果点 、点 只有一个点在圆内,那么半径 的取值范围是
A. B. C. D.
4. 已知 的半径 , 的圆心到直线 的距离 ,则直线 与 的位置关系是
A. 相离 B. 相交 C. 相切 D. 无法确定
5. 下列命题中,正确的是
A. 平分一条直径的弦必垂直于这条直径
B. 平分一条弧的直线垂直于这条弧所对的弦
C. 弦的垂线必经过这条弦所在圆的圆心
D. 在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心
6. 如图, 为 的直径,点 , 是 的三等分点,,则 的度数为
A. B. C. D.
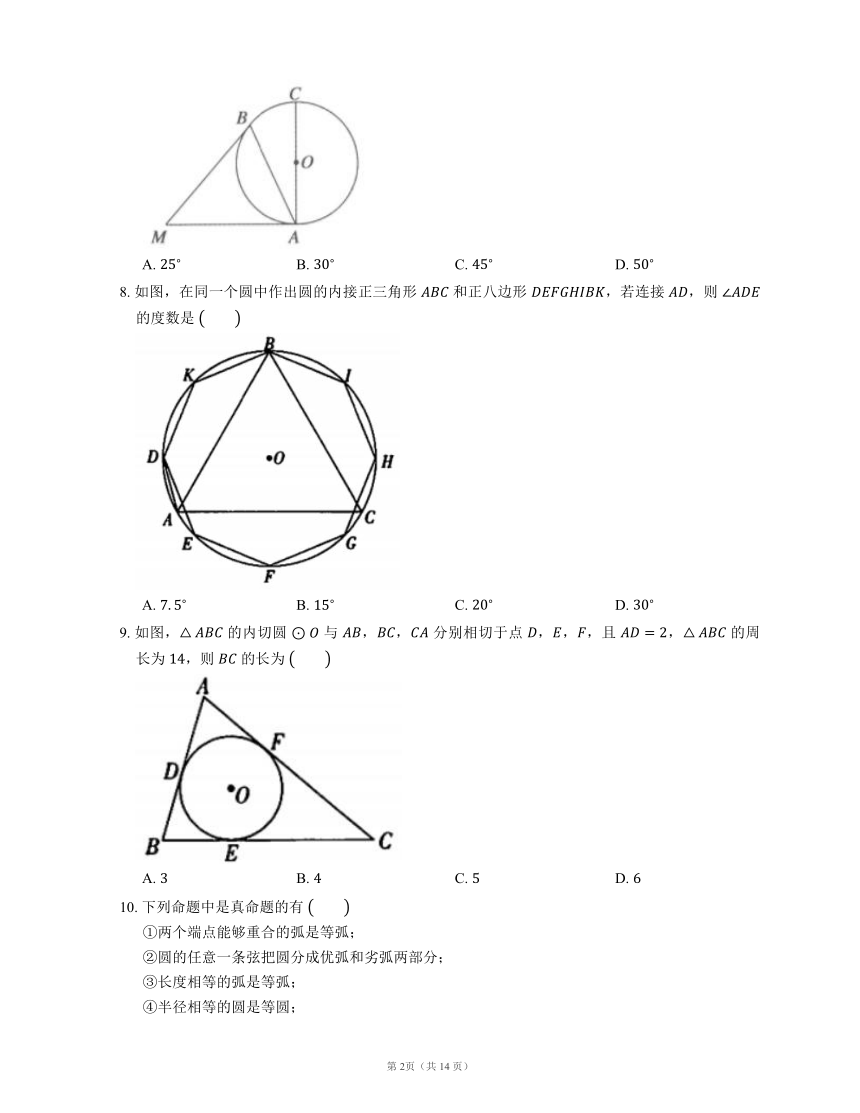
7. 如图, 中 为直径,, 分别切 于点 ,.,则 的大小为
A. B. C. D.
8. 如图,在同一个圆中作出圆的内接正三角形 和正八边形 ,若连接 ,则 的度数是
A. B. C. D.
9. 如图, 的内切圆 与 ,, 分别相切于点 ,,,且 , 的周长为 ,则 的长为
A. B. C. D.
10. 下列命题中是真命题的有
①两个端点能够重合的弧是等弧;
②圆的任意一条弦把圆分成优弧和劣弧两部分;
③长度相等的弧是等弧;
④半径相等的圆是等圆;
⑤直径是最大的弦;
⑥半圆所对的弦是直径.
A. 3个 B. 4个 C. 5个 D. 6个
二、填空题(共10小题;共50分)
11. 的半径为 ,点 到直线 的距离为 ,当 时, 与 相切.
12. 如图,在 中,
()半径有: .
()直径有: .
()弦有: .
()劣弧 对应的优弧是 ,它们刚好拼成一个完整的圆.
13. 如图, 是 的直径,点 在 上,过点 的切线与 的延长线交于点 ,点 在 上(不与点 , 重合),连接 ,.若 ,则 度.
14. 以坐标原点 为圆心, 为半径作圆,若直线 与 相交,则 的取值范围是 .
15. 如图,点 是 的内心.
()若 ,则 的度数为 ;
()连接 ,则 (填“”“”或“”).
16. 如图,在 中,,若 ,则 .
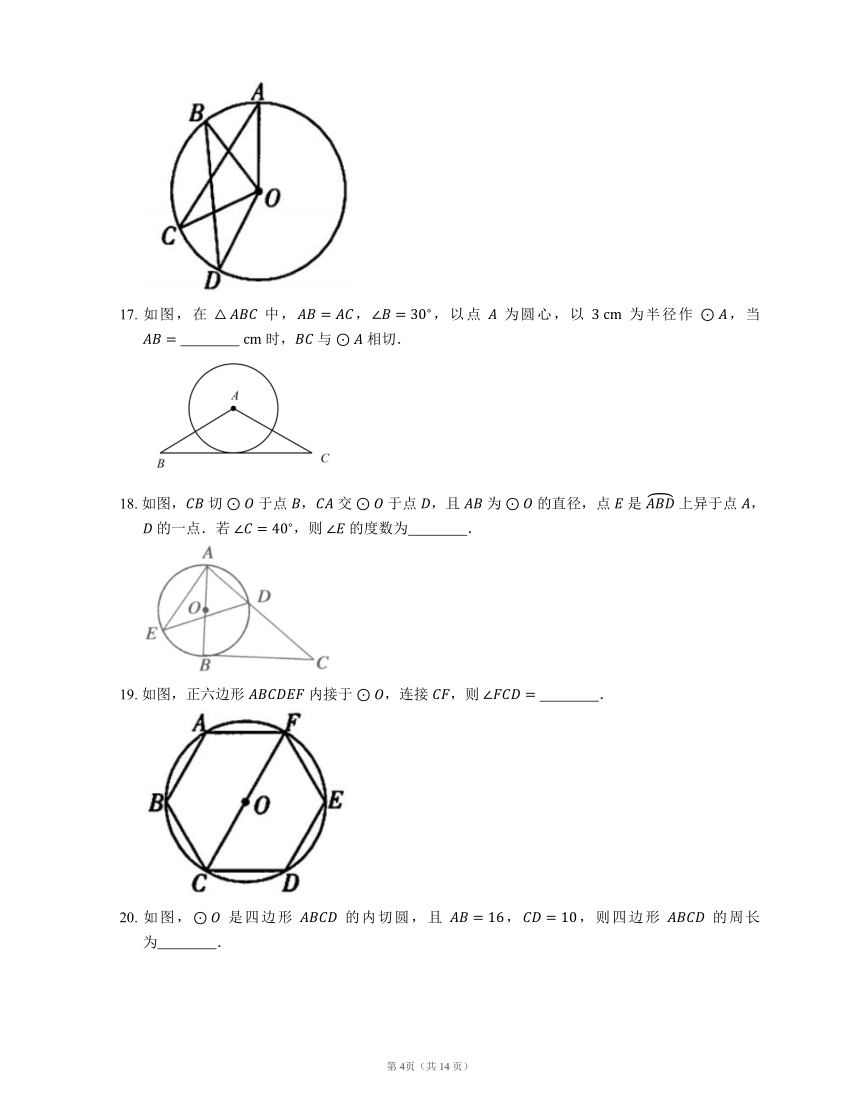
17. 如图,在 中,,,以点 为圆心,以 为半径作 ,当 时, 与 相切.
18. 如图, 切 于点 , 交 于点 ,且 为 的直径,点 是 上异于点 , 的一点.若 ,则 的度数为 .
19. 如图,正六边形 内接于 ,连接 ,则 .
20. 如图, 是四边形 的内切圆,且 ,,则四边形 的周长为 .
三、解答题(共6小题;共50分)
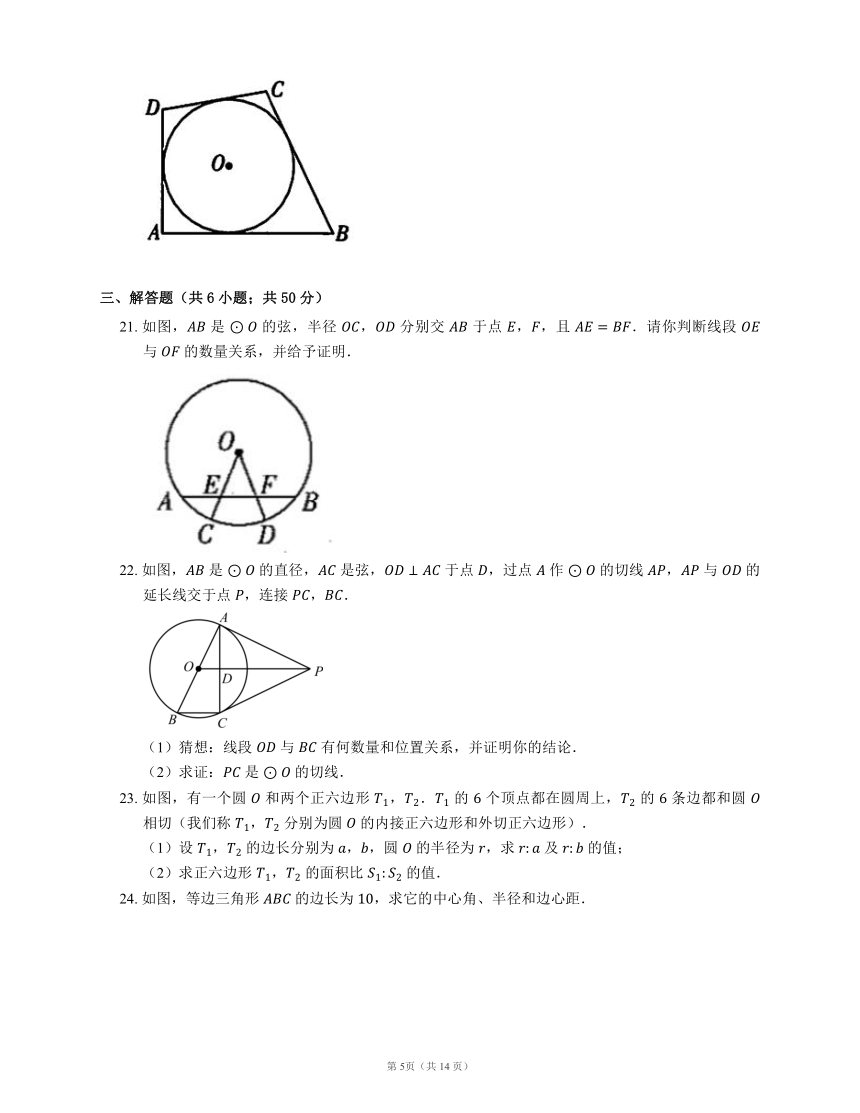
21. 如图, 是 的弦,半径 , 分别交 于点 ,,且 .请你判断线段 与 的数量关系,并给予证明.
22. 如图, 是 的直径, 是弦, 于点 ,过点 作 的切线 , 与 的延长线交于点 ,连接 ,.
(1)猜想:线段 与 有何数量和位置关系,并证明你的结论.
(2)求证: 是 的切线.
23. 如图,有一个圆 和两个正六边形 ,. 的 个顶点都在圆周上, 的 条边都和圆 相切(我们称 , 分别为圆 的内接正六边形和外切正六边形).
(1)设 , 的边长分别为 ,,圆 的半径为 ,求 及 的值;
(2)求正六边形 , 的面积比 的值.
24. 如图,等边三角形 的边长为 ,求它的中心角、半径和边心距.
25. 如图,,,, 是 上的点,,.
(1)求证:;
(2)能否求出 的长 若能,求出 的长;若不能,请说明理由.
26. 在 中,, 分别是 两边的中点,如果 上的所有点都在 的内部或边上,则称 为 的中内弧.例如,下图中 是 的一条中内弧.
(1)如图,在 中,,, 分别是 , 的中点.画出 的最长的中内弧 ,并直接写出此时 的长;
(2)在平面直角坐标系中,已知点 ,,,.在 中,, 分别是 , 的中点.
①若 ,求 的中内弧 所在圆的圆心 的纵坐标的取值范围;
②若在 中存在一条中内弧 ,使得 所在圆的圆心 在 的内部或边上,直接写出 的取值范围.
答案
第一部分
1. C
2. D
3. C 【解析】当点 在圆内时点 到点 的距离小于圆的半径,即:;
点 在圆上或圆外时点 到圆心的距离应该不小于圆的半径,即:;即 .
4. B
5. D
6. C
7. D 【解析】解法一:
切 于点 ,
,
又 ,
,
, 分别切 于点 ,,
,
,
.
解法二:如图,连接 ,
, 切 于 ,,
,
,,
,
.
8. A 【解析】如图,连接 ,,,.
正三角形的中心角 ,
正八边形的中心角 ,
,
,
.
9. C 【解析】 与 ,, 分别相切于点 ,,,
,,,
的周长为 ,
,
,
.
10. A
【解析】①能够完全重合的两条弧是等弧,故①错误;
②直径将圆分成两条相等的弧,故②错误;
③长度相等的两条弧不一定能完全重合,故③错误;
④只要半径相等的两圆一定是等圆,故④正确;
⑤直径是圆内最长的弦,故⑤正确;
⑥圆的直径将圆分成两个半圆,所以半圆所对的弦是直径,故⑥正确.
第二部分
11.
12. ,,,,,,
13.
【解析】如图,连接 ,
切 于 ,
,
,
,
的度数是 ,
优弧 的度数是 ,
.
14.
15. ,
16.
17.
【解析】过点 作 垂直于 于点 .
,
当 时,相切.
,
.
18.
【解析】如图,连接 .
由题意知 ,
,,
,
.
19.
20.
第三部分
21. .证明如下:
如图,连接 ,,
则 ,
,
又 ,
,
.
22. (1) 猜想:,.证明如下:
,
.
是 的直径,
.
是 的中位线,
,.
(2)
如图,连接 ,设 与 交于点 .
, 经过圆心 ,
,即 .
在 和 中,
,,
,
.
是 的切线,
.
,即 ,
是 的切线.
23. (1) 连接圆心 和 的 个顶点可得 个全等的正三角形.
所以 .
连接圆心 和 相邻的两个顶点,得以圆 半径高的正三角形,
所以 .
(2) 的边长比是 ,所以 .
24. 如图,
设等边三角形 的中心为点 ,过点 作 于点 ,连接 ,,则 ,,.
.
.
设 ,则 .
在 中,,
即 .
解得 (负值已舍去).
,.
等边三角形 的中心角为 ,半径为 ,边心距为 .
25. (1) ,
,
即 .
.
(2) ,
.
,
.
26. (1) 的最长的中内弧 ,如图.
的长为 .
(2) ①当 时,点 .
取 的中点 ,则四边形 为正方形.
(i)(除端点外)在线段 的上方,
当 所在 与 相切时,圆心 是正方形 的中心.
点 .
结合图形,可得点 的纵坐标 .
(ii)(除端点外)在线段 的下方,
当 所在圆 与 相切时,圆心 是线段 的中点.
点 .
结合图形,可得点 的纵坐标 .
综上所述,圆心 的纵坐标 的取值范围是 或 .
② 的取值范围是 .
【解析】如图 ,
当 (除端点外)在线段 上方,即 与 相切时, 易证 可求得 结合图象可知
如图 ,
当 (除端点外)在线段 下方,即 与 相切时,易证 可求得 ,设 与 交于点 ,
,进而在 中可求 ,结合图象可知 .综上, 的取值范围是 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 直线 与半径为 的 相交,且点 到直线 的距离为 ,则 的取值范围是
A. B. C. D.
2. 下列命题中正确的是
A. 垂直于半径的直线是圆的切线
B. 经过半径外端的直线是圆的切线
C. 经过切点的直线是圆的切线
D. 圆心到某直线的距离等于半径,那么这条直线是圆的切线
3. 已知 ,,,以点 为圆心 为半径作圆,如果点 、点 只有一个点在圆内,那么半径 的取值范围是
A. B. C. D.
4. 已知 的半径 , 的圆心到直线 的距离 ,则直线 与 的位置关系是
A. 相离 B. 相交 C. 相切 D. 无法确定
5. 下列命题中,正确的是
A. 平分一条直径的弦必垂直于这条直径
B. 平分一条弧的直线垂直于这条弧所对的弦
C. 弦的垂线必经过这条弦所在圆的圆心
D. 在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心
6. 如图, 为 的直径,点 , 是 的三等分点,,则 的度数为
A. B. C. D.
7. 如图, 中 为直径,, 分别切 于点 ,.,则 的大小为
A. B. C. D.
8. 如图,在同一个圆中作出圆的内接正三角形 和正八边形 ,若连接 ,则 的度数是
A. B. C. D.
9. 如图, 的内切圆 与 ,, 分别相切于点 ,,,且 , 的周长为 ,则 的长为
A. B. C. D.
10. 下列命题中是真命题的有
①两个端点能够重合的弧是等弧;
②圆的任意一条弦把圆分成优弧和劣弧两部分;
③长度相等的弧是等弧;
④半径相等的圆是等圆;
⑤直径是最大的弦;
⑥半圆所对的弦是直径.
A. 3个 B. 4个 C. 5个 D. 6个
二、填空题(共10小题;共50分)
11. 的半径为 ,点 到直线 的距离为 ,当 时, 与 相切.
12. 如图,在 中,
()半径有: .
()直径有: .
()弦有: .
()劣弧 对应的优弧是 ,它们刚好拼成一个完整的圆.
13. 如图, 是 的直径,点 在 上,过点 的切线与 的延长线交于点 ,点 在 上(不与点 , 重合),连接 ,.若 ,则 度.
14. 以坐标原点 为圆心, 为半径作圆,若直线 与 相交,则 的取值范围是 .
15. 如图,点 是 的内心.
()若 ,则 的度数为 ;
()连接 ,则 (填“”“”或“”).
16. 如图,在 中,,若 ,则 .
17. 如图,在 中,,,以点 为圆心,以 为半径作 ,当 时, 与 相切.
18. 如图, 切 于点 , 交 于点 ,且 为 的直径,点 是 上异于点 , 的一点.若 ,则 的度数为 .
19. 如图,正六边形 内接于 ,连接 ,则 .
20. 如图, 是四边形 的内切圆,且 ,,则四边形 的周长为 .
三、解答题(共6小题;共50分)
21. 如图, 是 的弦,半径 , 分别交 于点 ,,且 .请你判断线段 与 的数量关系,并给予证明.
22. 如图, 是 的直径, 是弦, 于点 ,过点 作 的切线 , 与 的延长线交于点 ,连接 ,.
(1)猜想:线段 与 有何数量和位置关系,并证明你的结论.
(2)求证: 是 的切线.
23. 如图,有一个圆 和两个正六边形 ,. 的 个顶点都在圆周上, 的 条边都和圆 相切(我们称 , 分别为圆 的内接正六边形和外切正六边形).
(1)设 , 的边长分别为 ,,圆 的半径为 ,求 及 的值;
(2)求正六边形 , 的面积比 的值.
24. 如图,等边三角形 的边长为 ,求它的中心角、半径和边心距.
25. 如图,,,, 是 上的点,,.
(1)求证:;
(2)能否求出 的长 若能,求出 的长;若不能,请说明理由.
26. 在 中,, 分别是 两边的中点,如果 上的所有点都在 的内部或边上,则称 为 的中内弧.例如,下图中 是 的一条中内弧.
(1)如图,在 中,,, 分别是 , 的中点.画出 的最长的中内弧 ,并直接写出此时 的长;
(2)在平面直角坐标系中,已知点 ,,,.在 中,, 分别是 , 的中点.
①若 ,求 的中内弧 所在圆的圆心 的纵坐标的取值范围;
②若在 中存在一条中内弧 ,使得 所在圆的圆心 在 的内部或边上,直接写出 的取值范围.
答案
第一部分
1. C
2. D
3. C 【解析】当点 在圆内时点 到点 的距离小于圆的半径,即:;
点 在圆上或圆外时点 到圆心的距离应该不小于圆的半径,即:;即 .
4. B
5. D
6. C
7. D 【解析】解法一:
切 于点 ,
,
又 ,
,
, 分别切 于点 ,,
,
,
.
解法二:如图,连接 ,
, 切 于 ,,
,
,,
,
.
8. A 【解析】如图,连接 ,,,.
正三角形的中心角 ,
正八边形的中心角 ,
,
,
.
9. C 【解析】 与 ,, 分别相切于点 ,,,
,,,
的周长为 ,
,
,
.
10. A
【解析】①能够完全重合的两条弧是等弧,故①错误;
②直径将圆分成两条相等的弧,故②错误;
③长度相等的两条弧不一定能完全重合,故③错误;
④只要半径相等的两圆一定是等圆,故④正确;
⑤直径是圆内最长的弦,故⑤正确;
⑥圆的直径将圆分成两个半圆,所以半圆所对的弦是直径,故⑥正确.
第二部分
11.
12. ,,,,,,
13.
【解析】如图,连接 ,
切 于 ,
,
,
,
的度数是 ,
优弧 的度数是 ,
.
14.
15. ,
16.
17.
【解析】过点 作 垂直于 于点 .
,
当 时,相切.
,
.
18.
【解析】如图,连接 .
由题意知 ,
,,
,
.
19.
20.
第三部分
21. .证明如下:
如图,连接 ,,
则 ,
,
又 ,
,
.
22. (1) 猜想:,.证明如下:
,
.
是 的直径,
.
是 的中位线,
,.
(2)
如图,连接 ,设 与 交于点 .
, 经过圆心 ,
,即 .
在 和 中,
,,
,
.
是 的切线,
.
,即 ,
是 的切线.
23. (1) 连接圆心 和 的 个顶点可得 个全等的正三角形.
所以 .
连接圆心 和 相邻的两个顶点,得以圆 半径高的正三角形,
所以 .
(2) 的边长比是 ,所以 .
24. 如图,
设等边三角形 的中心为点 ,过点 作 于点 ,连接 ,,则 ,,.
.
.
设 ,则 .
在 中,,
即 .
解得 (负值已舍去).
,.
等边三角形 的中心角为 ,半径为 ,边心距为 .
25. (1) ,
,
即 .
.
(2) ,
.
,
.
26. (1) 的最长的中内弧 ,如图.
的长为 .
(2) ①当 时,点 .
取 的中点 ,则四边形 为正方形.
(i)(除端点外)在线段 的上方,
当 所在 与 相切时,圆心 是正方形 的中心.
点 .
结合图形,可得点 的纵坐标 .
(ii)(除端点外)在线段 的下方,
当 所在圆 与 相切时,圆心 是线段 的中点.
点 .
结合图形,可得点 的纵坐标 .
综上所述,圆心 的纵坐标 的取值范围是 或 .
② 的取值范围是 .
【解析】如图 ,
当 (除端点外)在线段 上方,即 与 相切时, 易证 可求得 结合图象可知
如图 ,
当 (除端点外)在线段 下方,即 与 相切时,易证 可求得 ,设 与 交于点 ,
,进而在 中可求 ,结合图象可知 .综上, 的取值范围是 .
第1页(共1 页)
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
