北京课改版数学九年级第二十四章 投影、视图与展开图试卷(word解析版)
文档属性
| 名称 | 北京课改版数学九年级第二十四章 投影、视图与展开图试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 563.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 06:09:22 | ||
图片预览

文档简介
第二十四章 投影、视图与展开图
一、选择题(共10小题;共50分)
1. 下列几何体中,从正面看到的平面图形是圆的是
A. B.
C. D.
2. 圆柱的侧面展开图是
A. 圆形 B. 三角形 C. 梯形 D. 长方形
3. 下列说法正确的是
A. 皮影可看成平行投影
B. 无影灯(手术用的)是平行投影
C. 日食不是太阳光所形成的投影现象
D. 日食是太阳光所形成的投影现象
4. 如图是某个几何体的平面展开图,则这个几何体是
A. 长方体 B. 三棱柱 C. 四棱锥 D. 三棱锥
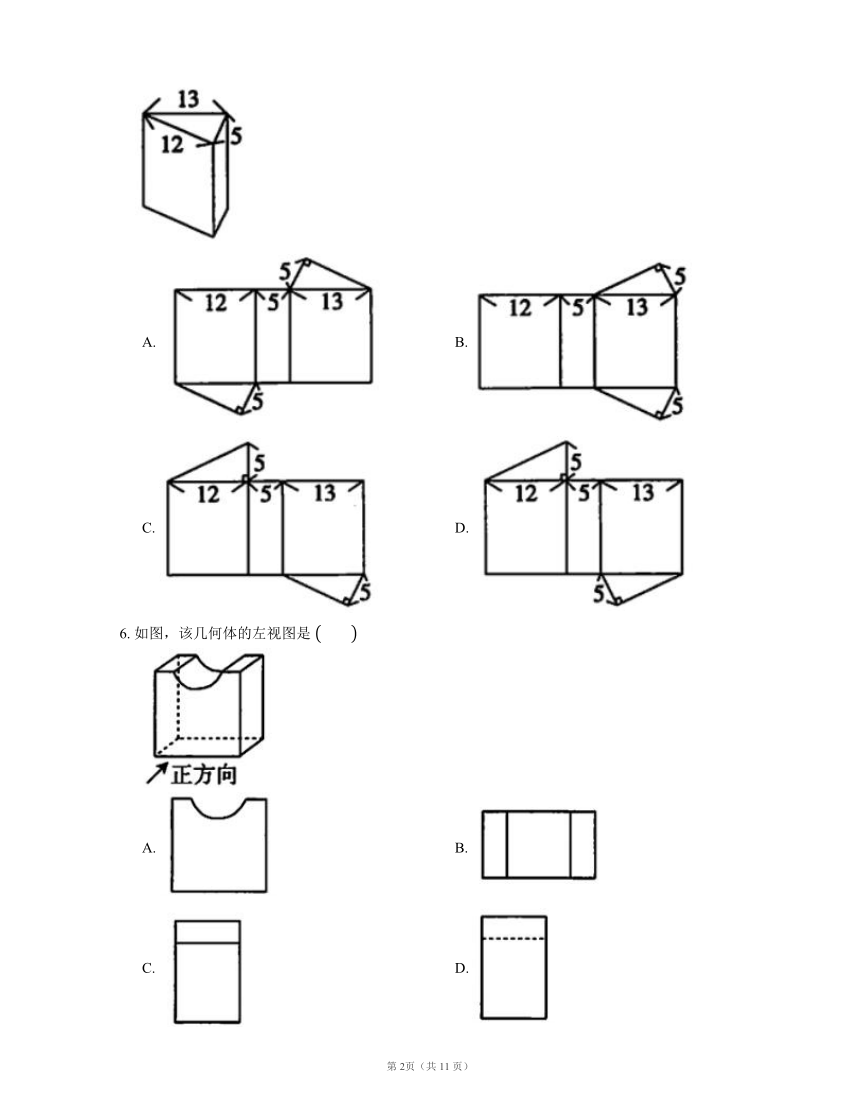
5. 如图为一直棱柱,其底面是三边长分别为 ,, 的直角三角形.若下列选项中的图形均由三个长方形与两个直角三角形组合而成,且其中一个为如图所示的直棱柱的展开图,则根据图形中标示的边长与直角符号判断,此展开图为
A. B.
C. D.
6. 如图,该几何体的左视图是
A. B.
C. D.
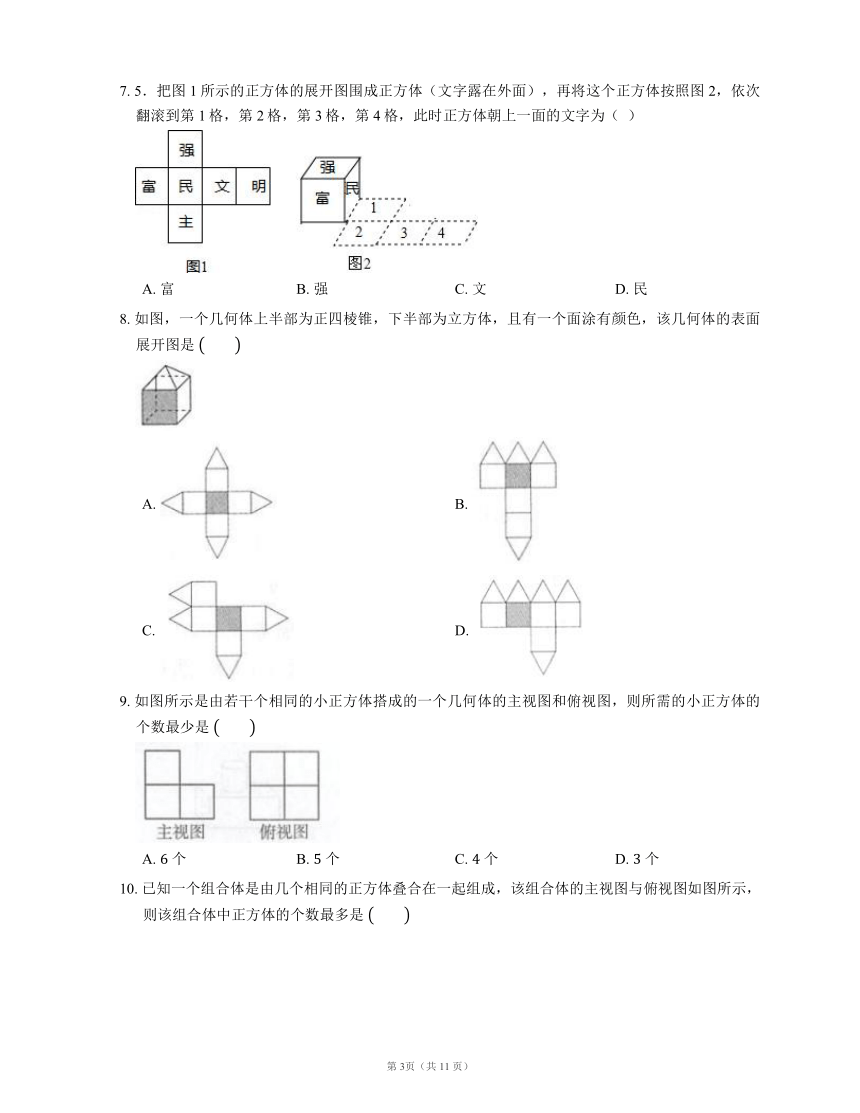
7. 5.把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为( )
A. 富 B. 强 C. 文 D. 民
8. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是
A. B.
C. D.
9. 如图所示是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图,则所需的小正方体的个数最少是
A. 个 B. 个 C. 个 D. 个
10. 已知一个组合体是由几个相同的正方体叠合在一起组成,该组合体的主视图与俯视图如图所示,则该组合体中正方体的个数最多是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 侧面展开图是长方形的简单几何体是 .
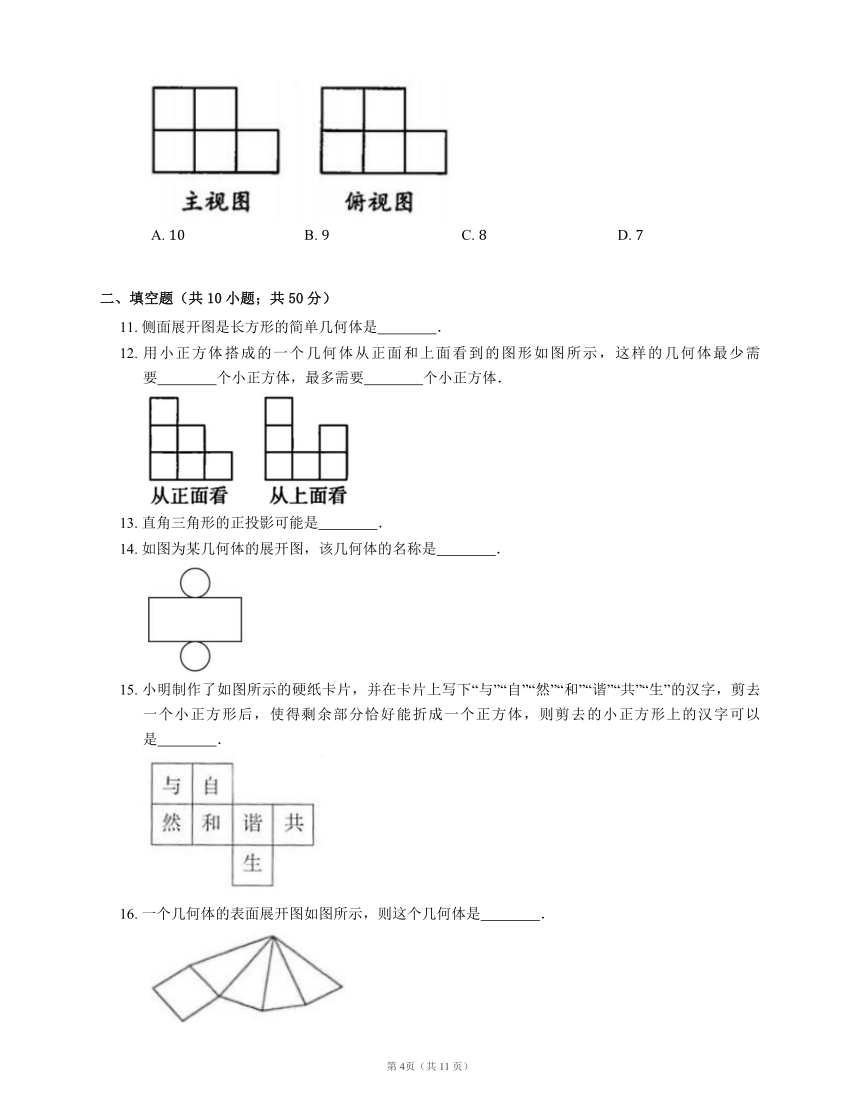
12. 用小正方体搭成的一个几何体从正面和上面看到的图形如图所示,这样的几何体最少需要 个小正方体,最多需要 个小正方体.
13. 直角三角形的正投影可能是 .
14. 如图为某几何体的展开图,该几何体的名称是 .
15. 小明制作了如图所示的硬纸卡片,并在卡片上写下“与”“自”“然”“和”“谐”“共”“生”的汉字,剪去一个小正方形后,使得剩余部分恰好能折成一个正方体,则剪去的小正方形上的汉字可以是 .
16. 一个几何体的表面展开图如图所示,则这个几何体是 .
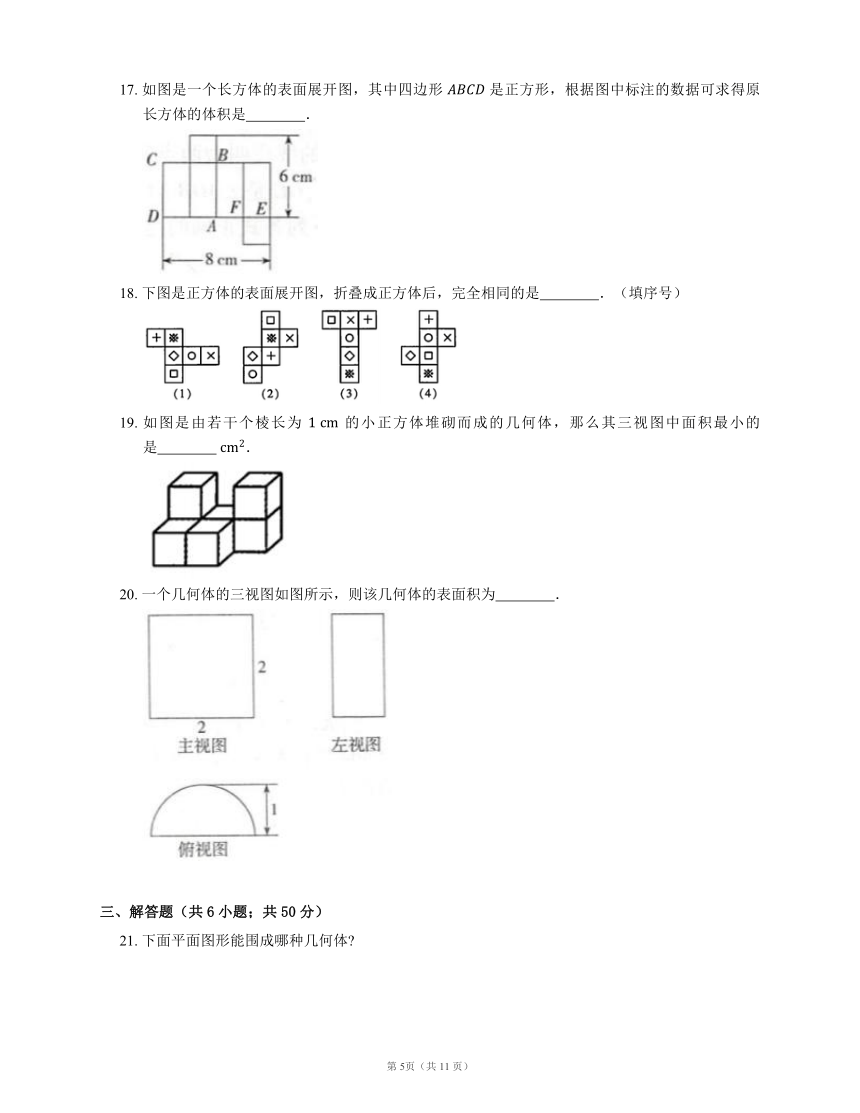
17. 如图是一个长方体的表面展开图,其中四边形 是正方形,根据图中标注的数据可求得原长方体的体积是 .
18. 下图是正方体的表面展开图,折叠成正方体后,完全相同的是 .(填序号)
19. 如图是由若干个棱长为 的小正方体堆砌而成的几何体,那么其三视图中面积最小的是 .
20. 一个几何体的三视图如图所示,则该几何体的表面积为 .
三、解答题(共6小题;共50分)
21. 下面平面图形能围成哪种几何体
22. 画出如图所示的物体从不同方向看到的平面图形.
(1)从上面看;
(2)从正面看;
(3)从左面看;
23. 如图,一只蚂蚁要从正方体纸箱的一个顶点 沿表面爬行到顶点 .
(1)画出正方体的一种展开图;(可适当调整大小)
(2)在展开图上画出蚂蚁爬行的最短路线;
(3)在原纸箱图上画出蚂蚁爬行的最短路线.(画一种即可)
24. 如图是某个月的日历,其中用实线框出的六个小正方形恰好是一个正方体的展开图.
(1)如果C所在方格内的数字是 ,那么A所在方格内的数字是几
(2)设A所在方格内的数字是 ,如果把此展开图折叠成原来的正方体,请用含 的代数式表示A相对的面的数字.
25. 如图,在方格纸中画出该几何体的三视图.
26. 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为 的小明 的影子 长是 ,而小颖 刚好在路灯灯泡的正下方 点,并测得 .
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置 ;
(2)求路灯灯泡的垂直高度 ;
(3)如果小明沿线段 向小颖(点 )走去,当小明走到 中点 处时,求其影子 的长;当小明继续走剩下路程的 到 处时,求其影子 的长;当小明继续走剩下路程的 到 处, 按此规律继续走下去,当小明走剩下路程的 到 处时,求影子 的长(直接用 的代数式表示).
答案
第一部分
1. C
2. D
3. D 【解析】皮影是灯光下产生的影子是中心投影;无影灯是多个点光源组成的,不是平行投影;当月球运行到地球与太阳之间三者在一条直线上时,月球就会挡住太阳射向地球的光,月球身后的黑影正好落在地球上,这时发生日食现象.
4. C
5. D
【解析】A选项中,展开图下方的直角三角形的斜边长为 ,不合题意;B选项中,展开图上下两个直角三角形的直角边不能与对应的棱完全重合,不合题意;C选项中,展开图下方的直角三角形的直角边不能与对应的棱完全重合,不合题意;D选项中,展开图能折叠成一个如题图所示的直棱柱,符合题意.
6. D
7. A 【解析】由图1可得,“富”和“文”相对;“强”和“主”相对;“民”和“明”相对;
由图2可得,小正方体从图2的位置依次翻到第4格时,“文”在下面,则这时小正方体朝上面的字是“富”,
故选:A.
8. B 【解析】选项A和C中涂有颜色的一个面是底面,不能折叠成题图中的几何体;选项B能折叠成题图中的几何体;D选项中有 个三角形,故不是这个几何体的表面展开图.
9. B
10. B
第二部分
11. 圆柱或直棱柱
12. ,
13. 三角形或线段
14. 圆柱
15. “与”或“自”或“然”
【解析】因为剩余的部分恰好能折成一个正方体,所以展开图中没有“田”字形,所以应剪去写有“与“或”自”或“然”的小正方形.
16. 四棱锥
17.
【解析】解析
因为四边形 是正方形,
所以 ,
令长方体的高为 ,
则 ,
所以原长方体的体积是 .
18. ()()
【解析】() 对面是 , 对面是 , 对面是 .
() 对面是 , 对面是 , 对面是 .若以 为正面,以 为上面,则 .
() 对面是 , 对面是 , 对面是 .若以 为正面,以 为上面,则 .
() 对面是 , 对面是 , 对面是 .若以 为正面,以 为上面,则 .
观察可知折叠成正方体后,完全相同的是()().
19.
【解析】主视图是,面积是 ;
左视图是,面积是 ;
俯视图是,面积是 .
20.
【解析】观察该几何体的三视图发现其为半圆柱,半圆柱的底面圆直径为 ,高为 ,故其表面积为 .
第三部分
21. 圆锥.
22. (1)
(2)
(3)
23. (1) 画展开图如答图 所示.
(2) 如答图 ,连接 , 即是蚂蚁爬行的最短路线.
(3) 如答图 ,折线 即为所求.(答案不唯一)
24. (1) 因为C所在方格内的数字是 ,所以D所在方格内的数字是 ,A所在方格内的数字为 .
(2) A相对的面是F,A所在方格内的数字为 ,D所在方格内的数字为 ,C所点方格内的数字为 ,F所在方格内的数字为 .
25. 画该几何体的三视图如图所示.
26. (1)
(2) 由题意得 ,
所以 ,
即 ,
所以 .
(3)
由题意得 ,
所以 ,
即 ,
所以 ;
同理可得 ;
以此类推,可得 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 下列几何体中,从正面看到的平面图形是圆的是
A. B.
C. D.
2. 圆柱的侧面展开图是
A. 圆形 B. 三角形 C. 梯形 D. 长方形
3. 下列说法正确的是
A. 皮影可看成平行投影
B. 无影灯(手术用的)是平行投影
C. 日食不是太阳光所形成的投影现象
D. 日食是太阳光所形成的投影现象
4. 如图是某个几何体的平面展开图,则这个几何体是
A. 长方体 B. 三棱柱 C. 四棱锥 D. 三棱锥
5. 如图为一直棱柱,其底面是三边长分别为 ,, 的直角三角形.若下列选项中的图形均由三个长方形与两个直角三角形组合而成,且其中一个为如图所示的直棱柱的展开图,则根据图形中标示的边长与直角符号判断,此展开图为
A. B.
C. D.
6. 如图,该几何体的左视图是
A. B.
C. D.
7. 5.把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为( )
A. 富 B. 强 C. 文 D. 民
8. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是
A. B.
C. D.
9. 如图所示是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图,则所需的小正方体的个数最少是
A. 个 B. 个 C. 个 D. 个
10. 已知一个组合体是由几个相同的正方体叠合在一起组成,该组合体的主视图与俯视图如图所示,则该组合体中正方体的个数最多是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 侧面展开图是长方形的简单几何体是 .
12. 用小正方体搭成的一个几何体从正面和上面看到的图形如图所示,这样的几何体最少需要 个小正方体,最多需要 个小正方体.
13. 直角三角形的正投影可能是 .
14. 如图为某几何体的展开图,该几何体的名称是 .
15. 小明制作了如图所示的硬纸卡片,并在卡片上写下“与”“自”“然”“和”“谐”“共”“生”的汉字,剪去一个小正方形后,使得剩余部分恰好能折成一个正方体,则剪去的小正方形上的汉字可以是 .
16. 一个几何体的表面展开图如图所示,则这个几何体是 .
17. 如图是一个长方体的表面展开图,其中四边形 是正方形,根据图中标注的数据可求得原长方体的体积是 .
18. 下图是正方体的表面展开图,折叠成正方体后,完全相同的是 .(填序号)
19. 如图是由若干个棱长为 的小正方体堆砌而成的几何体,那么其三视图中面积最小的是 .
20. 一个几何体的三视图如图所示,则该几何体的表面积为 .
三、解答题(共6小题;共50分)
21. 下面平面图形能围成哪种几何体
22. 画出如图所示的物体从不同方向看到的平面图形.
(1)从上面看;
(2)从正面看;
(3)从左面看;
23. 如图,一只蚂蚁要从正方体纸箱的一个顶点 沿表面爬行到顶点 .
(1)画出正方体的一种展开图;(可适当调整大小)
(2)在展开图上画出蚂蚁爬行的最短路线;
(3)在原纸箱图上画出蚂蚁爬行的最短路线.(画一种即可)
24. 如图是某个月的日历,其中用实线框出的六个小正方形恰好是一个正方体的展开图.
(1)如果C所在方格内的数字是 ,那么A所在方格内的数字是几
(2)设A所在方格内的数字是 ,如果把此展开图折叠成原来的正方体,请用含 的代数式表示A相对的面的数字.
25. 如图,在方格纸中画出该几何体的三视图.
26. 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为 的小明 的影子 长是 ,而小颖 刚好在路灯灯泡的正下方 点,并测得 .
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置 ;
(2)求路灯灯泡的垂直高度 ;
(3)如果小明沿线段 向小颖(点 )走去,当小明走到 中点 处时,求其影子 的长;当小明继续走剩下路程的 到 处时,求其影子 的长;当小明继续走剩下路程的 到 处, 按此规律继续走下去,当小明走剩下路程的 到 处时,求影子 的长(直接用 的代数式表示).
答案
第一部分
1. C
2. D
3. D 【解析】皮影是灯光下产生的影子是中心投影;无影灯是多个点光源组成的,不是平行投影;当月球运行到地球与太阳之间三者在一条直线上时,月球就会挡住太阳射向地球的光,月球身后的黑影正好落在地球上,这时发生日食现象.
4. C
5. D
【解析】A选项中,展开图下方的直角三角形的斜边长为 ,不合题意;B选项中,展开图上下两个直角三角形的直角边不能与对应的棱完全重合,不合题意;C选项中,展开图下方的直角三角形的直角边不能与对应的棱完全重合,不合题意;D选项中,展开图能折叠成一个如题图所示的直棱柱,符合题意.
6. D
7. A 【解析】由图1可得,“富”和“文”相对;“强”和“主”相对;“民”和“明”相对;
由图2可得,小正方体从图2的位置依次翻到第4格时,“文”在下面,则这时小正方体朝上面的字是“富”,
故选:A.
8. B 【解析】选项A和C中涂有颜色的一个面是底面,不能折叠成题图中的几何体;选项B能折叠成题图中的几何体;D选项中有 个三角形,故不是这个几何体的表面展开图.
9. B
10. B
第二部分
11. 圆柱或直棱柱
12. ,
13. 三角形或线段
14. 圆柱
15. “与”或“自”或“然”
【解析】因为剩余的部分恰好能折成一个正方体,所以展开图中没有“田”字形,所以应剪去写有“与“或”自”或“然”的小正方形.
16. 四棱锥
17.
【解析】解析
因为四边形 是正方形,
所以 ,
令长方体的高为 ,
则 ,
所以原长方体的体积是 .
18. ()()
【解析】() 对面是 , 对面是 , 对面是 .
() 对面是 , 对面是 , 对面是 .若以 为正面,以 为上面,则 .
() 对面是 , 对面是 , 对面是 .若以 为正面,以 为上面,则 .
() 对面是 , 对面是 , 对面是 .若以 为正面,以 为上面,则 .
观察可知折叠成正方体后,完全相同的是()().
19.
【解析】主视图是,面积是 ;
左视图是,面积是 ;
俯视图是,面积是 .
20.
【解析】观察该几何体的三视图发现其为半圆柱,半圆柱的底面圆直径为 ,高为 ,故其表面积为 .
第三部分
21. 圆锥.
22. (1)
(2)
(3)
23. (1) 画展开图如答图 所示.
(2) 如答图 ,连接 , 即是蚂蚁爬行的最短路线.
(3) 如答图 ,折线 即为所求.(答案不唯一)
24. (1) 因为C所在方格内的数字是 ,所以D所在方格内的数字是 ,A所在方格内的数字为 .
(2) A相对的面是F,A所在方格内的数字为 ,D所在方格内的数字为 ,C所点方格内的数字为 ,F所在方格内的数字为 .
25. 画该几何体的三视图如图所示.
26. (1)
(2) 由题意得 ,
所以 ,
即 ,
所以 .
(3)
由题意得 ,
所以 ,
即 ,
所以 ;
同理可得 ;
以此类推,可得 .
第1页(共1 页)
