北京课改版数学九年级第第二十五章概率的求法与应用期末测试试卷(word解析版)
文档属性
| 名称 | 北京课改版数学九年级第第二十五章概率的求法与应用期末测试试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 226.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 06:11:51 | ||
图片预览



文档简介
第二十五章 概率的求法与应用
一、选择题(共10小题;共50分)
1. 一个不透明的口袋中装有 个完全相同的小球,把它们分别标号为 ,,,,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于 的概率为
A. B. C. D.
2. 小红在解一道 选 的选择题时,由于她不会做,于是就猜了一个答案,则小红本题答对的可能性大小是
A. B. C. D.
3. 从 ,,, 这四个数中任取两个不同的数,则这两个数之和小于 的概率为
A. B. C. D.
4. 把一个圆盘 等分,指针落在某一个区域的可能性是
A. B. C. D.
5. 在一个不透明的布袋中装有 个白球和若干个黑球,它们除颜色外其它都相同,小明每次摸出一个球记录下颜色后放回并摇匀,通过多次试验发现,摸到黑球的频率稳定在 左右,则布袋中黑球的个数最可能是
A. 个 B. 个 C. 个 D. 个
6. 经过某个十字路口的汽车,可能直行,也可能左转或者右转,假设这 种可能性相同,现有两辆汽车经过这个十字路口,驶向相同方向的概率是
A. B. C. D.
7. 小玲在一次班会中参与知识抢答活动,现有语文题 道,数学题 道,综合题 道,她从中随机抽取 道,抽中数学题的概率是
A. B. C. D.
8. 九()班从小华、小琪、小明、小伟四人中随机抽出 人参加学校举行的乒乓球双打比赛,每人被抽到的可能性相等,则恰好抽到小华和小明的概率是
A. B. C. D.
9. 有四个一模一样的小球,其中三个小球上面分别标有数字 ,,,小明和小亮各摸一个,前一个人随机摸一个小球记下数字后放回,混合均匀,后一个人再随机摸一个小球,如果两人摸得小球的数字之和为 的概率为 ,那么第四个小球上的数字是
A. B. C. 或 D.
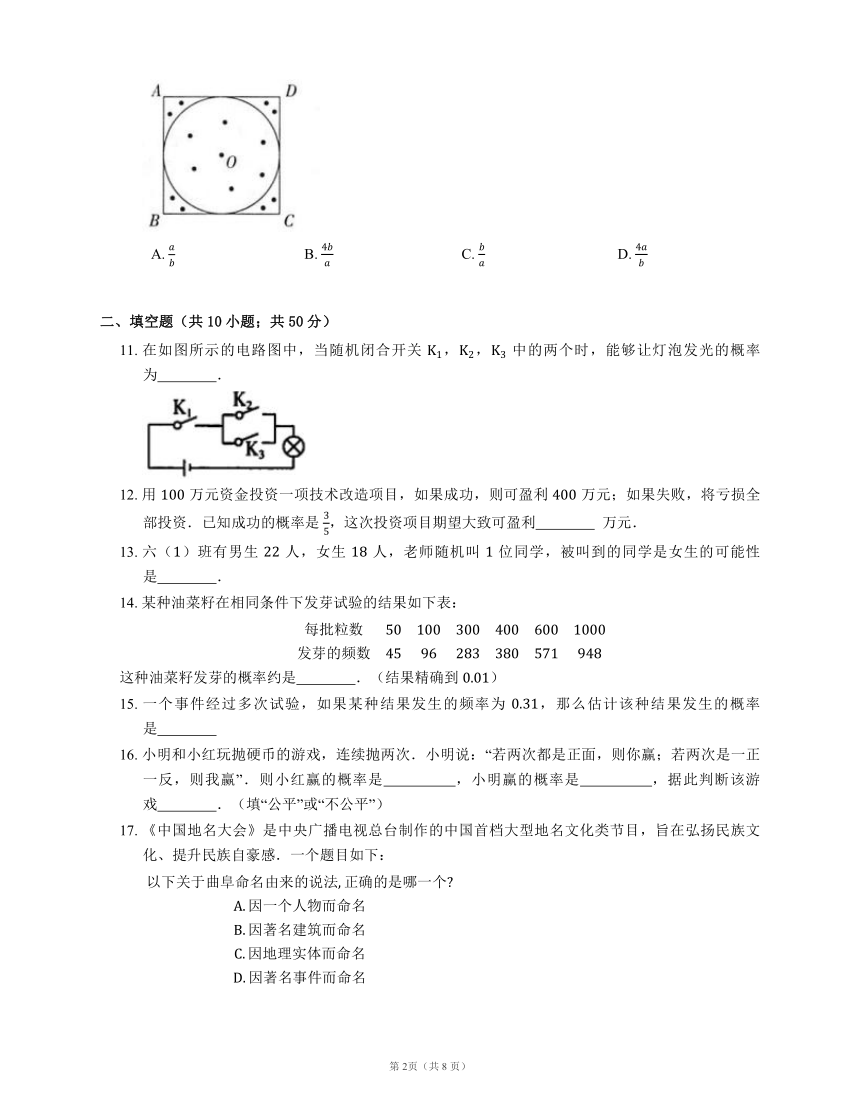
10. 如图,正方形 内有一个圆 .电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数 ,圆 内的点数 (在正方形边上和圆上的点不在统计中),利用频率估计概率的原理,可推得 的大小是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 在如图所示的电路图中,当随机闭合开关 ,, 中的两个时,能够让灯泡发光的概率为 .
12. 用 万元资金投资一项技术改造项目,如果成功,则可盈利 万元;如果失败,将亏损全部投资.已知成功的概率是 ,这次投资项目期望大致可盈利 万元.
13. 六()班有男生 人,女生 人,老师随机叫 位同学,被叫到的同学是女生的可能性是 .
14. 某种油菜籽在相同条件下发芽试验的结果如下表:
这种油菜籽发芽的概率约是 .(结果精确到 )
15. 一个事件经过多次试验,如果某种结果发生的频率为 ,那么估计该种结果发生的概率是
16. 小明和小红玩抛硬币的游戏,连续抛两次.小明说:“若两次都是正面,则你赢;若两次是一正一反,则我赢”.则小红赢的概率是 ,小明赢的概率是 ,据此判断该游戏 .(填“公平”或“不公平”)
17. 《中国地名大会》是中央广播电视总台制作的中国首档大型地名文化类节目,旨在弘扬民族文化、提升民族自豪感.一个题目如下:
甲、乙两名同学都不会这个题目,就随机选择一个答案,他们选取的答案恰好都是正确答案 的概率为 .
18. 在一个不透明的袋子中只装有 个白球和 个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是 .若再放入 个红球,摸到红球的概率变为 ,那么 的值为 .
19. 如图,五一黄金周期间,某景区规定 , 为入口,,, 为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从 入口进入,从 或 出口离开的概率是 .
20. 现有四张分别标有数字 ,,, 的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是 .
三、解答题(共6小题;共50分)
21. 某校开展科技节展览活动,设置了编号为 号的四个展区,小佳计划随机参观两个展区,且每个展区被选中的机会均等,求 号展区被选中的概率.
22. 经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
23. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成 份),并规定:顾客每购物满 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得 元、 元、 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得 元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更合算 请说明理由.
24. 某种密码锁有三个转轮,每个转轮上有十个数字:,,,,.小黄同学是 月份中旬出生的,他用生日“月份 日期”设置密码:(注:中旬为某月中的 日),小张同学要破解其密码:
(1)第一个转轮设置的数字是 ,第二个转轮设置的数字可能是 ;
(2)请你帮小张同学列举出所有可能的密码,并求密码数能被 整除的概率.
25. 对某批乒乓球质量进行随机调查的结果如下表:
(1)将表格补充完整;
(2)根据上表估计,在这批乒乓球中任取一个球,是优等品的概率是 ;(保留两位小数)
(3)学校需要 个优等品乒乓球,试估计购进多少个乒乓球最合适 (结果保留整数)
26. 在一个口袋中装有 个完全相同的小球,把它们分别标号为 ,,,随机摸出一个小球后放回,再随机摸出一个小球,将两次摸出小球的标号相加.
(1)将所有的结果填入下表:
(2)求两次摸出小球的标号和等于 的概率
答案
第一部分
1. A 【解析】画树状图,得
共有 种等可能的结果,两次摸出的小球标号之和等于 的有 种结果,
两次摸出的小球标号之和等于 的概率 .
2. A
3. C
4. C
5. A
6. A
7. C
8. C 【解析】把小华、小琪、小明、小伟分别记为 ,,,,列表如下:
共有 个等可能的结果,恰好抽到小华和小明的结果有 个,
恰好抽到小华和小明的概率为 .
9. C 【解析】设第四个小球上的数字为 ,画树状图如下:
共有 种等可能的结果,而两人摸得小球的数字之和为 的概率为 ,则两人摸得小球的数字之和为 的结果有 种.分析树状图知 ,当 时不符合,当 时,,,符合;当 时,,,符合,所以第四个小球上的数字为 或 .故选C.
10. B
【解析】设圆的半径为 ,则正方形的边长为 ,
根据题意得 ,
故 .
第二部分
11.
12.
【解析】(万元)
13.
14.
15.
16. ,,不公平
17.
【解析】列表如下:
由表格可知,共有 种等可能的结果,其中两人都选择 的结果有 种,
所以他们选取的答案恰好都是正确答案 的概率为 .
18.
【解析】根据题意得
解得 ,,
经检验 , 是这个方程组的解,
所以 .
19.
20.
第三部分
21. 列表如下:
由表格可知,共有 种等可能的结果,其中 号展厅被选中的结果有 种,
号展区被选中的概率为 .
22. (1) .
(2) .
(3) .
23. 根据题意得:转转盘所获得的购物券为:
因为 ,
所以选择转转盘对顾客更合算.
24. (1) 或
(2) 所有可能的密码是 ,,,,,,,,,,共有 种等可能的结果,其中能被 整除的有 ,, 共 种.
密码数能被 整除的概率为 .
25. (1)
(2)
(3) 设购进 个乒乓球最合适.
根据题意,得
解得
答:估计购进 个乒乓球最合适.
26. (1)
(2) 由表格可知,共有 种等可能的结果,其中两次摸出小球的标号和等于 的结果有 种,
两次摸出小球的标号和等于 的概率为 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 一个不透明的口袋中装有 个完全相同的小球,把它们分别标号为 ,,,,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于 的概率为
A. B. C. D.
2. 小红在解一道 选 的选择题时,由于她不会做,于是就猜了一个答案,则小红本题答对的可能性大小是
A. B. C. D.
3. 从 ,,, 这四个数中任取两个不同的数,则这两个数之和小于 的概率为
A. B. C. D.
4. 把一个圆盘 等分,指针落在某一个区域的可能性是
A. B. C. D.
5. 在一个不透明的布袋中装有 个白球和若干个黑球,它们除颜色外其它都相同,小明每次摸出一个球记录下颜色后放回并摇匀,通过多次试验发现,摸到黑球的频率稳定在 左右,则布袋中黑球的个数最可能是
A. 个 B. 个 C. 个 D. 个
6. 经过某个十字路口的汽车,可能直行,也可能左转或者右转,假设这 种可能性相同,现有两辆汽车经过这个十字路口,驶向相同方向的概率是
A. B. C. D.
7. 小玲在一次班会中参与知识抢答活动,现有语文题 道,数学题 道,综合题 道,她从中随机抽取 道,抽中数学题的概率是
A. B. C. D.
8. 九()班从小华、小琪、小明、小伟四人中随机抽出 人参加学校举行的乒乓球双打比赛,每人被抽到的可能性相等,则恰好抽到小华和小明的概率是
A. B. C. D.
9. 有四个一模一样的小球,其中三个小球上面分别标有数字 ,,,小明和小亮各摸一个,前一个人随机摸一个小球记下数字后放回,混合均匀,后一个人再随机摸一个小球,如果两人摸得小球的数字之和为 的概率为 ,那么第四个小球上的数字是
A. B. C. 或 D.
10. 如图,正方形 内有一个圆 .电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数 ,圆 内的点数 (在正方形边上和圆上的点不在统计中),利用频率估计概率的原理,可推得 的大小是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 在如图所示的电路图中,当随机闭合开关 ,, 中的两个时,能够让灯泡发光的概率为 .
12. 用 万元资金投资一项技术改造项目,如果成功,则可盈利 万元;如果失败,将亏损全部投资.已知成功的概率是 ,这次投资项目期望大致可盈利 万元.
13. 六()班有男生 人,女生 人,老师随机叫 位同学,被叫到的同学是女生的可能性是 .
14. 某种油菜籽在相同条件下发芽试验的结果如下表:
这种油菜籽发芽的概率约是 .(结果精确到 )
15. 一个事件经过多次试验,如果某种结果发生的频率为 ,那么估计该种结果发生的概率是
16. 小明和小红玩抛硬币的游戏,连续抛两次.小明说:“若两次都是正面,则你赢;若两次是一正一反,则我赢”.则小红赢的概率是 ,小明赢的概率是 ,据此判断该游戏 .(填“公平”或“不公平”)
17. 《中国地名大会》是中央广播电视总台制作的中国首档大型地名文化类节目,旨在弘扬民族文化、提升民族自豪感.一个题目如下:
甲、乙两名同学都不会这个题目,就随机选择一个答案,他们选取的答案恰好都是正确答案 的概率为 .
18. 在一个不透明的袋子中只装有 个白球和 个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是 .若再放入 个红球,摸到红球的概率变为 ,那么 的值为 .
19. 如图,五一黄金周期间,某景区规定 , 为入口,,, 为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从 入口进入,从 或 出口离开的概率是 .
20. 现有四张分别标有数字 ,,, 的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的卡片所标数字不同的概率是 .
三、解答题(共6小题;共50分)
21. 某校开展科技节展览活动,设置了编号为 号的四个展区,小佳计划随机参观两个展区,且每个展区被选中的机会均等,求 号展区被选中的概率.
22. 经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
23. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成 份),并规定:顾客每购物满 元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得 元、 元、 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得 元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更合算 请说明理由.
24. 某种密码锁有三个转轮,每个转轮上有十个数字:,,,,.小黄同学是 月份中旬出生的,他用生日“月份 日期”设置密码:(注:中旬为某月中的 日),小张同学要破解其密码:
(1)第一个转轮设置的数字是 ,第二个转轮设置的数字可能是 ;
(2)请你帮小张同学列举出所有可能的密码,并求密码数能被 整除的概率.
25. 对某批乒乓球质量进行随机调查的结果如下表:
(1)将表格补充完整;
(2)根据上表估计,在这批乒乓球中任取一个球,是优等品的概率是 ;(保留两位小数)
(3)学校需要 个优等品乒乓球,试估计购进多少个乒乓球最合适 (结果保留整数)
26. 在一个口袋中装有 个完全相同的小球,把它们分别标号为 ,,,随机摸出一个小球后放回,再随机摸出一个小球,将两次摸出小球的标号相加.
(1)将所有的结果填入下表:
(2)求两次摸出小球的标号和等于 的概率
答案
第一部分
1. A 【解析】画树状图,得
共有 种等可能的结果,两次摸出的小球标号之和等于 的有 种结果,
两次摸出的小球标号之和等于 的概率 .
2. A
3. C
4. C
5. A
6. A
7. C
8. C 【解析】把小华、小琪、小明、小伟分别记为 ,,,,列表如下:
共有 个等可能的结果,恰好抽到小华和小明的结果有 个,
恰好抽到小华和小明的概率为 .
9. C 【解析】设第四个小球上的数字为 ,画树状图如下:
共有 种等可能的结果,而两人摸得小球的数字之和为 的概率为 ,则两人摸得小球的数字之和为 的结果有 种.分析树状图知 ,当 时不符合,当 时,,,符合;当 时,,,符合,所以第四个小球上的数字为 或 .故选C.
10. B
【解析】设圆的半径为 ,则正方形的边长为 ,
根据题意得 ,
故 .
第二部分
11.
12.
【解析】(万元)
13.
14.
15.
16. ,,不公平
17.
【解析】列表如下:
由表格可知,共有 种等可能的结果,其中两人都选择 的结果有 种,
所以他们选取的答案恰好都是正确答案 的概率为 .
18.
【解析】根据题意得
解得 ,,
经检验 , 是这个方程组的解,
所以 .
19.
20.
第三部分
21. 列表如下:
由表格可知,共有 种等可能的结果,其中 号展厅被选中的结果有 种,
号展区被选中的概率为 .
22. (1) .
(2) .
(3) .
23. 根据题意得:转转盘所获得的购物券为:
因为 ,
所以选择转转盘对顾客更合算.
24. (1) 或
(2) 所有可能的密码是 ,,,,,,,,,,共有 种等可能的结果,其中能被 整除的有 ,, 共 种.
密码数能被 整除的概率为 .
25. (1)
(2)
(3) 设购进 个乒乓球最合适.
根据题意,得
解得
答:估计购进 个乒乓球最合适.
26. (1)
(2) 由表格可知,共有 种等可能的结果,其中两次摸出小球的标号和等于 的结果有 种,
两次摸出小球的标号和等于 的概率为 .
第1页(共1 页)
