北京课改版数学九年级第二十六章综合运用数学知识解决实际问题试卷(word解析版)
文档属性
| 名称 | 北京课改版数学九年级第二十六章综合运用数学知识解决实际问题试卷(word解析版) | 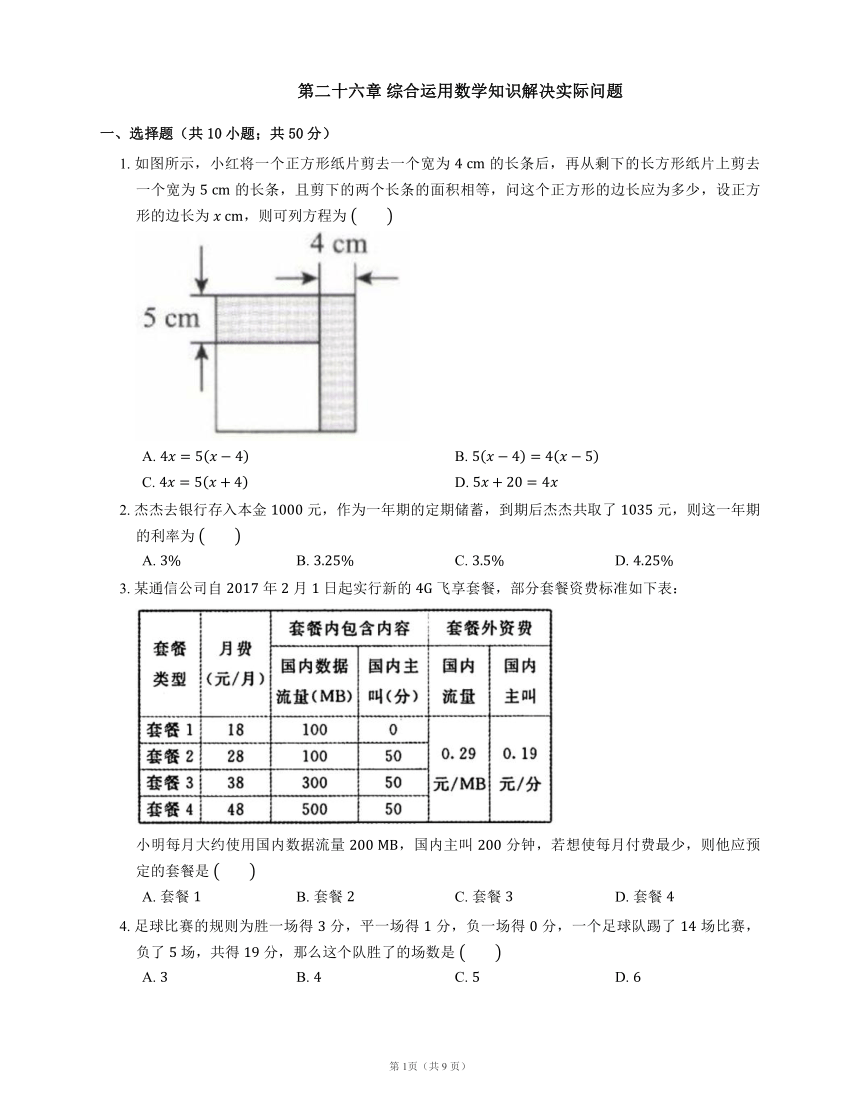 | |
| 格式 | zip | ||
| 文件大小 | 413.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 06:13:49 | ||
图片预览



文档简介
第二十六章 综合运用数学知识解决实际问题
一、选择题(共10小题;共50分)
1. 如图所示,小红将一个正方形纸片剪去一个宽为 的长条后,再从剩下的长方形纸片上剪去一个宽为 的长条,且剪下的两个长条的面积相等,问这个正方形的边长应为多少,设正方形的边长为 ,则可列方程为
A. B.
C. D.
2. 杰杰去银行存入本金 元,作为一年期的定期储蓄,到期后杰杰共取了 元,则这一年期的利率为
A. B. C. D.
3. 某通信公司自 年 月 日起实行新的 飞享套餐,部分套餐资费标准如下表:
小明每月大约使用国内数据流量 ,国内主叫 分钟,若想使每月付费最少,则他应预定的套餐是
A. 套餐 B. 套餐 C. 套餐 D. 套餐
4. 足球比赛的规则为胜一场得 分,平一场得 分,负一场得 分,一个足球队踢了 场比赛,负了 场,共得 分,那么这个队胜了的场数是
A. B. C. D.
5. 小明早上从家骑自行车去上学,先走平路到达点 ,再走上坡路到达点 ,最后走下坡路到达学校,小明骑自行车所走的路程 (单位:千米)与他所用的时间 (单位:分钟)的关系如图所示,放学后,小明沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,下列说法:
①小明家距学校 千米;
②小明上学所用的时间为 分钟;
③小明上坡的速度是 千米/分钟;
④小明放学回家所用时间为 分钟.
其中正确的个数是
A. 个 B. 个 C. 个 D. 个
6. 如图是某月的月历,横着取连续的三个数字,它们的和不可能是
A. B. C. D.
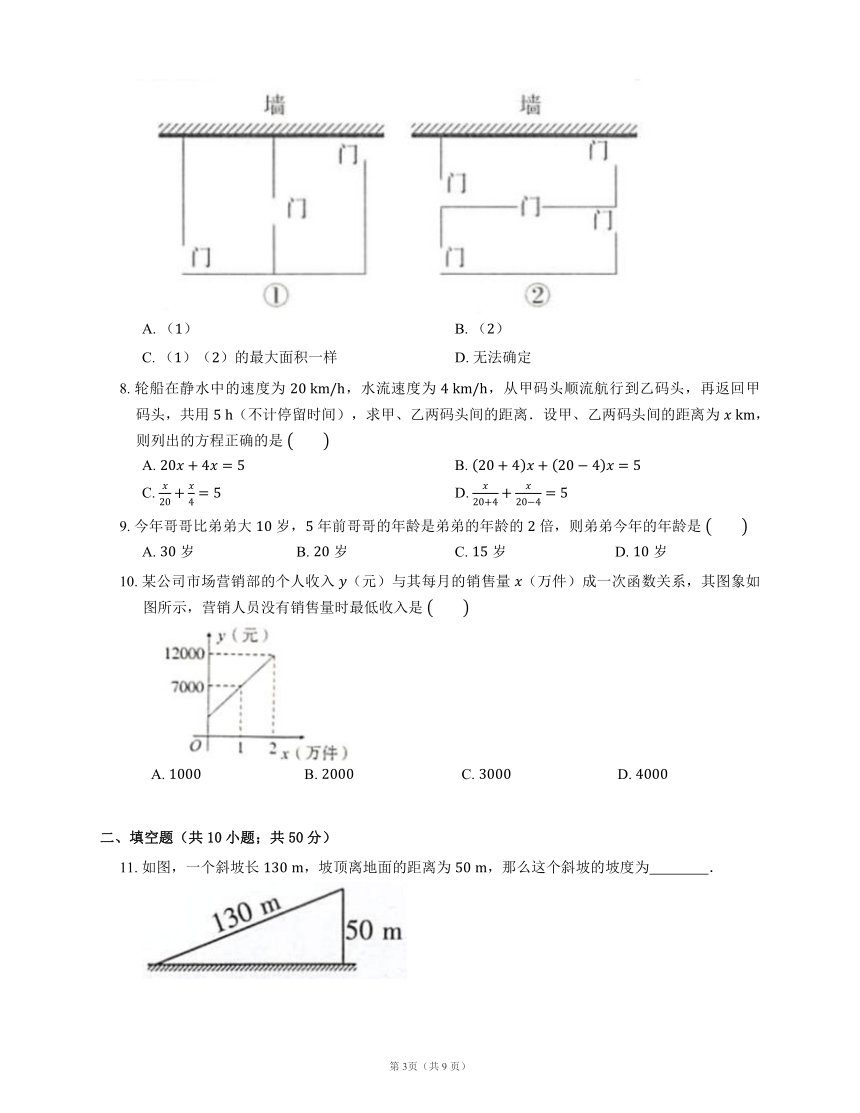
7. 某牧民计划用 长的篱笆围成矩形羊圈,一面靠墙(墙足够长),现有两种方案供选择:方案()(如图①):中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留 宽的门;方案()(如图②):中间用一道平行于墙的篱笆隔开,并在如图所示的五处各留 宽的门,则能建成的羊圈中面积最大的方案为
A. () B. ()
C. ()()的最大面积一样 D. 无法确定
8. 轮船在静水中的速度为 ,水流速度为 ,从甲码头顺流航行到乙码头,再返回甲码头,共用 (不计停留时间),求甲、乙两码头间的距离.设甲、乙两码头间的距离为 ,则列出的方程正确的是
A. B.
C. D.
9. 今年哥哥比弟弟大 岁, 年前哥哥的年龄是弟弟的年龄的 倍,则弟弟今年的年龄是
A. 岁 B. 岁 C. 岁 D. 岁
10. 某公司市场营销部的个人收入 (元)与其每月的销售量 (万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 如图,一个斜坡长 ,坡顶离地面的距离为 ,那么这个斜坡的坡度为 .
12. 一批服装,按期望获得 的利润来定价.结果只销掉 .为尽早销掉剩下的服装,商店决定按定价打折扣销售.这样所获得的全部利润,是原来期望利润的 ,那么这件服装打了 折.
13. 某车间第一个月生产了 个零件,第二个月比第一个月增产 ,那么这两个月该车间共生产零件 个.
14. 某小组有若干人,新年大家互相发一条微信祝福,已知全组共发微信 条,则这个小组的人数为 人.
15. 某学校举办一次数学知识竞赛活动,竞赛题共有 道题,规定做对一道题得 分,不做或做错一道题扣 分.李伟最后的竞赛成绩是 分,那么李伟一共做对了 道题.
16. 一个两位数,个位数字比十位数字的 倍多 ,如果个位与十位的数字交换位置,得到一个新的两位数,新的两位数比原来两位数的 倍少 ,则原两位数为 .
17. 把一个长、宽、高分别为 ,, 的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积 与高 之间的函数解析式为 .
18. 一根绳子,剪去 米后,剩下的部分比全长的 少 米,这根绳子全长 米.
19. 已知:派派妈妈和派派今年共 岁,再过 年,派派妈妈的年龄比派派年龄的 倍还大 岁,当派派的妈妈 岁时,则派派的年龄为 岁.
20. 年 月 日 时 分,被称为“千里淮河第一闸”的王家坝闸时隔 年再开闸,向蒙洼蓄洪区分洪.如图,位于上游支流有一座抛物线型拱桥,当达到警戒水位时,水面 的宽是 ,拱顶距离水面 米,正常水位时,水面 的宽为 ,如果从开始泄洪后,水位以 的速度匀速下降,那么开始泄洪后,再过 水位达到正常水位.
三、解答题(共6小题;共50分)
21. 某车间每天能生产甲种零件 个,或乙种零件 个,甲、乙两种零件分别取 个、 个才能配成一套.若在 天内生产的产品刚好配套,则怎样安排生产甲、乙两种零件的天数
22. 有若干张小长方形的纸片,已知每张纸片的长和宽的和等于 .茗茗用 张这样的纸片拼出了如图 所示的大长方形,墨墨用 张这样的纸片拼出了如图 所示的大正方形.求:
(1)茗茗所拼大长方形的周长;
(2)墨墨所拼大正方形中间小正方形的面积.
23. 放学后,小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本,这种笔芯每盒 支,如果整盒买比单支买每支可优惠 元.小贤要买 支笔芯, 本笔记本需花费 元;小艺要买 支笔芯, 本笔记本需花费 元.
(1)求笔记本的单价和单独购买一支笔芯的价格;
(2)小贤和小艺都还想再买 件单价为 元的小工艺品,但如果他们各自为要买的文具付款后,只有小贤还剩 元钱.他们要怎样做才能既买到各自的文具,又都买到小工艺品 请通过运算说明.
24. 为了帮助贫困家庭脱贫,精准扶贫小组帮助一农户建立如图所示的长方形养鸡场 ,养鸡场的面积为 (中间隔开),养鸡场的一边靠着一面长为 的墙,另几条边用总长为 的竹篱笆围成,养鸡场的前面开有两个宽为 的门,求这个养鸡场的长与宽.
25. 某校欲将上海市教委调拨的几台电脑配给英语教师,若三人合用一台,则缺一台;若四人合用一台,则有一台电脑只有三个人合用.问:该校有英语教师多少人 这批电脑共有几台
26. “ 天无理由退货”是营造我省“诚信旅游”良好环境,进一步提升旅游形象的创新举措.机场、车站、出租车、景区、手机短信 ,“ 天无理由退货”的提示随处可见,它已成为一张云南旅行的“安心卡”,极大地提高了旅游服务的品质.刚刚过去的“五 一”假期,旅游线路、住宿、餐饮、生活服务、购物等旅游消费的供给更加多元,同步的是云南旅游市场强劲复苏.某旅行社今年 月 日租用A,B两种客房一天,供当天使用.下面是有关信息:
请根据上述信息,分别求今年 月 日该旅行社租用的A,B两种客房每间客房的租金.
答案
第一部分
1. A
2. C 【解析】设这一年期的利率为 ,由题意得 ,
解得 ,
即这一年期的利率为 .
3. C
4. C 【解析】设这个队胜了 场,则平了 场,根据题意,得 ,解得 .
5. C
【解析】①小明家距学校 千米,正确;
②小明上学所用的时间为 分钟,正确;
③小明上坡的速度是 千米/分钟,错误;
④小明放学回家所用时间为 分钟,正确;
故选:C.
6. A 【解析】设中间一个数为 ,则它左边的数是 ,右边的数是 ,
则 ,
因为 ,,,,
所以它们的和不可能是 .
故选A.
7. A 【解析】对于方案(),设矩形垂直于墙的边长为 ,面积为 ,则平行于墙的边长为 ,
所以 ,即当 时, 最大,最大值为 ;
对于方案(),设矩形垂直于墙的边长为 ,面积为 ,则平行于墙的边长为 ,
所以 ,即当 时, 最大,最大值为 .
因为 ,
所以面积最大的方案是().
8. D 【解析】根据题意,可列方程为 .
9. C 【解析】设弟弟今年 岁,
则哥哥今年为 岁,
年前弟弟为 ,
哥哥为 岁,
,
,
,
,
弟弟今年 岁.
10. B
第二部分
11.
12. 九
13.
14.
15.
16.
【解析】设原两位数的十位数字为 ,则个位上的数字为 .
根据题意,得 ,解这个方程,得 .
所以 .
故原来的两位数为 .
17.
【解析】由题意,得 ,则 .
18.
19.
【解析】设今年派派的年龄为 岁,则妈妈的年龄为 岁.
根据题意,得 ,
解得 ,
所以 ,
则妈妈与派派的年龄差为 (岁),
所以 (岁).
20.
【解析】以拱顶为原点,水平方向为 轴建立平面直角坐标系(图略),
设抛物线的解析式为 ,
因为抛物线关于 轴对称,,
所以点 的横坐标为 ,原点距离 米,
所以点 的坐标为 ,
把 代入 ,得 ,
所以抛物线的解析式为 ,
因为 ,
所以 点的横坐标为 ,
当 时,,
,
则 .
第三部分
21. 设安排生产甲种零件 天,则安排生产乙种零件 天.
根据题意,得
解得
所以 .
答:安排生产甲种零件 天,乙种零件 天.
22. (1) 设小长方形的长为 ,则宽为 .
由图 可知, 个小长方形的宽等于 个小长方形的长,列出方程
解得
所以 .
大长方形的长为 ,宽为 ,周长为 .
答:茗茗所拼大长方形的周长为 .
(2) 由图 可知,墨墨所拼的小正方形的边长为 ,
小正方形的面积为 .
答:墨墨所拼大正方形中间小正方形的面积为 .
23. (1) 设笔记本的单价为 元,单独购买一支笔芯的价格为 元,
依题意,得
解得
答:笔记本的单价为 元,单独购买一支笔芯的价格为 元.
(2) 解法一:合买笔芯,合算,
小贤和小艺带的总钱数为 (元).
两人合在一起购买所需费用为 (元).
(元),(元),,
他们合在一起购买笔芯(合算),既买到各自的文具,又都买到小工艺品.
【解析】解法二:合买笔芯,单算,
小贤购买完文具后剩余钱数为 (元),;
小艺购买完文具后剩余钱数为 (元),.
他们合在一起购买笔芯(单算),既买到各自的文具,又都买到小工艺品.
24. 设养鸡场靠墙的一边 的长为 ,则另一边 的长为 .
由题意,得
解得
.
答:这个养鸡场的长为 ,宽为 .
25. 该校英语教师有 人,这批电脑共有 台.
26. 设每间B客房租金为 元,则每间A客房租金为 元,
根据题意可得:
解得:
经检验: 是原分式方程的解,且符合实际,
元,
每间A客房租金为 元,每间B客房租金为 元.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 如图所示,小红将一个正方形纸片剪去一个宽为 的长条后,再从剩下的长方形纸片上剪去一个宽为 的长条,且剪下的两个长条的面积相等,问这个正方形的边长应为多少,设正方形的边长为 ,则可列方程为
A. B.
C. D.
2. 杰杰去银行存入本金 元,作为一年期的定期储蓄,到期后杰杰共取了 元,则这一年期的利率为
A. B. C. D.
3. 某通信公司自 年 月 日起实行新的 飞享套餐,部分套餐资费标准如下表:
小明每月大约使用国内数据流量 ,国内主叫 分钟,若想使每月付费最少,则他应预定的套餐是
A. 套餐 B. 套餐 C. 套餐 D. 套餐
4. 足球比赛的规则为胜一场得 分,平一场得 分,负一场得 分,一个足球队踢了 场比赛,负了 场,共得 分,那么这个队胜了的场数是
A. B. C. D.
5. 小明早上从家骑自行车去上学,先走平路到达点 ,再走上坡路到达点 ,最后走下坡路到达学校,小明骑自行车所走的路程 (单位:千米)与他所用的时间 (单位:分钟)的关系如图所示,放学后,小明沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,下列说法:
①小明家距学校 千米;
②小明上学所用的时间为 分钟;
③小明上坡的速度是 千米/分钟;
④小明放学回家所用时间为 分钟.
其中正确的个数是
A. 个 B. 个 C. 个 D. 个
6. 如图是某月的月历,横着取连续的三个数字,它们的和不可能是
A. B. C. D.
7. 某牧民计划用 长的篱笆围成矩形羊圈,一面靠墙(墙足够长),现有两种方案供选择:方案()(如图①):中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留 宽的门;方案()(如图②):中间用一道平行于墙的篱笆隔开,并在如图所示的五处各留 宽的门,则能建成的羊圈中面积最大的方案为
A. () B. ()
C. ()()的最大面积一样 D. 无法确定
8. 轮船在静水中的速度为 ,水流速度为 ,从甲码头顺流航行到乙码头,再返回甲码头,共用 (不计停留时间),求甲、乙两码头间的距离.设甲、乙两码头间的距离为 ,则列出的方程正确的是
A. B.
C. D.
9. 今年哥哥比弟弟大 岁, 年前哥哥的年龄是弟弟的年龄的 倍,则弟弟今年的年龄是
A. 岁 B. 岁 C. 岁 D. 岁
10. 某公司市场营销部的个人收入 (元)与其每月的销售量 (万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 如图,一个斜坡长 ,坡顶离地面的距离为 ,那么这个斜坡的坡度为 .
12. 一批服装,按期望获得 的利润来定价.结果只销掉 .为尽早销掉剩下的服装,商店决定按定价打折扣销售.这样所获得的全部利润,是原来期望利润的 ,那么这件服装打了 折.
13. 某车间第一个月生产了 个零件,第二个月比第一个月增产 ,那么这两个月该车间共生产零件 个.
14. 某小组有若干人,新年大家互相发一条微信祝福,已知全组共发微信 条,则这个小组的人数为 人.
15. 某学校举办一次数学知识竞赛活动,竞赛题共有 道题,规定做对一道题得 分,不做或做错一道题扣 分.李伟最后的竞赛成绩是 分,那么李伟一共做对了 道题.
16. 一个两位数,个位数字比十位数字的 倍多 ,如果个位与十位的数字交换位置,得到一个新的两位数,新的两位数比原来两位数的 倍少 ,则原两位数为 .
17. 把一个长、宽、高分别为 ,, 的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积 与高 之间的函数解析式为 .
18. 一根绳子,剪去 米后,剩下的部分比全长的 少 米,这根绳子全长 米.
19. 已知:派派妈妈和派派今年共 岁,再过 年,派派妈妈的年龄比派派年龄的 倍还大 岁,当派派的妈妈 岁时,则派派的年龄为 岁.
20. 年 月 日 时 分,被称为“千里淮河第一闸”的王家坝闸时隔 年再开闸,向蒙洼蓄洪区分洪.如图,位于上游支流有一座抛物线型拱桥,当达到警戒水位时,水面 的宽是 ,拱顶距离水面 米,正常水位时,水面 的宽为 ,如果从开始泄洪后,水位以 的速度匀速下降,那么开始泄洪后,再过 水位达到正常水位.
三、解答题(共6小题;共50分)
21. 某车间每天能生产甲种零件 个,或乙种零件 个,甲、乙两种零件分别取 个、 个才能配成一套.若在 天内生产的产品刚好配套,则怎样安排生产甲、乙两种零件的天数
22. 有若干张小长方形的纸片,已知每张纸片的长和宽的和等于 .茗茗用 张这样的纸片拼出了如图 所示的大长方形,墨墨用 张这样的纸片拼出了如图 所示的大正方形.求:
(1)茗茗所拼大长方形的周长;
(2)墨墨所拼大正方形中间小正方形的面积.
23. 放学后,小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本,这种笔芯每盒 支,如果整盒买比单支买每支可优惠 元.小贤要买 支笔芯, 本笔记本需花费 元;小艺要买 支笔芯, 本笔记本需花费 元.
(1)求笔记本的单价和单独购买一支笔芯的价格;
(2)小贤和小艺都还想再买 件单价为 元的小工艺品,但如果他们各自为要买的文具付款后,只有小贤还剩 元钱.他们要怎样做才能既买到各自的文具,又都买到小工艺品 请通过运算说明.
24. 为了帮助贫困家庭脱贫,精准扶贫小组帮助一农户建立如图所示的长方形养鸡场 ,养鸡场的面积为 (中间隔开),养鸡场的一边靠着一面长为 的墙,另几条边用总长为 的竹篱笆围成,养鸡场的前面开有两个宽为 的门,求这个养鸡场的长与宽.
25. 某校欲将上海市教委调拨的几台电脑配给英语教师,若三人合用一台,则缺一台;若四人合用一台,则有一台电脑只有三个人合用.问:该校有英语教师多少人 这批电脑共有几台
26. “ 天无理由退货”是营造我省“诚信旅游”良好环境,进一步提升旅游形象的创新举措.机场、车站、出租车、景区、手机短信 ,“ 天无理由退货”的提示随处可见,它已成为一张云南旅行的“安心卡”,极大地提高了旅游服务的品质.刚刚过去的“五 一”假期,旅游线路、住宿、餐饮、生活服务、购物等旅游消费的供给更加多元,同步的是云南旅游市场强劲复苏.某旅行社今年 月 日租用A,B两种客房一天,供当天使用.下面是有关信息:
请根据上述信息,分别求今年 月 日该旅行社租用的A,B两种客房每间客房的租金.
答案
第一部分
1. A
2. C 【解析】设这一年期的利率为 ,由题意得 ,
解得 ,
即这一年期的利率为 .
3. C
4. C 【解析】设这个队胜了 场,则平了 场,根据题意,得 ,解得 .
5. C
【解析】①小明家距学校 千米,正确;
②小明上学所用的时间为 分钟,正确;
③小明上坡的速度是 千米/分钟,错误;
④小明放学回家所用时间为 分钟,正确;
故选:C.
6. A 【解析】设中间一个数为 ,则它左边的数是 ,右边的数是 ,
则 ,
因为 ,,,,
所以它们的和不可能是 .
故选A.
7. A 【解析】对于方案(),设矩形垂直于墙的边长为 ,面积为 ,则平行于墙的边长为 ,
所以 ,即当 时, 最大,最大值为 ;
对于方案(),设矩形垂直于墙的边长为 ,面积为 ,则平行于墙的边长为 ,
所以 ,即当 时, 最大,最大值为 .
因为 ,
所以面积最大的方案是().
8. D 【解析】根据题意,可列方程为 .
9. C 【解析】设弟弟今年 岁,
则哥哥今年为 岁,
年前弟弟为 ,
哥哥为 岁,
,
,
,
,
弟弟今年 岁.
10. B
第二部分
11.
12. 九
13.
14.
15.
16.
【解析】设原两位数的十位数字为 ,则个位上的数字为 .
根据题意,得 ,解这个方程,得 .
所以 .
故原来的两位数为 .
17.
【解析】由题意,得 ,则 .
18.
19.
【解析】设今年派派的年龄为 岁,则妈妈的年龄为 岁.
根据题意,得 ,
解得 ,
所以 ,
则妈妈与派派的年龄差为 (岁),
所以 (岁).
20.
【解析】以拱顶为原点,水平方向为 轴建立平面直角坐标系(图略),
设抛物线的解析式为 ,
因为抛物线关于 轴对称,,
所以点 的横坐标为 ,原点距离 米,
所以点 的坐标为 ,
把 代入 ,得 ,
所以抛物线的解析式为 ,
因为 ,
所以 点的横坐标为 ,
当 时,,
,
则 .
第三部分
21. 设安排生产甲种零件 天,则安排生产乙种零件 天.
根据题意,得
解得
所以 .
答:安排生产甲种零件 天,乙种零件 天.
22. (1) 设小长方形的长为 ,则宽为 .
由图 可知, 个小长方形的宽等于 个小长方形的长,列出方程
解得
所以 .
大长方形的长为 ,宽为 ,周长为 .
答:茗茗所拼大长方形的周长为 .
(2) 由图 可知,墨墨所拼的小正方形的边长为 ,
小正方形的面积为 .
答:墨墨所拼大正方形中间小正方形的面积为 .
23. (1) 设笔记本的单价为 元,单独购买一支笔芯的价格为 元,
依题意,得
解得
答:笔记本的单价为 元,单独购买一支笔芯的价格为 元.
(2) 解法一:合买笔芯,合算,
小贤和小艺带的总钱数为 (元).
两人合在一起购买所需费用为 (元).
(元),(元),,
他们合在一起购买笔芯(合算),既买到各自的文具,又都买到小工艺品.
【解析】解法二:合买笔芯,单算,
小贤购买完文具后剩余钱数为 (元),;
小艺购买完文具后剩余钱数为 (元),.
他们合在一起购买笔芯(单算),既买到各自的文具,又都买到小工艺品.
24. 设养鸡场靠墙的一边 的长为 ,则另一边 的长为 .
由题意,得
解得
.
答:这个养鸡场的长为 ,宽为 .
25. 该校英语教师有 人,这批电脑共有 台.
26. 设每间B客房租金为 元,则每间A客房租金为 元,
根据题意可得:
解得:
经检验: 是原分式方程的解,且符合实际,
元,
每间A客房租金为 元,每间B客房租金为 元.
第1页(共1 页)
