16.2.二次根式的运算(第1课时) 课件(共27张PPT)
文档属性
| 名称 | 16.2.二次根式的运算(第1课时) 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 17:37:35 | ||
图片预览








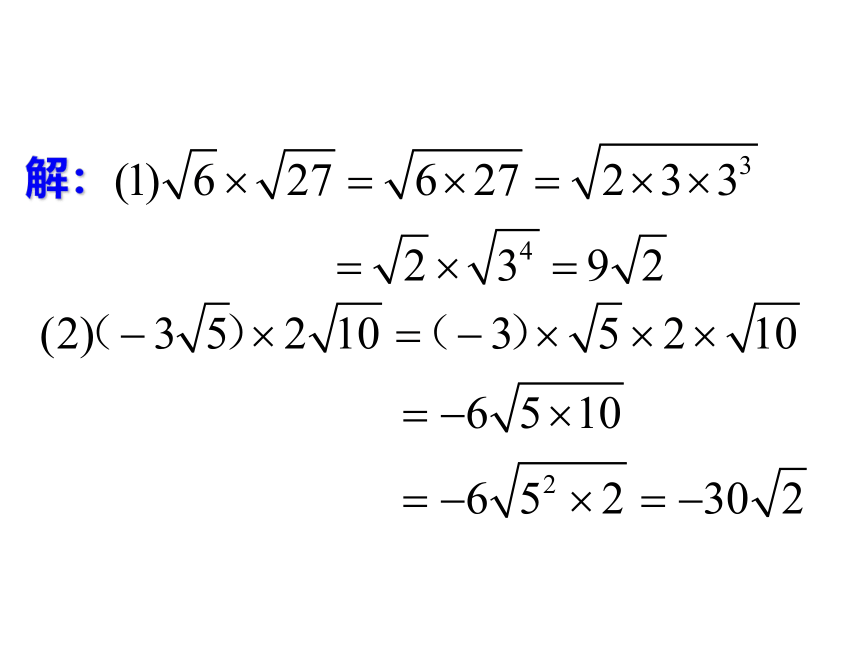
文档简介
(共27张PPT)
二次根式
被开方数a≥0;
根指数为2.
复习回顾
当x为怎样的实数时,下列各式有意义?
x≥3
x≤6
∴3≤x≤6
x≥1
x≤1
∴x=1
x为任何实数.
x为任何实数.
复习回顾
这个结果能否化简?如何化简?
你发现了什么?用你发现的规律填空:
讨论
10
10
2、计算:
=
=
探究
不成立!
一般情况下,a≥0,b≥0时, 与
有什么关系?
(a≥0,b≥0)
性质3 一般地,如果a≥0,b≥0时,
例题讲解
例1 计算:
解:
根号外的系数与系数相乘,积为结果的系数.
二次根式的乘法:根式和根式按公式相乘.
分析
练习
计算:
解:
解:
计算:
讨论
有什么发现?
=
=
根据你发现的规律填空:
(a≥0,b>0 )
性质4 如果a≥0,b>0,则有
例题讲解
例2 计算:
解:
最简二次根式
1、被开方数的因数是整数,因式是整式;
2、被开方数中不含能开得尽方的因数或因式。
我们把满足上述两个条件的二次根式叫做最简二次根式。
二次根式的运算中,最后的结果中的二次根式一般要写成最简二次根式的形式.
下列根式中,哪些是最简二次根式?
探究
√
×
×
×
×
×
√
√
√
例
3
化
简
:
例题讲解
例题讲解
解:
计算:
解:(1)
解法一:
解法二:
在二次根式的运算中,一般要求最后结果的分母中不含根式.
计算:
二次根式的混合运算,从左向右依次计算.
梳理
(a≥0,b≥0)
(a≥0,b>0)
最简二次根式
巩固练习
1、化简:
2、计算:
学而不思则罔,思而不学则殆。
——孔子
二次根式
被开方数a≥0;
根指数为2.
复习回顾
当x为怎样的实数时,下列各式有意义?
x≥3
x≤6
∴3≤x≤6
x≥1
x≤1
∴x=1
x为任何实数.
x为任何实数.
复习回顾
这个结果能否化简?如何化简?
你发现了什么?用你发现的规律填空:
讨论
10
10
2、计算:
=
=
探究
不成立!
一般情况下,a≥0,b≥0时, 与
有什么关系?
(a≥0,b≥0)
性质3 一般地,如果a≥0,b≥0时,
例题讲解
例1 计算:
解:
根号外的系数与系数相乘,积为结果的系数.
二次根式的乘法:根式和根式按公式相乘.
分析
练习
计算:
解:
解:
计算:
讨论
有什么发现?
=
=
根据你发现的规律填空:
(a≥0,b>0 )
性质4 如果a≥0,b>0,则有
例题讲解
例2 计算:
解:
最简二次根式
1、被开方数的因数是整数,因式是整式;
2、被开方数中不含能开得尽方的因数或因式。
我们把满足上述两个条件的二次根式叫做最简二次根式。
二次根式的运算中,最后的结果中的二次根式一般要写成最简二次根式的形式.
下列根式中,哪些是最简二次根式?
探究
√
×
×
×
×
×
√
√
√
例
3
化
简
:
例题讲解
例题讲解
解:
计算:
解:(1)
解法一:
解法二:
在二次根式的运算中,一般要求最后结果的分母中不含根式.
计算:
二次根式的混合运算,从左向右依次计算.
梳理
(a≥0,b≥0)
(a≥0,b>0)
最简二次根式
巩固练习
1、化简:
2、计算:
学而不思则罔,思而不学则殆。
——孔子
