23.1.3一般锐角的三角函数值(第2课时) 课件(共12张PPT)
文档属性
| 名称 | 23.1.3一般锐角的三角函数值(第2课时) 课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 16:29:03 | ||
图片预览





文档简介
(共12张PPT)
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tan A
cos A
∠A的邻边
∠A的对边
斜边
sin A
斜边
斜边
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:
sin A=cos B,tan A·tan B=1.
同角之间的三角函数关系:
sin2A+cos2A=1.
tan A=
a
b
特殊角30°,45°,60°角的三角函数值.
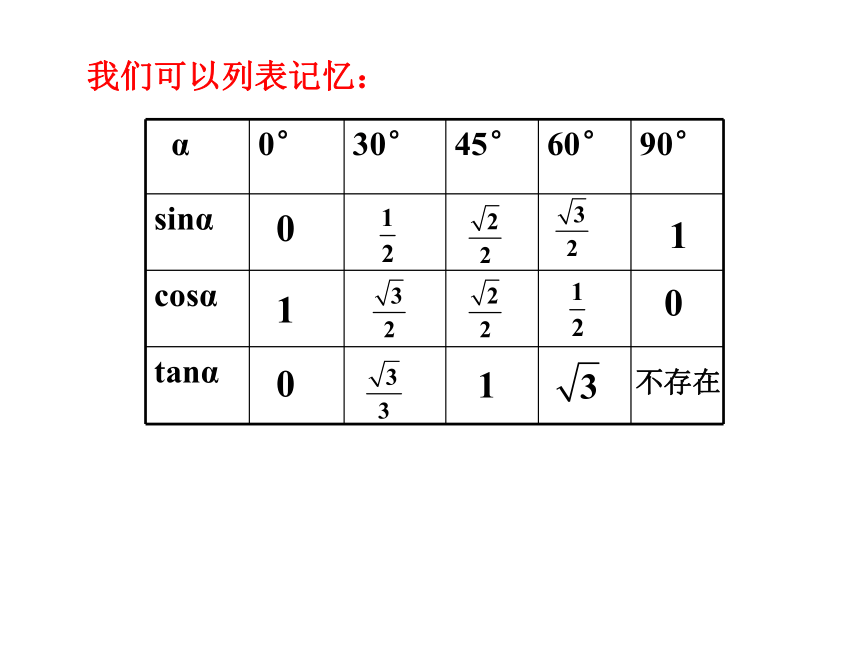
我们可以列表记忆:
α 0° 30° 45° 60° 90°
sinα
cosα
tanα
0
1
1
0
0
不存在
☆ 应用练习
1.已知角,求值
确定值的范围
2.已知值,求角
3. 确定值的范围
1. 当 锐角A>45°时,sin A的值( )
(A)小于 (B)大于
(C) 小于 (D)大于
B
(A)小于 (B)大于
(C) 小于 (D)大于
2. 当锐角A>30°时,cos A的值( )
C
上一页
下一页
☆ 应用练习
1.已知角,求值
确定角的范围
2.已知值,求角
3. 确定值的范围
(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°
3. 当∠A为锐角,且tan A的值大于 时,∠A( )
B
4. 确定角的范围
4. 当∠A为锐角,且tan A的值小于 时,∠A( )
(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°
C
☆ 应用练习
1.已知角,求值
2.已知值,求角
3. 确定值的范围
5.当∠A为锐角,且cos A=
那么( )
4. 确定角的范围
(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 °
确定角的范围
6. 当∠A为锐角,且sin A=
那么( )
(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 °
D
A
按键的顺序 显示结果
SHIFT
2
0
9
17.30150783
4
sin
·
7
=
已知三角函数值求角度,要用到sin,cos,tan的第二功能健“sin-1 Cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:
如果再按“度分秒健”就换算成度分秒,
°′″
即∠α=17°18′5.43″
按键的顺序 显示结果
17°18′5.43″
2ndf
2
0
9
4
sin
·
7
已知三角函数值求角度,要用到sin,cos,tan的第二功能健“sin-1, cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:
即∠α =17°18′5.43″
2ndf
DMS
例如,根据下面的条件,求锐角β的大小(精确到1″
(1)sinβ=0.4511;(2)cosβ=0.7857;
(3) tanβ=1.4036
按键盘顺序如下:
按键的顺序 显示结果
26°48′51″
0
.
sin
1
1
5
=
4
DMS
SHIFT
°′″
2ndf
sin
0
.
4
5
1
1
2ndf
26°48′51″
即∠β=26°48′51″
例 如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到1° ).
∴∠ACD≈27.5° .
∴∠ACB=2∠ACD≈2×27.5°=55°.
∴V型角的大小约55°.
谈谈今天的收获
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tan A
cos A
∠A的邻边
∠A的对边
斜边
sin A
斜边
斜边
b
A
B
C
a
┌
c
互余两角之间的三角函数关系:
sin A=cos B,tan A·tan B=1.
同角之间的三角函数关系:
sin2A+cos2A=1.
tan A=
a
b
特殊角30°,45°,60°角的三角函数值.
我们可以列表记忆:
α 0° 30° 45° 60° 90°
sinα
cosα
tanα
0
1
1
0
0
不存在
☆ 应用练习
1.已知角,求值
确定值的范围
2.已知值,求角
3. 确定值的范围
1. 当 锐角A>45°时,sin A的值( )
(A)小于 (B)大于
(C) 小于 (D)大于
B
(A)小于 (B)大于
(C) 小于 (D)大于
2. 当锐角A>30°时,cos A的值( )
C
上一页
下一页
☆ 应用练习
1.已知角,求值
确定角的范围
2.已知值,求角
3. 确定值的范围
(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°
3. 当∠A为锐角,且tan A的值大于 时,∠A( )
B
4. 确定角的范围
4. 当∠A为锐角,且tan A的值小于 时,∠A( )
(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°
C
☆ 应用练习
1.已知角,求值
2.已知值,求角
3. 确定值的范围
5.当∠A为锐角,且cos A=
那么( )
4. 确定角的范围
(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 °
确定角的范围
6. 当∠A为锐角,且sin A=
那么( )
(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 °
D
A
按键的顺序 显示结果
SHIFT
2
0
9
17.30150783
4
sin
·
7
=
已知三角函数值求角度,要用到sin,cos,tan的第二功能健“sin-1 Cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:
如果再按“度分秒健”就换算成度分秒,
°′″
即∠α=17°18′5.43″
按键的顺序 显示结果
17°18′5.43″
2ndf
2
0
9
4
sin
·
7
已知三角函数值求角度,要用到sin,cos,tan的第二功能健“sin-1, cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:
即∠α =17°18′5.43″
2ndf
DMS
例如,根据下面的条件,求锐角β的大小(精确到1″
(1)sinβ=0.4511;(2)cosβ=0.7857;
(3) tanβ=1.4036
按键盘顺序如下:
按键的顺序 显示结果
26°48′51″
0
.
sin
1
1
5
=
4
DMS
SHIFT
°′″
2ndf
sin
0
.
4
5
1
1
2ndf
26°48′51″
即∠β=26°48′51″
例 如图,工件上有一V型槽,测得它的上口宽20mm,深19.2mm.求V型角(∠ACB)的大小(结果精确到1° ).
∴∠ACD≈27.5° .
∴∠ACB=2∠ACD≈2×27.5°=55°.
∴V型角的大小约55°.
谈谈今天的收获
