23.2解直角三角形及其应用(第1课时) 课件(共14张PPT)
文档属性
| 名称 | 23.2解直角三角形及其应用(第1课时) 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 16:31:12 | ||
图片预览



文档简介
(共14张PPT)
第1课时
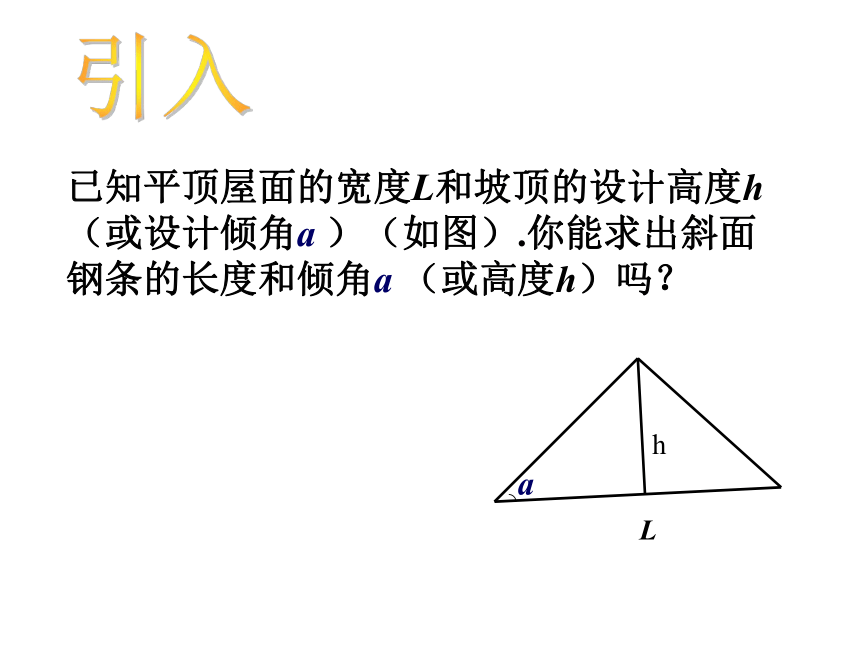
已知平顶屋面的宽度L和坡顶的设计高度h(或设计倾角a )(如图).你能求出斜面钢条的长度和倾角a (或高度h)吗?
h
L
a
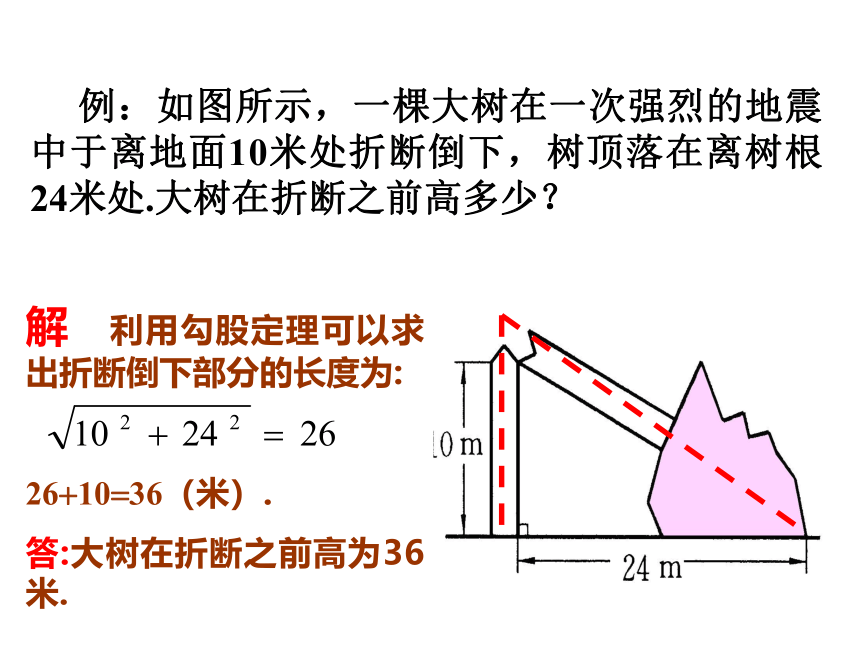
例:如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
在例题中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样:
********************************
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
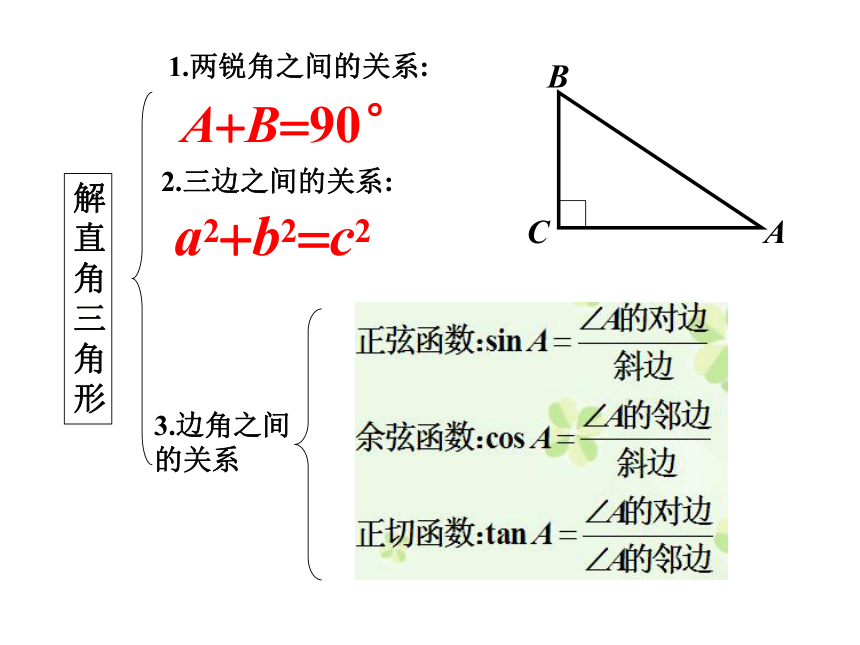
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
A+B=90°
a2+b2=c2
C
A
B
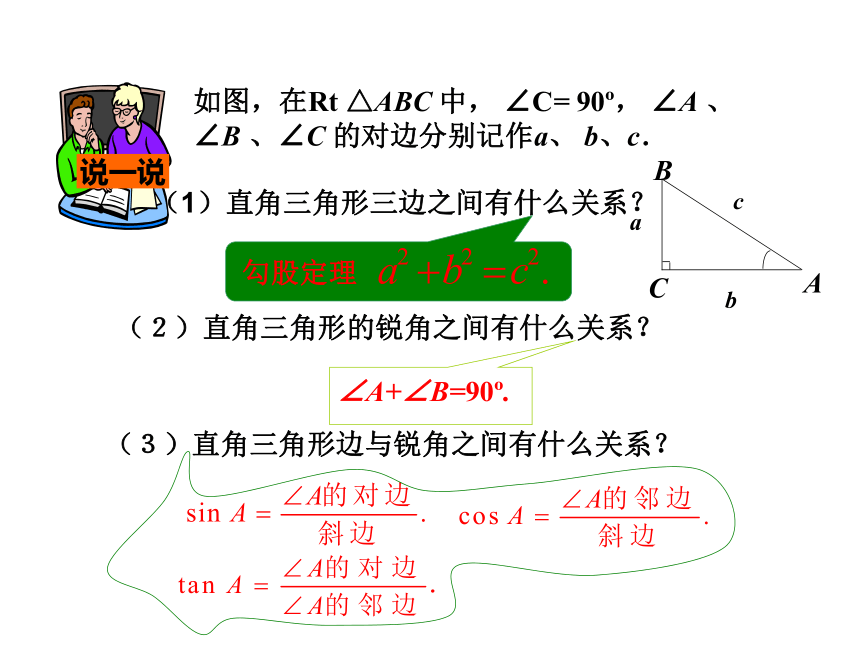
说一说
(2)直角三角形的锐角之间有什么关系?
(1)直角三角形三边之间有什么关系?
(3)直角三角形边与锐角之间有什么关系?
如图,在Rt △ABC 中, ∠C= 90 , ∠A 、∠B 、∠C 的对边分别记作a、 b、c.
B
C
A
b
a
c
勾股定理
∠A+∠B=90 .
做一做
根据下列每一组条件,能画出多少个直角三角形(全等的直角三角形算一个)?
(1)一个锐角为40 ;
(2)一个锐角为40 ,它的邻边长为3cm;
(3)一个锐角为40 ,它的对边长为3cm;
(4)一个锐角为40 ,它的斜边长为3cm;
(5)斜边长为4cm,一条直角边长为3cm.
(无数个)
(一个)
(一个)
(一个)
(一个)
从这些问题的结论,你猜想有什么规律?
总结
在直角三角形中,除直角外的5个元素(3条边和2个锐角),只要知道其中的2个元素(至少有一个是边),就可求出其余的3个未知元素,这叫作
解直角三角形.
考 虑
如果知道的2个元素都是角,能求出直角三角形的边吗?
1.如图,在Rt △ABC 中,∠C= 90 , ∠A =26 8′,b=4,求∠B 、a、 c (精确到0.01).
又∵a 是∠A 的对边,于是
B
C
A
b
a
c
例 题
解
2.如图,在Rt △ABC 中, ∠C= 90 ,a=15.6cm,b=8.50cm, 求c 、∠A、 ∠B (长度精确到0.01cm,角度精确到1').
由于
从而
例 题
B
C
A
b
a
c
解
基 础
练 习
2.如图,在Rt △ABC 中, ∠C= 90 ,∠A=38 12′, c=15.68cm,求∠B, a, b(精确到0.01cm).
巩 固
练 习
解
B
C
A
b
a
c
在直角三角形ABC中,∠C=90 ,
只要知道除直角外的任意两个元素(至少有一个是边),就可以求出其余的元素.
小结
三条边满足
两个锐角满足∠A+∠B=90 ,
第1课时
已知平顶屋面的宽度L和坡顶的设计高度h(或设计倾角a )(如图).你能求出斜面钢条的长度和倾角a (或高度h)吗?
h
L
a
例:如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
在例题中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样:
********************************
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
A+B=90°
a2+b2=c2
C
A
B
说一说
(2)直角三角形的锐角之间有什么关系?
(1)直角三角形三边之间有什么关系?
(3)直角三角形边与锐角之间有什么关系?
如图,在Rt △ABC 中, ∠C= 90 , ∠A 、∠B 、∠C 的对边分别记作a、 b、c.
B
C
A
b
a
c
勾股定理
∠A+∠B=90 .
做一做
根据下列每一组条件,能画出多少个直角三角形(全等的直角三角形算一个)?
(1)一个锐角为40 ;
(2)一个锐角为40 ,它的邻边长为3cm;
(3)一个锐角为40 ,它的对边长为3cm;
(4)一个锐角为40 ,它的斜边长为3cm;
(5)斜边长为4cm,一条直角边长为3cm.
(无数个)
(一个)
(一个)
(一个)
(一个)
从这些问题的结论,你猜想有什么规律?
总结
在直角三角形中,除直角外的5个元素(3条边和2个锐角),只要知道其中的2个元素(至少有一个是边),就可求出其余的3个未知元素,这叫作
解直角三角形.
考 虑
如果知道的2个元素都是角,能求出直角三角形的边吗?
1.如图,在Rt △ABC 中,∠C= 90 , ∠A =26 8′,b=4,求∠B 、a、 c (精确到0.01).
又∵a 是∠A 的对边,于是
B
C
A
b
a
c
例 题
解
2.如图,在Rt △ABC 中, ∠C= 90 ,a=15.6cm,b=8.50cm, 求c 、∠A、 ∠B (长度精确到0.01cm,角度精确到1').
由于
从而
例 题
B
C
A
b
a
c
解
基 础
练 习
2.如图,在Rt △ABC 中, ∠C= 90 ,∠A=38 12′, c=15.68cm,求∠B, a, b(精确到0.01cm).
巩 固
练 习
解
B
C
A
b
a
c
在直角三角形ABC中,∠C=90 ,
只要知道除直角外的任意两个元素(至少有一个是边),就可以求出其余的元素.
小结
三条边满足
两个锐角满足∠A+∠B=90 ,
