2.2 整式加减 第1课时 课件(共20张PPT)
文档属性
| 名称 | 2.2 整式加减 第1课时 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 876.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 09:24:59 | ||
图片预览








文档简介
(共20张PPT)
沪科版七年级上册
如图,在长为a,宽为b的长方形空地的中
间,有一块长为 ,宽为 的长方形
花圃,而长方形空地的其余地方种了草.
试问:草地的面积是多少?
a
b
草地的面积为
利用乘法分配律,得
因此草地的面积是
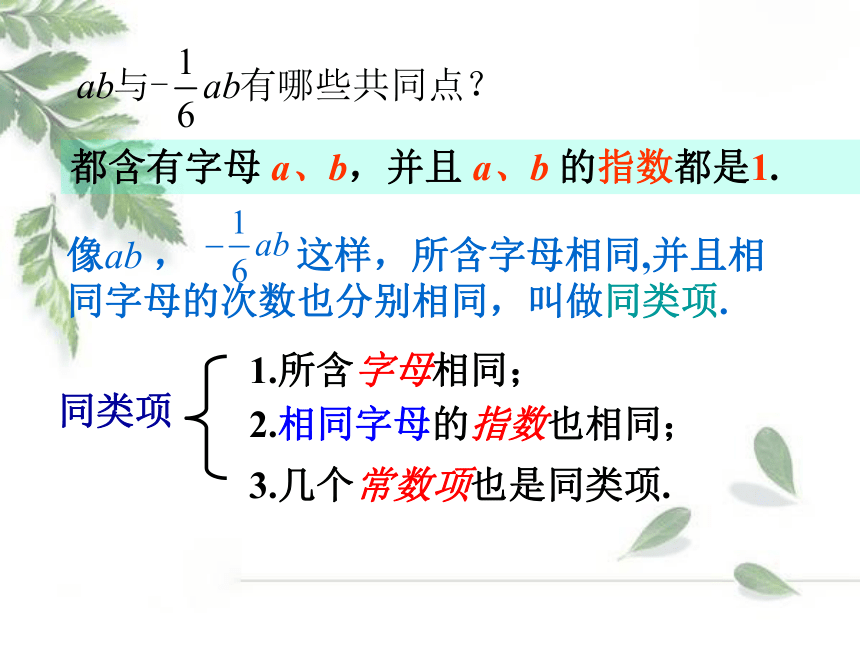
都含有字母 a、b,并且 a、b 的指数都是1.
像ab , 这样,所含字母相同,并且相同字母的次数也分别相同,叫做同类项.
1.所含字母相同;
2.相同字母的指数也相同;
3.几个常数项也是同类项.
同类项
同类项要素:
(1)各项中所含的字母相同.
(2)相同字母的指数相同.
(1)3ab与-2abc;
(2)2a2b3与-3a3b2;
(3)3ab2与-2b2a.
辨一辨
下列各组中的两项是不是同类项?为什么?
一起体验成功!
下列各组中的两项是不是同类项?
(1)3xy与 yx;
(2)2a2b与2ab2;
(3)-2.1与
(4)2a与2ab.
温馨提示:所有的常数都是同类项;同类项与系数无关,与字母的排列顺序无关.
2.同类项与系数大小无关.
3.同类项与它们所含相同字母的 顺序无关.
怎样判断同类项?
1.同类项有两个标准
(1)所含字母相同;
(2)相同字母的指数分别相同.
1.指出下列多项式中的同类项:
练一练
⑵ -3x2y3 与2x2____;
⑶ 2m___ 与 -5n2____.
⑴ -3a____与 6b___;
2.请你在下面的横线上填上适当的内容,使两个单项式构成同类项.
b
a
n2
m
y3
ab2
4ab2
+
=
(__+__ )ab2
1
4
=5ab2
运用加法交换律、结合律以及乘法对于加法的分配律,同类项可以合并成一项,这称为合并同类项.
合并同类项法则:
把同类项的系数相加,所得结果作为系数,
字母和字母的次数不变.
1.下列各题合并同类项的结果对不对?
(1)a+a=2a;
(2)3a+2b=5ab;
(3)5a2-3a2=2;
(4)3x2+2x3=5x5;
(5)4x2y-5xy2=-x2y.
√
×
×
×
×
做一做
-3a+2a=-1;
7ab-7ba=0.
2.下列合并同类项是否正确
合并同
类项要
注意什
么问题?
试一试
例1: 合并同类项
4a2 + 3b2 -2ab – 3a2 + b2
=(4a2 – 3a2) -2ab + (3b2 + b2)
=(4-3)a2 – 2ab + (3+1)b2
=a2-2ab + 4b2.
做一做
例2:求代数式 的值,
5x2-2x-4+2x-4x2
其中 x=-2.
如何计算呢?
解:5x2-2x-4+2x-4x2
=(5-4)x2+(-2+2)x-4
=x2-4.
当x=-2时,
原式=(- 2)2-4=0.
注 意:
2.合并同类项只是系数相加,字母与字母的次数不变.
1.不是同类项的项不能合并!
3.合并同类项系数相加时, 系数带符号.
挑战自我
2.合并同类项mx2+4x+x2+3x-5 (m为常数)时, 若结果中不含x2项,则m=_____.
1.下列各组中,不是同类项的是( ).
A. x2y与yx2 B. 3ab2与7a2b2
C. 3abc与-abc D. 8与-8
3.单项式-xa+bya-1与3x2y的和是一个单项式, 则a=____,b=____.
B
-1
2
0
已知多项式ax+bx合并后为0,则下列说法正确的是( )
A. a=b=0 B. a=b=x=0
C. a-b=0 D. a+b=0
2. 若 与 是同类项,则a+b=_____.
考考你
如图所示是2010年8月份的日历:
星期一 二 三 四 五 六 日
2 3 4 5 6 7 8
1
9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28 29
用一个长方形框在日历中,任意圈出四个数,其和为36,你能猜出这四天分别是几号吗
a
a+1
a+7
a+8
30 31
学到了什么
同 类 项
合并同类项
两个标准
法则
(1)所含字母相同;
(2)相同字母的指数分别相同.
(1)系数相加作为
结果的系数;
(2)字母与字母的
指数不变.
再 见 碑
沪科版七年级上册
如图,在长为a,宽为b的长方形空地的中
间,有一块长为 ,宽为 的长方形
花圃,而长方形空地的其余地方种了草.
试问:草地的面积是多少?
a
b
草地的面积为
利用乘法分配律,得
因此草地的面积是
都含有字母 a、b,并且 a、b 的指数都是1.
像ab , 这样,所含字母相同,并且相同字母的次数也分别相同,叫做同类项.
1.所含字母相同;
2.相同字母的指数也相同;
3.几个常数项也是同类项.
同类项
同类项要素:
(1)各项中所含的字母相同.
(2)相同字母的指数相同.
(1)3ab与-2abc;
(2)2a2b3与-3a3b2;
(3)3ab2与-2b2a.
辨一辨
下列各组中的两项是不是同类项?为什么?
一起体验成功!
下列各组中的两项是不是同类项?
(1)3xy与 yx;
(2)2a2b与2ab2;
(3)-2.1与
(4)2a与2ab.
温馨提示:所有的常数都是同类项;同类项与系数无关,与字母的排列顺序无关.
2.同类项与系数大小无关.
3.同类项与它们所含相同字母的 顺序无关.
怎样判断同类项?
1.同类项有两个标准
(1)所含字母相同;
(2)相同字母的指数分别相同.
1.指出下列多项式中的同类项:
练一练
⑵ -3x2y3 与2x2____;
⑶ 2m___ 与 -5n2____.
⑴ -3a____与 6b___;
2.请你在下面的横线上填上适当的内容,使两个单项式构成同类项.
b
a
n2
m
y3
ab2
4ab2
+
=
(__+__ )ab2
1
4
=5ab2
运用加法交换律、结合律以及乘法对于加法的分配律,同类项可以合并成一项,这称为合并同类项.
合并同类项法则:
把同类项的系数相加,所得结果作为系数,
字母和字母的次数不变.
1.下列各题合并同类项的结果对不对?
(1)a+a=2a;
(2)3a+2b=5ab;
(3)5a2-3a2=2;
(4)3x2+2x3=5x5;
(5)4x2y-5xy2=-x2y.
√
×
×
×
×
做一做
-3a+2a=-1;
7ab-7ba=0.
2.下列合并同类项是否正确
合并同
类项要
注意什
么问题?
试一试
例1: 合并同类项
4a2 + 3b2 -2ab – 3a2 + b2
=(4a2 – 3a2) -2ab + (3b2 + b2)
=(4-3)a2 – 2ab + (3+1)b2
=a2-2ab + 4b2.
做一做
例2:求代数式 的值,
5x2-2x-4+2x-4x2
其中 x=-2.
如何计算呢?
解:5x2-2x-4+2x-4x2
=(5-4)x2+(-2+2)x-4
=x2-4.
当x=-2时,
原式=(- 2)2-4=0.
注 意:
2.合并同类项只是系数相加,字母与字母的次数不变.
1.不是同类项的项不能合并!
3.合并同类项系数相加时, 系数带符号.
挑战自我
2.合并同类项mx2+4x+x2+3x-5 (m为常数)时, 若结果中不含x2项,则m=_____.
1.下列各组中,不是同类项的是( ).
A. x2y与yx2 B. 3ab2与7a2b2
C. 3abc与-abc D. 8与-8
3.单项式-xa+bya-1与3x2y的和是一个单项式, 则a=____,b=____.
B
-1
2
0
已知多项式ax+bx合并后为0,则下列说法正确的是( )
A. a=b=0 B. a=b=x=0
C. a-b=0 D. a+b=0
2. 若 与 是同类项,则a+b=_____.
考考你
如图所示是2010年8月份的日历:
星期一 二 三 四 五 六 日
2 3 4 5 6 7 8
1
9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28 29
用一个长方形框在日历中,任意圈出四个数,其和为36,你能猜出这四天分别是几号吗
a
a+1
a+7
a+8
30 31
学到了什么
同 类 项
合并同类项
两个标准
法则
(1)所含字母相同;
(2)相同字母的指数分别相同.
(1)系数相加作为
结果的系数;
(2)字母与字母的
指数不变.
再 见 碑
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
