3.2 一元一次方程的应用(第1课时) 课件(共21张PPT)
文档属性
| 名称 | 3.2 一元一次方程的应用(第1课时) 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 918.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 09:54:18 | ||
图片预览







文档简介
(共21张PPT)
引入:
我们学习解方程的目的是为了应用!
请同学们思考:
我们学习解方程的目的是什么?
列方程解应用题
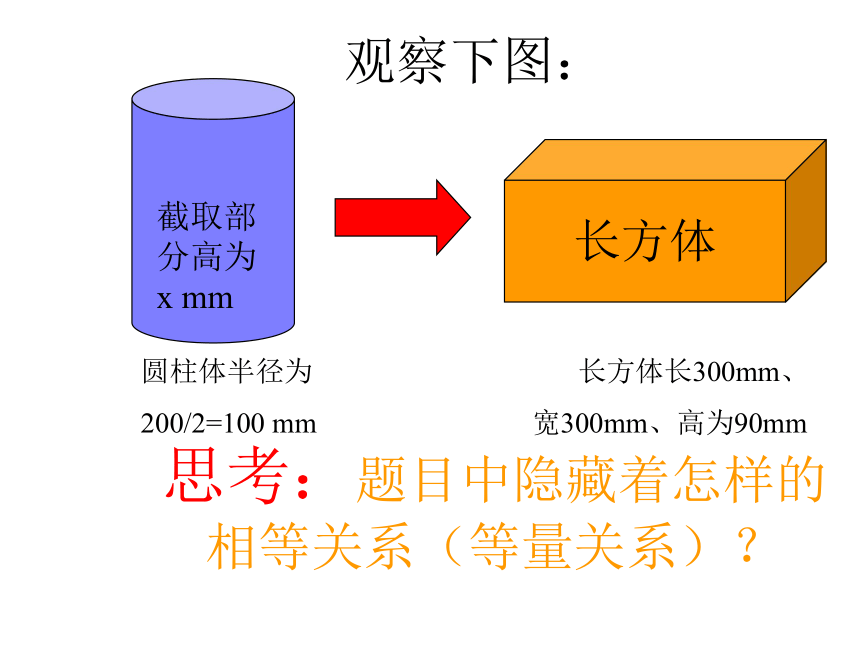
例1 用直径为200mm的圆柱体钢,锻造一个长、宽、高分别是300mm、300mm和90mm的长方体毛坯,至少应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
几何体问题
思考:题目中隐藏着怎样的相等关系(等量关系)?
截取部分高为x mm
长方体
观察下图:
圆柱体半径为 长方体长300mm、
200/2=100 mm 宽300mm、高为90mm
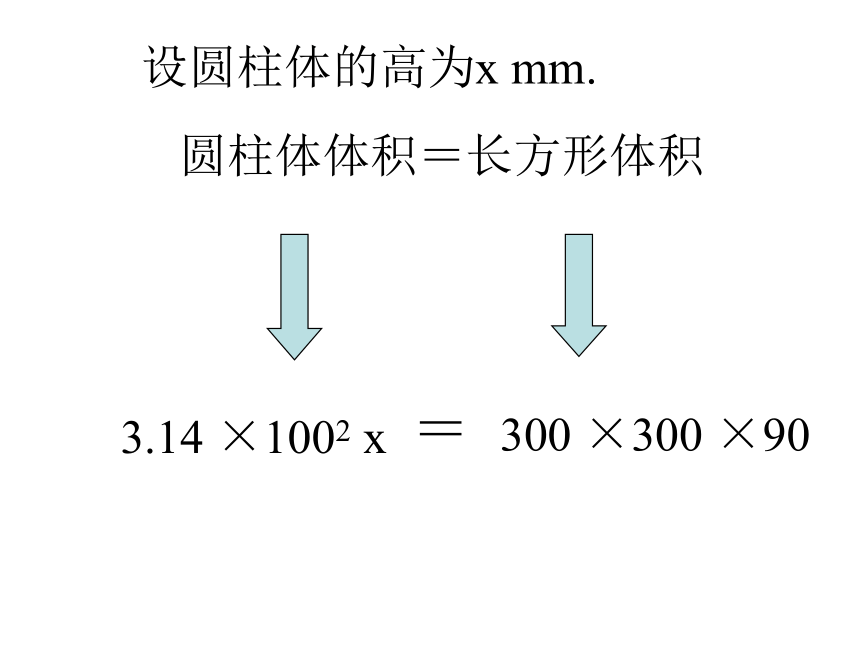
圆柱体体积=长方形体积
=
3.14 ×1002 x
300 ×300 ×90
设圆柱体的高为x mm.
解:设至少要截取圆柱体钢X mm,
根据题意,得
答:至少应截圆柱体钢长约为258mm.
3.14 ×1002 x =300 ×300 ×90.
解得x≈258.
(注意:此题结果不是四舍五入.)
行程问题中速度、时
间、路程三者之间的关系:
路程=速度×时间;
速度=路程/时间;
时间=路程/速度.
小张和父亲预定搭乘家门口的公共汽车赶往火车站,去家乡看望爷爷。在行驶了1/3路程时,小张向司机询问到达火车站的时间,司机估计继续乘公共汽车到火车站时火车将正好开出,根据司机的建议,小张和父亲随即下车改乘出租车,车速提高了一倍,结果赶在火车开车前45分钟到达火车站,已知公共汽车的平均速度是40千米/时.
问小张家到火车站有多远?
题 中 有 哪 些 等 量 关 系?
不换车使用的时间 - 换车使用的时间
= 提前时间
解:设乘公共汽车实际上行驶了x千 米,由题意,得
解得
经检验,x=30符合题意.
答:小张家到火车站有90千米.
是否有其他设未知数
的方法?
设时间为未知数行吗?
对于一些实际问题,我们可以从不同的角度寻找相等关系,设出合适的未知数,列出不同的方程来解.
试试看
设:公共汽车实际行驶x小时
x小时
2x小时
x小时
公共汽车
出租车
时 间
(h)
时 间
(h)
速 度(km/h)
速 度
(km/h)
80
40
换车
40
40
不换车
全程的后2/3
全程的1/3
x
x
2x
解法2:
解得:
答:小张家到火车站有90千米.
设公共汽车实际行驶x小时,根据题意,得
经检验,它符合题意.
议一议
1、上述几种解法有什么不同?
2、在解行程问题时可借助那些
方法解题?
在解应用题时通常有二种设法:
在解行程问题时通常借助什么进行解题?
直接设法与间接设法.
行程图与列表.
列一元一次方程解应用题的步骤有哪些?
应认真审题,分析题中的数量关系,用字母表示题目中的未知数时一般采用直接设法,当直接设法使列方程有困难可采用间接设法,注意未知数的单位不要漏写.
可借助图表分析题中的已知量和未知量之间关系,列出等式两边的代数式,注意它们的量要一致,使它们都表示一个相等或相同的量.
(1)设未知数
(2)寻找等量关系
议一议
方程的变形应根据等式性质和运算法则.
检查方程的解是否符合应用题的实际意义,进行取舍,并注意单位.
(4)解方程
(5)写出答案
列方程应满足三个条件:各类是同类量,单位一致,两边是等量.
(3)列方程
1、为庆祝校运会开幕,七年级(2)班接受了制作小旗的任务,原计划一半同学参加制作,每天制作40面,完成了二分之一以后,全班同学一起参加,结果比原计划提前一天半完成任务,假设每人的制作效率相同,问共制作小旗多少面?
设:共制作小旗x面
解得:
答:共制作小旗480面.
2、 小明每天早上要在7:30分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他,问爸爸追上小明用了多长时间
则有5×80+80X=180X
追上
小明5分钟走的路程
小明在爸爸追时走的路程
爸爸追赶小明时走的路程
追上时,距学校还有多远
解得X=4
280千米
家
学校
点滴收获
实际问题
数学问题的解
实际问题
的答案
数学问题
(一元一次方程)
设未知数,列方程
解方程
检验
我知道了……
我感到困难是……
引入:
我们学习解方程的目的是为了应用!
请同学们思考:
我们学习解方程的目的是什么?
列方程解应用题
例1 用直径为200mm的圆柱体钢,锻造一个长、宽、高分别是300mm、300mm和90mm的长方体毛坯,至少应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
几何体问题
思考:题目中隐藏着怎样的相等关系(等量关系)?
截取部分高为x mm
长方体
观察下图:
圆柱体半径为 长方体长300mm、
200/2=100 mm 宽300mm、高为90mm
圆柱体体积=长方形体积
=
3.14 ×1002 x
300 ×300 ×90
设圆柱体的高为x mm.
解:设至少要截取圆柱体钢X mm,
根据题意,得
答:至少应截圆柱体钢长约为258mm.
3.14 ×1002 x =300 ×300 ×90.
解得x≈258.
(注意:此题结果不是四舍五入.)
行程问题中速度、时
间、路程三者之间的关系:
路程=速度×时间;
速度=路程/时间;
时间=路程/速度.
小张和父亲预定搭乘家门口的公共汽车赶往火车站,去家乡看望爷爷。在行驶了1/3路程时,小张向司机询问到达火车站的时间,司机估计继续乘公共汽车到火车站时火车将正好开出,根据司机的建议,小张和父亲随即下车改乘出租车,车速提高了一倍,结果赶在火车开车前45分钟到达火车站,已知公共汽车的平均速度是40千米/时.
问小张家到火车站有多远?
题 中 有 哪 些 等 量 关 系?
不换车使用的时间 - 换车使用的时间
= 提前时间
解:设乘公共汽车实际上行驶了x千 米,由题意,得
解得
经检验,x=30符合题意.
答:小张家到火车站有90千米.
是否有其他设未知数
的方法?
设时间为未知数行吗?
对于一些实际问题,我们可以从不同的角度寻找相等关系,设出合适的未知数,列出不同的方程来解.
试试看
设:公共汽车实际行驶x小时
x小时
2x小时
x小时
公共汽车
出租车
时 间
(h)
时 间
(h)
速 度(km/h)
速 度
(km/h)
80
40
换车
40
40
不换车
全程的后2/3
全程的1/3
x
x
2x
解法2:
解得:
答:小张家到火车站有90千米.
设公共汽车实际行驶x小时,根据题意,得
经检验,它符合题意.
议一议
1、上述几种解法有什么不同?
2、在解行程问题时可借助那些
方法解题?
在解应用题时通常有二种设法:
在解行程问题时通常借助什么进行解题?
直接设法与间接设法.
行程图与列表.
列一元一次方程解应用题的步骤有哪些?
应认真审题,分析题中的数量关系,用字母表示题目中的未知数时一般采用直接设法,当直接设法使列方程有困难可采用间接设法,注意未知数的单位不要漏写.
可借助图表分析题中的已知量和未知量之间关系,列出等式两边的代数式,注意它们的量要一致,使它们都表示一个相等或相同的量.
(1)设未知数
(2)寻找等量关系
议一议
方程的变形应根据等式性质和运算法则.
检查方程的解是否符合应用题的实际意义,进行取舍,并注意单位.
(4)解方程
(5)写出答案
列方程应满足三个条件:各类是同类量,单位一致,两边是等量.
(3)列方程
1、为庆祝校运会开幕,七年级(2)班接受了制作小旗的任务,原计划一半同学参加制作,每天制作40面,完成了二分之一以后,全班同学一起参加,结果比原计划提前一天半完成任务,假设每人的制作效率相同,问共制作小旗多少面?
设:共制作小旗x面
解得:
答:共制作小旗480面.
2、 小明每天早上要在7:30分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他,问爸爸追上小明用了多长时间
则有5×80+80X=180X
追上
小明5分钟走的路程
小明在爸爸追时走的路程
爸爸追赶小明时走的路程
追上时,距学校还有多远
解得X=4
280千米
家
学校
点滴收获
实际问题
数学问题的解
实际问题
的答案
数学问题
(一元一次方程)
设未知数,列方程
解方程
检验
我知道了……
我感到困难是……
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
