3.2一元一次方程的应用 第1课时 课件(共22张PPT)
文档属性
| 名称 | 3.2一元一次方程的应用 第1课时 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 09:40:52 | ||
图片预览







文档简介
(共22张PPT)
3.2 一元一次方程的应用
第1课时
h
R
要想求出某个同学的体积是多少?你怎么测量呢?
你还能举出相类似的事例吗?
(古代:曹冲称象)
形状改变,
体积不变.
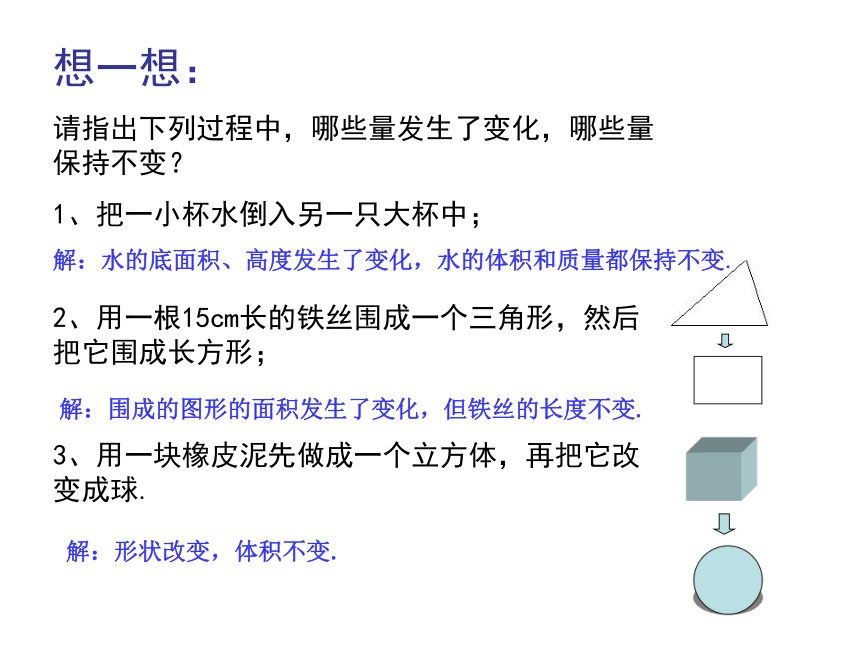
想一想:
请指出下列过程中,哪些量发生了变化,哪些量保持不变?
1、把一小杯水倒入另一只大杯中;
2、用一根15cm长的铁丝围成一个三角形,然后把它围成长方形;
3、用一块橡皮泥先做成一个立方体,再把它改变成球.
解:水的底面积、高度发生了变化,水的体积和质量都保持不变.
解:围成的图形的面积发生了变化,但铁丝的长度不变.
解:形状改变,体积不变.
例1 一纪念碑建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问纪念碑建筑底面的边长是多少米
x
3
3
分析:如图,若用x表示中间空白正方形的边长,本题的等量关系是什么?
阴影部分的面积=192块边长为0.75米的正方形花岗石的面积.
怎样用含x的代数式表示阴影部分的面积呢 利用练习纸中的图你能设计几种不同的计算方法.
方案如下:
方案一
方案二
方案三
方案四
答:纪念碑建筑底面的边长为6米.
一纪念碑建筑的底面呈正方形,其四周铺上花岗岩,形成一个宽为3米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了192块边长为0.75米的正方形花岗岩,问纪念碑建筑底面的边长是多少米
x
3
3
方案二
阴影部分的面积=192块边长为0.75米的正方形花岗岩的面积
阴影部分的面积=4个长为(x+3)米,宽为3米的长方形的面积
解: 设纪念碑建筑底面的边长为x米,根据题意,得
解这个方程,得 x=6
本题还有哪些解法?
用直径为200厘米的钢柱锻造一块长、宽、高分别为300厘米,300厘米,90厘米的长方体毛坯底板,应截取圆柱多少长?(圆柱的体积=底面积×高.计算时,π取3.14,要求结果精确到0.1厘米)
例2
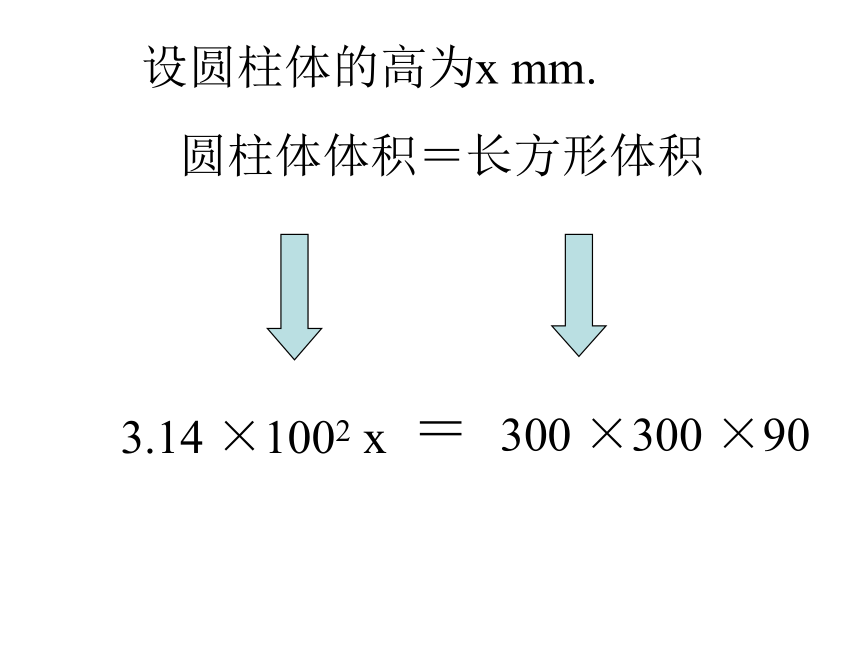
圆柱体体积=长方形体积
=
3.14 ×1002 x
300 ×300 ×90
设圆柱体的高为x mm.
解:设至少要截取圆柱体钢X mm,
根据题意,得
答:至少应截圆柱体钢长约为258mm.
3.14 ×1002 x =300 ×300 ×90.
解得x≈258.
(注意:此题结果不是四舍五入.)
1、在应用方程解决有关实际问题时,清楚地分辨量之间的关系,尤其是相等关系是建立方程的关键.
2、解题中的检验对确保答案的正确和合理很有帮助,但具体过程可省略不写.
3、对于等积变形问题,它的基本数量关系是相关的面积公式,相等关系的特征是存在不变量,也就是用不同的方法来计算阴影部分的面积,面积不变.
总一总
速度、时间、路程之间的关系:
速度×时间=路程
什么时候才能相遇?
例1 小明与小兵的加分别在相距20km的甲、乙两地,星期天小明从家里出发骑自行车去小兵家,小明骑车的速度为13km/h.两人商定小兵到时候从家里出发骑自行车去接小明,小兵骑车速度是12km/h.
(1)如果两人同时出发,那么他们经过多少小时相遇?
(2)如果小明先走30分钟,那么小兵要走多少小时才能与小明相遇?
等量关系
如果两人同时出发,则
小明走的路程+小兵走的路程=甲、乙两地之间的距离
如果小明先走30分钟,则
小明先走的路程+小兵出发后小明走的路程+小兵走的路程=甲、乙两地之间的距离
解 (1)设小明与小兵骑车走了x h后相遇,那么
小明骑车走的路程为13x km,
小兵骑车走的路程为12x km.
根据题意,建立方程为13x+12x=20.
解这个方程得 x=0.8.
(2)设小兵骑车走了x h后与小明相遇,那么
小兵骑车走的路程为 12x km,
小明骑车走的路程为(13×0.5+13x) km.
根据题意,建立方程为 12x+(13×0.5+13x)=20.
解这个方程,得 x=0.54.
答:(1)两人骑车走了0.8 h相遇;(2)小兵骑车走了0.54 h后与小明相遇.
学校距雷锋纪念馆多
例2 小斌和小强骑自行车从学校出发去雷锋纪念馆参观,出发前他俩一起算了一下:如果每小时骑10 km,上午10时才能到达;如果每小时骑15 km,则上午9时30分便可到达.
你能算出他们的学校到雷锋纪念馆的路程吗?
速度×时间=路程
解 设他俩的学校到雷锋纪念馆的路程为s km,依题意,得
解这个方程,得 s =15.
答:小斌和小强的学校到雷锋纪念馆的路程为15 km.
列一元一次方程解应用题的步骤有哪些?
应认真审题,分析题中的数量关系,用字母表示题目中的未知数时一般采用直接设法,当直接设法使列方程有困难可采用间接设法,注意未知数的单位不要漏写.
可借助图表分析题中的已知量和未知量之间关系,列出等式两边的代数式,注意它们的量要一致,使它们都表示一个相等或相同的量.
(1)设未知数
(2)寻找等量关系
方程的变形应根据等式性质和运算法则.
检查方程的解是否符合应用题的实际意义,进行取舍,并注意单位.
(4)解方程
(5)写出答案
列方程应满足三个条件:各类是同类量,单位一致,两边是等量.
(3)列方程
如图,一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少?
30cm
20cm
一队学生步行去郊外春游,每小时走4 km.学生甲因为有事迟出发30分钟,为了赶上队伍,以6 km/h 的速度追赶,问该生用多少时间追上了队伍?
点滴收获
实际问题
数学问题的解
实际问题
的答案
数学问题
(一元一次方程)
设未知数,列方程
解方程
检验
再 见
3.2 一元一次方程的应用
第1课时
h
R
要想求出某个同学的体积是多少?你怎么测量呢?
你还能举出相类似的事例吗?
(古代:曹冲称象)
形状改变,
体积不变.
想一想:
请指出下列过程中,哪些量发生了变化,哪些量保持不变?
1、把一小杯水倒入另一只大杯中;
2、用一根15cm长的铁丝围成一个三角形,然后把它围成长方形;
3、用一块橡皮泥先做成一个立方体,再把它改变成球.
解:水的底面积、高度发生了变化,水的体积和质量都保持不变.
解:围成的图形的面积发生了变化,但铁丝的长度不变.
解:形状改变,体积不变.
例1 一纪念碑建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问纪念碑建筑底面的边长是多少米
x
3
3
分析:如图,若用x表示中间空白正方形的边长,本题的等量关系是什么?
阴影部分的面积=192块边长为0.75米的正方形花岗石的面积.
怎样用含x的代数式表示阴影部分的面积呢 利用练习纸中的图你能设计几种不同的计算方法.
方案如下:
方案一
方案二
方案三
方案四
答:纪念碑建筑底面的边长为6米.
一纪念碑建筑的底面呈正方形,其四周铺上花岗岩,形成一个宽为3米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了192块边长为0.75米的正方形花岗岩,问纪念碑建筑底面的边长是多少米
x
3
3
方案二
阴影部分的面积=192块边长为0.75米的正方形花岗岩的面积
阴影部分的面积=4个长为(x+3)米,宽为3米的长方形的面积
解: 设纪念碑建筑底面的边长为x米,根据题意,得
解这个方程,得 x=6
本题还有哪些解法?
用直径为200厘米的钢柱锻造一块长、宽、高分别为300厘米,300厘米,90厘米的长方体毛坯底板,应截取圆柱多少长?(圆柱的体积=底面积×高.计算时,π取3.14,要求结果精确到0.1厘米)
例2
圆柱体体积=长方形体积
=
3.14 ×1002 x
300 ×300 ×90
设圆柱体的高为x mm.
解:设至少要截取圆柱体钢X mm,
根据题意,得
答:至少应截圆柱体钢长约为258mm.
3.14 ×1002 x =300 ×300 ×90.
解得x≈258.
(注意:此题结果不是四舍五入.)
1、在应用方程解决有关实际问题时,清楚地分辨量之间的关系,尤其是相等关系是建立方程的关键.
2、解题中的检验对确保答案的正确和合理很有帮助,但具体过程可省略不写.
3、对于等积变形问题,它的基本数量关系是相关的面积公式,相等关系的特征是存在不变量,也就是用不同的方法来计算阴影部分的面积,面积不变.
总一总
速度、时间、路程之间的关系:
速度×时间=路程
什么时候才能相遇?
例1 小明与小兵的加分别在相距20km的甲、乙两地,星期天小明从家里出发骑自行车去小兵家,小明骑车的速度为13km/h.两人商定小兵到时候从家里出发骑自行车去接小明,小兵骑车速度是12km/h.
(1)如果两人同时出发,那么他们经过多少小时相遇?
(2)如果小明先走30分钟,那么小兵要走多少小时才能与小明相遇?
等量关系
如果两人同时出发,则
小明走的路程+小兵走的路程=甲、乙两地之间的距离
如果小明先走30分钟,则
小明先走的路程+小兵出发后小明走的路程+小兵走的路程=甲、乙两地之间的距离
解 (1)设小明与小兵骑车走了x h后相遇,那么
小明骑车走的路程为13x km,
小兵骑车走的路程为12x km.
根据题意,建立方程为13x+12x=20.
解这个方程得 x=0.8.
(2)设小兵骑车走了x h后与小明相遇,那么
小兵骑车走的路程为 12x km,
小明骑车走的路程为(13×0.5+13x) km.
根据题意,建立方程为 12x+(13×0.5+13x)=20.
解这个方程,得 x=0.54.
答:(1)两人骑车走了0.8 h相遇;(2)小兵骑车走了0.54 h后与小明相遇.
学校距雷锋纪念馆多
例2 小斌和小强骑自行车从学校出发去雷锋纪念馆参观,出发前他俩一起算了一下:如果每小时骑10 km,上午10时才能到达;如果每小时骑15 km,则上午9时30分便可到达.
你能算出他们的学校到雷锋纪念馆的路程吗?
速度×时间=路程
解 设他俩的学校到雷锋纪念馆的路程为s km,依题意,得
解这个方程,得 s =15.
答:小斌和小强的学校到雷锋纪念馆的路程为15 km.
列一元一次方程解应用题的步骤有哪些?
应认真审题,分析题中的数量关系,用字母表示题目中的未知数时一般采用直接设法,当直接设法使列方程有困难可采用间接设法,注意未知数的单位不要漏写.
可借助图表分析题中的已知量和未知量之间关系,列出等式两边的代数式,注意它们的量要一致,使它们都表示一个相等或相同的量.
(1)设未知数
(2)寻找等量关系
方程的变形应根据等式性质和运算法则.
检查方程的解是否符合应用题的实际意义,进行取舍,并注意单位.
(4)解方程
(5)写出答案
列方程应满足三个条件:各类是同类量,单位一致,两边是等量.
(3)列方程
如图,一个铁片长30cm,宽20cm,打算从四个角各截去一个小正方形,然后把四边折起来做一个无盖的铁盒,铁盒的底面周长为60cm,问铁盒的高是多少?
30cm
20cm
一队学生步行去郊外春游,每小时走4 km.学生甲因为有事迟出发30分钟,为了赶上队伍,以6 km/h 的速度追赶,问该生用多少时间追上了队伍?
点滴收获
实际问题
数学问题的解
实际问题
的答案
数学问题
(一元一次方程)
设未知数,列方程
解方程
检验
再 见
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
