3.5三元一次方程组及其解法 课件(共18张PPT)
文档属性
| 名称 | 3.5三元一次方程组及其解法 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 741.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 09:43:10 | ||
图片预览

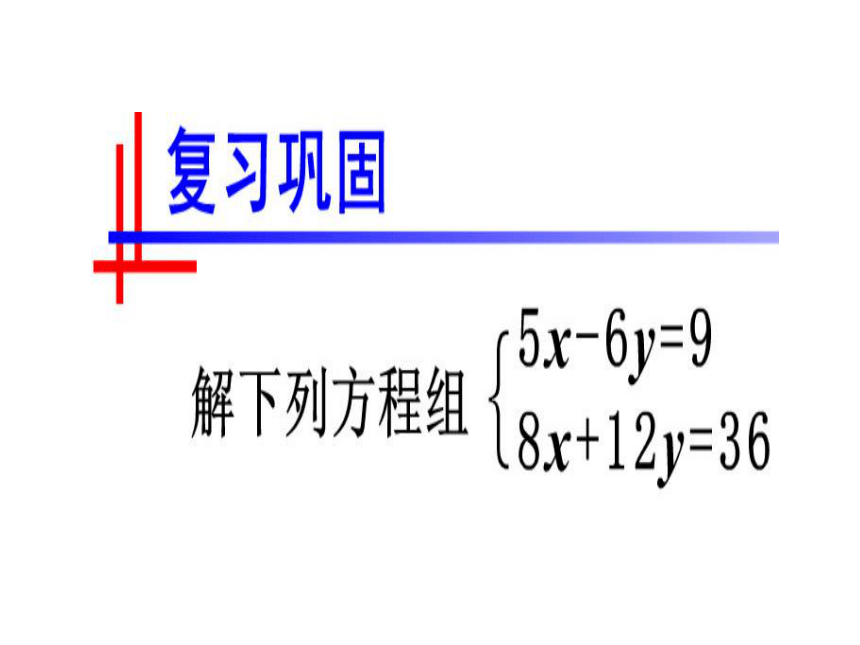





文档简介
(共18张PPT)
沪科版七年级(上册)
前面我们学习了二元一次方程组及
其解法——消元法。对于有两个未知数
的问题,可以列出二元一次方程组来解
决。实际上,在我们的学习和生活中会
遇到不少含有更多未知数的问题。
如本章的“数学史话”所介绍的《九章算术》一书中第八章第一题,列成方程组就是
3x +2 y + z = 39,
2x +3y + z = 34,
x + 2y + 3z = 26.
{
这种由三个一次方程组成的含三个未知数的方程组,叫做三元一次方程组。
观察方程组:
如何解三元一次方程组?
①
②
③
3x +2 y + z = 39,
2x +3y + z = 34,
x + 2y + 3z = 26.
{
我们仍可把它进行“消元”,即“三元”化为“二元”,“二元”化为“一元”
解三元一次方程组的基本思路与解二元一次方程组的基本思路一样,即
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
例 解三元一次方程组
x + y +2z = 3 ①
-2x - y + z = -3 ②
x + 2y - 4z = -5 ③
{
分析:可先用加减消元法消去x,得到一个只含y、z二元一次方程组
解:②+ ① ×2 ,得
y+ 5z = 3 ④
③ - ①,得
y + 5z = 3
y + 6z = -8
{
解这个方程组,得
y=-2
z=1
{
把y=-2,z=1代入① ,得x=3
因此,三元一次方程组的解为
{
你还有其他解法吗?试一试,并与这种解法进行比较.
y - 6z = -8 ⑤
④与⑤联立成二元一次方程组:
x=3
y=-2
z=1
上面的解法是先通过消元,消去②和③中的x,将方程组化成
y + 5z = 3 ④
y + 6z = -8 ⑤
x + y +2z = 3 ①
{
x + y +2z = 3 ①
y + 5z = 3 ④
11z = 11 ⑥
{
最后得出z,再将z代入④ ,解出y,最后将y、z代回①解出x。
再通过消元,消去⑤中的y,化成
像上面,通过消元,把一个较复杂的三元一次方程组化为简单易解的形如① ④ ⑥联立成的阶梯型方程组,从而通过回代得出其解,整个求解的过程就称为用消元法解三元一次方程组。
解三元一次方程组
3x +2 y + z = 39 ①
2x -3 y + z = 34 ②
X + 2y + 3z = 26 ③
你能把它化成与前面类似的阶梯型方程组吗?
自己来动手试一试吧!
{
小明手头有12张面额分别是1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元的纸币各多少张?
提出问题:1.题目中有几个条件?
2.问题中有几个未知量?
3.根据等量关系你能列出方程组吗?
1元
2元
5元
合 计
注
分析:在本题中,有三个未知数,我们可设1元、2
元、5元的纸币分别是x张、y张、 z张,用表
格表示三个量之间的关系如下:
x
y
z
x
2y
5z
12
22
1元纸币的数量是2元纸币数量的4倍,即x=4y
解:设1元、2元、5元的纸币分别为x张、y
张、z张。
根据题意,得:
x = 8
y = 2
z = 2
解得
{
{
x + y + z = 12
x = 4y
x + 2y + 5z = 22
答:1元的纸币有8张,2元的纸币有2张,5元的纸币有2张。
解三元一次方程组的基本思路是:
通过“代入”或“加减”进行 ,
把 转化为 ,使解三元一次方
程组转化为解 ,进而再转化为
解 。
消元
“三元”
“二元”
二元一次方程组
一元一次方程
在消去一个未知数转化成二元一次方程组的问题上,有什么技巧吗?谈谈你的想法。
再 见
沪科版七年级(上册)
前面我们学习了二元一次方程组及
其解法——消元法。对于有两个未知数
的问题,可以列出二元一次方程组来解
决。实际上,在我们的学习和生活中会
遇到不少含有更多未知数的问题。
如本章的“数学史话”所介绍的《九章算术》一书中第八章第一题,列成方程组就是
3x +2 y + z = 39,
2x +3y + z = 34,
x + 2y + 3z = 26.
{
这种由三个一次方程组成的含三个未知数的方程组,叫做三元一次方程组。
观察方程组:
如何解三元一次方程组?
①
②
③
3x +2 y + z = 39,
2x +3y + z = 34,
x + 2y + 3z = 26.
{
我们仍可把它进行“消元”,即“三元”化为“二元”,“二元”化为“一元”
解三元一次方程组的基本思路与解二元一次方程组的基本思路一样,即
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
例 解三元一次方程组
x + y +2z = 3 ①
-2x - y + z = -3 ②
x + 2y - 4z = -5 ③
{
分析:可先用加减消元法消去x,得到一个只含y、z二元一次方程组
解:②+ ① ×2 ,得
y+ 5z = 3 ④
③ - ①,得
y + 5z = 3
y + 6z = -8
{
解这个方程组,得
y=-2
z=1
{
把y=-2,z=1代入① ,得x=3
因此,三元一次方程组的解为
{
你还有其他解法吗?试一试,并与这种解法进行比较.
y - 6z = -8 ⑤
④与⑤联立成二元一次方程组:
x=3
y=-2
z=1
上面的解法是先通过消元,消去②和③中的x,将方程组化成
y + 5z = 3 ④
y + 6z = -8 ⑤
x + y +2z = 3 ①
{
x + y +2z = 3 ①
y + 5z = 3 ④
11z = 11 ⑥
{
最后得出z,再将z代入④ ,解出y,最后将y、z代回①解出x。
再通过消元,消去⑤中的y,化成
像上面,通过消元,把一个较复杂的三元一次方程组化为简单易解的形如① ④ ⑥联立成的阶梯型方程组,从而通过回代得出其解,整个求解的过程就称为用消元法解三元一次方程组。
解三元一次方程组
3x +2 y + z = 39 ①
2x -3 y + z = 34 ②
X + 2y + 3z = 26 ③
你能把它化成与前面类似的阶梯型方程组吗?
自己来动手试一试吧!
{
小明手头有12张面额分别是1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元的纸币各多少张?
提出问题:1.题目中有几个条件?
2.问题中有几个未知量?
3.根据等量关系你能列出方程组吗?
1元
2元
5元
合 计
注
分析:在本题中,有三个未知数,我们可设1元、2
元、5元的纸币分别是x张、y张、 z张,用表
格表示三个量之间的关系如下:
x
y
z
x
2y
5z
12
22
1元纸币的数量是2元纸币数量的4倍,即x=4y
解:设1元、2元、5元的纸币分别为x张、y
张、z张。
根据题意,得:
x = 8
y = 2
z = 2
解得
{
{
x + y + z = 12
x = 4y
x + 2y + 5z = 22
答:1元的纸币有8张,2元的纸币有2张,5元的纸币有2张。
解三元一次方程组的基本思路是:
通过“代入”或“加减”进行 ,
把 转化为 ,使解三元一次方
程组转化为解 ,进而再转化为
解 。
消元
“三元”
“二元”
二元一次方程组
一元一次方程
在消去一个未知数转化成二元一次方程组的问题上,有什么技巧吗?谈谈你的想法。
再 见
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
