4.5.角的比较与补(余)角 课件(共16张PPT)
文档属性
| 名称 | 4.5.角的比较与补(余)角 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 659.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 14:20:10 | ||
图片预览





文档简介
(共16张PPT)
度量法、叠合法
你能将图中扇子张开的角度按从大到小排列吗?
①
②
③
④
②>④>③> ①
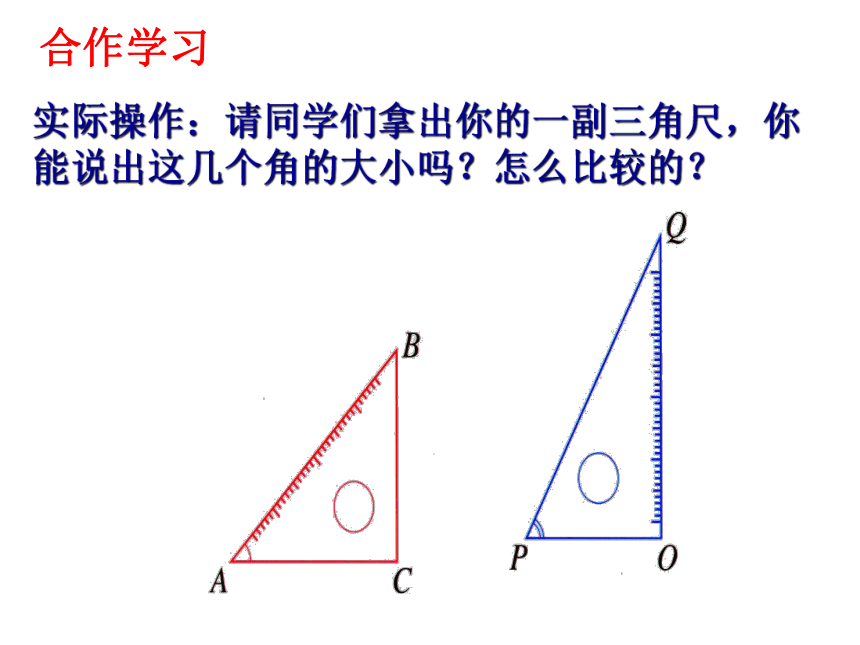
实际操作:请同学们拿出你的一副三角尺,你能说出这几个角的大小吗?怎么比较的?
合作学习
方法一:叠合法
把一个角放到另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在这一条边的同侧.
此时:AB边落在 的内部,表明:
问:若AB边与PQ边重合表明什么
问:若AB边落在PQ边的外部又表明什么?
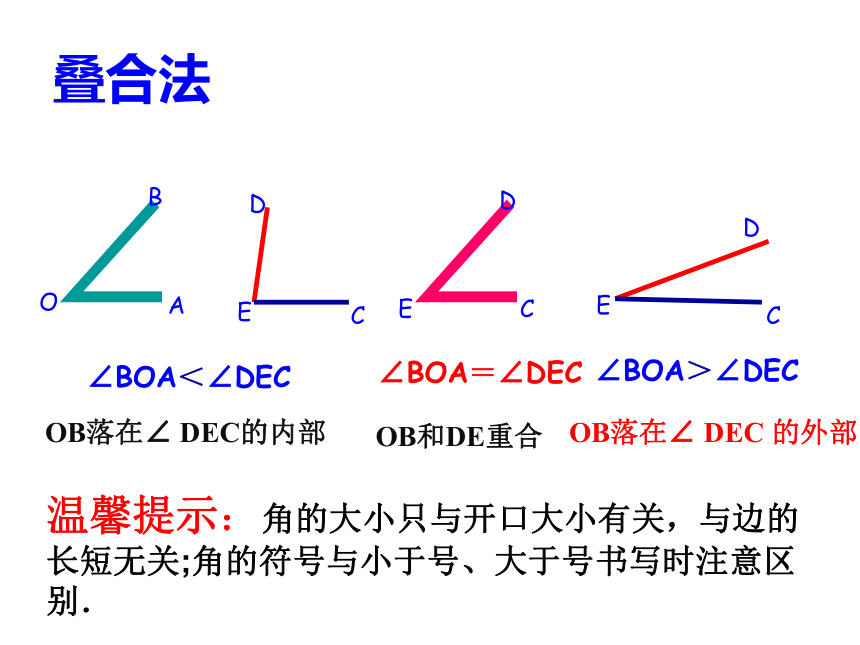
叠合法
∠
∠
E
C
D
O
A
B
E
D
C
E
C
D
∠BOA<∠DEC
∠BOA=∠DEC
∠BOA>∠DEC
OB和DE重合
OB落在∠ DEC的内部
OB落在∠ DEC 的外部
温馨提示:角的大小只与开口大小有关,与边的长短无关;角的符号与小于号、大于号书写时注意区别.
方法二:度量法
小学我们学过用量角器测量一个角,角的大小也可以按其度数比较,度数大的角则大,度数小的则小.反之,角大度数大,角小度数小.
注意:使用量角器应注意的问题.即三点:对中、重合、读数.
如:
请用量角器量出你的一副三角尺中各个角的度数.
1、请同学们同桌两人分别画两个角,然后交换用量角器测量其度数,比较它们的大小.
量一量,比一比
2、观察下图中的∠AOC,∠COB和∠AOB ,如何表示它们的关系.
∠AOC+∠COB=∠AOB
∠AOB-∠AOC=∠COB
∠AOB-∠COB=∠AOC
1、下列说法正确的是( )
A,角的边越长,则角越大
B,角的大小与边的长短无关
C,角的大小与顶点的位置有关
D,角的大小决定于始边旋转的方向
B
2、下图一组角,其大小顺序正确的是( )
A, ∠1< ∠2< ∠3< ∠4 B, ∠1< ∠4< ∠2< ∠3
C, ∠1< ∠4< ∠3< ∠2 D, ∠1< ∠3< ∠2<∠4
D
∠
1
2
3
4
选一选:
例 如图,求解下列问题:
(1)比较∠AOC 与∠BOC,∠BOD与∠COD的大小.
(2)将∠AOC 写成两个角的和或两个角的差的形式.
O
D
A
C
解:(1)由图可以看出:
(2)∠AOC=∠AOB+∠BOC
∠AOC>∠BOC,(OB在∠AOC 内)
∠BOD>∠COD,(OC在∠BOD 内)
B
∠AOC=∠AOD-∠COD
在一张透明纸上任意画一个角∠AOB,把这张纸折叠,使角的两边OA与OB重合,然后把纸展开,画出折痕OC. ∠AOC与∠BOC之间有怎样的大小关系?
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线.
O
A
B
C
如图,射线OC是∠AOB的平分线或OC平分∠AOB
则有 ∠AOC=∠BOC= ∠AOB, 或 ∠AOB=2∠AOC=2∠BOC.
合作学习
观察下图,∠ 1+ ∠ 2与Rt∠ AOB相等吗?你是怎么判断的呢?
1
2
1
2
1
A
O B
如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余.也可以说其中一个角是另一个角的余角.
如果∠1+∠2=90°,那么∠1与∠2互为余角,∠1是∠2的余角,∠2是∠1的余角.
再观察下图, ∠ 3+ ∠ 4与∠ AOB相等吗?你是怎么判断的呢?
如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角.
如上图, ∠3与∠4互为补角,∠3是∠4的补角,∠4也是∠3的补角.
互补的数量关系: ∠α+∠β=180 °
数量关系:∠3+∠4=180 °.
3
4
3
O
4
A
B
3
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等。
同角或等角的补角相等。
1
2
1
2
做一做
解 因为 ∠1+∠3=42°+48°=90°,
所以 ∠1与∠3互余.
因为 ∠1+∠2=42°+138°=180°,
所以 ∠1与∠2互补.
如图,已知∠1=42°,∠2=138°,
∠3=48°,问图中有没有互余或互补的角?
若有,请把它们写出来,并说明理由.
1
2
3
度量法、叠合法
你能将图中扇子张开的角度按从大到小排列吗?
①
②
③
④
②>④>③> ①
实际操作:请同学们拿出你的一副三角尺,你能说出这几个角的大小吗?怎么比较的?
合作学习
方法一:叠合法
把一个角放到另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在这一条边的同侧.
此时:AB边落在 的内部,表明:
问:若AB边与PQ边重合表明什么
问:若AB边落在PQ边的外部又表明什么?
叠合法
∠
∠
E
C
D
O
A
B
E
D
C
E
C
D
∠BOA<∠DEC
∠BOA=∠DEC
∠BOA>∠DEC
OB和DE重合
OB落在∠ DEC的内部
OB落在∠ DEC 的外部
温馨提示:角的大小只与开口大小有关,与边的长短无关;角的符号与小于号、大于号书写时注意区别.
方法二:度量法
小学我们学过用量角器测量一个角,角的大小也可以按其度数比较,度数大的角则大,度数小的则小.反之,角大度数大,角小度数小.
注意:使用量角器应注意的问题.即三点:对中、重合、读数.
如:
请用量角器量出你的一副三角尺中各个角的度数.
1、请同学们同桌两人分别画两个角,然后交换用量角器测量其度数,比较它们的大小.
量一量,比一比
2、观察下图中的∠AOC,∠COB和∠AOB ,如何表示它们的关系.
∠AOC+∠COB=∠AOB
∠AOB-∠AOC=∠COB
∠AOB-∠COB=∠AOC
1、下列说法正确的是( )
A,角的边越长,则角越大
B,角的大小与边的长短无关
C,角的大小与顶点的位置有关
D,角的大小决定于始边旋转的方向
B
2、下图一组角,其大小顺序正确的是( )
A, ∠1< ∠2< ∠3< ∠4 B, ∠1< ∠4< ∠2< ∠3
C, ∠1< ∠4< ∠3< ∠2 D, ∠1< ∠3< ∠2<∠4
D
∠
1
2
3
4
选一选:
例 如图,求解下列问题:
(1)比较∠AOC 与∠BOC,∠BOD与∠COD的大小.
(2)将∠AOC 写成两个角的和或两个角的差的形式.
O
D
A
C
解:(1)由图可以看出:
(2)∠AOC=∠AOB+∠BOC
∠AOC>∠BOC,(OB在∠AOC 内)
∠BOD>∠COD,(OC在∠BOD 内)
B
∠AOC=∠AOD-∠COD
在一张透明纸上任意画一个角∠AOB,把这张纸折叠,使角的两边OA与OB重合,然后把纸展开,画出折痕OC. ∠AOC与∠BOC之间有怎样的大小关系?
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线.
O
A
B
C
如图,射线OC是∠AOB的平分线或OC平分∠AOB
则有 ∠AOC=∠BOC= ∠AOB, 或 ∠AOB=2∠AOC=2∠BOC.
合作学习
观察下图,∠ 1+ ∠ 2与Rt∠ AOB相等吗?你是怎么判断的呢?
1
2
1
2
1
A
O B
如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余.也可以说其中一个角是另一个角的余角.
如果∠1+∠2=90°,那么∠1与∠2互为余角,∠1是∠2的余角,∠2是∠1的余角.
再观察下图, ∠ 3+ ∠ 4与∠ AOB相等吗?你是怎么判断的呢?
如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角.
如上图, ∠3与∠4互为补角,∠3是∠4的补角,∠4也是∠3的补角.
互补的数量关系: ∠α+∠β=180 °
数量关系:∠3+∠4=180 °.
3
4
3
O
4
A
B
3
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等。
同角或等角的补角相等。
1
2
1
2
做一做
解 因为 ∠1+∠3=42°+48°=90°,
所以 ∠1与∠3互余.
因为 ∠1+∠2=42°+138°=180°,
所以 ∠1与∠2互补.
如图,已知∠1=42°,∠2=138°,
∠3=48°,问图中有没有互余或互补的角?
若有,请把它们写出来,并说明理由.
1
2
3
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
