安徽省合肥瑶海三十八中2021-2022学年九上段考(12月)数学试卷(Word版,含简单答案)
文档属性
| 名称 | 安徽省合肥瑶海三十八中2021-2022学年九上段考(12月)数学试卷(Word版,含简单答案) |  | |
| 格式 | zip | ||
| 文件大小 | 274.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 21:36:58 | ||
图片预览


文档简介
合肥瑶海三十八中2021-2022学年九上段考(12月)数学试卷(含答案)
温馨提示:本试卷内容沪科版九上全册第21章~23章、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若3m=4n(mn≠0),则下列比例式成立的是( )
A. B. C. D.
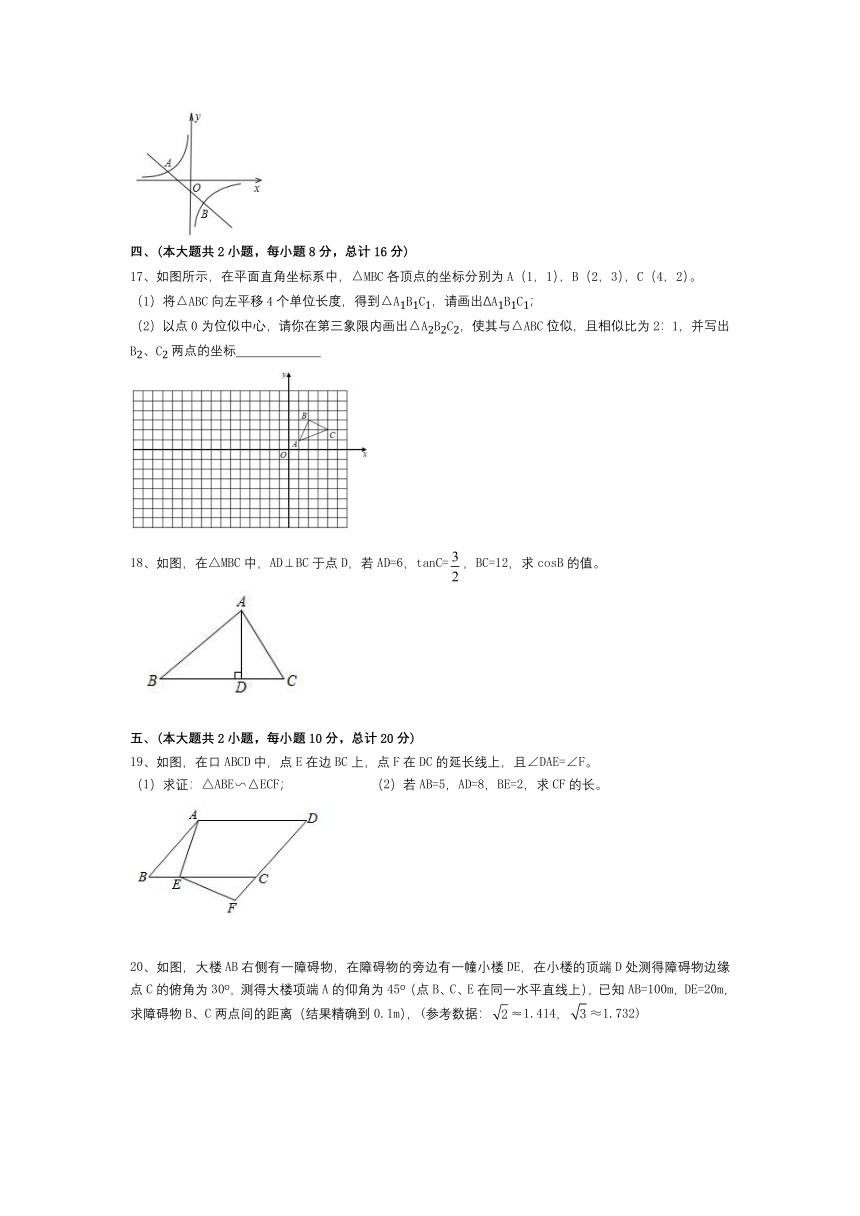
2.如图,以下四个条件中不能判定△ABC∽△ACD的是( )
A.∠B=∠ACD B.∠ACB=∠ADC C. AB CD=AC BC D. AC2=AD AB
第2题图 第5题图 第7题图 第8题图 第9题图
3.在Rt△ABC中,∠C=90 , sinA=, 则tanA=( )
A. B. C. D.
4.在平面直角坐标系中,将抛物线y=x2-2x-1先向下平移1个单位长度,再向左平移2个单位长度,所得抛物线的表达式为( )
A. y=(x+1)2-3 B. y=(x+1)2-1 C. y=(x-3)2-1 D. y=(x-3)2-3
5.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,CE平分∠ACB交BD于点E,若AD=,
则BE=( )
A.4 B. C. D.
6. 已知锐角a满足tan(α+10°)=1, 则锐用α的度数为( )
A. 20° B.35 C.45 D.50°
7. 如图,已知△ABC和△ADE均是等边三角形,点D在边BC上,DE与AC相交于点F,若AB=6,AD=5,CD=4,则EF=( )
A. B. C. D.
8、如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=10m,且tan∠CEF=,那么矩形ABCD的面积为 cm;
A 280 B 300 C 320 D 360
9、如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,AE是BC边上的中线,过点B作BD⊥AE于点O,交AC于点D,则AD的长为( )
A. 2 B C D
10、已知关于x的物线y=x-ax-4的对称轴为直线x=2,则下列各点在这条物线上的是( )
A (3,4) B (-2,-8) C (4,4) D (,)
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知∠A为锐角,若cosA=sin65°,则∠A的度数为
12、如图,在边长为1的正方形网格中,A、B、C、D、E各点均为格点,则图中能用字母表示的各三角形
∽ΔABC。
13、在平面直角坐标系中,抛物线y=x2-6x+2的对称轴交x轴于点A,点B是位于x物上方的对称轴上一点,BC//x
轴交对称轴右侧的抛物线于点C,若四边形AOBC是平行四边形,侧点C到x轴的距离为
14、如图,ΔABC是边长为6的等边三角形,CE平分外角∠ACF,点D在AC上,连接BD并延长长交CE于点E,
若CD=AD,则 ;BE=
三、(本大题共2小题,每小题8分,总计16分)
15、计算:
16、如图,一次函数y= kx+b与反比例函数y=的图象交于A(-2,1)、B(1,a)两点.
(1)分别求出反比例函数与一次函数的关系式;
(2)观察图象,直接写出当反比例函数值大于一次函数值时x的取值范围;
四、(本大题共2小题,每小题8分,总计16分)
17、如图所示,在平面直角坐标系中,△MBC各顶点的坐标分别为A(1,1),B(2,3),C(4,2)。
(1)将△ABC向左平移4个单位长度,得到△A1B1C1,请画出ΔA1B1C1;
(2)以点0为位似中心,请你在第三象限内画出△A2B2C2,使其与△ABC位似,且相似比为2:1,并写出B2、C2两点的坐标
18、如图,在△MBC中,AD⊥BC于点D,若AD=6,tanC=,BC=12,求cosB的值。
五、(本大题共2小题,每小题10分,总计20分)
19、如图,在口ABCD中,点E在边BC上,点F在DC的延长线上,且∠DAE=∠F。
(1)求证:△ABE∽△ECF; (2)若AB=5,AD=8,BE=2,求CF的长。
20、如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30 ,测得大楼项端A的仰角为45 (点B、C、E在同一水平直线上),已知AB=100m,DE=20m,求障碍物B、C两点间的距离(结果精确到0.1m),(参考数据:≈1.414,≈1.732)
六、(本大题共1小题,每小题12分,总计12分)
21、如图,在△ABC中,AB=AC,∠A为锐角且不等于60 ,AD平分∠BAC交BC于点D,BE⊥AC于点E,AD交BE于
点F.
(1)写出图中所有与△ACD相似的三角形(全等除外); (2)连接DE,求证:△ABF∽△EDF;
七、(本大题共1小题,每小题12分,总计12分)
22、在如图所示的平面直角坐标系中,抛物线y=ax2+bx-2交x轴于A、B两点。交y轴于点C,且0A=20C=8OB,
点P是第三象限内抛物线上的一动点。
(1)求此抛物线的函数表达式;
(2)若PC∥AB,求点P的坐标;
(3)连接AC,求△PAC面积的最大值及此时点P的坐标。
八、(本大题共1小题,每小题14分,总计14分)
23、在△ABC中,P为AB边上一点
(1)如图1,若∠ACP=∠B,求证: AC2=AP AB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP ,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A= ∠BMP=60 ,直接写出 BP的长.
合肥瑶海三十八中2021-2022学年九上段考(12月)数学试卷答案
1 2 3 4 5 6 7 8 9 10
B C D A B B A C B D
11、 25°; 12、 ΔDBE; 13、 2; 14、 (1) ; (2)3;
15、 0
16、(1); y=-x-1; (2)-2<x<0或x>1;
17、(1)如图所示:(2)B2(-4,-6);C2(-8,-4)
18、
(2);
20、约45.4米;
21、(1)ΔAFD; ΔBCE;ΔBFD;
22、(1)y=x2+x-2; (2)P(-,-2); (3)P(-2,-5)
23、
(2)①PB=; ②PB=-1
温馨提示:本试卷内容沪科版九上全册第21章~23章、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若3m=4n(mn≠0),则下列比例式成立的是( )
A. B. C. D.
2.如图,以下四个条件中不能判定△ABC∽△ACD的是( )
A.∠B=∠ACD B.∠ACB=∠ADC C. AB CD=AC BC D. AC2=AD AB
第2题图 第5题图 第7题图 第8题图 第9题图
3.在Rt△ABC中,∠C=90 , sinA=, 则tanA=( )
A. B. C. D.
4.在平面直角坐标系中,将抛物线y=x2-2x-1先向下平移1个单位长度,再向左平移2个单位长度,所得抛物线的表达式为( )
A. y=(x+1)2-3 B. y=(x+1)2-1 C. y=(x-3)2-1 D. y=(x-3)2-3
5.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,CE平分∠ACB交BD于点E,若AD=,
则BE=( )
A.4 B. C. D.
6. 已知锐角a满足tan(α+10°)=1, 则锐用α的度数为( )
A. 20° B.35 C.45 D.50°
7. 如图,已知△ABC和△ADE均是等边三角形,点D在边BC上,DE与AC相交于点F,若AB=6,AD=5,CD=4,则EF=( )
A. B. C. D.
8、如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=10m,且tan∠CEF=,那么矩形ABCD的面积为 cm;
A 280 B 300 C 320 D 360
9、如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,AE是BC边上的中线,过点B作BD⊥AE于点O,交AC于点D,则AD的长为( )
A. 2 B C D
10、已知关于x的物线y=x-ax-4的对称轴为直线x=2,则下列各点在这条物线上的是( )
A (3,4) B (-2,-8) C (4,4) D (,)
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知∠A为锐角,若cosA=sin65°,则∠A的度数为
12、如图,在边长为1的正方形网格中,A、B、C、D、E各点均为格点,则图中能用字母表示的各三角形
∽ΔABC。
13、在平面直角坐标系中,抛物线y=x2-6x+2的对称轴交x轴于点A,点B是位于x物上方的对称轴上一点,BC//x
轴交对称轴右侧的抛物线于点C,若四边形AOBC是平行四边形,侧点C到x轴的距离为
14、如图,ΔABC是边长为6的等边三角形,CE平分外角∠ACF,点D在AC上,连接BD并延长长交CE于点E,
若CD=AD,则 ;BE=
三、(本大题共2小题,每小题8分,总计16分)
15、计算:
16、如图,一次函数y= kx+b与反比例函数y=的图象交于A(-2,1)、B(1,a)两点.
(1)分别求出反比例函数与一次函数的关系式;
(2)观察图象,直接写出当反比例函数值大于一次函数值时x的取值范围;
四、(本大题共2小题,每小题8分,总计16分)
17、如图所示,在平面直角坐标系中,△MBC各顶点的坐标分别为A(1,1),B(2,3),C(4,2)。
(1)将△ABC向左平移4个单位长度,得到△A1B1C1,请画出ΔA1B1C1;
(2)以点0为位似中心,请你在第三象限内画出△A2B2C2,使其与△ABC位似,且相似比为2:1,并写出B2、C2两点的坐标
18、如图,在△MBC中,AD⊥BC于点D,若AD=6,tanC=,BC=12,求cosB的值。
五、(本大题共2小题,每小题10分,总计20分)
19、如图,在口ABCD中,点E在边BC上,点F在DC的延长线上,且∠DAE=∠F。
(1)求证:△ABE∽△ECF; (2)若AB=5,AD=8,BE=2,求CF的长。
20、如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30 ,测得大楼项端A的仰角为45 (点B、C、E在同一水平直线上),已知AB=100m,DE=20m,求障碍物B、C两点间的距离(结果精确到0.1m),(参考数据:≈1.414,≈1.732)
六、(本大题共1小题,每小题12分,总计12分)
21、如图,在△ABC中,AB=AC,∠A为锐角且不等于60 ,AD平分∠BAC交BC于点D,BE⊥AC于点E,AD交BE于
点F.
(1)写出图中所有与△ACD相似的三角形(全等除外); (2)连接DE,求证:△ABF∽△EDF;
七、(本大题共1小题,每小题12分,总计12分)
22、在如图所示的平面直角坐标系中,抛物线y=ax2+bx-2交x轴于A、B两点。交y轴于点C,且0A=20C=8OB,
点P是第三象限内抛物线上的一动点。
(1)求此抛物线的函数表达式;
(2)若PC∥AB,求点P的坐标;
(3)连接AC,求△PAC面积的最大值及此时点P的坐标。
八、(本大题共1小题,每小题14分,总计14分)
23、在△ABC中,P为AB边上一点
(1)如图1,若∠ACP=∠B,求证: AC2=AP AB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP ,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A= ∠BMP=60 ,直接写出 BP的长.
合肥瑶海三十八中2021-2022学年九上段考(12月)数学试卷答案
1 2 3 4 5 6 7 8 9 10
B C D A B B A C B D
11、 25°; 12、 ΔDBE; 13、 2; 14、 (1) ; (2)3;
15、 0
16、(1); y=-x-1; (2)-2<x<0或x>1;
17、(1)如图所示:(2)B2(-4,-6);C2(-8,-4)
18、
(2);
20、约45.4米;
21、(1)ΔAFD; ΔBCE;ΔBFD;
22、(1)y=x2+x-2; (2)P(-,-2); (3)P(-2,-5)
23、
(2)①PB=; ②PB=-1
同课章节目录
