2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用 同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用 同步练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 842.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 19:27:25 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》同步练习题(附答案)
1.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则∠APD的余弦值为( )
A. B. C. D.
2.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积=(弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )
A. B. C. D.
3.如图所示,在Rt△BAD中,延长斜边BD到点C,使DC=BD,连接AC,若tanB=,则tan∠CAD的值为( )
A. B. C. D.
4.如图,在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,DE⊥AC于点E,连接BE,则tan∠CBE的值等于( )
A. B. C. D.
5.如图,在边长为1的小正方形网格中,点A、B、C均在格点上,则tanB的值为 .
6.如图,在Rt△ABC中,∠ACB=90°,AC=2,tanB=,CD平分∠ACB交AB于点D,DE⊥BC,垂足为点E,则DE= .
7.安徽滁州琅琊山会峰阁更名为琅琊阁,如图①是悬挂着巨大匾额的琅琊阁,如图②,线段BC是悬挂在墙壁AM上的匾额的截面示意图.已知BC=2米,∠MBC=34°,从水平地面点D处看点C,仰角∠ADC=45°,从点E处看点B,仰角∠AEB=56°,且DE=4.4米,求匾额悬挂的高度AB的长.(结果精确到0.1米,参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
8.如图是某款手机支架摆放手机时的侧面示意图,现测得支撑板AC=10cm,CE=7cm,∠ACE=65°,∠CAB=60°,求手机底端E到底座AB的距离,(精确到0.1,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,≈1.73)
9.一辆汽车在A处测得东北方向(北偏东45°)有一古建筑C,汽车向正东方向以每小时40公里的速度行驶1小时到达B处时,又观测到古建筑C在北偏东16°方向上,求此时汽车与古建筑相距多少公里?(sin45°=0.71,sin61°≈0.87,cos61°≈0.48,tan61°≈1.80)
10.如图,一艘船由A港沿北偏东70°方向航行60海里到达B港,然后再沿北偏西35°方向航行至C港,C港在A港北偏东25°方向,求A、C两港之间的距离为多少海里(结果保留根号).
11.如图,某数学兴趣小组要测量某购物广场大楼上安装的显示屏的高度,在点A处测得大楼上显示屏的顶端C点的仰角∠BAC为45°,底端D点的仰角∠BAD为30°,沿水平地面向前走20米到达E处,测得顶端C的仰角∠BEC为71.6°,点C,D,B在同一条竖直线上,求显示屏的高度CD约为多少米?(结果精确到1米)
(参考数据:sin71.6°≈0.95,cos71.6°≈0.36,tan71.6°≈3.00,≈1.41,≈1.73)
12.中国古代人在公元前2世纪就制成了世界上最早的潜望镜,西汉初年成书的《淮南万毕术》中有这样的记载:“取大镜高悬,悬水盆于其下,则见四邻矣.”如图1所示.其工作原理主要利用光的反射原理,在图2中,A、B、C共线,OB⊥AC于点B,入射角∠COD=30°,∠OAE=15°(入射角等于反射角),AC=12米,求OB的高度.(参考数据:)
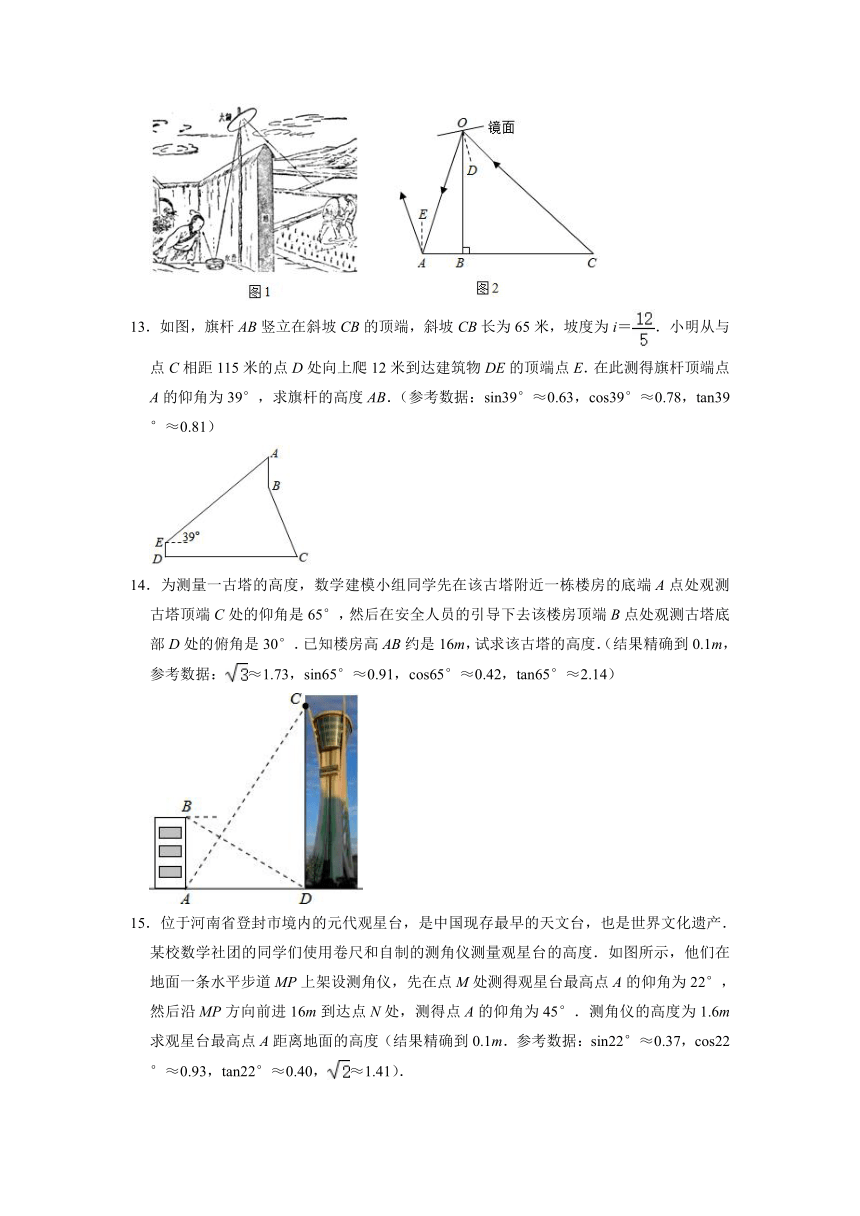
13.如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=.小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E.在此测得旗杆顶端点A的仰角为39°,求旗杆的高度AB.(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
14.为测量一古塔的高度,数学建模小组同学先在该古塔附近一栋楼房的底端A点处观测古塔顶端C处的仰角是65°,然后在安全人员的引导下去该楼房顶端B点处观测古塔底部D处的俯角是30°.已知楼房高AB约是16m,试求该古塔的高度.(结果精确到0.1m,参考数据:≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
15.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41).
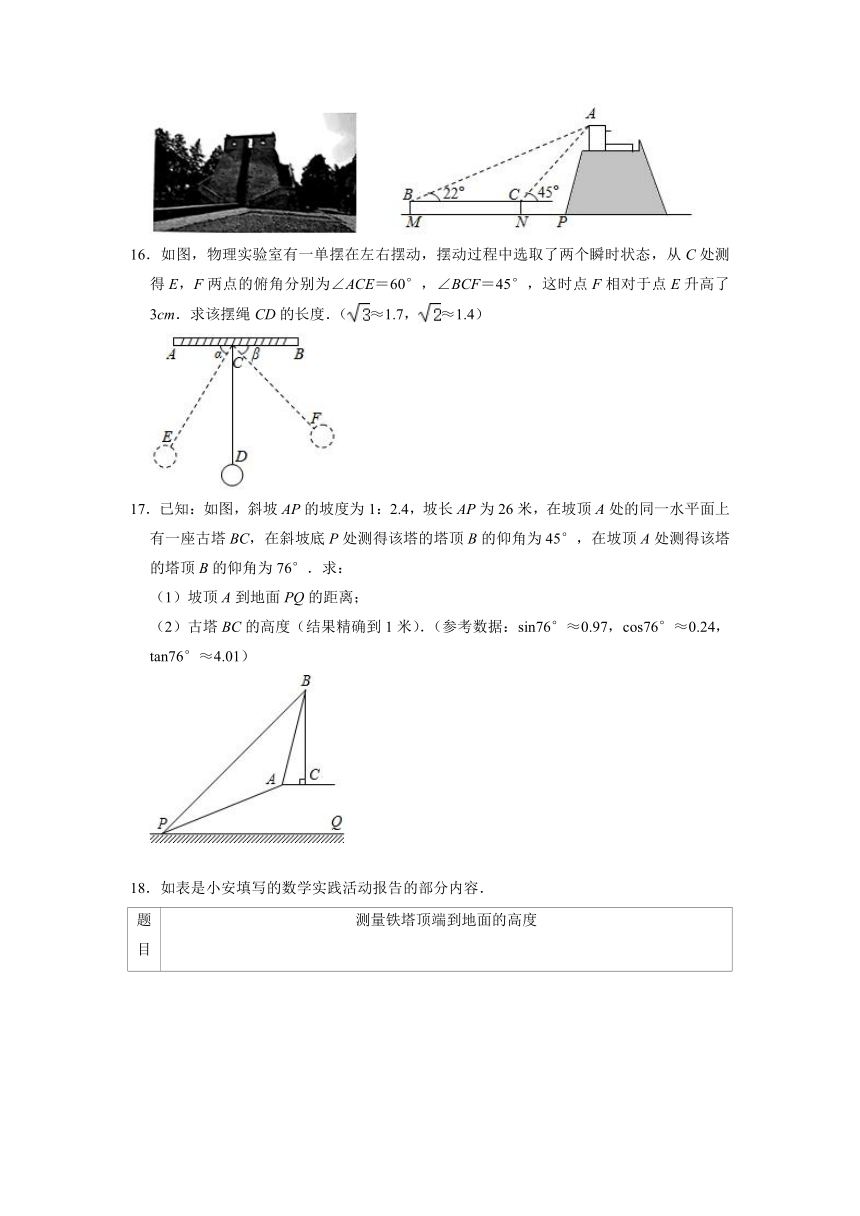
16.如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E,F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了3cm.求该摆绳CD的长度.(≈1.7,≈1.4)
17.已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
18.如表是小安填写的数学实践活动报告的部分内容.
题目 测量铁塔顶端到地面的高度
测量目标示意图
相关数据 CD=20m,α=45°,β=52°
求铁塔的高度FE.(结果精确到1米)
【参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.28】
19.如图1是一款可调节儿童书桌椅,图2是它的示意图,座位DE宽度为40cm,其竖直高度CD为30cm,O为桌面板AB的中点,某儿童坐在座位上眼睛F距离水平地面的高度为100cm.研究表明:当桌面板与竖直方向夹角∠AOC=80°,视线FO与桌面板所成锐角∠FOA=30°时最舒适,问此时OD高度应调节为多少?(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,结果精确到1cm)
20.已知:如图,在△ABC中,AD⊥BC于点D,E是AD的中点,连接CE并延长交边AB于点F,AC=13,BC=8,cos∠ACB=.
(1)求tan∠DCE的值;
(2)求的值.
21.为积极宣传国家相关政策,某村在一山坡的顶端的平地上竖立一块宣传牌AB.小明为测得宣传牌的高度,他站在山脚C处测得宣传牌的顶端A的仰角为40°,已知山坡CD的坡度i=1:2,山坡CD的长度为4米,山坡顶端D与宣传牌底端B的水平距离为2米,求宣传牌的高度AB(精确到1米)
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,≈2.24)
22.如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cosA的值;
(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.
23.《奔跑吧》节目组,设计了一款新游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向,且BD=BC=30m.求从A地跑到D地的路程.
24.“低碳环保,你我同行”.近两年,南京市区的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
25.如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成60°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.
26.如图,三条平行的高速公路l1、l2、l3分别经过A、B、C三个城市,AB、AC分别为两条连接城市的普通公路,AB、AC分别与l1成30°、45°角,已知AB=200千米,AC=400千米,求两条高速公路l2、l3之间的距离(结果保留根号).
27.某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上探测点A、B相距4m,探测线与地面的夹角分别是30°和60°,试确定生命所在点C的深度(结果精确到0.1m,参考数据:≈1.414,≈1.732)
参考答案
1.解:取格点E,连接AE、BE,如图:
设网格中的小正方形的边长为1,
则BE=,
AE=,
AB=.
∵BE2+AE2=2+8=10,
AB2=10,
∴BE2+AE2=AB2.
∴∠AEB=90°.
由题意:∠EBD=∠CDB=45°.
∵∠APD=∠CDB+∠PBD=45°+∠PBD,
∠ABE=∠DBE+∠PBD=45+∠PBD,
∴∠APD=∠ABE.
在Rt△ABE中,cos∠ABE=.
∴cos∠APD=.
故选:C.
2.解:如图,作OH⊥AB于H.
由题意:AB=8,OA﹣OH=3,
∵OH⊥AB,
∴AH=BH=4,
∵AH2+OH2=OA2,
∴42=(OA+OH)(OA﹣OH),
∴OA+OH=,
∴OA=,OH=,
∴cos∠OAB===,
故选:B.
3.解:如图,作DE∥AC交AB于E.
在Rt△ABD中,∵tanB==
∴可以假设AD=5k,AB=3k,
∴BD=k,CD=k,
∵DE∥AC,
∴∠DAC=∠ADE,==,
∴BE=2k,
∴AE=k,
∴tan∠CAD=tan∠ADE===,
故选:D.
4.解:设AB=4a,
∵在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,
∴BC=2a,AC=2a,AD:AB=1:4,
∵∠C=90°,DE⊥AC,
∴∠AED=90°,
∴∠AED=∠C,
∴DE∥BC,
∴△AED∽△ACB,
∴,
∴,
∴AE=,
∴EC=AC﹣AE=,
∴tan∠CBE=,
故选:C.
5.解:如图,取格点E,连接AE,EC,则B,A,E共线,∠E=90°.
∵EC==,BE==2,
∴tanB==.
故答案为:.
6.解:在Rt△ABC中,AC=2,tanB=,
∴BC==,
如图,过点D作DF⊥AC,垂足为F,
∵CD平分∠ACB,DE⊥BC,
∴DE=DF,
由三角形的面积公式得,
AC DF+BC DE=AC BC,
即:2DE+DE=2×,
解得,DE=,
7.解:过点C作CN⊥AB,CF⊥AD,垂足为N、F,如图所示:
在Rt△BCN中,
CN=BC sin∠MBC=2×0.56=1.12(米),
BN=BC×cos34°=2×0.83=1.66(米),
在Rt△ABE中,
AE=AB tan∠EBA=AB×tan34°=0.67AB,
∵∠ADC=45°,
∴CF=DF,
∴BN+AB=AD﹣AF=AD﹣CN,
即:1.66+AB=0.67AB+4.4﹣1.12,
解得,AB≈4.9(米).
答:匾额悬挂的高度AB的长约为4.9米.
8.解:过点C作CF⊥AB于点F,过点E作EG⊥CF于G,过点E作EH⊥AB于H,则,
在Rt△ACF中,∠A=60°,AC=10cm,∠ACF=30°,
∵sin,
∴CF=AC sin60°=10×=5≈8.65cm,
在Rt△CGE中,∠GCE=65°﹣30°=35°,CE=7cm,
∵cos,
∴CG=7×cos∠GCE=7×cos35°=7×0.82=5.74cm,
∴EH=GF=CF﹣CG=8.65﹣5.74=2.9(cm),
答:手机底端E到底座AB的距离大约为2.9cm.
9.解:过B作BD⊥AC,垂足为D,过B作BE⊥AB,交AC于E.
Rt△ABD中,∠DAB=45°,AB=40×1=40(公里),
∴BD=ABsin45°=40×=20(公里),
Rt△CBD中,∠CBD=∠CBE+∠EBD=45°+16°=61°,
∴BC=≈=(公里),
答:此时汽车与古建筑相距公里.
10.解:作BD⊥AC于点D,如右图所示,
由已知可得,
∠1=25°,∠2=70°,∠3=35°,AB=60海里,
∵m∥n,
∴∠2=∠4=70°,
∴∠CBA=180°﹣∠3﹣∠4=180°﹣35°﹣70°=75°,
∵∠1=25°,∠2=70°,
∴∠CAB=45°,
∵BD⊥AC,AB=60海里,
∴∠DAB=∠DBA=45°,
∴AD=BD=60海里,∠CBD=30°,
∴CD=BD tan∠CBD=60×=20(海里),
∴AC=AD+CD=(60+20)(海里),
答:A、C两港之间的距离为(60+20)海里.
11.解:由已知可得,
∠BAC=45°,∠BAD=30°,∠CEB=71.6°,AE=20米,
∵BE=,AB=,AE=AB﹣BE,
∴20≈﹣,
解得BC=30米,
∴AB=30米,
∴BD=AB tan30°=30×,
∴CD=BC﹣BD=30﹣30×≈13(米),
即显示屏的高度CD约为13米.
12.解:∵∠COD=30°,(入射角等于反射角),
∴∠AOD=30°,
∴∠AOC=60°,
∵AE⊥AB,OB⊥AB,∠OAE=15°,
∴AE∥BO,∠OBA=∠OBC=90°,
∴∠OAE=∠AOB=15°,
∴∠BOC=∠AOC﹣∠AOB=45°,
∴∠C=∠BOC,
∴OB=BC,
作AF⊥OC交OC于点F,
∵AC=12,∠C=45°,
∴AF=6,
∵∠AFO=90°,∠AOF=60°,
∴AO===4,
设BC=x,则AB=12﹣x,OB=x,
∵∠OBA=90°,
∴AB2+OB2=OA2,
∴(12﹣x)2+x2=(4)2,
解得x1=6+2,x2=6﹣2,
∵OB>AB,
∴6﹣2不合题意,
∴OB=6+2≈6+2×1.7=9.4(米),
即OB的高度是9.4米.
13.解:过点B作BF⊥CD,垂足为F,过点E作EG⊥BF,垂足为G,
在Rt△BCF中,
由斜坡BC的坡度i=,
得,=,
∵BC=65米,
设BF=12x(米),FC=5x(米),
由勾股定理得,(12x)2+(5x)2=652,
∴x=5,
∴BF=60米,FC=25米,
∵DC=115米,
∴DF=DC﹣FC=115﹣25=90(米)=EG,
在Rt△AEG中,AG=EG tan39°≈90×0.81=72.9(米),
∴AB=AG+FG﹣BF=72.9+12﹣60=24.9(米),
答:旗杆的高度AB为24.9米.
14.解:∵顶端B点处观测古塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,AB=16m,tan30°==,
∴AD=AB=16(m),
∵在一楼房的底端A点处观测古塔顶端C处的仰角是65°,
在Rt△ACD中,tan∠CAD=,
∴CD=AD tan65°≈16×2.14≈59.2(m).
答:该古塔的高度约为59.2米.
15.解:过A作AD⊥PM于D,延长BC交AD于E,
则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16m,DE=CN=BM=1.6m,
∵∠AEC=90°,∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=AE,
设AE=CE=x,
∴BE=16+x,
∵∠ABE=22°,
∴tan22°==≈0.40,
解得:x≈10.7(m),
∴AD≈10.7+1.6=12.3(m),
答:观星台最高点A距离地面的高度约为12.3m.
16.解:分别过点E、F作EG⊥CD,FH⊥CD,垂足分别为G、H,
设摆绳CD的长度为xcm.则CE=CF=xcm.
由题意知:HG=3,∠CEG=60°,∠CFH=45°.
在Rt△CEG中,sin∠CEG=,
∴CG=CE sin∠CEG=x sin60°,
在Rt△CFH中,sin∠CFH=,
∴CH=CF sin∠CFH=x sin45°.
∵HG=CG﹣CH,
∴x sin60°﹣x sin45°=3,
解得x=6(+)≈18.6.
答:摆绳CD的长度为18.6cm.
17.解:(1)过点A作AH⊥PQ,垂足为点H.
∵斜坡AP的坡度为1:2.4,∴=,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26. 解得k=2.
∴AH=10(m).
答:坡顶A到地面PQ的距离为10m.
(2)延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x﹣14.
在Rt△ABC中,tan76°=,即≈4.0,
解得x=,即x≈19,
答:古塔BC的高度约为19米.
18.解:∵在Rt△DFH中,α=45°,
∴DH=FH,
∵四边形DCEH是矩形,
∴DH=CE,
∴FH=CE,
设FE=x米,则CE=(x﹣20)米,
在Rt△EFC中,tanβ=,
即x=(x﹣20)tan52°,
解得:x≈91,
答:铁塔FE的高度约为91米.
19.解:如图2,作OH⊥FG,垂足为H,延长FE交水平线CG于点G,
则OH=40,∠FOH=20°.
在直角△FHO中,tan∠FOH=,即,tan20°=.
∴FH=tan20°×40≈0.36×40=14.4(cm).
∴OD=100﹣14.4﹣30≈56(cm).
答:此时OD的高度应调节为56cm.
20.解:(1)∵AD⊥BC,
∴∠ADC=90°,
在Rt△ADC中,AC=13,cos∠ACB==,
∴CD=5,
由勾股定理得:AD==12,
∵E是AD的中点,
∴ED=AD=6,
∴tan∠DCE==;
(2)过D作DG∥CF交AB于点G,如图所示:
∵BC=8,CD=5,
∴BD=BC﹣CD=3,
∵DG∥CF,
∴==,==1,
∴AF=FG,
设BG=3x,则AF=FG=5x,BF=FG+BG=8x
∴=.
21.解:延长AB 交CE于点E,过点D作DF⊥CE于点F,则四边形BDFE是矩形,
∴BD=EF,BE=DF.
在直角△CDF中,∵山坡CD的坡度i=1:2,
∴设DF=x米,则CF=2x米.
由勾股定理,得x2+(2x)2=(4)2.
解得x=4.则DF=4米,CF=8米.
∴CE=CF+EF=8+2=10米.
在直角△ACE中,∵tan40°=,
∴AE≈10×0.84=8.4(米).
∴AB=AE﹣BE=8.4﹣4≈4(米).
答:宣传牌的高度AB约为4米.
22.解:(1)∵P为AC的中点,AC=8,
∴CP=4,
∵∠ACB=90°,BC=6,
∴BP=2,
∵D是边AB的中点,P为AC的中点,
∴点E是△ABC的重心,
∴BE=BP=;
(2)如图1,过点B作BF∥CA交CD的延长线于点F,
∴,
∵BD=DA,
∴FD=DC,BF=AC,
∵CE=2,ED=3,则CD=5,
∴EF=8,
∴=,
∴=,
∴=,
设CP=k,则PA=3k,
∵PD⊥AB,D是边AB的中点,
∴PA=PB=3k
∴BC=2k,
∴AB=2k,
∵AC=4k,
∴cosA=;
(3)∵∠ACB=90°,D是边AB的中点,
∴CD=BD=AB,
∵PB2=2CD2,
∴BP2=2CD CD=BD AB,
∵∠PBD=∠ABP,
∴△PBD∽△ABP,
∴∠BPD=∠A,
∵∠A=∠DCA,
∴∠DPE=∠DCP,
∵∠PDE=∠CDP,
∴△DPE∽△DCP,
∴PD2=DE DC,
∵DE=3,DC=5,
∴PD=.
23.解:如图,过点D作DH垂直于AC,垂足为H,
由题意可知:
∠DAC=75°﹣30°=45°,∠DCA=180°﹣75°﹣45°=60°,
∵BC=CD,
∵△BCD是等边三角形,
∴∠DBC=60°,BD=BC=CD=30(m),
∴DH=×30=15(m),
∴AD=DH=15(m).
答:从A地到D地的距离是15m.
24.解:(1)在Rt△ADF中,由勾股定理得,
AD===15(cm;
(2)AE=AD+CD+EC=15+30+15=60(cm),
如图②,过点E作EH⊥AB于H,
在Rt△AEH中,sin∠EAH=,
则EH=AE sin∠EAH=AB sin75°≈60×0.97=58.2(cm).
答:点E到AB的距离为58.2 cm.
25.解:根据题意得:AB⊥EF,DE⊥EF,
∴∠ABC=90°,AB∥DE,
∴△ABF∽△DEF,
∴,即,
解得:AB=3.6,
∵cos∠BAC=,
∴AC==7.2米,
∴AB+AC=3.6+7.2=10.8米.
答:这棵大树没有折断前的高度为10.8米.
26.解:过A作AD⊥l2于D,延长AD交l3于E,
在RT△ABD中,∠ABD=30°,AB=200,
∴AD=100,
在RT△ACE中,∠ACE=45°,AC=400,
∵sin∠ACE=,
∴AE=AC sin45°=200,
∴DE=AE﹣DE=200﹣100,
答:两条高速公路l2、l3之间的距离为(200﹣100)千米.
27.解:由对顶角相等易得∠DAC=30°.
∴∠BCA=30°,
∴BC=AB=4.
作CD⊥AB于点D.
∴CD=BC×sin60°=2≈3.5(m).
1.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则∠APD的余弦值为( )
A. B. C. D.
2.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积=(弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )
A. B. C. D.
3.如图所示,在Rt△BAD中,延长斜边BD到点C,使DC=BD,连接AC,若tanB=,则tan∠CAD的值为( )
A. B. C. D.
4.如图,在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,DE⊥AC于点E,连接BE,则tan∠CBE的值等于( )
A. B. C. D.
5.如图,在边长为1的小正方形网格中,点A、B、C均在格点上,则tanB的值为 .
6.如图,在Rt△ABC中,∠ACB=90°,AC=2,tanB=,CD平分∠ACB交AB于点D,DE⊥BC,垂足为点E,则DE= .
7.安徽滁州琅琊山会峰阁更名为琅琊阁,如图①是悬挂着巨大匾额的琅琊阁,如图②,线段BC是悬挂在墙壁AM上的匾额的截面示意图.已知BC=2米,∠MBC=34°,从水平地面点D处看点C,仰角∠ADC=45°,从点E处看点B,仰角∠AEB=56°,且DE=4.4米,求匾额悬挂的高度AB的长.(结果精确到0.1米,参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
8.如图是某款手机支架摆放手机时的侧面示意图,现测得支撑板AC=10cm,CE=7cm,∠ACE=65°,∠CAB=60°,求手机底端E到底座AB的距离,(精确到0.1,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,≈1.73)
9.一辆汽车在A处测得东北方向(北偏东45°)有一古建筑C,汽车向正东方向以每小时40公里的速度行驶1小时到达B处时,又观测到古建筑C在北偏东16°方向上,求此时汽车与古建筑相距多少公里?(sin45°=0.71,sin61°≈0.87,cos61°≈0.48,tan61°≈1.80)
10.如图,一艘船由A港沿北偏东70°方向航行60海里到达B港,然后再沿北偏西35°方向航行至C港,C港在A港北偏东25°方向,求A、C两港之间的距离为多少海里(结果保留根号).
11.如图,某数学兴趣小组要测量某购物广场大楼上安装的显示屏的高度,在点A处测得大楼上显示屏的顶端C点的仰角∠BAC为45°,底端D点的仰角∠BAD为30°,沿水平地面向前走20米到达E处,测得顶端C的仰角∠BEC为71.6°,点C,D,B在同一条竖直线上,求显示屏的高度CD约为多少米?(结果精确到1米)
(参考数据:sin71.6°≈0.95,cos71.6°≈0.36,tan71.6°≈3.00,≈1.41,≈1.73)
12.中国古代人在公元前2世纪就制成了世界上最早的潜望镜,西汉初年成书的《淮南万毕术》中有这样的记载:“取大镜高悬,悬水盆于其下,则见四邻矣.”如图1所示.其工作原理主要利用光的反射原理,在图2中,A、B、C共线,OB⊥AC于点B,入射角∠COD=30°,∠OAE=15°(入射角等于反射角),AC=12米,求OB的高度.(参考数据:)
13.如图,旗杆AB竖立在斜坡CB的顶端,斜坡CB长为65米,坡度为i=.小明从与点C相距115米的点D处向上爬12米到达建筑物DE的顶端点E.在此测得旗杆顶端点A的仰角为39°,求旗杆的高度AB.(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
14.为测量一古塔的高度,数学建模小组同学先在该古塔附近一栋楼房的底端A点处观测古塔顶端C处的仰角是65°,然后在安全人员的引导下去该楼房顶端B点处观测古塔底部D处的俯角是30°.已知楼房高AB约是16m,试求该古塔的高度.(结果精确到0.1m,参考数据:≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
15.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41).
16.如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E,F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了3cm.求该摆绳CD的长度.(≈1.7,≈1.4)
17.已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
18.如表是小安填写的数学实践活动报告的部分内容.
题目 测量铁塔顶端到地面的高度
测量目标示意图
相关数据 CD=20m,α=45°,β=52°
求铁塔的高度FE.(结果精确到1米)
【参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.28】
19.如图1是一款可调节儿童书桌椅,图2是它的示意图,座位DE宽度为40cm,其竖直高度CD为30cm,O为桌面板AB的中点,某儿童坐在座位上眼睛F距离水平地面的高度为100cm.研究表明:当桌面板与竖直方向夹角∠AOC=80°,视线FO与桌面板所成锐角∠FOA=30°时最舒适,问此时OD高度应调节为多少?(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,结果精确到1cm)
20.已知:如图,在△ABC中,AD⊥BC于点D,E是AD的中点,连接CE并延长交边AB于点F,AC=13,BC=8,cos∠ACB=.
(1)求tan∠DCE的值;
(2)求的值.
21.为积极宣传国家相关政策,某村在一山坡的顶端的平地上竖立一块宣传牌AB.小明为测得宣传牌的高度,他站在山脚C处测得宣传牌的顶端A的仰角为40°,已知山坡CD的坡度i=1:2,山坡CD的长度为4米,山坡顶端D与宣传牌底端B的水平距离为2米,求宣传牌的高度AB(精确到1米)
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,≈2.24)
22.如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.
(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;
(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cosA的值;
(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.
23.《奔跑吧》节目组,设计了一款新游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向,且BD=BC=30m.求从A地跑到D地的路程.
24.“低碳环保,你我同行”.近两年,南京市区的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
25.如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成60°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.
26.如图,三条平行的高速公路l1、l2、l3分别经过A、B、C三个城市,AB、AC分别为两条连接城市的普通公路,AB、AC分别与l1成30°、45°角,已知AB=200千米,AC=400千米,求两条高速公路l2、l3之间的距离(结果保留根号).
27.某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上探测点A、B相距4m,探测线与地面的夹角分别是30°和60°,试确定生命所在点C的深度(结果精确到0.1m,参考数据:≈1.414,≈1.732)
参考答案
1.解:取格点E,连接AE、BE,如图:
设网格中的小正方形的边长为1,
则BE=,
AE=,
AB=.
∵BE2+AE2=2+8=10,
AB2=10,
∴BE2+AE2=AB2.
∴∠AEB=90°.
由题意:∠EBD=∠CDB=45°.
∵∠APD=∠CDB+∠PBD=45°+∠PBD,
∠ABE=∠DBE+∠PBD=45+∠PBD,
∴∠APD=∠ABE.
在Rt△ABE中,cos∠ABE=.
∴cos∠APD=.
故选:C.
2.解:如图,作OH⊥AB于H.
由题意:AB=8,OA﹣OH=3,
∵OH⊥AB,
∴AH=BH=4,
∵AH2+OH2=OA2,
∴42=(OA+OH)(OA﹣OH),
∴OA+OH=,
∴OA=,OH=,
∴cos∠OAB===,
故选:B.
3.解:如图,作DE∥AC交AB于E.
在Rt△ABD中,∵tanB==
∴可以假设AD=5k,AB=3k,
∴BD=k,CD=k,
∵DE∥AC,
∴∠DAC=∠ADE,==,
∴BE=2k,
∴AE=k,
∴tan∠CAD=tan∠ADE===,
故选:D.
4.解:设AB=4a,
∵在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,
∴BC=2a,AC=2a,AD:AB=1:4,
∵∠C=90°,DE⊥AC,
∴∠AED=90°,
∴∠AED=∠C,
∴DE∥BC,
∴△AED∽△ACB,
∴,
∴,
∴AE=,
∴EC=AC﹣AE=,
∴tan∠CBE=,
故选:C.
5.解:如图,取格点E,连接AE,EC,则B,A,E共线,∠E=90°.
∵EC==,BE==2,
∴tanB==.
故答案为:.
6.解:在Rt△ABC中,AC=2,tanB=,
∴BC==,
如图,过点D作DF⊥AC,垂足为F,
∵CD平分∠ACB,DE⊥BC,
∴DE=DF,
由三角形的面积公式得,
AC DF+BC DE=AC BC,
即:2DE+DE=2×,
解得,DE=,
7.解:过点C作CN⊥AB,CF⊥AD,垂足为N、F,如图所示:
在Rt△BCN中,
CN=BC sin∠MBC=2×0.56=1.12(米),
BN=BC×cos34°=2×0.83=1.66(米),
在Rt△ABE中,
AE=AB tan∠EBA=AB×tan34°=0.67AB,
∵∠ADC=45°,
∴CF=DF,
∴BN+AB=AD﹣AF=AD﹣CN,
即:1.66+AB=0.67AB+4.4﹣1.12,
解得,AB≈4.9(米).
答:匾额悬挂的高度AB的长约为4.9米.
8.解:过点C作CF⊥AB于点F,过点E作EG⊥CF于G,过点E作EH⊥AB于H,则,
在Rt△ACF中,∠A=60°,AC=10cm,∠ACF=30°,
∵sin,
∴CF=AC sin60°=10×=5≈8.65cm,
在Rt△CGE中,∠GCE=65°﹣30°=35°,CE=7cm,
∵cos,
∴CG=7×cos∠GCE=7×cos35°=7×0.82=5.74cm,
∴EH=GF=CF﹣CG=8.65﹣5.74=2.9(cm),
答:手机底端E到底座AB的距离大约为2.9cm.
9.解:过B作BD⊥AC,垂足为D,过B作BE⊥AB,交AC于E.
Rt△ABD中,∠DAB=45°,AB=40×1=40(公里),
∴BD=ABsin45°=40×=20(公里),
Rt△CBD中,∠CBD=∠CBE+∠EBD=45°+16°=61°,
∴BC=≈=(公里),
答:此时汽车与古建筑相距公里.
10.解:作BD⊥AC于点D,如右图所示,
由已知可得,
∠1=25°,∠2=70°,∠3=35°,AB=60海里,
∵m∥n,
∴∠2=∠4=70°,
∴∠CBA=180°﹣∠3﹣∠4=180°﹣35°﹣70°=75°,
∵∠1=25°,∠2=70°,
∴∠CAB=45°,
∵BD⊥AC,AB=60海里,
∴∠DAB=∠DBA=45°,
∴AD=BD=60海里,∠CBD=30°,
∴CD=BD tan∠CBD=60×=20(海里),
∴AC=AD+CD=(60+20)(海里),
答:A、C两港之间的距离为(60+20)海里.
11.解:由已知可得,
∠BAC=45°,∠BAD=30°,∠CEB=71.6°,AE=20米,
∵BE=,AB=,AE=AB﹣BE,
∴20≈﹣,
解得BC=30米,
∴AB=30米,
∴BD=AB tan30°=30×,
∴CD=BC﹣BD=30﹣30×≈13(米),
即显示屏的高度CD约为13米.
12.解:∵∠COD=30°,(入射角等于反射角),
∴∠AOD=30°,
∴∠AOC=60°,
∵AE⊥AB,OB⊥AB,∠OAE=15°,
∴AE∥BO,∠OBA=∠OBC=90°,
∴∠OAE=∠AOB=15°,
∴∠BOC=∠AOC﹣∠AOB=45°,
∴∠C=∠BOC,
∴OB=BC,
作AF⊥OC交OC于点F,
∵AC=12,∠C=45°,
∴AF=6,
∵∠AFO=90°,∠AOF=60°,
∴AO===4,
设BC=x,则AB=12﹣x,OB=x,
∵∠OBA=90°,
∴AB2+OB2=OA2,
∴(12﹣x)2+x2=(4)2,
解得x1=6+2,x2=6﹣2,
∵OB>AB,
∴6﹣2不合题意,
∴OB=6+2≈6+2×1.7=9.4(米),
即OB的高度是9.4米.
13.解:过点B作BF⊥CD,垂足为F,过点E作EG⊥BF,垂足为G,
在Rt△BCF中,
由斜坡BC的坡度i=,
得,=,
∵BC=65米,
设BF=12x(米),FC=5x(米),
由勾股定理得,(12x)2+(5x)2=652,
∴x=5,
∴BF=60米,FC=25米,
∵DC=115米,
∴DF=DC﹣FC=115﹣25=90(米)=EG,
在Rt△AEG中,AG=EG tan39°≈90×0.81=72.9(米),
∴AB=AG+FG﹣BF=72.9+12﹣60=24.9(米),
答:旗杆的高度AB为24.9米.
14.解:∵顶端B点处观测古塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,AB=16m,tan30°==,
∴AD=AB=16(m),
∵在一楼房的底端A点处观测古塔顶端C处的仰角是65°,
在Rt△ACD中,tan∠CAD=,
∴CD=AD tan65°≈16×2.14≈59.2(m).
答:该古塔的高度约为59.2米.
15.解:过A作AD⊥PM于D,延长BC交AD于E,
则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16m,DE=CN=BM=1.6m,
∵∠AEC=90°,∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=AE,
设AE=CE=x,
∴BE=16+x,
∵∠ABE=22°,
∴tan22°==≈0.40,
解得:x≈10.7(m),
∴AD≈10.7+1.6=12.3(m),
答:观星台最高点A距离地面的高度约为12.3m.
16.解:分别过点E、F作EG⊥CD,FH⊥CD,垂足分别为G、H,
设摆绳CD的长度为xcm.则CE=CF=xcm.
由题意知:HG=3,∠CEG=60°,∠CFH=45°.
在Rt△CEG中,sin∠CEG=,
∴CG=CE sin∠CEG=x sin60°,
在Rt△CFH中,sin∠CFH=,
∴CH=CF sin∠CFH=x sin45°.
∵HG=CG﹣CH,
∴x sin60°﹣x sin45°=3,
解得x=6(+)≈18.6.
答:摆绳CD的长度为18.6cm.
17.解:(1)过点A作AH⊥PQ,垂足为点H.
∵斜坡AP的坡度为1:2.4,∴=,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26. 解得k=2.
∴AH=10(m).
答:坡顶A到地面PQ的距离为10m.
(2)延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x﹣14.
在Rt△ABC中,tan76°=,即≈4.0,
解得x=,即x≈19,
答:古塔BC的高度约为19米.
18.解:∵在Rt△DFH中,α=45°,
∴DH=FH,
∵四边形DCEH是矩形,
∴DH=CE,
∴FH=CE,
设FE=x米,则CE=(x﹣20)米,
在Rt△EFC中,tanβ=,
即x=(x﹣20)tan52°,
解得:x≈91,
答:铁塔FE的高度约为91米.
19.解:如图2,作OH⊥FG,垂足为H,延长FE交水平线CG于点G,
则OH=40,∠FOH=20°.
在直角△FHO中,tan∠FOH=,即,tan20°=.
∴FH=tan20°×40≈0.36×40=14.4(cm).
∴OD=100﹣14.4﹣30≈56(cm).
答:此时OD的高度应调节为56cm.
20.解:(1)∵AD⊥BC,
∴∠ADC=90°,
在Rt△ADC中,AC=13,cos∠ACB==,
∴CD=5,
由勾股定理得:AD==12,
∵E是AD的中点,
∴ED=AD=6,
∴tan∠DCE==;
(2)过D作DG∥CF交AB于点G,如图所示:
∵BC=8,CD=5,
∴BD=BC﹣CD=3,
∵DG∥CF,
∴==,==1,
∴AF=FG,
设BG=3x,则AF=FG=5x,BF=FG+BG=8x
∴=.
21.解:延长AB 交CE于点E,过点D作DF⊥CE于点F,则四边形BDFE是矩形,
∴BD=EF,BE=DF.
在直角△CDF中,∵山坡CD的坡度i=1:2,
∴设DF=x米,则CF=2x米.
由勾股定理,得x2+(2x)2=(4)2.
解得x=4.则DF=4米,CF=8米.
∴CE=CF+EF=8+2=10米.
在直角△ACE中,∵tan40°=,
∴AE≈10×0.84=8.4(米).
∴AB=AE﹣BE=8.4﹣4≈4(米).
答:宣传牌的高度AB约为4米.
22.解:(1)∵P为AC的中点,AC=8,
∴CP=4,
∵∠ACB=90°,BC=6,
∴BP=2,
∵D是边AB的中点,P为AC的中点,
∴点E是△ABC的重心,
∴BE=BP=;
(2)如图1,过点B作BF∥CA交CD的延长线于点F,
∴,
∵BD=DA,
∴FD=DC,BF=AC,
∵CE=2,ED=3,则CD=5,
∴EF=8,
∴=,
∴=,
∴=,
设CP=k,则PA=3k,
∵PD⊥AB,D是边AB的中点,
∴PA=PB=3k
∴BC=2k,
∴AB=2k,
∵AC=4k,
∴cosA=;
(3)∵∠ACB=90°,D是边AB的中点,
∴CD=BD=AB,
∵PB2=2CD2,
∴BP2=2CD CD=BD AB,
∵∠PBD=∠ABP,
∴△PBD∽△ABP,
∴∠BPD=∠A,
∵∠A=∠DCA,
∴∠DPE=∠DCP,
∵∠PDE=∠CDP,
∴△DPE∽△DCP,
∴PD2=DE DC,
∵DE=3,DC=5,
∴PD=.
23.解:如图,过点D作DH垂直于AC,垂足为H,
由题意可知:
∠DAC=75°﹣30°=45°,∠DCA=180°﹣75°﹣45°=60°,
∵BC=CD,
∵△BCD是等边三角形,
∴∠DBC=60°,BD=BC=CD=30(m),
∴DH=×30=15(m),
∴AD=DH=15(m).
答:从A地到D地的距离是15m.
24.解:(1)在Rt△ADF中,由勾股定理得,
AD===15(cm;
(2)AE=AD+CD+EC=15+30+15=60(cm),
如图②,过点E作EH⊥AB于H,
在Rt△AEH中,sin∠EAH=,
则EH=AE sin∠EAH=AB sin75°≈60×0.97=58.2(cm).
答:点E到AB的距离为58.2 cm.
25.解:根据题意得:AB⊥EF,DE⊥EF,
∴∠ABC=90°,AB∥DE,
∴△ABF∽△DEF,
∴,即,
解得:AB=3.6,
∵cos∠BAC=,
∴AC==7.2米,
∴AB+AC=3.6+7.2=10.8米.
答:这棵大树没有折断前的高度为10.8米.
26.解:过A作AD⊥l2于D,延长AD交l3于E,
在RT△ABD中,∠ABD=30°,AB=200,
∴AD=100,
在RT△ACE中,∠ACE=45°,AC=400,
∵sin∠ACE=,
∴AE=AC sin45°=200,
∴DE=AE﹣DE=200﹣100,
答:两条高速公路l2、l3之间的距离为(200﹣100)千米.
27.解:由对顶角相等易得∠DAC=30°.
∴∠BCA=30°,
∴BC=AB=4.
作CD⊥AB于点D.
∴CD=BC×sin60°=2≈3.5(m).
