2021-2022学年人教版数学九年级下册28.2解直角三角形及其应用 知识点分类训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册28.2解直角三角形及其应用 知识点分类训练(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 804.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 19:27:55 | ||
图片预览


文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》
知识点分类训练(附答案)
一.解直角三角形
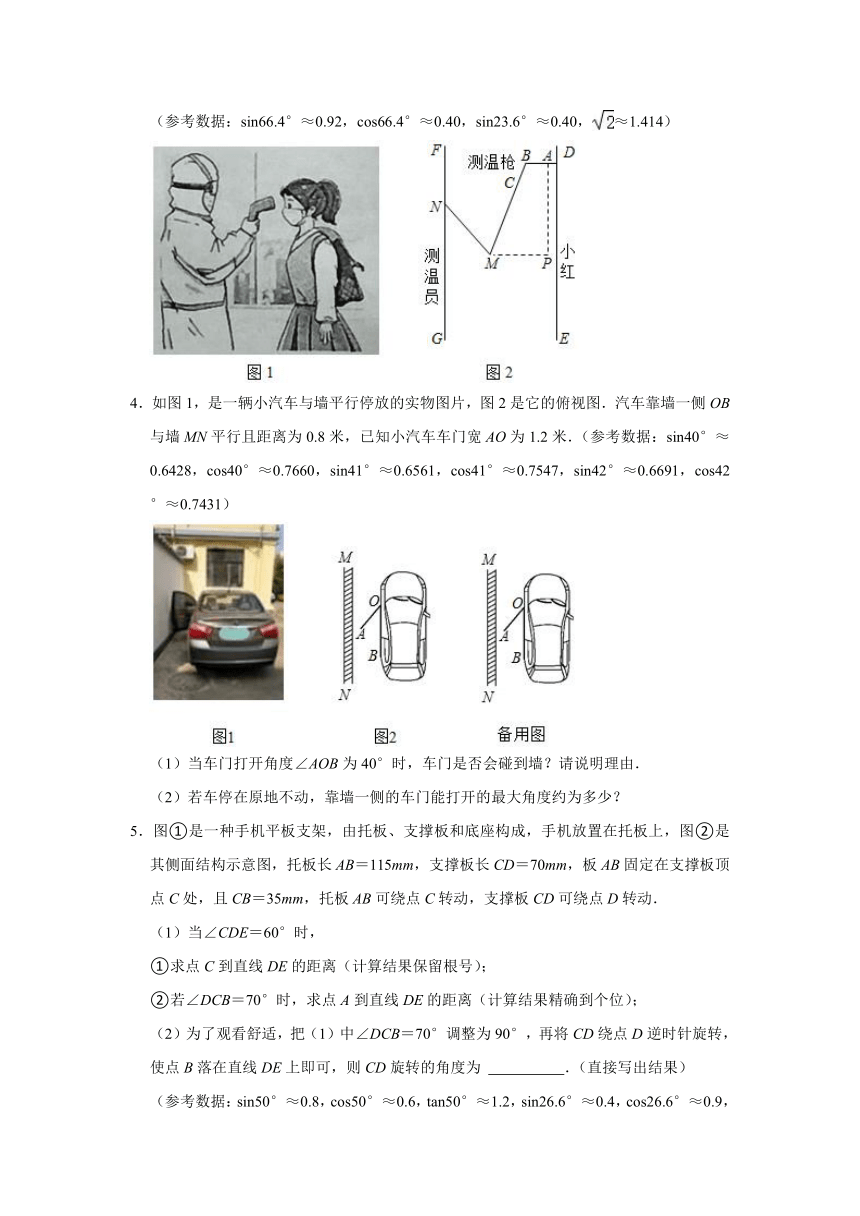
1.如图,在平面直角坐标系中,AB=3,连接AB并延长至C,连接OC,若满足OC2=BC AC,tanα=2,则点C的坐标为 .
二.解直角三角形的应用
2.图1是挂墙式淋浴花洒的实物图,图2是抽象出来的几何图形.为使身高175cm的人能方便地淋浴,应当使旋转头固定在墙上的某个位置O,花洒的最高点B与人的头顶的铅垂距离为15cm,已知龙头手柄OA长为10cm,花洒直径AB是8cm,龙头手柄与墙面的较小夹角∠COA=26°,∠OAB=146°,则安装时,旋转头的固定点O与地面的距离应为多少?(计算结果精确到1cm,参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
3.图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.
(1)求∠ABC的度数;
(2)测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
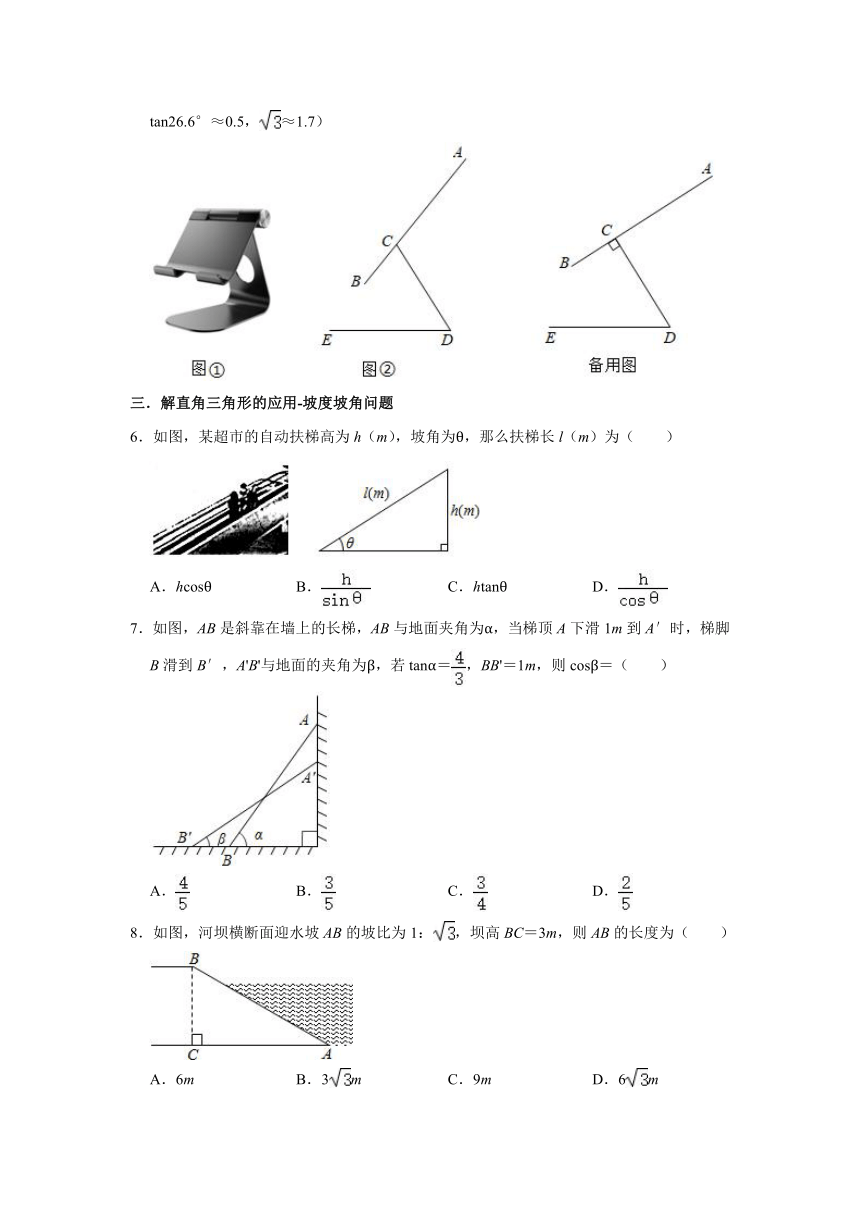
(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,≈1.414)
4.如图1,是一辆小汽车与墙平行停放的实物图片,图2是它的俯视图.汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米.(参考数据:sin40°≈0.6428,cos40°≈0.7660,sin41°≈0.6561,cos41°≈0.7547,sin42°≈0.6691,cos42°≈0.7431)
(1)当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.
(2)若车停在原地不动,靠墙一侧的车门能打开的最大角度约为多少?
5.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动.
(1)当∠CDE=60°时,
①求点C到直线DE的距离(计算结果保留根号);
②若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,则CD旋转的角度为 .(直接写出结果)
(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
三.解直角三角形的应用-坡度坡角问题
6.如图,某超市的自动扶梯高为h(m),坡角为θ,那么扶梯长l(m)为( )
A.hcosθ B. C.htanθ D.
7.如图,AB是斜靠在墙上的长梯,AB与地面夹角为α,当梯顶A下滑1m到A′时,梯脚B滑到B′,A'B'与地面的夹角为β,若tanα=,BB'=1m,则cosβ=( )
A. B. C. D.
8.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.6m B.3m C.9m D.6m
9.一架5米长的梯子斜靠在墙上,测得它与地面的夹角为40°,则梯子底端到墙角的距离为( )
A.5cos40°米 B.5sin40°米 C.米 D.米
10.如图所示,建筑物AB坐落在一斜坡的坡顶的平地上,当太阳光线与水平线夹角成60°时,测得建筑物AB在坡顶平地上的一部分影子BC=15米,在斜坡CE上的另一部分影子CD=5米,且斜坡CE的坡度为i(即tanα)=1:,求建筑物AB的高度.(结果保留根号)
四.解直角三角形的应用-仰角俯角问题
11.许昌市旅游服务中心由广场和“一门四阙”主题建筑组成,如图1.广场为迎宾广场一门”为“许昌之门”,“四闕”为广场四角的汉阙,是许昌的标志性建筑.某数学兴趣小组在迎宾广场测量旅游服务中心的高度,图2为测量示意图,MN为服务中心的对称轴,在地面的AB处架设测角仪,测得旅游服务中心的最高点D的仰角45°,利用无人机在点B的正上方57.8米处的点C处测得点D的俯角为32°,测角仪的高度AB=1.6米,FH=17.2米,DE=19.8米.
(1)求旅游服务中心的高度为多少米?(结果精确到0.1m.参考数据:sin32°≈0.530,cos32°≈0.848,tan32°≈0.625,≈1.414)
(2)兴趣小组测量后到旅游服务中心参观,发现讲解员讲解的高度为36.8m,请用物理知识解释测量值与实际值出现差距的原因,如何避免或者减小差距?
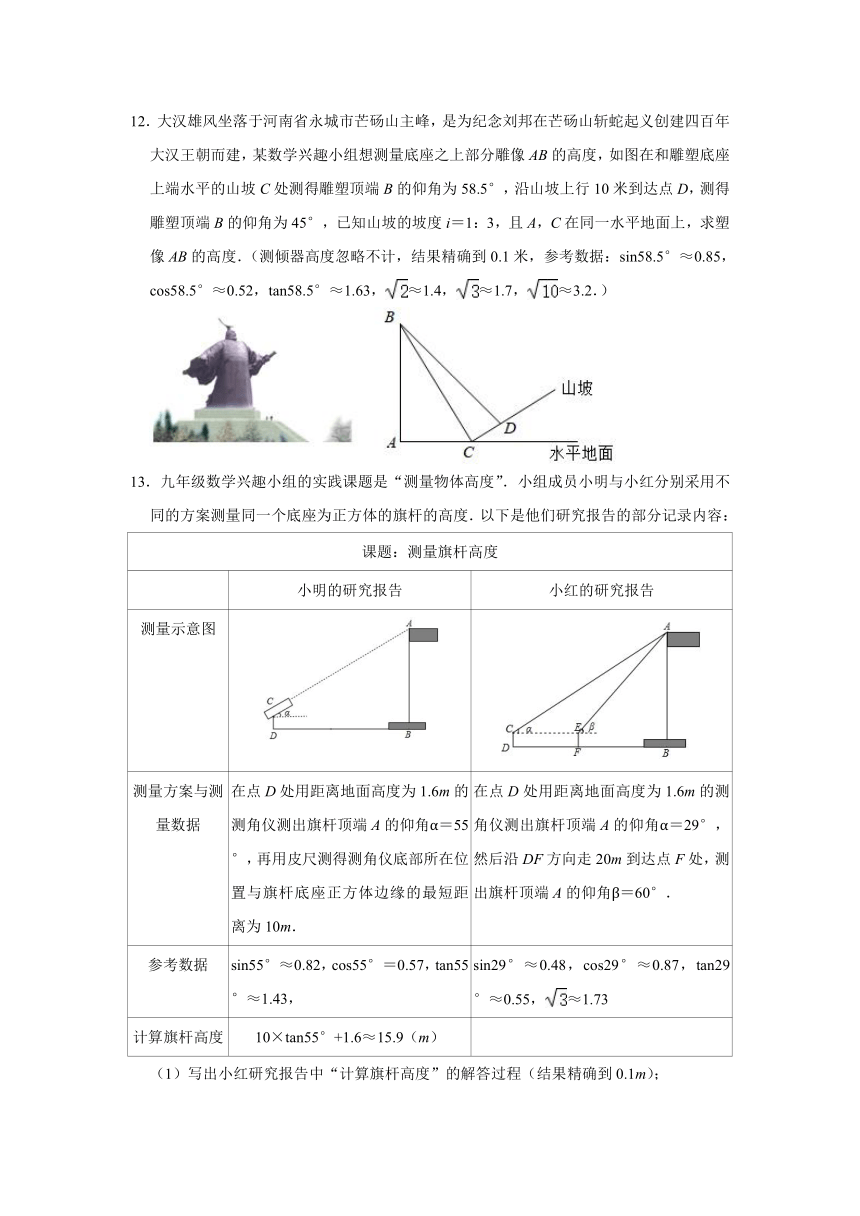
12.大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建,某数学兴趣小组想测量底座之上部分雕像AB的高度,如图在和雕塑底座上端水平的山坡C处测得雕塑顶端B的仰角为58.5°,沿山坡上行10米到达点D,测得雕塑顶端B的仰角为45°,已知山坡的坡度i=1:3,且A,C在同一水平地面上,求塑像AB的高度.(测倾器高度忽略不计,结果精确到0.1米,参考数据:sin58.5°≈0.85,cos58.5°≈0.52,tan58.5°≈1.63,≈1.4,≈1.7,≈3.2.)
13.九年级数学兴趣小组的实践课题是“测量物体高度”.小组成员小明与小红分别采用不同的方案测量同一个底座为正方体的旗杆的高度.以下是他们研究报告的部分记录内容:
课题:测量旗杆高度
小明的研究报告 小红的研究报告
测量示意图
测量方案与测量数据 在点D处用距离地面高度为1.6m的测角仪测出旗杆顶端A的仰角α=55°,再用皮尺测得测角仪底部所在位置与旗杆底座正方体边缘的最短距离为10m. 在点D处用距离地面高度为1.6m的测角仪测出旗杆顶端A的仰角α=29°,然后沿DF方向走20m到达点F处,测出旗杆顶端A的仰角β=60°.
参考数据 sin55°≈0.82,cos55°=0.57,tan55°≈1.43, sin29°≈0.48,cos29°≈0.87,tan29°≈0.55,≈1.73
计算旗杆高度 10×tan55°+1.6≈15.9(m)
(1)写出小红研究报告中“计算旗杆高度”的解答过程(结果精确到0.1m);
(2)数学老师说小明的测量结果与旗杆实际高度偏差较大,超出了误差允许范围,请你针对小明的测量方案分析测量偏差较大的原因.
14.某校一初三学生在学习了“锐角三角函数”的应用后,来到“孔子圣像”的雕像前,如图,想要用所学知识解决“孔子圣像”雕像AB的高度,他在雕像前C处用自制测角仪测得顶端A的仰角为60°,底端B的俯角为45°;又在同一水平线上的E处用自制测角仪测得顶端A的仰角为30°,已知DE=6m,求雕像AB的高度.(结果保留根号)
15.2020年6月23日,北斗卫星最后一颗全球组网卫星发射成功.运载火箭从地面A处(忽略发射塔高度)竖直向上发射,当运载火箭到达点B处时,地面D处的雷达站测得B处仰角为37°,BD=50km.10秒后,运载火箭直线上升到达点C处,此时地面E处一观测点测得C处的仰角为56°,已知点A,D,E在同一条直线上,并且D,E两处相距15km,求运载火箭从B处到C处时的平均速度(单位:km/s).
(参考数值:sin37°≈,cos37°≈,tan37°≈,sin56°≈,cos56°≈,tan56°≈)
五.解直角三角形的应用-仰角俯角问题
16.中原福塔,又名“河南广播电视塔”,是郑州市著名地标之一.小明和小亮利用卷尺和自制的测角仪测量福塔的高度.如图,小明站在点A处测得福塔顶端D的仰角为60°,小亮站在点B处测得福塔顶端D的仰角为72.3°.已知测角仪高度为1m,两人相距100m(点A,B,C在一条直线上).
(1)求中原福塔CD的高度;(结果精确到0.1m.参考数据:sin72.3≈0.95,cos72.3≈0.30,tan72.3≈3.13,)
(2)“景点简介”显示,中原福塔总高388m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
六.解直角三角形的应用-方向角问题
17.如图,一艘渔船以40海里/小时的速度由西向东追赶鱼群,在A处测得小岛C在渔船的北偏东60°方向;半小时后,渔船到达B处,此时测得小岛C在渔船的北偏东30°方向.已知以小岛C为中心,周围18海里以内为军事演习着弹危险区.如果这艘渔船继续向东追赶鱼群,是否有着弹危险?
18.如图,一艘海轮船位于灯塔P北偏东60°方向,与灯塔距离为80nmile的A处,它沿正南方向航行一段时间后,到达位于灯塔P南偏东37°方向的B处,求此时轮船所在B处与灯塔P的距离.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.7,结果取整数)
19.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习.如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是35km/h.
(1)求学校到红色文化基地A的距离?
(2)哪组同学先到达目的地?请说明理由(结果保留根号).
参考答案
一.解直角三角形
1.解:∵∠C=∠C,
∵OC2=BC AC,
即,
∴△OBC∽△OAC,
∴∠A=∠COB,
∵α+∠COB=90°,∠A+∠ABO=90°,
∴∠ABO=α,
∵tanα=2,
∴tan∠ABO=,
∴OA=2OB,
∵AB=3,
由勾股定理可得:OA2+OB2=AB2,
即,
解得:OB=3,
∴OA=6.
∴tanA=.
如图,过点C作CD⊥x轴于点D,
∵tanα=2,
∴设C(﹣m,2m),m>0,
∴AD=6+m,
∵tan∠A=,
∴,
∴,
解得:m=2,
经检验,m=2是原方程的解.
∴点C坐标为:(﹣2,4).
故答案为:(﹣2,4).
二.解直角三角形的应用
2.解:如图,过点B作地面的垂线,垂足为D,过点 A作地面GD的平行线,交OC于点E,交BD于点F,
在Rt△AOE中,∠AOE=26°,OA=10cm,
则OE=OA cos∠AOE≈10×0.90=9cm,
在Rt△ABF中,∠BAF=146°﹣90°﹣26°=30°,AB=8cm,
则BF=AB sin∠BAF=8×=4cm,
∴OG=BD﹣BF﹣OE=(175+15)﹣4﹣9=177cm,
答:旋转头的固定点O与地面的距离约为177cm.
3.解:(1)过点B作BH⊥MP,垂足为H,过点M作MI⊥FG,垂足为I,过点P作PK⊥DE,垂足为K,
∵MP=25.3cm,BA=HP=8.5cm,
∴MH=MP﹣HP=25.3﹣8.5=16.8(cm),
在Rt△BMH中,
cos∠BMH===0.4,
∴∠BMH=66.4°,
∵AB∥MP,
∴∠BMH+∠ABC=180°,
∴∠ABC=180°﹣66.4°=113.6°;
(2)∵∠BMN=68.6°,∠BMH=66.4°,
∴∠NMI=180°﹣∠BMN﹣∠BMH=180°﹣68.6°﹣66.4°=45°,
∵MN=28cm,
∴cos45°==,
∴MI≈19.80cm,
∵KI=50cm,
∴PK=KI﹣MI﹣MP=50﹣19.80﹣25.3=4.90≈4.9(cm),
∴此时枪身端点A与小红额头的距离是在规定范围内.
4.解:(1)过点A作AC⊥OB,垂足为点C,
在Rt△ACO中,
∵∠AOC=40°,AO=1.2米,
∴AC=sin∠AOC AO≈0.6428×1.2≈0.77米,
∵汽车靠墙一侧OB与墙MN平行且距离为0.8米,
∴车门不会碰到墙.
(2)当靠墙一侧的车门能打开的最大角度时,AC=0.8米,
∵sin∠AOC==≈0.67,
∴∠AOC≈42°.
答:靠墙一侧的车门能打开的最大角度约为42°.
5.解:(1)①过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,
则点C到直线DE的距离为CF,
在Rt△CDF中,
∵sin∠CDE=,
∴CF=CD sin60°=70×=35(mm).
②由图可知,点A到直线DE的距离为:AH+CF.
∵∠DCB=70°,
∴∠ACD=180°﹣∠DCB=110°,
∵CG∥DE,
∴∠GCD=∠CDE=60°.
∴∠ACH=∠ACD﹣∠DCG=50°.
在Rt△ACH中,
∵sin∠ACH=,
∴AH=AC sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm),
∴点A到直线DE的距离为AH+CF=35+64=123.5≈124(mm).
(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,
则B′C′=BC=35mm,DC′=DC=70mm.
在Rt△B′C′D中,
∵tan∠B′DC′===0.5,tan26.6°≈0.5,
∴∠B′DC′=26.6°.
∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.
故答案为:33.4°.
三.解直角三角形的应用-坡度坡角问题
6.解:因为sinθ=,
所以l=.
故选:B.
7.解:如图.∵在Rt△ABC中,∠ACB=90°,tanα=,
∴可设AC=4xm,那么BC=3xm,
∴AB==5xm,
∴A′B′=AB=5x(m).
∵在Rt△A′B′C中,∠A′CB′=90°,A′C=(4x﹣1)m,B′C=(3x+1)m,
∴(4x﹣1)2+(3x+1)2=(5x)2,
解得x=1,
∴A′C=3m,B′C=4m,A′B′=5m,
∴cosβ=.
故选:A.
8.解:∵迎水坡AB的坡比为1:,
∴=,即=,
解得,AC=3,
由勾股定理得,AB==6(m),
故选:A.
9.解:在Rt△ABC中,cosA=,
则梯子底端到墙角的距离AC=AB cosA=5cos40°,
故选:A.
10.解:如图,延长BC交AD于F,过F作FG⊥CD于G,
∵斜坡CE的坡度为i(即tanα)=1:,
∴α=30°.
∵BF∥EM,
∴∠FCD=∠E=30°.
∵∠AFB=60°.
∴∠CDF=∠AFB﹣∠FCD=30°.
∴∠ECD=∠FDC=30°.
∴FC=FD.
∴CG=CD=.
∴CF===5(米).
∴BF=BC+CF=15+5=20(米).
∴AB=BF tan60°=20(米).
答:建筑物AB的高度是20米.
四.解直角三角形的应用-仰角俯角问题
11.解:(1)作DG⊥AC于点G,
由题意可得,∠1=32°,∠2=45°,
∴∠CDG=32°,∠ADG=45°,
∴∠ADG=∠DAG=45°,
∴GD=GA,
设CG=x米,则AG=BC﹣BA﹣CG=57.8﹣1.6﹣x=(56.2﹣x)米,
则GD=(56.2﹣x)米,
∵tan∠CGD=,
∴tan32°=,
解得x≈21.6,
∴BG=BC﹣GC≈57.8﹣21.6=36.2(米),
∴MN=BG=36.2米,
答:旅游服务中心的高度约为36.2米;
(2)造成误差的主要原因有系统误差和随机误差,比如误读、误算、视差、刻度误差等,避免或者减小差距可以通过多次测量,求平均值.
12.解:过点 PD作 DE⊥AC 交 AC于点 E,DF⊥AB交 AB于点 F,
∵i=1:3,CD=10,
设 DE=xm,则 CE=3xm,
在 Rt△CED 中,x2+(3x)2=102,
解得:x=或x=﹣(舍),
∴DE=m,则CE=3m,
∵∠BDF=∠DBF=45°,
∴BF=DF,
设 BF=DF=m 米,则 AB=(m+)米,AC=(m﹣3)米,
在 Rt△CAB 中,,
解得:m≈29.9,
∴AB=29.9+≈33.1(米),
答:塑像的高度约为 33.1米.
13.解:(1)如图,延长CE交AB于点G,
则四边形CDFE和四边形EFBG是矩形,
根据题意可知:α=29°,β=60°.CD=EF=GB=1.6m,DF=20m,
设FG=x,
在Rt△AEG中,
∵∠AEG=β=60°,
∴∠EAG=30°,
∴AG=x,
在Rt△ACG中,
∵tanα=,
∴≈0.55,
∴x≈9.3,
∴AG≈9.3(m),
∴AB=AG+GB=9.3+1.6=10.9(m),
答:旗杆高度为10.9m;
(2)原因:小明测量的只是测角器所在位置与旗杆底座正方体边缘的最短距离,不是测量测角器所在位置与底座中心的最短距离.
14.解:设CD=xm,
∵∠ACD=60°,∠BCD=45°,
∴AD=x tan60=x(m),DB=x tan45°=x(m),
∵∠AED=30°,DE=6m,
∴AD=DE tan30°=6×=2(m),
∴x=2,
解得x=2(m),
∴AB=AD+DB=x+x=(2+2)m.
答:雕像AB的高度为(2+2)m.
15.解:由题意得,BD=50km,∠ADB=37°,DE=15km,∠AEC=56°,
在Rt△ABD中,
∵BD=50km,∠ADB=37°,
∴AB=sin37°×BD≈×50=30(km),AD=cos37°×BD≈×50=40(km),
∴AE=AD﹣DE=40﹣15=25(km),
在Rt△AEC中,∠AEC=56°,
∴AC=tan56°×AE≈×25=37(km),
∴BC=AC﹣AB=37﹣20≈17(km),
∴火箭的速度为17÷10≈1.7(km/s),
答:运载火箭从B处到C处时的平均速度约为1.7km/s.
五.解直角三角形的应用-仰角俯角问题
16.解:(1)如图,延长EF交CD于点G.
由题意知,四边形ABFE和四边形BCGF均为矩形.
∴EF=AB=100m,BC=FG,AE=BF=CG=1m,
设BC=FG=xm,则EG=(100+x) m.
在Rt△DEG中,
∵∠DEG=60°,
∴DG=EG tan60°=(100+x)≈1.73(100+x) m.
在Rt△DFG中,
∵∠DFG=72.3°,
∴DG=FG tan72.3°≈3.13x(m),
∴1.73(100+x)=3.13x,
解得x=123.57.
∴CD=DG+CG≈3.13×123.57+1≈387.8(m).
答:中原福塔CD的高度约为387.8m.(注:解法不同,答案会有误差,合理即可).
(2)误差为388﹣387.8=0.2(m).
减小误差可多次测量,去测量数据的平均值(答案不唯一,合理即可).
六.解直角三角形的应用-方向角问题
17.解:过点C作CD⊥AB交AB的延长线于D,
由题意得,AB=40×=20,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠CBD﹣∠CAB=30°,
∴∠ACB=∠CAB,
∴CB=AB=20,
在Rt△CBD中,sin∠CBD=,
∴CD=BC sin∠CBD=20×=10,
∵10<18,
∴这艘渔船继续向东追赶鱼群,有着弹危险.
18.解:过点P作PD⊥AB于D点,
由题意知,AB∥EF,∠ADP=∠BDP=90°,AP=80nmile,
∴∠A=∠EPA=60°,∠B=∠BPF=37°,
Rt△ADP中,∵sinA=,
∴PD=AP sinA=AP sin60°=(nmile),
Rt△BDP中,∵sinB=,
∴(nmile),
答:轮船所在B处与灯塔P的距离约为113nmile.
19.解:(1)作BD⊥AC于D.
依题意得,
∠BAE=45°,∠ABC=105°,∠CAE=15°,
∴∠BAC=30°,
∴∠ACB=45°.
在Rt△BCD中,∠BDC=90°,∠ACB=45°,
∴∠CBD=45°,
∴∠CBD=∠DCB,
∴BD=CD,
设BD=xkm,则CD=xkm,
在Rt△ABD中,∠BAC=30°,
∴AB=2BD=2xkm,tan30°=,
∴=,
∴AD=x,
在Rt△BDC中,∠BDC=90°,∠DCB=45°,
∴sin∠DCB==,
∴BC=x,
∵CD+AD=30+30,
∴x+x=30+30,
∴x=30,
∴AB=2x=60(km);
(2)第二组先到达目的地,
理由:∵BD=30km,
∴BC=x=30km,
第一组用时:60÷40=1.5(h);第二组用时:30÷35=(h),
∵<1.5,
∴第二组先到达目的地,
答:第二组先到达目的地.
知识点分类训练(附答案)
一.解直角三角形
1.如图,在平面直角坐标系中,AB=3,连接AB并延长至C,连接OC,若满足OC2=BC AC,tanα=2,则点C的坐标为 .
二.解直角三角形的应用
2.图1是挂墙式淋浴花洒的实物图,图2是抽象出来的几何图形.为使身高175cm的人能方便地淋浴,应当使旋转头固定在墙上的某个位置O,花洒的最高点B与人的头顶的铅垂距离为15cm,已知龙头手柄OA长为10cm,花洒直径AB是8cm,龙头手柄与墙面的较小夹角∠COA=26°,∠OAB=146°,则安装时,旋转头的固定点O与地面的距离应为多少?(计算结果精确到1cm,参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
3.图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.
(1)求∠ABC的度数;
(2)测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,≈1.414)
4.如图1,是一辆小汽车与墙平行停放的实物图片,图2是它的俯视图.汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米.(参考数据:sin40°≈0.6428,cos40°≈0.7660,sin41°≈0.6561,cos41°≈0.7547,sin42°≈0.6691,cos42°≈0.7431)
(1)当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.
(2)若车停在原地不动,靠墙一侧的车门能打开的最大角度约为多少?
5.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动.
(1)当∠CDE=60°时,
①求点C到直线DE的距离(计算结果保留根号);
②若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,则CD旋转的角度为 .(直接写出结果)
(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
三.解直角三角形的应用-坡度坡角问题
6.如图,某超市的自动扶梯高为h(m),坡角为θ,那么扶梯长l(m)为( )
A.hcosθ B. C.htanθ D.
7.如图,AB是斜靠在墙上的长梯,AB与地面夹角为α,当梯顶A下滑1m到A′时,梯脚B滑到B′,A'B'与地面的夹角为β,若tanα=,BB'=1m,则cosβ=( )
A. B. C. D.
8.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.6m B.3m C.9m D.6m
9.一架5米长的梯子斜靠在墙上,测得它与地面的夹角为40°,则梯子底端到墙角的距离为( )
A.5cos40°米 B.5sin40°米 C.米 D.米
10.如图所示,建筑物AB坐落在一斜坡的坡顶的平地上,当太阳光线与水平线夹角成60°时,测得建筑物AB在坡顶平地上的一部分影子BC=15米,在斜坡CE上的另一部分影子CD=5米,且斜坡CE的坡度为i(即tanα)=1:,求建筑物AB的高度.(结果保留根号)
四.解直角三角形的应用-仰角俯角问题
11.许昌市旅游服务中心由广场和“一门四阙”主题建筑组成,如图1.广场为迎宾广场一门”为“许昌之门”,“四闕”为广场四角的汉阙,是许昌的标志性建筑.某数学兴趣小组在迎宾广场测量旅游服务中心的高度,图2为测量示意图,MN为服务中心的对称轴,在地面的AB处架设测角仪,测得旅游服务中心的最高点D的仰角45°,利用无人机在点B的正上方57.8米处的点C处测得点D的俯角为32°,测角仪的高度AB=1.6米,FH=17.2米,DE=19.8米.
(1)求旅游服务中心的高度为多少米?(结果精确到0.1m.参考数据:sin32°≈0.530,cos32°≈0.848,tan32°≈0.625,≈1.414)
(2)兴趣小组测量后到旅游服务中心参观,发现讲解员讲解的高度为36.8m,请用物理知识解释测量值与实际值出现差距的原因,如何避免或者减小差距?
12.大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建,某数学兴趣小组想测量底座之上部分雕像AB的高度,如图在和雕塑底座上端水平的山坡C处测得雕塑顶端B的仰角为58.5°,沿山坡上行10米到达点D,测得雕塑顶端B的仰角为45°,已知山坡的坡度i=1:3,且A,C在同一水平地面上,求塑像AB的高度.(测倾器高度忽略不计,结果精确到0.1米,参考数据:sin58.5°≈0.85,cos58.5°≈0.52,tan58.5°≈1.63,≈1.4,≈1.7,≈3.2.)
13.九年级数学兴趣小组的实践课题是“测量物体高度”.小组成员小明与小红分别采用不同的方案测量同一个底座为正方体的旗杆的高度.以下是他们研究报告的部分记录内容:
课题:测量旗杆高度
小明的研究报告 小红的研究报告
测量示意图
测量方案与测量数据 在点D处用距离地面高度为1.6m的测角仪测出旗杆顶端A的仰角α=55°,再用皮尺测得测角仪底部所在位置与旗杆底座正方体边缘的最短距离为10m. 在点D处用距离地面高度为1.6m的测角仪测出旗杆顶端A的仰角α=29°,然后沿DF方向走20m到达点F处,测出旗杆顶端A的仰角β=60°.
参考数据 sin55°≈0.82,cos55°=0.57,tan55°≈1.43, sin29°≈0.48,cos29°≈0.87,tan29°≈0.55,≈1.73
计算旗杆高度 10×tan55°+1.6≈15.9(m)
(1)写出小红研究报告中“计算旗杆高度”的解答过程(结果精确到0.1m);
(2)数学老师说小明的测量结果与旗杆实际高度偏差较大,超出了误差允许范围,请你针对小明的测量方案分析测量偏差较大的原因.
14.某校一初三学生在学习了“锐角三角函数”的应用后,来到“孔子圣像”的雕像前,如图,想要用所学知识解决“孔子圣像”雕像AB的高度,他在雕像前C处用自制测角仪测得顶端A的仰角为60°,底端B的俯角为45°;又在同一水平线上的E处用自制测角仪测得顶端A的仰角为30°,已知DE=6m,求雕像AB的高度.(结果保留根号)
15.2020年6月23日,北斗卫星最后一颗全球组网卫星发射成功.运载火箭从地面A处(忽略发射塔高度)竖直向上发射,当运载火箭到达点B处时,地面D处的雷达站测得B处仰角为37°,BD=50km.10秒后,运载火箭直线上升到达点C处,此时地面E处一观测点测得C处的仰角为56°,已知点A,D,E在同一条直线上,并且D,E两处相距15km,求运载火箭从B处到C处时的平均速度(单位:km/s).
(参考数值:sin37°≈,cos37°≈,tan37°≈,sin56°≈,cos56°≈,tan56°≈)
五.解直角三角形的应用-仰角俯角问题
16.中原福塔,又名“河南广播电视塔”,是郑州市著名地标之一.小明和小亮利用卷尺和自制的测角仪测量福塔的高度.如图,小明站在点A处测得福塔顶端D的仰角为60°,小亮站在点B处测得福塔顶端D的仰角为72.3°.已知测角仪高度为1m,两人相距100m(点A,B,C在一条直线上).
(1)求中原福塔CD的高度;(结果精确到0.1m.参考数据:sin72.3≈0.95,cos72.3≈0.30,tan72.3≈3.13,)
(2)“景点简介”显示,中原福塔总高388m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
六.解直角三角形的应用-方向角问题
17.如图,一艘渔船以40海里/小时的速度由西向东追赶鱼群,在A处测得小岛C在渔船的北偏东60°方向;半小时后,渔船到达B处,此时测得小岛C在渔船的北偏东30°方向.已知以小岛C为中心,周围18海里以内为军事演习着弹危险区.如果这艘渔船继续向东追赶鱼群,是否有着弹危险?
18.如图,一艘海轮船位于灯塔P北偏东60°方向,与灯塔距离为80nmile的A处,它沿正南方向航行一段时间后,到达位于灯塔P南偏东37°方向的B处,求此时轮船所在B处与灯塔P的距离.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.7,结果取整数)
19.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习.如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是35km/h.
(1)求学校到红色文化基地A的距离?
(2)哪组同学先到达目的地?请说明理由(结果保留根号).
参考答案
一.解直角三角形
1.解:∵∠C=∠C,
∵OC2=BC AC,
即,
∴△OBC∽△OAC,
∴∠A=∠COB,
∵α+∠COB=90°,∠A+∠ABO=90°,
∴∠ABO=α,
∵tanα=2,
∴tan∠ABO=,
∴OA=2OB,
∵AB=3,
由勾股定理可得:OA2+OB2=AB2,
即,
解得:OB=3,
∴OA=6.
∴tanA=.
如图,过点C作CD⊥x轴于点D,
∵tanα=2,
∴设C(﹣m,2m),m>0,
∴AD=6+m,
∵tan∠A=,
∴,
∴,
解得:m=2,
经检验,m=2是原方程的解.
∴点C坐标为:(﹣2,4).
故答案为:(﹣2,4).
二.解直角三角形的应用
2.解:如图,过点B作地面的垂线,垂足为D,过点 A作地面GD的平行线,交OC于点E,交BD于点F,
在Rt△AOE中,∠AOE=26°,OA=10cm,
则OE=OA cos∠AOE≈10×0.90=9cm,
在Rt△ABF中,∠BAF=146°﹣90°﹣26°=30°,AB=8cm,
则BF=AB sin∠BAF=8×=4cm,
∴OG=BD﹣BF﹣OE=(175+15)﹣4﹣9=177cm,
答:旋转头的固定点O与地面的距离约为177cm.
3.解:(1)过点B作BH⊥MP,垂足为H,过点M作MI⊥FG,垂足为I,过点P作PK⊥DE,垂足为K,
∵MP=25.3cm,BA=HP=8.5cm,
∴MH=MP﹣HP=25.3﹣8.5=16.8(cm),
在Rt△BMH中,
cos∠BMH===0.4,
∴∠BMH=66.4°,
∵AB∥MP,
∴∠BMH+∠ABC=180°,
∴∠ABC=180°﹣66.4°=113.6°;
(2)∵∠BMN=68.6°,∠BMH=66.4°,
∴∠NMI=180°﹣∠BMN﹣∠BMH=180°﹣68.6°﹣66.4°=45°,
∵MN=28cm,
∴cos45°==,
∴MI≈19.80cm,
∵KI=50cm,
∴PK=KI﹣MI﹣MP=50﹣19.80﹣25.3=4.90≈4.9(cm),
∴此时枪身端点A与小红额头的距离是在规定范围内.
4.解:(1)过点A作AC⊥OB,垂足为点C,
在Rt△ACO中,
∵∠AOC=40°,AO=1.2米,
∴AC=sin∠AOC AO≈0.6428×1.2≈0.77米,
∵汽车靠墙一侧OB与墙MN平行且距离为0.8米,
∴车门不会碰到墙.
(2)当靠墙一侧的车门能打开的最大角度时,AC=0.8米,
∵sin∠AOC==≈0.67,
∴∠AOC≈42°.
答:靠墙一侧的车门能打开的最大角度约为42°.
5.解:(1)①过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,
则点C到直线DE的距离为CF,
在Rt△CDF中,
∵sin∠CDE=,
∴CF=CD sin60°=70×=35(mm).
②由图可知,点A到直线DE的距离为:AH+CF.
∵∠DCB=70°,
∴∠ACD=180°﹣∠DCB=110°,
∵CG∥DE,
∴∠GCD=∠CDE=60°.
∴∠ACH=∠ACD﹣∠DCG=50°.
在Rt△ACH中,
∵sin∠ACH=,
∴AH=AC sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm),
∴点A到直线DE的距离为AH+CF=35+64=123.5≈124(mm).
(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,
则B′C′=BC=35mm,DC′=DC=70mm.
在Rt△B′C′D中,
∵tan∠B′DC′===0.5,tan26.6°≈0.5,
∴∠B′DC′=26.6°.
∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.
故答案为:33.4°.
三.解直角三角形的应用-坡度坡角问题
6.解:因为sinθ=,
所以l=.
故选:B.
7.解:如图.∵在Rt△ABC中,∠ACB=90°,tanα=,
∴可设AC=4xm,那么BC=3xm,
∴AB==5xm,
∴A′B′=AB=5x(m).
∵在Rt△A′B′C中,∠A′CB′=90°,A′C=(4x﹣1)m,B′C=(3x+1)m,
∴(4x﹣1)2+(3x+1)2=(5x)2,
解得x=1,
∴A′C=3m,B′C=4m,A′B′=5m,
∴cosβ=.
故选:A.
8.解:∵迎水坡AB的坡比为1:,
∴=,即=,
解得,AC=3,
由勾股定理得,AB==6(m),
故选:A.
9.解:在Rt△ABC中,cosA=,
则梯子底端到墙角的距离AC=AB cosA=5cos40°,
故选:A.
10.解:如图,延长BC交AD于F,过F作FG⊥CD于G,
∵斜坡CE的坡度为i(即tanα)=1:,
∴α=30°.
∵BF∥EM,
∴∠FCD=∠E=30°.
∵∠AFB=60°.
∴∠CDF=∠AFB﹣∠FCD=30°.
∴∠ECD=∠FDC=30°.
∴FC=FD.
∴CG=CD=.
∴CF===5(米).
∴BF=BC+CF=15+5=20(米).
∴AB=BF tan60°=20(米).
答:建筑物AB的高度是20米.
四.解直角三角形的应用-仰角俯角问题
11.解:(1)作DG⊥AC于点G,
由题意可得,∠1=32°,∠2=45°,
∴∠CDG=32°,∠ADG=45°,
∴∠ADG=∠DAG=45°,
∴GD=GA,
设CG=x米,则AG=BC﹣BA﹣CG=57.8﹣1.6﹣x=(56.2﹣x)米,
则GD=(56.2﹣x)米,
∵tan∠CGD=,
∴tan32°=,
解得x≈21.6,
∴BG=BC﹣GC≈57.8﹣21.6=36.2(米),
∴MN=BG=36.2米,
答:旅游服务中心的高度约为36.2米;
(2)造成误差的主要原因有系统误差和随机误差,比如误读、误算、视差、刻度误差等,避免或者减小差距可以通过多次测量,求平均值.
12.解:过点 PD作 DE⊥AC 交 AC于点 E,DF⊥AB交 AB于点 F,
∵i=1:3,CD=10,
设 DE=xm,则 CE=3xm,
在 Rt△CED 中,x2+(3x)2=102,
解得:x=或x=﹣(舍),
∴DE=m,则CE=3m,
∵∠BDF=∠DBF=45°,
∴BF=DF,
设 BF=DF=m 米,则 AB=(m+)米,AC=(m﹣3)米,
在 Rt△CAB 中,,
解得:m≈29.9,
∴AB=29.9+≈33.1(米),
答:塑像的高度约为 33.1米.
13.解:(1)如图,延长CE交AB于点G,
则四边形CDFE和四边形EFBG是矩形,
根据题意可知:α=29°,β=60°.CD=EF=GB=1.6m,DF=20m,
设FG=x,
在Rt△AEG中,
∵∠AEG=β=60°,
∴∠EAG=30°,
∴AG=x,
在Rt△ACG中,
∵tanα=,
∴≈0.55,
∴x≈9.3,
∴AG≈9.3(m),
∴AB=AG+GB=9.3+1.6=10.9(m),
答:旗杆高度为10.9m;
(2)原因:小明测量的只是测角器所在位置与旗杆底座正方体边缘的最短距离,不是测量测角器所在位置与底座中心的最短距离.
14.解:设CD=xm,
∵∠ACD=60°,∠BCD=45°,
∴AD=x tan60=x(m),DB=x tan45°=x(m),
∵∠AED=30°,DE=6m,
∴AD=DE tan30°=6×=2(m),
∴x=2,
解得x=2(m),
∴AB=AD+DB=x+x=(2+2)m.
答:雕像AB的高度为(2+2)m.
15.解:由题意得,BD=50km,∠ADB=37°,DE=15km,∠AEC=56°,
在Rt△ABD中,
∵BD=50km,∠ADB=37°,
∴AB=sin37°×BD≈×50=30(km),AD=cos37°×BD≈×50=40(km),
∴AE=AD﹣DE=40﹣15=25(km),
在Rt△AEC中,∠AEC=56°,
∴AC=tan56°×AE≈×25=37(km),
∴BC=AC﹣AB=37﹣20≈17(km),
∴火箭的速度为17÷10≈1.7(km/s),
答:运载火箭从B处到C处时的平均速度约为1.7km/s.
五.解直角三角形的应用-仰角俯角问题
16.解:(1)如图,延长EF交CD于点G.
由题意知,四边形ABFE和四边形BCGF均为矩形.
∴EF=AB=100m,BC=FG,AE=BF=CG=1m,
设BC=FG=xm,则EG=(100+x) m.
在Rt△DEG中,
∵∠DEG=60°,
∴DG=EG tan60°=(100+x)≈1.73(100+x) m.
在Rt△DFG中,
∵∠DFG=72.3°,
∴DG=FG tan72.3°≈3.13x(m),
∴1.73(100+x)=3.13x,
解得x=123.57.
∴CD=DG+CG≈3.13×123.57+1≈387.8(m).
答:中原福塔CD的高度约为387.8m.(注:解法不同,答案会有误差,合理即可).
(2)误差为388﹣387.8=0.2(m).
减小误差可多次测量,去测量数据的平均值(答案不唯一,合理即可).
六.解直角三角形的应用-方向角问题
17.解:过点C作CD⊥AB交AB的延长线于D,
由题意得,AB=40×=20,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠CBD﹣∠CAB=30°,
∴∠ACB=∠CAB,
∴CB=AB=20,
在Rt△CBD中,sin∠CBD=,
∴CD=BC sin∠CBD=20×=10,
∵10<18,
∴这艘渔船继续向东追赶鱼群,有着弹危险.
18.解:过点P作PD⊥AB于D点,
由题意知,AB∥EF,∠ADP=∠BDP=90°,AP=80nmile,
∴∠A=∠EPA=60°,∠B=∠BPF=37°,
Rt△ADP中,∵sinA=,
∴PD=AP sinA=AP sin60°=(nmile),
Rt△BDP中,∵sinB=,
∴(nmile),
答:轮船所在B处与灯塔P的距离约为113nmile.
19.解:(1)作BD⊥AC于D.
依题意得,
∠BAE=45°,∠ABC=105°,∠CAE=15°,
∴∠BAC=30°,
∴∠ACB=45°.
在Rt△BCD中,∠BDC=90°,∠ACB=45°,
∴∠CBD=45°,
∴∠CBD=∠DCB,
∴BD=CD,
设BD=xkm,则CD=xkm,
在Rt△ABD中,∠BAC=30°,
∴AB=2BD=2xkm,tan30°=,
∴=,
∴AD=x,
在Rt△BDC中,∠BDC=90°,∠DCB=45°,
∴sin∠DCB==,
∴BC=x,
∵CD+AD=30+30,
∴x+x=30+30,
∴x=30,
∴AB=2x=60(km);
(2)第二组先到达目的地,
理由:∵BD=30km,
∴BC=x=30km,
第一组用时:60÷40=1.5(h);第二组用时:30÷35=(h),
∵<1.5,
∴第二组先到达目的地,
答:第二组先到达目的地.
