北京课改版数学七年级下册第六章 整式的运算期末测试试卷(word版含答案)独家版权
文档属性
| 名称 | 北京课改版数学七年级下册第六章 整式的运算期末测试试卷(word版含答案)独家版权 |

|
|
| 格式 | zip | ||
| 文件大小 | 361.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览




文档简介
北京课改版数学七年级下册第六章 整式的运算期末测试试卷
一、选择题(共10小题;共50分)
1. 下列各式计算正确的是
A. B. C. D.
2. 下面计算中:① ;② ;③ ;④ ;⑤ ;⑥ .其中做对的题有
A. 道 B. 道 C. 道 D. 道
3. 等式 成立的条件是
A. B. C. D. 为有理数
4. 下列各式正确的是
A. B.
C. D.
5. 如图,长方形 的周长是 ,以 , 为边向外作正方形 和正方形 ,若正方形 和正方形 的面积之和为 ,那么长方形 的面积是
A. B. C. D.
6. 若 ,则
A. B. C. D.
7. 某校组织若干师生到恩施大峡谷进行社会实践活动,若学校租用 座的客车 辆,则余下 人无座位;若租用 座的客车则可少租用 辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是
A. B. C. D.
8. 计算 的结果是
A. B. C. D.
9. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图①可以得到 ,那么利用图②所得到的数学等式是
A.
B.
C.
D.
10. 我国宋朝数学家杨辉 年的著作《详解九章算法》给出了在 ( 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 若代数式 可以表示为 的形式,则 的值是 .
12. 若 ,则 的取值为 .
13. 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了 ( 为非负整数)的展开式中按 的次数从大到小排列的项的系数.例如, 展开式中的系数 ,, 恰好对应图中第三行的数字.
请认真观察此图,写出 的展开式: .
14. 下列是用科学记数法表示的数,写出原来的数.
() ;
() .
15. 某同学计算 的过程如下:
模仿这位同学的运算方法,计算:
.
16. 现规定 ,则 的值为 .
17. 如图,两个正方形的边长分别为 ,,若 ,,则阴影部分的面积为 .
18. 如图是我国数学家发明的“杨辉三角”,此图揭示了 ( 为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出 的展开式共有 项,第二项的系数是 , 的展开式共有 项,各项的系数和是 .
19. 设 , 是实数,定义关于“”的一种运算:,则下列结论:
①若 ,则 或 ;
②不存在实数 , 满足 ;
③ ;
④若 ,则 ,
其中正确的是 .(填写序号)
三、解答题(共6小题;共50分)
20. 计算:
(1);
(2);
(3).
21. 计算:
(1);
(2);
(3).
22. 阅读以下材料:;;;
(1)根据以上规律, ;
(2)利用()的结论,求 的值.
23. 已知x+y=7,xy=6,求:
(1)x﹣y的值;
(2) 的值.
24. 乘法公式的探究及应用.
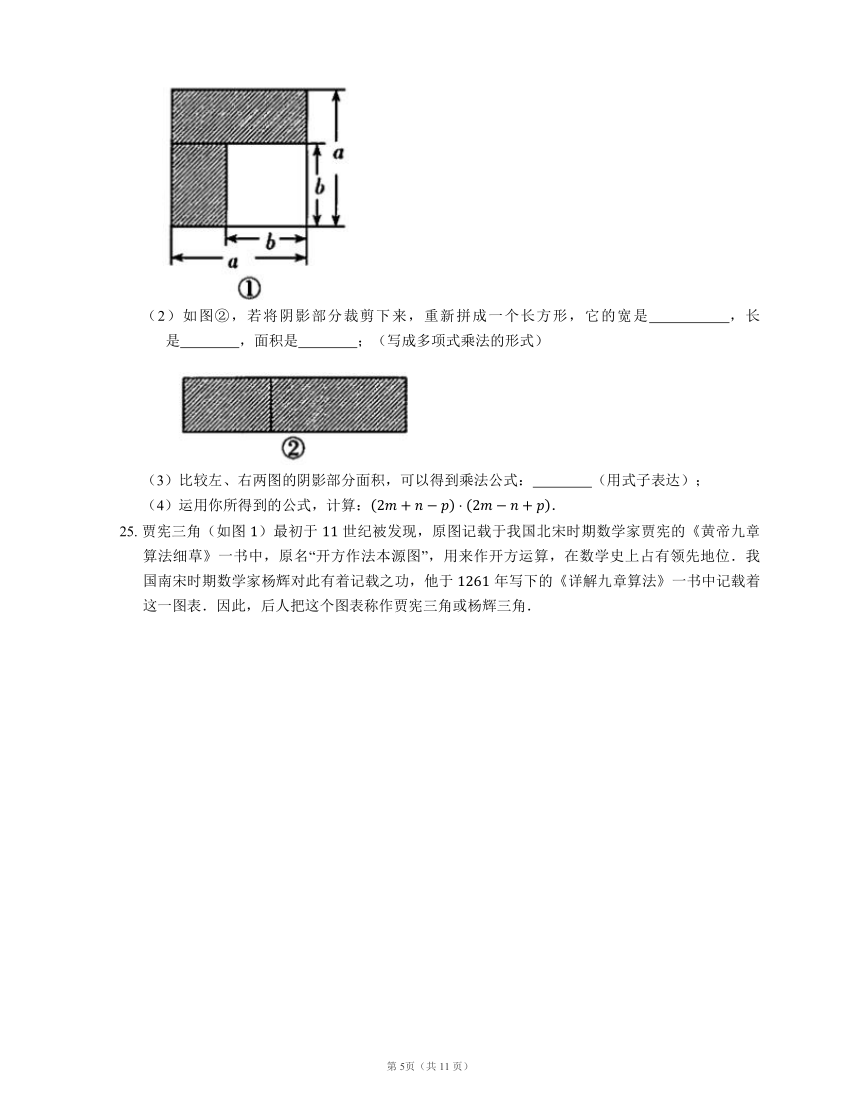
(1)如图①,可以求出阴影部分的面积是 ;(写成两数平方差的形式)
(2)如图②,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 ,长是 ,面积是 ;(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式: (用式子表达);
(4)运用你所得到的公式,计算:.
25. 贾宪三角(如图 )最初于 世纪被发现,原图记载于我国北宋时期数学家贾宪的《黄帝九章算法细草》一书中,原名“开方作法本源图”,用来作开方运算,在数学史上占有领先地位.我国南宋时期数学家杨辉对此有着记载之功,他于 年写下的《详解九章算法》一书中记载着这一图表.因此,后人把这个图表称作贾宪三角或杨辉三角.
施蒂费尔的二项式乘方后展开式的系数规律如图 所示.在贾宪三角中,第三行的三个数恰好对应着两数和的平方公式 展开式的系数.再如,第四行的四个数恰好对应着两数和的立方公式 展开式的系数,第五行的五个数恰好对应着两数和的四次方公式 展开式的系数,等等.由此可见,贾宪三角可以看成是对我们现在学习的两数和的平方公式的推广而得到的,根据以上材料解决下列问题:
(1) 展开式中项数共有 项;
(2)写出 的展开式: ;
(3)计算:
(4)若 ,求 的值.
答案
第一部分
1. D
2. B 【解析】① ,正确;
② ,错误;
③ ,错误;
④ ,错误;
⑤ ,错误;
⑥ ,正确.
正确的有 道.故B正确.
3. C
4. D
5. B
【解析】设 ,,
正方形 和正方形 的面积之和为 ,
,
长方形 的周长是 ,
,
,
,
,
,
长方形 的面积为 .
6. B
7. C 【解析】因为学校租用 座的客车 辆,则余下 人无座位,所以师生的总人数为 .又因为租用 座的客车则可少租用 辆,所以乘坐最后一辆 座客车的人数为 .
8. B
9. B 【解析】从整体看:正方形的面积 ,
从局部看:正方形的面积 ,
所以 .
10. D
【解析】由题意,,
可知,展开式中第二项为 ,
所以 展开式中含 项的系数是 .
第二部分
11.
【解析】
所以 ,.
所以 .
12.
【解析】因为 ,
所以 ,
则 .
13.
14. ,
15.
16.
【解析】
17.
【解析】当 , 时,
18. ,,,
【解析】 的展开式有 项; 的展开式有 项; 的展开式有 项; 故 的展开式共有 项.由题中规律得 的展开式中第二项的系数为 , 的展开式中第二项的系数为 ,故 的展开式中第二项的系数为 .
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
故 的展开式中各项的系数和为 .
19. ①③④
【解析】①
,
,
,
,
或 ,故①正确;
②设存在实数 , 满足题意.
,,
,
,
,
存在实数 , 满足 ,故②错误;
③
,,
,故③正确;
④
,
,
,
,故④正确.
综上,正确的是①③④.
第三部分
20. (1)
(2)
(3)
21. (1)
(2)
(3)
22. (1)
【解析】.
(2)
23. (1) ,
【解析】略
(2) 67 或 7
【解析】 当 时,原式 ;当 时,原式 .故 的值为 67 或 7 .
24. (1)
(2) ;;
(3)
(4)
25. (1)
(2)
(3)
(4) 当 时,,
当 时,,
.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 下列各式计算正确的是
A. B. C. D.
2. 下面计算中:① ;② ;③ ;④ ;⑤ ;⑥ .其中做对的题有
A. 道 B. 道 C. 道 D. 道
3. 等式 成立的条件是
A. B. C. D. 为有理数
4. 下列各式正确的是
A. B.
C. D.
5. 如图,长方形 的周长是 ,以 , 为边向外作正方形 和正方形 ,若正方形 和正方形 的面积之和为 ,那么长方形 的面积是
A. B. C. D.
6. 若 ,则
A. B. C. D.
7. 某校组织若干师生到恩施大峡谷进行社会实践活动,若学校租用 座的客车 辆,则余下 人无座位;若租用 座的客车则可少租用 辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是
A. B. C. D.
8. 计算 的结果是
A. B. C. D.
9. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图①可以得到 ,那么利用图②所得到的数学等式是
A.
B.
C.
D.
10. 我国宋朝数学家杨辉 年的著作《详解九章算法》给出了在 ( 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A. B. C. D.
二、填空题(共10小题;共50分)
11. 若代数式 可以表示为 的形式,则 的值是 .
12. 若 ,则 的取值为 .
13. 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了 ( 为非负整数)的展开式中按 的次数从大到小排列的项的系数.例如, 展开式中的系数 ,, 恰好对应图中第三行的数字.
请认真观察此图,写出 的展开式: .
14. 下列是用科学记数法表示的数,写出原来的数.
() ;
() .
15. 某同学计算 的过程如下:
模仿这位同学的运算方法,计算:
.
16. 现规定 ,则 的值为 .
17. 如图,两个正方形的边长分别为 ,,若 ,,则阴影部分的面积为 .
18. 如图是我国数学家发明的“杨辉三角”,此图揭示了 ( 为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出 的展开式共有 项,第二项的系数是 , 的展开式共有 项,各项的系数和是 .
19. 设 , 是实数,定义关于“”的一种运算:,则下列结论:
①若 ,则 或 ;
②不存在实数 , 满足 ;
③ ;
④若 ,则 ,
其中正确的是 .(填写序号)
三、解答题(共6小题;共50分)
20. 计算:
(1);
(2);
(3).
21. 计算:
(1);
(2);
(3).
22. 阅读以下材料:;;;
(1)根据以上规律, ;
(2)利用()的结论,求 的值.
23. 已知x+y=7,xy=6,求:
(1)x﹣y的值;
(2) 的值.
24. 乘法公式的探究及应用.
(1)如图①,可以求出阴影部分的面积是 ;(写成两数平方差的形式)
(2)如图②,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 ,长是 ,面积是 ;(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式: (用式子表达);
(4)运用你所得到的公式,计算:.
25. 贾宪三角(如图 )最初于 世纪被发现,原图记载于我国北宋时期数学家贾宪的《黄帝九章算法细草》一书中,原名“开方作法本源图”,用来作开方运算,在数学史上占有领先地位.我国南宋时期数学家杨辉对此有着记载之功,他于 年写下的《详解九章算法》一书中记载着这一图表.因此,后人把这个图表称作贾宪三角或杨辉三角.
施蒂费尔的二项式乘方后展开式的系数规律如图 所示.在贾宪三角中,第三行的三个数恰好对应着两数和的平方公式 展开式的系数.再如,第四行的四个数恰好对应着两数和的立方公式 展开式的系数,第五行的五个数恰好对应着两数和的四次方公式 展开式的系数,等等.由此可见,贾宪三角可以看成是对我们现在学习的两数和的平方公式的推广而得到的,根据以上材料解决下列问题:
(1) 展开式中项数共有 项;
(2)写出 的展开式: ;
(3)计算:
(4)若 ,求 的值.
答案
第一部分
1. D
2. B 【解析】① ,正确;
② ,错误;
③ ,错误;
④ ,错误;
⑤ ,错误;
⑥ ,正确.
正确的有 道.故B正确.
3. C
4. D
5. B
【解析】设 ,,
正方形 和正方形 的面积之和为 ,
,
长方形 的周长是 ,
,
,
,
,
,
长方形 的面积为 .
6. B
7. C 【解析】因为学校租用 座的客车 辆,则余下 人无座位,所以师生的总人数为 .又因为租用 座的客车则可少租用 辆,所以乘坐最后一辆 座客车的人数为 .
8. B
9. B 【解析】从整体看:正方形的面积 ,
从局部看:正方形的面积 ,
所以 .
10. D
【解析】由题意,,
可知,展开式中第二项为 ,
所以 展开式中含 项的系数是 .
第二部分
11.
【解析】
所以 ,.
所以 .
12.
【解析】因为 ,
所以 ,
则 .
13.
14. ,
15.
16.
【解析】
17.
【解析】当 , 时,
18. ,,,
【解析】 的展开式有 项; 的展开式有 项; 的展开式有 项; 故 的展开式共有 项.由题中规律得 的展开式中第二项的系数为 , 的展开式中第二项的系数为 ,故 的展开式中第二项的系数为 .
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
故 的展开式中各项的系数和为 .
19. ①③④
【解析】①
,
,
,
,
或 ,故①正确;
②设存在实数 , 满足题意.
,,
,
,
,
存在实数 , 满足 ,故②错误;
③
,,
,故③正确;
④
,
,
,
,故④正确.
综上,正确的是①③④.
第三部分
20. (1)
(2)
(3)
21. (1)
(2)
(3)
22. (1)
【解析】.
(2)
23. (1) ,
【解析】略
(2) 67 或 7
【解析】 当 时,原式 ;当 时,原式 .故 的值为 67 或 7 .
24. (1)
(2) ;;
(3)
(4)
25. (1)
(2)
(3)
(4) 当 时,,
当 时,,
.
第1页(共1 页)
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
