2021-2022学年高二上学期数学沪教版(2020)必修第三册12.3 频率与概率“四基”测试题
文档属性
| 名称 | 2021-2022学年高二上学期数学沪教版(2020)必修第三册12.3 频率与概率“四基”测试题 |  | |
| 格式 | doc | ||
| 文件大小 | 237.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 09:38:45 | ||
图片预览



文档简介
四基:基础知识、基本技能、基本思想、基本活动经验 【建议用时:40分钟】
【学生版】
《 第12 章 概率初步》【12.3 频率与概率】
一、选择题(每小题6分,共12分)
1、以下是表述“频率”与“概率”的语句:
①在大量试验中,事件出现的频率与其概率很接近;
②概率可以作为当实验次数无限增大时频率的极限;
③计算频率通常是为了估计概率;.
其中正确的语句为( )
A.①② B.①③ C.②③ D.①②③
【提示】
【答案】
【解析】
【考点】
2、在给病人动手术之前,外科医生会告知病人或家属一些情况,其中有一项是说这种手术的成功率大约是99%.下列解释正确的是( )
A.100个手术有99个手术成功,有1个手术失败
B.这个手术一定成功
C.99%的医生能做这个手术,另外1%的医生不能做这个手术
D.这个手术成功的可能性大小是99%
【提示】
【答案】
【解析】
【考点】
二、填充题(每小题10分,共60分)
3、设某厂产品的次品率为2%,估算该厂8 000件产品中合格品的件数可能为 件。
【提示】
【答案】
【解析】
【考点】
4、抛掷一枚质地均匀的硬币1 000次,那么第999次出现正面朝上的概率是
【提示】
【答案】
【解析】
【考点】
5、某人抛掷一枚硬币100次,结果正面朝上53次,设正面朝上为事件A,则事件A出现的频数为________,事件A出现的频率为________。
【提示】
【答案】
【考点】
6、如果袋中装有数量差别很大而大小相同的白球和黄球(只是颜色不同)若干个,从中任取1球,取了10次有7个白球,估计袋中数量较多的是________球。
【提示】
【答案】
【解析】
【考点】
7、某射击运动员在同一条件下射击的成绩记录如表所示:
射击次数 50 100 200 400 1000
射中8环以上的次数 44 78 158 320 800
根据表中的数据,估计该射击运动员射击一次射中8环以上的概率为
【提示】
【答案】
【解析】
【考点】
8、某中学举办电脑知识竞赛,满分为100分,80分以上为优秀(含80分),现将高一两个班参赛学生的成绩进行整理后分成五组:第一组,第二组,第三组,第四组,第五组,其中第一 三 四 五小组的频率分别为,,,,而第二小组的频数是40,则参赛的人数以是 及成绩优秀的概率是
三、解答题(第9题12分,第10题16分)
9、下面是某批乒乓球质量检查结果表:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率
(1)在上表中填上优等品出现的频率;
(2)估计该批乒乓球优等品的概率是多少?
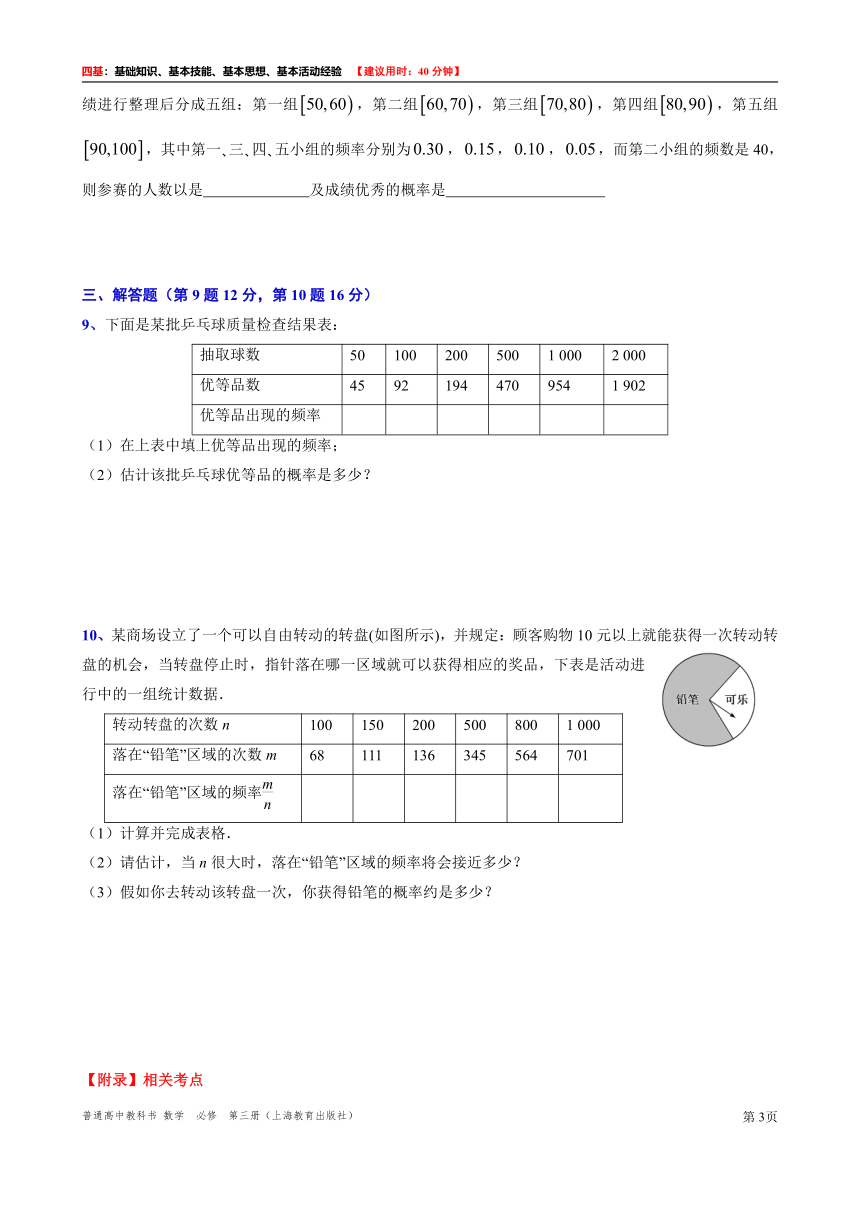
10、某商场设立了一个可以自由转动的转盘(如图所示),并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
转动转盘的次数n 100 150 200 500 800 1 000
落在“铅笔”区域的次数m 68 111 136 345 564 701
落在“铅笔”区域的频率
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
【附录】相关考点
考点一 伯努利试验 如果一个随机试验只有两种可能的结果,一个是“成功”,概率是:,一个是“失败”,概率是:,那么这个随机试验称为伯努利试验;
考点二 频率 假设我们可以独立地重复一个伯努利试验次,其中成功的次数记作,那么就被称为(次试验中)成功的频率;频率是一个数,依赖于试验次数;它不是一个确定的数,而是一个随机的数;
考点三 伯努利大数定律 伯努利大数定律:独立地重复一个伯努利试验次,当很大时,频率逼近概率;
【教师版】
《 第12 章 概率初步》【12.3 频率与概率】
一、选择题(每小题6分,共12分)
1、以下是表述“频率”与“概率”的语句:
①在大量试验中,事件出现的频率与其概率很接近;
②概率可以作为当实验次数无限增大时频率的极限;
③计算频率通常是为了估计概率;.
其中正确的语句为( )
A.①② B.①③ C.②③ D.①②③
【提示】由频率和概率的定义以及频率和概率的关系判断①②③,即可得正确答案;
【答案】D;
【解析】事件的频率是指事件发生的频数与次事件中事件出现的次数比,
随机事件在每次实验中是否会发生是不能预料的,但在大量重复试验后,随着试验次数的增加,事件发生的频率会逐渐稳定在区间中的某个常数上,这个常数就是事件的概率;所以随着试验次数的增加,频率一般会越来越接近概率;计算频率通常是为了估计概率;
所以①②③都正确,
【考点】概率、伯努利大数定律;辨析频率与概率的关系;
2、在给病人动手术之前,外科医生会告知病人或家属一些情况,其中有一项是说这种手术的成功率大约是99%.下列解释正确的是( )
A.100个手术有99个手术成功,有1个手术失败
B.这个手术一定成功
C.99%的医生能做这个手术,另外1%的医生不能做这个手术
D.这个手术成功的可能性大小是99%
【提示】理解频率的定义;
【答案】D;
【解析】成功率大约是99%,说明手术成功的可能性大小是99%,故选D;
【考点】概率;
二、填充题(每小题10分,共60分)
3、设某厂产品的次品率为2%,估算该厂8 000件产品中合格品的件数可能为 件。
【提示】理解做什么试验;
【答案】7 840;
【解析】8 000×(1-2%)=7 840(件);
【考点】伯努利试验
4、抛掷一枚质地均匀的硬币1 000次,那么第999次出现正面朝上的概率是
【提示】理解概率与频率的关系;
【答案】;
【解析】抛掷一枚质地均匀的硬币1 000次,每一次出现正面朝上的概率均为;
【考点】伯努利大数定律;
5、某人抛掷一枚硬币100次,结果正面朝上53次,设正面朝上为事件A,则事件A出现的频数为________,事件A出现的频率为________。
【提示】理解频率的定义;
【答案】53;0.53;
【考点】频率;
6、如果袋中装有数量差别很大而大小相同的白球和黄球(只是颜色不同)若干个,从中任取1球,取了10次有7个白球,估计袋中数量较多的是________球。
【提示】注意:做什么试验;
【答案】白;
【解析】取10次球有7次是白球,则取出白球的频率是0.7,故可估计袋中数量较多的是白球;
【考点】频率;
7、某射击运动员在同一条件下射击的成绩记录如表所示:
射击次数 50 100 200 400 1000
射中8环以上的次数 44 78 158 320 800
根据表中的数据,估计该射击运动员射击一次射中8环以上的概率为
【提示】会根据题意处理数据,利用频率估计概率即可求解;
【答案】0.80;
【解析】大量重复试验,由表格知射击运动员射中8环以上的频率稳定在,所以这名运动员射击一次射中8环以上的概率为;
【考点】伯努利大数定律;
8、某中学举办电脑知识竞赛,满分为100分,80分以上为优秀(含80分),现将高一两个班参赛学生的成绩进行整理后分成五组:第一组,第二组,第三组,第四组,第五组,其中第一 三 四 五小组的频率分别为,,,,而第二小组的频数是40,则参赛的人数以是 及成绩优秀的概率是
【提示】仔细阅读,准确处理数据;由于所有组的频率和为1,从而可求出第二组的频率,再由第二组的频数可求出总人数,求出成绩优秀的频率可得其概率;
【答案】100,;
【解析】由已知得第二小组的频率是,频数为40,
设共有参赛学生x人,则,所以.
因为成绩优秀的频率为,
所以成绩优秀的概率为;
【考点】频率;此题考查频率和频数的关系,考查频率与概率的关系;
三、解答题(第9题12分,第10题16分)
9、下面是某批乒乓球质量检查结果表:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率
(1)在上表中填上优等品出现的频率;
(2)估计该批乒乓球优等品的概率是多少?
【提示】理解频率的定义与求法;
【解析】如下表所示:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率 0.9 0.92 0.97 0.94 0.954 0.951
(2)从表中数据可以看出,这批乒乓球优等品的概率是0.95;
【考点】概率与频率及其关系;用频率估计概率1、频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率.频率本身是随机变量,当n很大时,频率总是在一个稳定值附近左右摆动,这个稳定值就是概率;2、解此类题目的步骤是:先利用频率的计算公式依次计算频率,然后用频率估计概率
10、某商场设立了一个可以自由转动的转盘(如图所示),并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
转动转盘的次数n 100 150 200 500 800 1 000
落在“铅笔”区域的次数m 68 111 136 345 564 701
落在“铅笔”区域的频率
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
【解析】
(1)如下表所示:
转动转盘的次数n 100 150 200 500 800 1 000
落在“铅笔”区域的次数m 68 111 136 345 564 701
落在“铅笔”区域的频率 0.68 0.74 0.68 0.69 0.705 0.701
(2)当n很大时,落在“铅笔”区域的频率将会接近0.7;
(3)获得铅笔的概率约是0.7;
【考点】概率与频率及其关系;伯努利大数定律;
【附录】相关考点
考点一 伯努利试验 如果一个随机试验只有两种可能的结果,一个是“成功”,概率是:,一个是“失败”,概率是:,那么这个随机试验称为伯努利试验;
考点二 频率 假设我们可以独立地重复一个伯努利试验次,其中成功的次数记作,那么就被称为(次试验中)成功的频率;频率是一个数,依赖于试验次数;它不是一个确定的数,而是一个随机的数;
考点三 伯努利大数定律 伯努利大数定律:独立地重复一个伯努利试验次,当很大时,频率逼近概率;
PAGE
第1页
普通高中教科书 数学 必修 第三册(上海教育出版社)
【学生版】
《 第12 章 概率初步》【12.3 频率与概率】
一、选择题(每小题6分,共12分)
1、以下是表述“频率”与“概率”的语句:
①在大量试验中,事件出现的频率与其概率很接近;
②概率可以作为当实验次数无限增大时频率的极限;
③计算频率通常是为了估计概率;.
其中正确的语句为( )
A.①② B.①③ C.②③ D.①②③
【提示】
【答案】
【解析】
【考点】
2、在给病人动手术之前,外科医生会告知病人或家属一些情况,其中有一项是说这种手术的成功率大约是99%.下列解释正确的是( )
A.100个手术有99个手术成功,有1个手术失败
B.这个手术一定成功
C.99%的医生能做这个手术,另外1%的医生不能做这个手术
D.这个手术成功的可能性大小是99%
【提示】
【答案】
【解析】
【考点】
二、填充题(每小题10分,共60分)
3、设某厂产品的次品率为2%,估算该厂8 000件产品中合格品的件数可能为 件。
【提示】
【答案】
【解析】
【考点】
4、抛掷一枚质地均匀的硬币1 000次,那么第999次出现正面朝上的概率是
【提示】
【答案】
【解析】
【考点】
5、某人抛掷一枚硬币100次,结果正面朝上53次,设正面朝上为事件A,则事件A出现的频数为________,事件A出现的频率为________。
【提示】
【答案】
【考点】
6、如果袋中装有数量差别很大而大小相同的白球和黄球(只是颜色不同)若干个,从中任取1球,取了10次有7个白球,估计袋中数量较多的是________球。
【提示】
【答案】
【解析】
【考点】
7、某射击运动员在同一条件下射击的成绩记录如表所示:
射击次数 50 100 200 400 1000
射中8环以上的次数 44 78 158 320 800
根据表中的数据,估计该射击运动员射击一次射中8环以上的概率为
【提示】
【答案】
【解析】
【考点】
8、某中学举办电脑知识竞赛,满分为100分,80分以上为优秀(含80分),现将高一两个班参赛学生的成绩进行整理后分成五组:第一组,第二组,第三组,第四组,第五组,其中第一 三 四 五小组的频率分别为,,,,而第二小组的频数是40,则参赛的人数以是 及成绩优秀的概率是
三、解答题(第9题12分,第10题16分)
9、下面是某批乒乓球质量检查结果表:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率
(1)在上表中填上优等品出现的频率;
(2)估计该批乒乓球优等品的概率是多少?
10、某商场设立了一个可以自由转动的转盘(如图所示),并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
转动转盘的次数n 100 150 200 500 800 1 000
落在“铅笔”区域的次数m 68 111 136 345 564 701
落在“铅笔”区域的频率
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
【附录】相关考点
考点一 伯努利试验 如果一个随机试验只有两种可能的结果,一个是“成功”,概率是:,一个是“失败”,概率是:,那么这个随机试验称为伯努利试验;
考点二 频率 假设我们可以独立地重复一个伯努利试验次,其中成功的次数记作,那么就被称为(次试验中)成功的频率;频率是一个数,依赖于试验次数;它不是一个确定的数,而是一个随机的数;
考点三 伯努利大数定律 伯努利大数定律:独立地重复一个伯努利试验次,当很大时,频率逼近概率;
【教师版】
《 第12 章 概率初步》【12.3 频率与概率】
一、选择题(每小题6分,共12分)
1、以下是表述“频率”与“概率”的语句:
①在大量试验中,事件出现的频率与其概率很接近;
②概率可以作为当实验次数无限增大时频率的极限;
③计算频率通常是为了估计概率;.
其中正确的语句为( )
A.①② B.①③ C.②③ D.①②③
【提示】由频率和概率的定义以及频率和概率的关系判断①②③,即可得正确答案;
【答案】D;
【解析】事件的频率是指事件发生的频数与次事件中事件出现的次数比,
随机事件在每次实验中是否会发生是不能预料的,但在大量重复试验后,随着试验次数的增加,事件发生的频率会逐渐稳定在区间中的某个常数上,这个常数就是事件的概率;所以随着试验次数的增加,频率一般会越来越接近概率;计算频率通常是为了估计概率;
所以①②③都正确,
【考点】概率、伯努利大数定律;辨析频率与概率的关系;
2、在给病人动手术之前,外科医生会告知病人或家属一些情况,其中有一项是说这种手术的成功率大约是99%.下列解释正确的是( )
A.100个手术有99个手术成功,有1个手术失败
B.这个手术一定成功
C.99%的医生能做这个手术,另外1%的医生不能做这个手术
D.这个手术成功的可能性大小是99%
【提示】理解频率的定义;
【答案】D;
【解析】成功率大约是99%,说明手术成功的可能性大小是99%,故选D;
【考点】概率;
二、填充题(每小题10分,共60分)
3、设某厂产品的次品率为2%,估算该厂8 000件产品中合格品的件数可能为 件。
【提示】理解做什么试验;
【答案】7 840;
【解析】8 000×(1-2%)=7 840(件);
【考点】伯努利试验
4、抛掷一枚质地均匀的硬币1 000次,那么第999次出现正面朝上的概率是
【提示】理解概率与频率的关系;
【答案】;
【解析】抛掷一枚质地均匀的硬币1 000次,每一次出现正面朝上的概率均为;
【考点】伯努利大数定律;
5、某人抛掷一枚硬币100次,结果正面朝上53次,设正面朝上为事件A,则事件A出现的频数为________,事件A出现的频率为________。
【提示】理解频率的定义;
【答案】53;0.53;
【考点】频率;
6、如果袋中装有数量差别很大而大小相同的白球和黄球(只是颜色不同)若干个,从中任取1球,取了10次有7个白球,估计袋中数量较多的是________球。
【提示】注意:做什么试验;
【答案】白;
【解析】取10次球有7次是白球,则取出白球的频率是0.7,故可估计袋中数量较多的是白球;
【考点】频率;
7、某射击运动员在同一条件下射击的成绩记录如表所示:
射击次数 50 100 200 400 1000
射中8环以上的次数 44 78 158 320 800
根据表中的数据,估计该射击运动员射击一次射中8环以上的概率为
【提示】会根据题意处理数据,利用频率估计概率即可求解;
【答案】0.80;
【解析】大量重复试验,由表格知射击运动员射中8环以上的频率稳定在,所以这名运动员射击一次射中8环以上的概率为;
【考点】伯努利大数定律;
8、某中学举办电脑知识竞赛,满分为100分,80分以上为优秀(含80分),现将高一两个班参赛学生的成绩进行整理后分成五组:第一组,第二组,第三组,第四组,第五组,其中第一 三 四 五小组的频率分别为,,,,而第二小组的频数是40,则参赛的人数以是 及成绩优秀的概率是
【提示】仔细阅读,准确处理数据;由于所有组的频率和为1,从而可求出第二组的频率,再由第二组的频数可求出总人数,求出成绩优秀的频率可得其概率;
【答案】100,;
【解析】由已知得第二小组的频率是,频数为40,
设共有参赛学生x人,则,所以.
因为成绩优秀的频率为,
所以成绩优秀的概率为;
【考点】频率;此题考查频率和频数的关系,考查频率与概率的关系;
三、解答题(第9题12分,第10题16分)
9、下面是某批乒乓球质量检查结果表:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率
(1)在上表中填上优等品出现的频率;
(2)估计该批乒乓球优等品的概率是多少?
【提示】理解频率的定义与求法;
【解析】如下表所示:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率 0.9 0.92 0.97 0.94 0.954 0.951
(2)从表中数据可以看出,这批乒乓球优等品的概率是0.95;
【考点】概率与频率及其关系;用频率估计概率1、频率是事件A发生的次数m与试验总次数n的比值,利用此公式可求出它们的频率.频率本身是随机变量,当n很大时,频率总是在一个稳定值附近左右摆动,这个稳定值就是概率;2、解此类题目的步骤是:先利用频率的计算公式依次计算频率,然后用频率估计概率
10、某商场设立了一个可以自由转动的转盘(如图所示),并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
转动转盘的次数n 100 150 200 500 800 1 000
落在“铅笔”区域的次数m 68 111 136 345 564 701
落在“铅笔”区域的频率
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
【解析】
(1)如下表所示:
转动转盘的次数n 100 150 200 500 800 1 000
落在“铅笔”区域的次数m 68 111 136 345 564 701
落在“铅笔”区域的频率 0.68 0.74 0.68 0.69 0.705 0.701
(2)当n很大时,落在“铅笔”区域的频率将会接近0.7;
(3)获得铅笔的概率约是0.7;
【考点】概率与频率及其关系;伯努利大数定律;
【附录】相关考点
考点一 伯努利试验 如果一个随机试验只有两种可能的结果,一个是“成功”,概率是:,一个是“失败”,概率是:,那么这个随机试验称为伯努利试验;
考点二 频率 假设我们可以独立地重复一个伯努利试验次,其中成功的次数记作,那么就被称为(次试验中)成功的频率;频率是一个数,依赖于试验次数;它不是一个确定的数,而是一个随机的数;
考点三 伯努利大数定律 伯努利大数定律:独立地重复一个伯努利试验次,当很大时,频率逼近概率;
PAGE
第1页
普通高中教科书 数学 必修 第三册(上海教育出版社)
同课章节目录
