2021-2022学年高二上学期数学 人教A版(2019)选择性必修第一册2.5.2 圆与圆的位置关系 课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学 人教A版(2019)选择性必修第一册2.5.2 圆与圆的位置关系 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 911.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 20:58:13 | ||
图片预览






文档简介
(共28张PPT)
圆与圆的位置关系
1.理解圆与圆的位置关系的种类.
2.会根据两圆的圆心距与半径之间的关系判断出 两圆的位置关系.(重点)
3.会求两相交圆的公共弦方程、公共弦长度(难点)
消去y
判断直线和圆的位置关系的方法?
方法一:代数方法
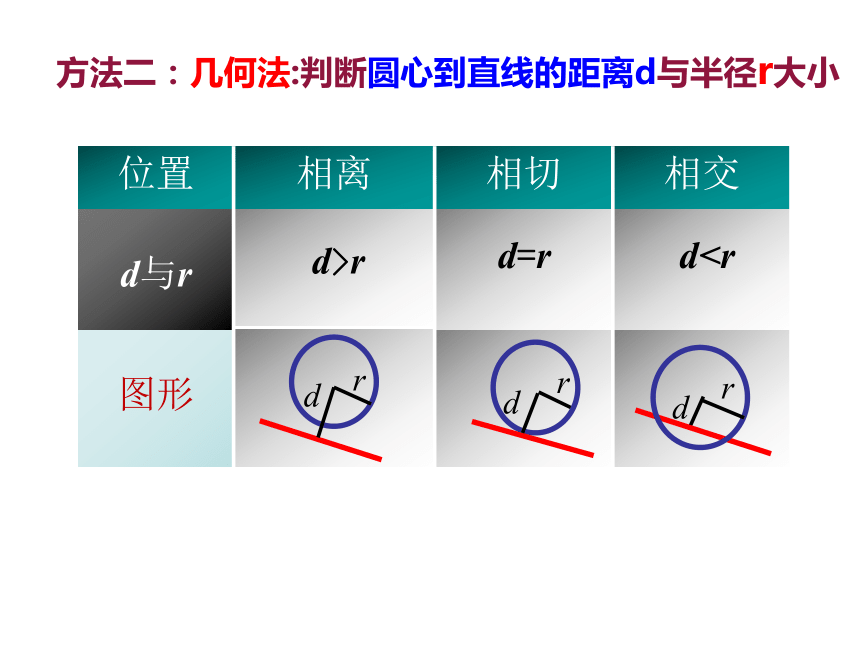
图形
d与r
相交
相切
相离
位置
dd=r
d>r
r
d
d
r
r
d
方法二:几何法:判断圆心到直线的距离d与半径r大小
思考1:
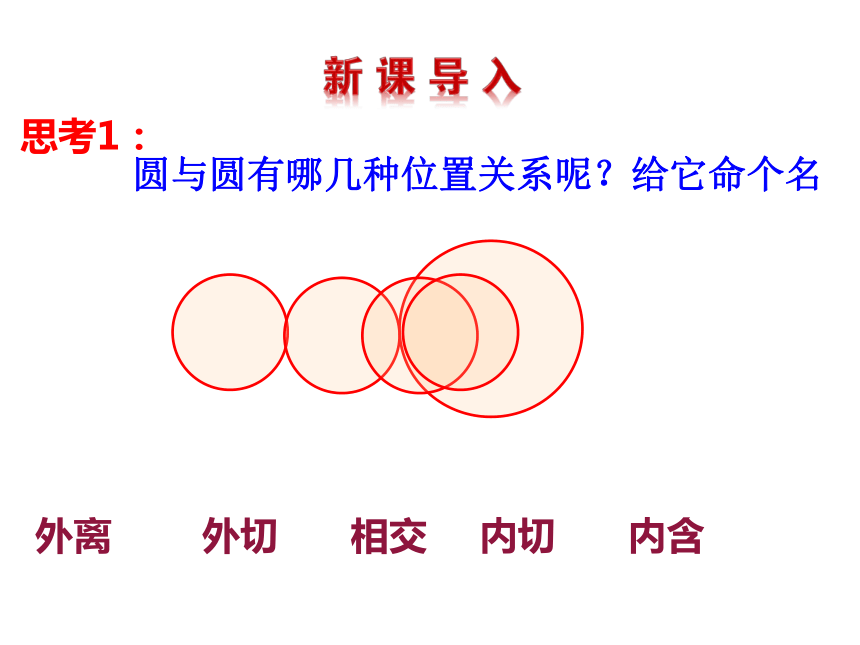
圆与圆有哪几种位置关系呢?给它命个名
外离
外切
相交
内切
内含
思考2:怎么判断圆与圆的位置关系?
1.相离(没有公共点)
2.相切(一个公共点)
3.相交(两个公共点)
外离
内含
内切
外切
代数法(消去x或者y,判断 的符号)
外离
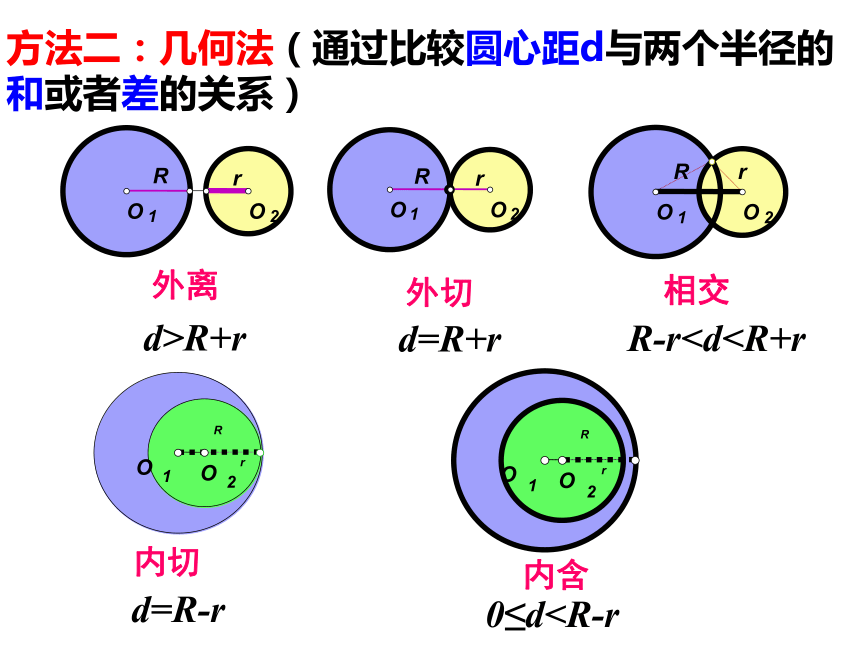
方法二:几何法(通过比较圆心距d与两个半径的和或者差的关系)
d>R+r
d=R+r
R-rd=R-r
0≤d外切
相交
内切
内含
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
1.利用代数方法判断
(1)当Δ=0时,有一个交点,两圆内切或外切,
(2)当Δ<0时,没有交点,两圆内含或相离,
消去其中的一个未知数y或x,得关于x或y的一元二次方程.
将两个圆方程联立,得
(3)当Δ>0时,有两个交点,两圆相交.
2.平面几何法判断圆与圆的位置关系公式
第一步:计算两圆的半径r1,r2;
第二步:计算两圆的圆心距d;
第三步:根据d与r1,r2之间的关系,判断两圆的位置关系.
两圆外离:r1+r2两圆外切:r1+r2=d;
两圆相交:|r1-r2|两圆内切:|r1-r2|=d;
两圆内含:|r1-r2|>d≥0.
例1、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
解法一(代数法):圆C1与圆C2的方程联立,得
(1)-(2),得
所以,方程(4)有两个不相等的实数根x1,x2,把x1,x2分别代入方程(3),得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).故两圆相交
解法二几何法:
把圆C1和圆C2的方程化为标准方程:
例1、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
所以圆C1与圆C2相交,它们有两个公共点A,B.
练习
1、已知圆C1 : x2+y2-10x-10y=0和 圆C2 : x2+y2+6x+2y-40=0试判断圆C1与圆C2的位置关系.
两种方法的优缺点:
几何方法直观,但不能求出交点;
代数方法能求出交点,但Δ=0,Δ<0 时,不能准确判断圆的位置关系.
【提升总结】
结论:单纯判断两圆位置关系时,常用几何法
探究2:
圆
与圆
相交于A,B两点,如何求公共弦的方程?
x
y
A
B
O
C1
C2
方法一:
将两圆方程联立,求出两个交点的坐标,利用两点式求公共弦的方程.
方法二:
先来探究一般情形.
已知圆
与圆
相交于A,B两点,
设
那么
同理可得
由③④可知
一定在直线
显然通过两点的直线只有一条,即直线方程唯一,
故公共弦的方程为
消去二次项
即两式相减
探究2:
圆
与圆
相交于A,B两点,如何求公共弦的方程?
两式相减即得到公共弦的方程为:-2x-1=0即得到:2x+1=0
例2:已知圆C1:x2+y2-10x-10y=0和圆C2:x2+y2+6x+2y-40=0相交于A、B 两点,求公共弦AB所在的直线方程,并求公共弦AB的长度.
解法一:由两圆的方程相减,消去二次项得到
一个二元一次方程,此方程为4x+3y=10.
即为公共弦AB 所在的直线方程,
由
解得
或
所以两点的坐标是A(-2,6),B(4,-2),或
A(4,-2),B(-2,6),
故|AB|=
则d=
解法二:先求出公共弦所在直线的方程:4x+3y-10=0.
x
y
A
B
O
C1
C2
.
d
R
把圆C1x2+y2-10x-10y=0的方程化为标准方程得到:
圆C1的圆心C1(5,5 ),半径R=
所以|AB|=
解:设两圆交点为A(x1,y1)、B(x2,y2),则A B两点坐标是方程组
①-②得3x-4y+6=0.
3x-4y+6=0即为两圆公共弦所在的直线方程.
易知圆C1的圆心(-1,3),半径r=3.
1.已知圆C1:x2+y2+2x-6y+1=0,圆C2:x2+y2-4x+2y-11=0.求两圆的公共弦所在的直线方程及公共弦长.
补充练习:
点M在圆心为C1的方程
上,
点N在圆心为C2的方程
上,
求|MN|的最大值。
1.圆与圆的位置关系及其判断方法(代数法、几何法)
2.学会求圆与圆相交时公共弦所在的直线方程(两式相减)及长度(弦长公式)。
不要贬低黄昏,黄昏同清晨一样是成就事业的时间。
圆与圆的位置关系
1.理解圆与圆的位置关系的种类.
2.会根据两圆的圆心距与半径之间的关系判断出 两圆的位置关系.(重点)
3.会求两相交圆的公共弦方程、公共弦长度(难点)
消去y
判断直线和圆的位置关系的方法?
方法一:代数方法
图形
d与r
相交
相切
相离
位置
d
d>r
r
d
d
r
r
d
方法二:几何法:判断圆心到直线的距离d与半径r大小
思考1:
圆与圆有哪几种位置关系呢?给它命个名
外离
外切
相交
内切
内含
思考2:怎么判断圆与圆的位置关系?
1.相离(没有公共点)
2.相切(一个公共点)
3.相交(两个公共点)
外离
内含
内切
外切
代数法(消去x或者y,判断 的符号)
外离
方法二:几何法(通过比较圆心距d与两个半径的和或者差的关系)
d>R+r
d=R+r
R-r
0≤d
相交
内切
内含
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
1.利用代数方法判断
(1)当Δ=0时,有一个交点,两圆内切或外切,
(2)当Δ<0时,没有交点,两圆内含或相离,
消去其中的一个未知数y或x,得关于x或y的一元二次方程.
将两个圆方程联立,得
(3)当Δ>0时,有两个交点,两圆相交.
2.平面几何法判断圆与圆的位置关系公式
第一步:计算两圆的半径r1,r2;
第二步:计算两圆的圆心距d;
第三步:根据d与r1,r2之间的关系,判断两圆的位置关系.
两圆外离:r1+r2
两圆相交:|r1-r2|
两圆内含:|r1-r2|>d≥0.
例1、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
解法一(代数法):圆C1与圆C2的方程联立,得
(1)-(2),得
所以,方程(4)有两个不相等的实数根x1,x2,把x1,x2分别代入方程(3),得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).故两圆相交
解法二几何法:
把圆C1和圆C2的方程化为标准方程:
例1、已知圆C1 : x2+y2+2x+8y-8=0和 圆C2 :x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
所以圆C1与圆C2相交,它们有两个公共点A,B.
练习
1、已知圆C1 : x2+y2-10x-10y=0和 圆C2 : x2+y2+6x+2y-40=0试判断圆C1与圆C2的位置关系.
两种方法的优缺点:
几何方法直观,但不能求出交点;
代数方法能求出交点,但Δ=0,Δ<0 时,不能准确判断圆的位置关系.
【提升总结】
结论:单纯判断两圆位置关系时,常用几何法
探究2:
圆
与圆
相交于A,B两点,如何求公共弦的方程?
x
y
A
B
O
C1
C2
方法一:
将两圆方程联立,求出两个交点的坐标,利用两点式求公共弦的方程.
方法二:
先来探究一般情形.
已知圆
与圆
相交于A,B两点,
设
那么
同理可得
由③④可知
一定在直线
显然通过两点的直线只有一条,即直线方程唯一,
故公共弦的方程为
消去二次项
即两式相减
探究2:
圆
与圆
相交于A,B两点,如何求公共弦的方程?
两式相减即得到公共弦的方程为:-2x-1=0即得到:2x+1=0
例2:已知圆C1:x2+y2-10x-10y=0和圆C2:x2+y2+6x+2y-40=0相交于A、B 两点,求公共弦AB所在的直线方程,并求公共弦AB的长度.
解法一:由两圆的方程相减,消去二次项得到
一个二元一次方程,此方程为4x+3y=10.
即为公共弦AB 所在的直线方程,
由
解得
或
所以两点的坐标是A(-2,6),B(4,-2),或
A(4,-2),B(-2,6),
故|AB|=
则d=
解法二:先求出公共弦所在直线的方程:4x+3y-10=0.
x
y
A
B
O
C1
C2
.
d
R
把圆C1x2+y2-10x-10y=0的方程化为标准方程得到:
圆C1的圆心C1(5,5 ),半径R=
所以|AB|=
解:设两圆交点为A(x1,y1)、B(x2,y2),则A B两点坐标是方程组
①-②得3x-4y+6=0.
3x-4y+6=0即为两圆公共弦所在的直线方程.
易知圆C1的圆心(-1,3),半径r=3.
1.已知圆C1:x2+y2+2x-6y+1=0,圆C2:x2+y2-4x+2y-11=0.求两圆的公共弦所在的直线方程及公共弦长.
补充练习:
点M在圆心为C1的方程
上,
点N在圆心为C2的方程
上,
求|MN|的最大值。
1.圆与圆的位置关系及其判断方法(代数法、几何法)
2.学会求圆与圆相交时公共弦所在的直线方程(两式相减)及长度(弦长公式)。
不要贬低黄昏,黄昏同清晨一样是成就事业的时间。
