【双减-同步分层作业】26.2 实际应用与反比例函数(含答案)
文档属性
| 名称 | 【双减-同步分层作业】26.2 实际应用与反比例函数(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 17:05:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【双减—同步分层作业】26.2实际问题与反比例函数
一、知识梳理
1、一定质量的氧气,它的密度是它的体积的反比例函数。当时,;当时,=________。
2、在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(4,3)在图象上,则当力达到10N时,物体在力的方向上移动的距离是___________m。
二、夯实基础(必做题)A
1、一司机驾驶汽车从甲地去乙地,他以80 km/h的平均速度用了4小时到达乙地,当他按原路匀速返回时,汽车的速度v(单位:km/h)与时间t(单位:h)的函数解析式是( )
A.v=320t B. C.v=20t D.
2、如图,在矩形ABCD中,AB=3,BC=4,点P在边BC上运动,连接DP,过点A作AE⊥DP,垂足为E。设DP=x,AE=y,则能反映y与x之间的函数的大致图象是( )
3、在温度不变的条件下,气体的压强和气体体积对应数值如下表,则可以反映y与x之间的关系的式子是( )
A. B. C. D.
4、码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间,轮船到达目的地后开始卸货,由于遇到紧急情况,需要将船上的货物不超过5天卸载完毕,那么平均每天至少要卸载货物的重量为( )
A.60吨 B.48吨 C.40吨 D.30吨
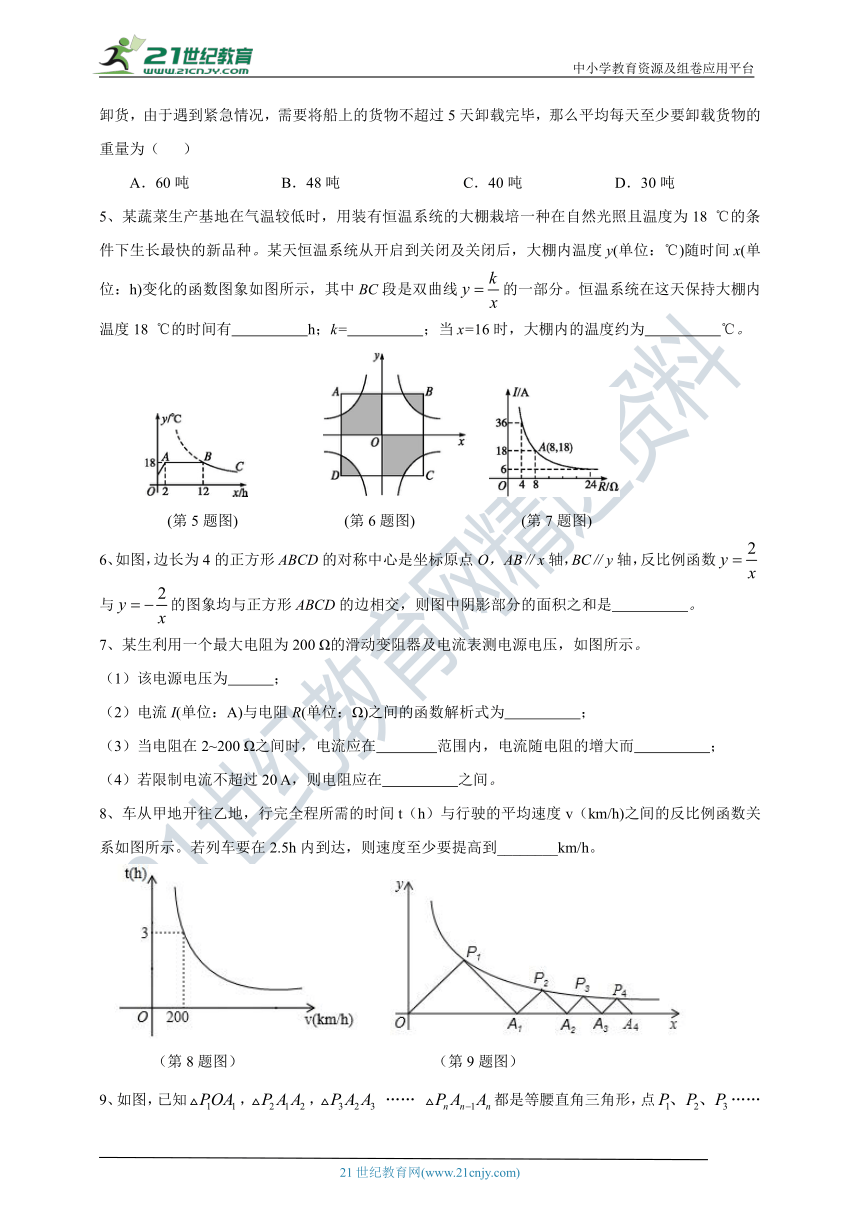
5、某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种。某天恒温系统从开启到关闭及关闭后,大棚内温度y(单位:℃)随时间x(单位:h)变化的函数图象如图所示,其中BC段是双曲线的一部分。恒温系统在这天保持大棚内温度18 ℃的时间有 h;k= ;当x=16时,大棚内的温度约为 ℃。
(第5题图) (第6题图) (第7题图)
6、如图,边长为4的正方形ABCD的对称中心是坐标原点O, AB∥x轴,BC∥y轴,反比例函数与的图象均与正方形ABCD的边相交,则图中阴影部分的面积之和是 。
7、某生利用一个最大电阻为200 Ω的滑动变阻器及电流表测电源电压,如图所示。
(1)该电源电压为 ;
(2)电流I(单位:A)与电阻R(单位:Ω)之间的函数解析式为 ;
(3)当电阻在2~200 Ω之间时,电流应在 范围内,电流随电阻的增大而 ;
(4)若限制电流不超过20 A,则电阻应在 之间。
8、车从甲地开往乙地,行完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的反比例函数关系如图所示。若列车要在2.5h内到达,则速度至少要提高到________km/h。
(第8题图) (第9题图)
9、如图,已知,, …… 都是等腰直角三角形,点……都在函数的图象上,斜边……都在x轴上,则点的坐标为_______________
10、某蓄水池的排水管每小时排水8 m3,6 h可将满池水全部排空。
(1)蓄水池的容积是多少
(2)如果增加排水管,使每小时的排水量达到Q(单位:m3),那么将满池水排空所需的时间t(单位:h)将如何变化
(3)写出t与Q的函数解析式。
(4)如果准备在5 h内将满池水排空,那么每小时的排水量至少为多少
(5)已知排水管的最大排水量为每小时12 m3,那么最少多长时间可将满池水全部排空
11、实验数据显示,一般成人喝250毫升低度白酒后,1.5时内其血液中酒精含量y(单位:毫克/百毫升)与时间x(单位:时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数(k>0)刻画(如图所示)。
(1)根据上述数学模型计算:
①喝酒后几小时后血液中的酒精含量达到最大值 最大值为多少
②当x=5时,y=45,求k的值。
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路。参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上7:00能否驾车去上班 请说明理由。
12、制作一种产品,需先将材料加热达到60 ℃后,再进行操作,设该材料温度为y(单位:℃),从加热开始计算的时间为x(单位:min)。据了解,该材料加热时,温度y与时间x成一次函数关系,停止加热进行操作时,温度y与时间x成反比例关系,如图,已知该材料在操作加工前的温度为15 ℃,加热5 min后的温度达到60 ℃。
(1)分别求出将材料加热和停止加热进行操作时,y关于x的函数解析式;
(2)根据工艺要求,如果当材料的温度低于15 ℃时,需停止操作,那么从开始加热到停止操作共经历了多长时间
13、某气球内充满了一定质量的气体,当温度不变时,气球内气体的压强p(单位:kPa)是气球体积V(单位:m3)的反比例函数,其图象如图所示(kPa是一种压强单位)。
(1)写出这个函数解析式。
(2)当气球的体积为0.8 m3时,气球内气体的压强是多少千帕
(3)当气球内气体的压强大于144 kPa时,气球将爆炸,为了安全起见,气球的体积不小于多少立方米
三、能力提升(中等生加练题)
1、如图是8个台阶的示意图,每个台阶的高和宽分别是2和3,每个台阶凸出的角的顶点记作(为1~8的整数),函数的图象为曲线L。
(1)若L过点,则=_______
(2)若L过点,则它必定还过另一点,则=________
(3)若曲线L使得~这些点分布在它的两侧,每侧各4个点,则的整数值有_______个。
2、某农户共摘收草莓1920千克,为寻求合适的销售价格,进行了6天试销,试销中发现这批草莓每天的销售量y(千克)与售价x(元/千克)之间成反比例关系。已知第1天以20元/千克的价格销售了45千克。现假定在这批草莓的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系。
(1)求y与x的函数关系式;
(2)在试销期间,第6天的销售价格比第2天低了9元/千克,但销售量却是第二天的2倍,求第二天的销售价格;
(3)试销6天共销售草莓420千克,该农户决定将草莓的售价定为15元/千克,并且每天都按这个价格销售,问余下的草莓预计还需多少天可以全部售完?
四、拓展训练(尖子生加练题)
1、小米利用暑期参加社会实践,在妈妈的帮助下,利用社区提供的免费摊点卖玩具。已知小米所有玩具的进价均2元/个。在销售过程中发现:每天玩具销售量y件与销售价格x元/件的关系如图所示,其中AB段为反比例函数图象的一部分,BC段为一次函数图象的一部分,设小米销售这种玩具的日利润为w元。
(1)根据图象,求出y与x之间的函数关系式;
(2)求出每天销售这种玩具的利润w(元)与x(元/件)之间的函数关系式,并求每天利润的最大值;
(3)若小米某天将价格定为超过4元(x>4),那么要使得小米在该天的销售利润不低于54元,求该天玩具销售价格的取值范围。
2、某厂从2017年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年 度 2017 2018 2019 2020
投入技改资金x/万元 2.5 3 4 4.5
产品成本y/(万元/件) 7.2 6 4.5 4
(1)请你认真分析表中数据,从你所学习过的一次函数、反比例函数中确定哪种函数能表示其变化规律,说明确定是这种函数而不是其他函数的理由,并求出它的解析式。
(2)按照这种变化规律,若2021年投入技改资金5万元。
①预计生产成本每件比2020年降低多少万元
②若打算在2021年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元 (结果精确到0.01万元)
【参考答案】
一、
1、0.68
2、1.2
二、
1、B
2、C
3、C
4、B
5、10 216 13.5
6、8 观察题图,看出阴影部分的面积是正方形ABCD的面积的一半。正方形ABCD的面积为16,所以阴影部分的面积之和为8。
7、(1)144 V (2) (3)0.72—72 A 减小 (4)7.2—200
8、240
9、
10、解:(1)蓄水池的容积是6×8=48m3
(2)增加排水管会使时间缩短,将满池水排空所需的时间t会减少
(3)因为容积V=48m3,所以解析式为
(4),Q≥9.6(m3),即每小时的排水量至少为9.6m3
(5)设最少用xh将满池水排空,根据题意,得12x≥48,解得x≥4,即最少用4h可将满池水全部排空。
11、解:(1)①y=-200x2+400x=-200(x-1)2+200,
∴喝酒后1时后血液中的酒精含量达到最大值,最大值为200毫克/百毫升。
②∵当x=5时,y=45,
∴k=xy=45×5=225。
(2)不能驾车上班。
理由:∵晚上20:00到第二天早上7:00,一共有11小时,
∴将x=11代入,则
∴第二天早上7:00不能驾车去上班。
12、解:(1)设材料加热时,y关于x的一次函数解析式为y=k1x+b(k1≠0),
由题意知,当x=0时,y=15;当x=5时,y=60。
代入y=k1x+b,得
解得
所以y=9x+15,x的取值范围是0≤x≤5。
设停止加热进行操作时,y关于x的函数解析式为(k2≠0),
由题意,当x=5时,y=60,代入函数解析式,得。所以k2=300,即进行操作时y与x的函数解析式为(x≥5)。
(2)由题意知,当y=15时,
由,得。
所以x=20,即当x=20min时,材料温度为15℃,由反比例函数的性质,当x>20时,y<15,即从开始加热到停止操作共经历了20min。
13、解:(1)根据题意,设(k≠0)。
∵A(1.5,64)是其图象上的一点,将A(1.5,64)代入,得,解得k=96,
即p与V之间的函数解析式为(V>0)
(2)当V=0.8m3时,=120(kPa)
∴气球内气体的压强是120kPA.
(3)∵当气球内气体的压强大于144kPa时,气球将爆炸,∴p≤144,即≤144。
∴V≥m3。
∴为了安全起见,气球的体积不小于m3。
三、
1、(1)∵每个台阶的高和宽分别是2和3,
∴T1(24,2),T2(21,4),T3(18,6),T4(15,8),T5(12,10),T6(9,12),T7(6,14),T8(3,16),
∵L过点T1,
∴k=24×2=48,
故答案为:48;
(2)∵L过点T4,
∴k=15×8=120,
∴反比例函数解析式为:y=,
当x=12时,y=10,
∴T5在反比例函数图象上,
∴m=5,
故答案为:5;
(3)若曲线L过点T1(24,2),T8(3,16)时,k=48,
若曲线L过点T2(21,4),T7(6,14)时,k=84,
若曲线L过点T3(18,6),T6(9,12)时,k=108,
若曲线L过点T4(15,8),T5(12,10)时,k=120,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点
∴84<k<108
∴整数k共有:108-(84+1)=23(个)
故答案为:23
2、解:(1)设函数关系式为,把代入,得
解得
∴函数关系式为
(2)设第二天的销售价格为元,由题意得
解得
经检验,是元分式方程的解。
∴第二天的销售价格是18元/千克。
(3)当草莓的售价定为15元/千克时,每天的销售量为千克
天数:天
∴余下的草莓预计还要销售25天。
四、
1、解:(1)∵AB段为反比例函数图象的一部分,A(2,40),B(4,20)
∴当时,
∵BC段为一次函数图象的一部分,B(4,20),C(14,0)
∴设BC段的函数关系式为y=kx+b,把B(4,20),C(14,0)代入,得
解得
∴当时,y=-2x+28
∴y与x之间的函数关系式为
(2)当时,
∵随着x的增大,逐渐增大,也逐渐增大
∴当x=4时,w取得最大值为40
当时,
∵且
∴当x=8时,w取得最大值为72
综上所述,每天利润的最大值为72元。
(3)由题意可知:
令,即
解得
由函数表达式及函数图象可知,要使,则
∴当时,小米的销售利润不低于54元。
2、解:(1)若为一次函数,设其解析式为y=k1x+b(k1≠0),
因为当x=2.5时,y=7.2;当x=3时,y=6,
所以
解得
所以一次函数的解析式为y=-2.4x+13.2
把x=4时,y=4.5代入此函数解析式得,左边≠右边。故不是一次函数。若为反比例函数,设其解析式为(k2≠0),当x=2.5时,y=7.2,可得,得k2=18。所以反比例函数解析式为
验证:当x=3时,,符合反比例函数。
同理可验证:当x=4时,y=4.5;当x=4.5时,y=4成立。故可用反比例函数表示其变化规律。
(2)①当x=5时,
因为4-3.6=0.4(万元),
所以预计生产成本每件比2020年降低0.4万元。
②当y=3.2时,,得x=5.625
因为5.625-5=0.625≈0.63(万元)
所以还需投入技改资金约0.63万元。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【双减—同步分层作业】26.2实际问题与反比例函数
一、知识梳理
1、一定质量的氧气,它的密度是它的体积的反比例函数。当时,;当时,=________。
2、在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(4,3)在图象上,则当力达到10N时,物体在力的方向上移动的距离是___________m。
二、夯实基础(必做题)A
1、一司机驾驶汽车从甲地去乙地,他以80 km/h的平均速度用了4小时到达乙地,当他按原路匀速返回时,汽车的速度v(单位:km/h)与时间t(单位:h)的函数解析式是( )
A.v=320t B. C.v=20t D.
2、如图,在矩形ABCD中,AB=3,BC=4,点P在边BC上运动,连接DP,过点A作AE⊥DP,垂足为E。设DP=x,AE=y,则能反映y与x之间的函数的大致图象是( )
3、在温度不变的条件下,气体的压强和气体体积对应数值如下表,则可以反映y与x之间的关系的式子是( )
A. B. C. D.
4、码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间,轮船到达目的地后开始卸货,由于遇到紧急情况,需要将船上的货物不超过5天卸载完毕,那么平均每天至少要卸载货物的重量为( )
A.60吨 B.48吨 C.40吨 D.30吨
5、某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种。某天恒温系统从开启到关闭及关闭后,大棚内温度y(单位:℃)随时间x(单位:h)变化的函数图象如图所示,其中BC段是双曲线的一部分。恒温系统在这天保持大棚内温度18 ℃的时间有 h;k= ;当x=16时,大棚内的温度约为 ℃。
(第5题图) (第6题图) (第7题图)
6、如图,边长为4的正方形ABCD的对称中心是坐标原点O, AB∥x轴,BC∥y轴,反比例函数与的图象均与正方形ABCD的边相交,则图中阴影部分的面积之和是 。
7、某生利用一个最大电阻为200 Ω的滑动变阻器及电流表测电源电压,如图所示。
(1)该电源电压为 ;
(2)电流I(单位:A)与电阻R(单位:Ω)之间的函数解析式为 ;
(3)当电阻在2~200 Ω之间时,电流应在 范围内,电流随电阻的增大而 ;
(4)若限制电流不超过20 A,则电阻应在 之间。
8、车从甲地开往乙地,行完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的反比例函数关系如图所示。若列车要在2.5h内到达,则速度至少要提高到________km/h。
(第8题图) (第9题图)
9、如图,已知,, …… 都是等腰直角三角形,点……都在函数的图象上,斜边……都在x轴上,则点的坐标为_______________
10、某蓄水池的排水管每小时排水8 m3,6 h可将满池水全部排空。
(1)蓄水池的容积是多少
(2)如果增加排水管,使每小时的排水量达到Q(单位:m3),那么将满池水排空所需的时间t(单位:h)将如何变化
(3)写出t与Q的函数解析式。
(4)如果准备在5 h内将满池水排空,那么每小时的排水量至少为多少
(5)已知排水管的最大排水量为每小时12 m3,那么最少多长时间可将满池水全部排空
11、实验数据显示,一般成人喝250毫升低度白酒后,1.5时内其血液中酒精含量y(单位:毫克/百毫升)与时间x(单位:时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数(k>0)刻画(如图所示)。
(1)根据上述数学模型计算:
①喝酒后几小时后血液中的酒精含量达到最大值 最大值为多少
②当x=5时,y=45,求k的值。
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路。参照上述数学模型,假设某驾驶员晚上20:00在家喝完250毫升低度白酒,第二天早上7:00能否驾车去上班 请说明理由。
12、制作一种产品,需先将材料加热达到60 ℃后,再进行操作,设该材料温度为y(单位:℃),从加热开始计算的时间为x(单位:min)。据了解,该材料加热时,温度y与时间x成一次函数关系,停止加热进行操作时,温度y与时间x成反比例关系,如图,已知该材料在操作加工前的温度为15 ℃,加热5 min后的温度达到60 ℃。
(1)分别求出将材料加热和停止加热进行操作时,y关于x的函数解析式;
(2)根据工艺要求,如果当材料的温度低于15 ℃时,需停止操作,那么从开始加热到停止操作共经历了多长时间
13、某气球内充满了一定质量的气体,当温度不变时,气球内气体的压强p(单位:kPa)是气球体积V(单位:m3)的反比例函数,其图象如图所示(kPa是一种压强单位)。
(1)写出这个函数解析式。
(2)当气球的体积为0.8 m3时,气球内气体的压强是多少千帕
(3)当气球内气体的压强大于144 kPa时,气球将爆炸,为了安全起见,气球的体积不小于多少立方米
三、能力提升(中等生加练题)
1、如图是8个台阶的示意图,每个台阶的高和宽分别是2和3,每个台阶凸出的角的顶点记作(为1~8的整数),函数的图象为曲线L。
(1)若L过点,则=_______
(2)若L过点,则它必定还过另一点,则=________
(3)若曲线L使得~这些点分布在它的两侧,每侧各4个点,则的整数值有_______个。
2、某农户共摘收草莓1920千克,为寻求合适的销售价格,进行了6天试销,试销中发现这批草莓每天的销售量y(千克)与售价x(元/千克)之间成反比例关系。已知第1天以20元/千克的价格销售了45千克。现假定在这批草莓的销售中,每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系。
(1)求y与x的函数关系式;
(2)在试销期间,第6天的销售价格比第2天低了9元/千克,但销售量却是第二天的2倍,求第二天的销售价格;
(3)试销6天共销售草莓420千克,该农户决定将草莓的售价定为15元/千克,并且每天都按这个价格销售,问余下的草莓预计还需多少天可以全部售完?
四、拓展训练(尖子生加练题)
1、小米利用暑期参加社会实践,在妈妈的帮助下,利用社区提供的免费摊点卖玩具。已知小米所有玩具的进价均2元/个。在销售过程中发现:每天玩具销售量y件与销售价格x元/件的关系如图所示,其中AB段为反比例函数图象的一部分,BC段为一次函数图象的一部分,设小米销售这种玩具的日利润为w元。
(1)根据图象,求出y与x之间的函数关系式;
(2)求出每天销售这种玩具的利润w(元)与x(元/件)之间的函数关系式,并求每天利润的最大值;
(3)若小米某天将价格定为超过4元(x>4),那么要使得小米在该天的销售利润不低于54元,求该天玩具销售价格的取值范围。
2、某厂从2017年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年 度 2017 2018 2019 2020
投入技改资金x/万元 2.5 3 4 4.5
产品成本y/(万元/件) 7.2 6 4.5 4
(1)请你认真分析表中数据,从你所学习过的一次函数、反比例函数中确定哪种函数能表示其变化规律,说明确定是这种函数而不是其他函数的理由,并求出它的解析式。
(2)按照这种变化规律,若2021年投入技改资金5万元。
①预计生产成本每件比2020年降低多少万元
②若打算在2021年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元 (结果精确到0.01万元)
【参考答案】
一、
1、0.68
2、1.2
二、
1、B
2、C
3、C
4、B
5、10 216 13.5
6、8 观察题图,看出阴影部分的面积是正方形ABCD的面积的一半。正方形ABCD的面积为16,所以阴影部分的面积之和为8。
7、(1)144 V (2) (3)0.72—72 A 减小 (4)7.2—200
8、240
9、
10、解:(1)蓄水池的容积是6×8=48m3
(2)增加排水管会使时间缩短,将满池水排空所需的时间t会减少
(3)因为容积V=48m3,所以解析式为
(4),Q≥9.6(m3),即每小时的排水量至少为9.6m3
(5)设最少用xh将满池水排空,根据题意,得12x≥48,解得x≥4,即最少用4h可将满池水全部排空。
11、解:(1)①y=-200x2+400x=-200(x-1)2+200,
∴喝酒后1时后血液中的酒精含量达到最大值,最大值为200毫克/百毫升。
②∵当x=5时,y=45,
∴k=xy=45×5=225。
(2)不能驾车上班。
理由:∵晚上20:00到第二天早上7:00,一共有11小时,
∴将x=11代入,则
∴第二天早上7:00不能驾车去上班。
12、解:(1)设材料加热时,y关于x的一次函数解析式为y=k1x+b(k1≠0),
由题意知,当x=0时,y=15;当x=5时,y=60。
代入y=k1x+b,得
解得
所以y=9x+15,x的取值范围是0≤x≤5。
设停止加热进行操作时,y关于x的函数解析式为(k2≠0),
由题意,当x=5时,y=60,代入函数解析式,得。所以k2=300,即进行操作时y与x的函数解析式为(x≥5)。
(2)由题意知,当y=15时,
由,得。
所以x=20,即当x=20min时,材料温度为15℃,由反比例函数的性质,当x>20时,y<15,即从开始加热到停止操作共经历了20min。
13、解:(1)根据题意,设(k≠0)。
∵A(1.5,64)是其图象上的一点,将A(1.5,64)代入,得,解得k=96,
即p与V之间的函数解析式为(V>0)
(2)当V=0.8m3时,=120(kPa)
∴气球内气体的压强是120kPA.
(3)∵当气球内气体的压强大于144kPa时,气球将爆炸,∴p≤144,即≤144。
∴V≥m3。
∴为了安全起见,气球的体积不小于m3。
三、
1、(1)∵每个台阶的高和宽分别是2和3,
∴T1(24,2),T2(21,4),T3(18,6),T4(15,8),T5(12,10),T6(9,12),T7(6,14),T8(3,16),
∵L过点T1,
∴k=24×2=48,
故答案为:48;
(2)∵L过点T4,
∴k=15×8=120,
∴反比例函数解析式为:y=,
当x=12时,y=10,
∴T5在反比例函数图象上,
∴m=5,
故答案为:5;
(3)若曲线L过点T1(24,2),T8(3,16)时,k=48,
若曲线L过点T2(21,4),T7(6,14)时,k=84,
若曲线L过点T3(18,6),T6(9,12)时,k=108,
若曲线L过点T4(15,8),T5(12,10)时,k=120,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点
∴84<k<108
∴整数k共有:108-(84+1)=23(个)
故答案为:23
2、解:(1)设函数关系式为,把代入,得
解得
∴函数关系式为
(2)设第二天的销售价格为元,由题意得
解得
经检验,是元分式方程的解。
∴第二天的销售价格是18元/千克。
(3)当草莓的售价定为15元/千克时,每天的销售量为千克
天数:天
∴余下的草莓预计还要销售25天。
四、
1、解:(1)∵AB段为反比例函数图象的一部分,A(2,40),B(4,20)
∴当时,
∵BC段为一次函数图象的一部分,B(4,20),C(14,0)
∴设BC段的函数关系式为y=kx+b,把B(4,20),C(14,0)代入,得
解得
∴当时,y=-2x+28
∴y与x之间的函数关系式为
(2)当时,
∵随着x的增大,逐渐增大,也逐渐增大
∴当x=4时,w取得最大值为40
当时,
∵且
∴当x=8时,w取得最大值为72
综上所述,每天利润的最大值为72元。
(3)由题意可知:
令,即
解得
由函数表达式及函数图象可知,要使,则
∴当时,小米的销售利润不低于54元。
2、解:(1)若为一次函数,设其解析式为y=k1x+b(k1≠0),
因为当x=2.5时,y=7.2;当x=3时,y=6,
所以
解得
所以一次函数的解析式为y=-2.4x+13.2
把x=4时,y=4.5代入此函数解析式得,左边≠右边。故不是一次函数。若为反比例函数,设其解析式为(k2≠0),当x=2.5时,y=7.2,可得,得k2=18。所以反比例函数解析式为
验证:当x=3时,,符合反比例函数。
同理可验证:当x=4时,y=4.5;当x=4.5时,y=4成立。故可用反比例函数表示其变化规律。
(2)①当x=5时,
因为4-3.6=0.4(万元),
所以预计生产成本每件比2020年降低0.4万元。
②当y=3.2时,,得x=5.625
因为5.625-5=0.625≈0.63(万元)
所以还需投入技改资金约0.63万元。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
