沪科版数学七年级上册 第1章 有理数 教案
文档属性
| 名称 | 沪科版数学七年级上册 第1章 有理数 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 42.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览


文档简介
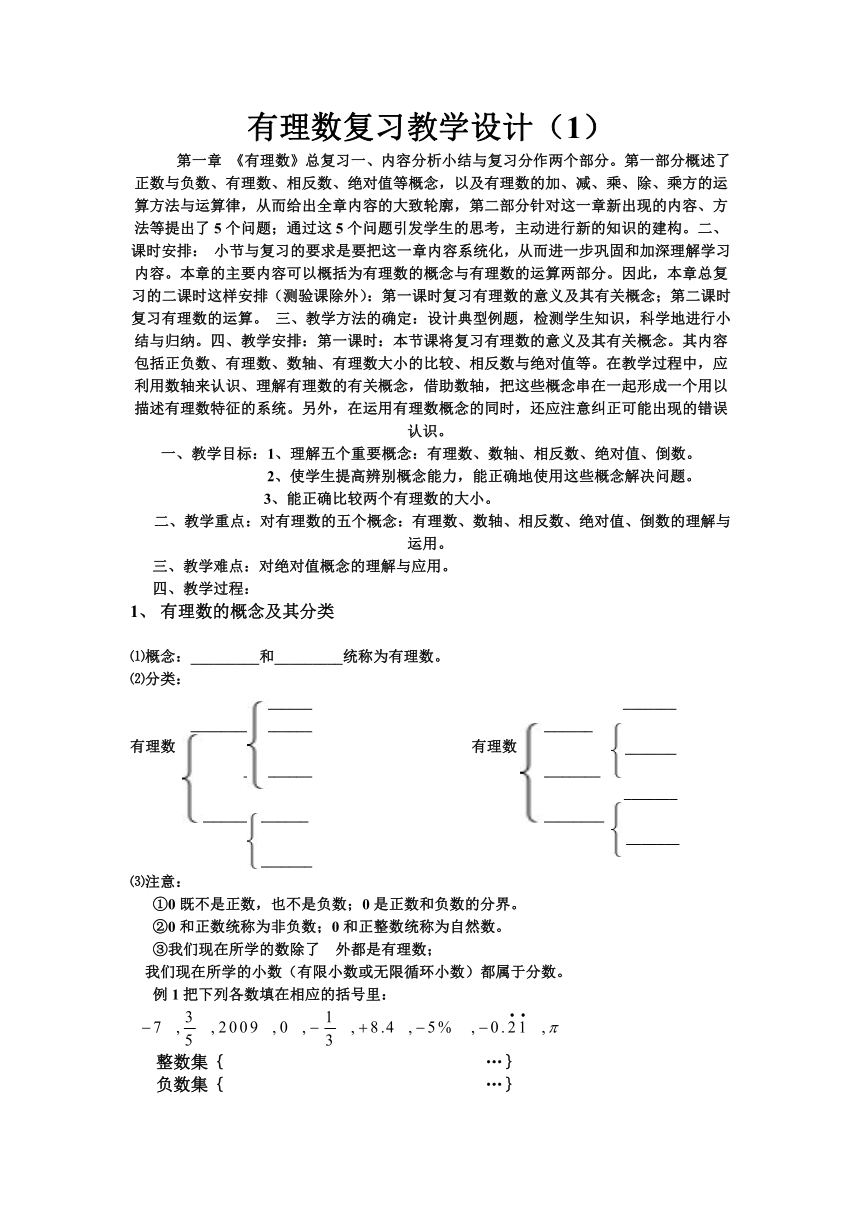
有理数复习教学设计(1)
第一章 《有理数》总复习一、内容分析小结与复习分作两个部分。第一部分概述了正数与负数、有理数、相反数、绝对值等概念,以及有理数的加、减、乘、除、乘方的运算方法与运算律,从而给出全章内容的大致轮廓,第二部分针对这一章新出现的内容、方法等提出了5个问题;通过这5个问题引发学生的思考,主动进行新的知识的建构。二、课时安排: 小节与复习的要求是要把这一章内容系统化,从而进一步巩固和加深理解学习内容。本章的主要内容可以概括为有理数的概念与有理数的运算两部分。因此,本章总复习的二课时这样安排(测验课除外):第一课时复习有理数的意义及其有关概念;第二课时复习有理数的运算。 三、教学方法的确定:设计典型例题,检测学生知识,科学地进行小结与归纳。四、教学安排:第一课时:本节课将复习有理数的意义及其有关概念。其内容包括正负数、有理数、数轴、有理数大小的比较、相反数与绝对值等。在教学过程中,应利用数轴来认识、理解有理数的有关概念,借助数轴,把这些概念串在一起形成一个用以描述有理数特征的系统。另外,在运用有理数概念的同时,还应注意纠正可能出现的错误认识。
一、教学目标:1、理解五个重要概念:有理数、数轴、相反数、绝对值、倒数。
2、使学生提高辨别概念能力,能正确地使用这些概念解决问题。
3、能正确比较两个有理数的大小。
二、教学重点:对有理数的五个概念:有理数、数轴、相反数、绝对值、倒数的理解与运用。
三、教学难点:对绝对值概念的理解与应用。
四、教学过程:
有理数的概念及其分类
⑴概念:_________和_________统称为有理数。
⑵分类:
_______ _______
________ ______ ________
有理数 有理数 _______
_ ______ ________
_______
_______ _______ ________
_______
_______
⑶注意:
①0既不是正数,也不是负数;0是正数和负数的分界。
②0和正数统称为非负数;0和正整数统称为自然数。
③我们现在所学的数除了 外都是有理数;
我们现在所学的小数(有限小数或无限循环小数)都属于分数。
例1把下列各数填在相应的括号里:
整数集{ …}
负数集{ …}
非负整数集{ …}
负分数集{ …}
有理数集{ …}
⑷正数和负数的意义:
表示现实生活中的______________的两个量
例2 某升降机上升了4m,表示为+4m,那么下降了3m,应记作_______ 。
若规定收入为“+”,则支出-50元表示______________。
2、数轴
⑴概念:规定了_______、_______、_______的直线叫做数轴。
⑵应用:
①任何一个有理数都可以用数轴上的点来表示。
②比较大小:数轴上两个点表示的数,右边的数总比左边数的大。
例3 画出数轴,把下列各数在数轴上表示出来,并按从小到大的顺序,用“<”连接起来
解:
最大的负整数是 _______,最小的正整数是_______。
3、相反数
⑴概念:只有____________的两个数称为互为相反数。
0的相反数是0。a的相反数是_______。
倒数:乘积是_____的两个数互为倒数。
0没有倒数。a的倒数是______。
⑵几何意义:互为相反数的两个数在数轴上的对应点(0除外),位于_______两旁,且与_______的距离相等,即关于_______对称。
⑶符号法则:同号得正,异号得负。
⑷若a和b是互为相反数,则a + b =0,(b0)
例4 的相反数是_______,倒数是 _______。
例5 化简:
-(+8)=_______ , +(-9)=_______ , -(-6)=_______, +(+5)=_______ 。
4、绝对值
⑴概念:在数轴上表示数a的点与_________________叫做数a的绝对值。
⑵求法:
|a|=
⑶性质:①任何一个有理数的绝对值是非负数,即|a|≥0
例6 若 +(6+3)=0,则a=______, b=______。
②互为相反数的两个数绝对值相等。
例7 若|x|=16,则x = ____。
例8 绝对值不大于3的整数有 __个,分别是_________________。
⑷应用:
|a – b|表示数轴上数a、b两点间的距离
例9 在数轴上与表示-1的点相距4个单位长度的点表示的数是_________。
5、有理数比较大小
⑴利用数轴: 数轴上两个点表示的数,右边的数总比左边数的大。
⑵有理数比较法则:
正数大于0,负数小于0,正数大于负数;两个负数,绝对值大的反而小。
例10 比较大小: (用“>”、“<”或“=”填空)
-3.3 _____ 0 , 6____ -8 , 0 _____2,
6、科学记数法
:⑴a整数位只有一位,即1≤a<10。
⑵正整数n=原数整数数位 1。
例11 用科学记数法表示下列各数:
⑴696000; ⑵354.87; ⑶640万。
解:
例12 数的原数是 _______________。
准确数与近似数
⑴概念: ⒈准确数——与实际完全符合的数;
⒉近似数——与实际接近的数
例如:下列各选项中的数字是准确数的是( )
A 这本书约有20万字 B 某班学生有54人
C 我市共有200万人口 D 我国的国土面积为960万平方千米
⑵精确度:
①四舍五入到哪一位就说精确到哪一位;
②有效数字(由四舍五入得到的近似数,从左边第一个不是0的数起,到精确到的那一位数位止,所有的数字都叫做这个数的有效数字);
例13 下列有四舍五入法得到的近似数,各精确到哪 一位?
⑴132.4;⑵0.0572;⑶2.50万;⑷6.4× 10
解:
例14 用四舍五入法,按括号中的要求把下列各数取近似数:
⑴0.34082(精确到千分位); ⑵54.973(精确到0.1);
⑶2674.28万(精确到千位);⑷30542(精确到百位)。
解:
三课堂小结:要注意的几个问题(1)有理数的两种分类经常用到,应注意它们的区别;(2)数轴的三要素缺一不可,利用数轴可直观地比较有理数的大小;(3)相反数指的是两个仅符号不同的数,数轴上表示一对相反数的两个点到原点的距离相等,它们的和为0;而倒数指的是两个乘积为1的数;(4)一个数的绝对值总是非负数,数a的绝对值是数轴上表示数a的点到原点的距离;
达标检测.
1、数轴的单位长度为1,如果A、B表示的数的绝对值相等,那么A表示的数是( )
(
A
B
)
A —4 B —2 C 0 D 4
2 、 若 a+2的相反数是1,则a的倒数是_____
3、 若+=0, 则 —1=______
4、有理数a、b在数轴上对应点如图所示,
(
b
-1
1
a
0
)
将a、—a、b、—1、1 用“<”号排列出来。
5 、 有理数满足=5 =11 求a+b的值
6.若a、b互为相反数,c、d互为倒数,=4 求2a—(cd) +2b—3m的值.
第一章 《有理数》总复习一、内容分析小结与复习分作两个部分。第一部分概述了正数与负数、有理数、相反数、绝对值等概念,以及有理数的加、减、乘、除、乘方的运算方法与运算律,从而给出全章内容的大致轮廓,第二部分针对这一章新出现的内容、方法等提出了5个问题;通过这5个问题引发学生的思考,主动进行新的知识的建构。二、课时安排: 小节与复习的要求是要把这一章内容系统化,从而进一步巩固和加深理解学习内容。本章的主要内容可以概括为有理数的概念与有理数的运算两部分。因此,本章总复习的二课时这样安排(测验课除外):第一课时复习有理数的意义及其有关概念;第二课时复习有理数的运算。 三、教学方法的确定:设计典型例题,检测学生知识,科学地进行小结与归纳。四、教学安排:第一课时:本节课将复习有理数的意义及其有关概念。其内容包括正负数、有理数、数轴、有理数大小的比较、相反数与绝对值等。在教学过程中,应利用数轴来认识、理解有理数的有关概念,借助数轴,把这些概念串在一起形成一个用以描述有理数特征的系统。另外,在运用有理数概念的同时,还应注意纠正可能出现的错误认识。
一、教学目标:1、理解五个重要概念:有理数、数轴、相反数、绝对值、倒数。
2、使学生提高辨别概念能力,能正确地使用这些概念解决问题。
3、能正确比较两个有理数的大小。
二、教学重点:对有理数的五个概念:有理数、数轴、相反数、绝对值、倒数的理解与运用。
三、教学难点:对绝对值概念的理解与应用。
四、教学过程:
有理数的概念及其分类
⑴概念:_________和_________统称为有理数。
⑵分类:
_______ _______
________ ______ ________
有理数 有理数 _______
_ ______ ________
_______
_______ _______ ________
_______
_______
⑶注意:
①0既不是正数,也不是负数;0是正数和负数的分界。
②0和正数统称为非负数;0和正整数统称为自然数。
③我们现在所学的数除了 外都是有理数;
我们现在所学的小数(有限小数或无限循环小数)都属于分数。
例1把下列各数填在相应的括号里:
整数集{ …}
负数集{ …}
非负整数集{ …}
负分数集{ …}
有理数集{ …}
⑷正数和负数的意义:
表示现实生活中的______________的两个量
例2 某升降机上升了4m,表示为+4m,那么下降了3m,应记作_______ 。
若规定收入为“+”,则支出-50元表示______________。
2、数轴
⑴概念:规定了_______、_______、_______的直线叫做数轴。
⑵应用:
①任何一个有理数都可以用数轴上的点来表示。
②比较大小:数轴上两个点表示的数,右边的数总比左边数的大。
例3 画出数轴,把下列各数在数轴上表示出来,并按从小到大的顺序,用“<”连接起来
解:
最大的负整数是 _______,最小的正整数是_______。
3、相反数
⑴概念:只有____________的两个数称为互为相反数。
0的相反数是0。a的相反数是_______。
倒数:乘积是_____的两个数互为倒数。
0没有倒数。a的倒数是______。
⑵几何意义:互为相反数的两个数在数轴上的对应点(0除外),位于_______两旁,且与_______的距离相等,即关于_______对称。
⑶符号法则:同号得正,异号得负。
⑷若a和b是互为相反数,则a + b =0,(b0)
例4 的相反数是_______,倒数是 _______。
例5 化简:
-(+8)=_______ , +(-9)=_______ , -(-6)=_______, +(+5)=_______ 。
4、绝对值
⑴概念:在数轴上表示数a的点与_________________叫做数a的绝对值。
⑵求法:
|a|=
⑶性质:①任何一个有理数的绝对值是非负数,即|a|≥0
例6 若 +(6+3)=0,则a=______, b=______。
②互为相反数的两个数绝对值相等。
例7 若|x|=16,则x = ____。
例8 绝对值不大于3的整数有 __个,分别是_________________。
⑷应用:
|a – b|表示数轴上数a、b两点间的距离
例9 在数轴上与表示-1的点相距4个单位长度的点表示的数是_________。
5、有理数比较大小
⑴利用数轴: 数轴上两个点表示的数,右边的数总比左边数的大。
⑵有理数比较法则:
正数大于0,负数小于0,正数大于负数;两个负数,绝对值大的反而小。
例10 比较大小: (用“>”、“<”或“=”填空)
-3.3 _____ 0 , 6____ -8 , 0 _____2,
6、科学记数法
:⑴a整数位只有一位,即1≤a<10。
⑵正整数n=原数整数数位 1。
例11 用科学记数法表示下列各数:
⑴696000; ⑵354.87; ⑶640万。
解:
例12 数的原数是 _______________。
准确数与近似数
⑴概念: ⒈准确数——与实际完全符合的数;
⒉近似数——与实际接近的数
例如:下列各选项中的数字是准确数的是( )
A 这本书约有20万字 B 某班学生有54人
C 我市共有200万人口 D 我国的国土面积为960万平方千米
⑵精确度:
①四舍五入到哪一位就说精确到哪一位;
②有效数字(由四舍五入得到的近似数,从左边第一个不是0的数起,到精确到的那一位数位止,所有的数字都叫做这个数的有效数字);
例13 下列有四舍五入法得到的近似数,各精确到哪 一位?
⑴132.4;⑵0.0572;⑶2.50万;⑷6.4× 10
解:
例14 用四舍五入法,按括号中的要求把下列各数取近似数:
⑴0.34082(精确到千分位); ⑵54.973(精确到0.1);
⑶2674.28万(精确到千位);⑷30542(精确到百位)。
解:
三课堂小结:要注意的几个问题(1)有理数的两种分类经常用到,应注意它们的区别;(2)数轴的三要素缺一不可,利用数轴可直观地比较有理数的大小;(3)相反数指的是两个仅符号不同的数,数轴上表示一对相反数的两个点到原点的距离相等,它们的和为0;而倒数指的是两个乘积为1的数;(4)一个数的绝对值总是非负数,数a的绝对值是数轴上表示数a的点到原点的距离;
达标检测.
1、数轴的单位长度为1,如果A、B表示的数的绝对值相等,那么A表示的数是( )
(
A
B
)
A —4 B —2 C 0 D 4
2 、 若 a+2的相反数是1,则a的倒数是_____
3、 若+=0, 则 —1=______
4、有理数a、b在数轴上对应点如图所示,
(
b
-1
1
a
0
)
将a、—a、b、—1、1 用“<”号排列出来。
5 、 有理数满足=5 =11 求a+b的值
6.若a、b互为相反数,c、d互为倒数,=4 求2a—(cd) +2b—3m的值.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
