鲁教版(五四制)数学六年级上册 1.2 展开与折叠-第二课时课件(共18张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学六年级上册 1.2 展开与折叠-第二课时课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 291.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第二课时
展开与折叠
教学目标:
1.经历图形的展开与折叠的活动,发展空间观念,积累数学活动经验。
2.认识正方体、圆柱、圆锥、棱柱的侧面展开图,能根据展开图判断能否折成几何体。
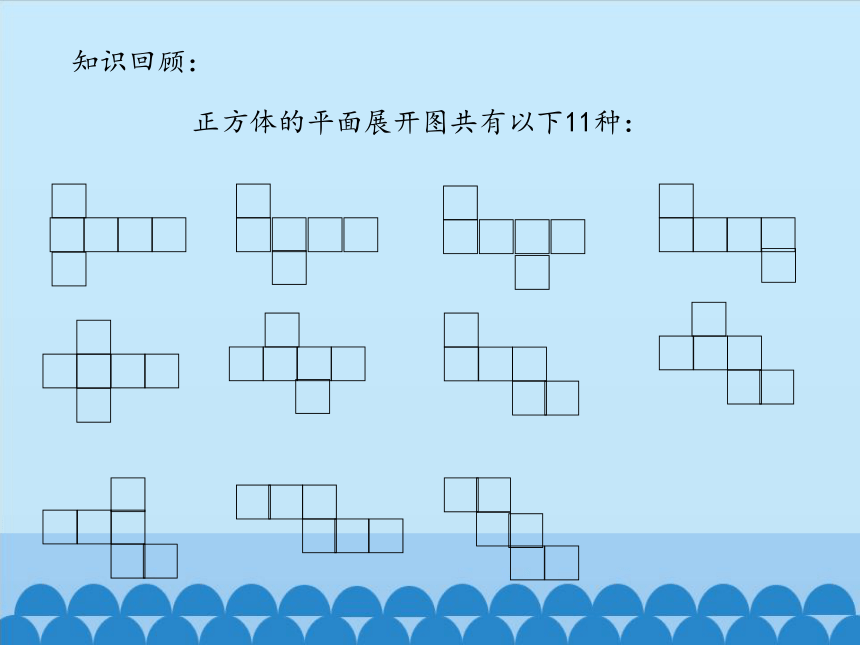
正方体的平面展开图共有以下11种:
知识回顾:
正方体的表面展开图“口诀”:
一线不过四,
田凹应弃之,
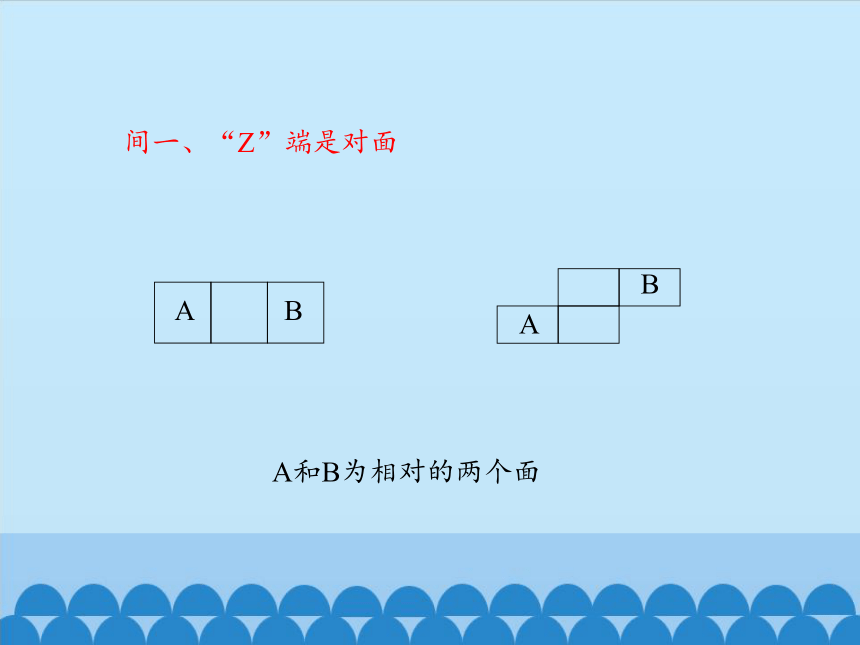
间一、“Z”端是对面,
间二、拐角邻面知。
一线不过四
×
×
田凹应弃之
×
×
×
×
间一、“Z”端是对面
A
B
A
B
A和B为相对的两个面
间二、拐角邻面知
C
C
D
D
C和D为相邻的两个面
右图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )
A. B. C. D.
B
如图所示的纸板上有10个无阴影的正方形,从中选出一个,与图中5个有阴影的正方形一起折一个正方体的包装盒,有多少种不同的选法。
想一想:下面几个图形是一些常见几何体的展开图,你能正确说出这些几何体的名字吗?
知识讲授:
圆柱体侧面
圆锥体侧面
展开
长方形
展开
扇形
巩固练习:
1.下图中的哪些图形可以沿虚线折叠成长方体包装盒。
考考你
2.如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来。
3.以下哪些图形经过折叠可以围成一个棱柱
(1)
(2)
(3)
(4)
拓展1:你有办法将图形(1)(3)修改后使其能折叠成棱柱
拓展2:图形(2)(4)是不同的平面图形,折叠出同样的棱柱,从中你得到了什么启示?
4.把下面的正三角形沿虚线折叠后的几何体是什么?
小结谈收获:
今天我们主要学习了哪些知识点呢?请同学们先自己回顾,然后在小组内互相交流。
谢 谢
第二课时
展开与折叠
教学目标:
1.经历图形的展开与折叠的活动,发展空间观念,积累数学活动经验。
2.认识正方体、圆柱、圆锥、棱柱的侧面展开图,能根据展开图判断能否折成几何体。
正方体的平面展开图共有以下11种:
知识回顾:
正方体的表面展开图“口诀”:
一线不过四,
田凹应弃之,
间一、“Z”端是对面,
间二、拐角邻面知。
一线不过四
×
×
田凹应弃之
×
×
×
×
间一、“Z”端是对面
A
B
A
B
A和B为相对的两个面
间二、拐角邻面知
C
C
D
D
C和D为相邻的两个面
右图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是( )
A. B. C. D.
B
如图所示的纸板上有10个无阴影的正方形,从中选出一个,与图中5个有阴影的正方形一起折一个正方体的包装盒,有多少种不同的选法。
想一想:下面几个图形是一些常见几何体的展开图,你能正确说出这些几何体的名字吗?
知识讲授:
圆柱体侧面
圆锥体侧面
展开
长方形
展开
扇形
巩固练习:
1.下图中的哪些图形可以沿虚线折叠成长方体包装盒。
考考你
2.如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来。
3.以下哪些图形经过折叠可以围成一个棱柱
(1)
(2)
(3)
(4)
拓展1:你有办法将图形(1)(3)修改后使其能折叠成棱柱
拓展2:图形(2)(4)是不同的平面图形,折叠出同样的棱柱,从中你得到了什么启示?
4.把下面的正三角形沿虚线折叠后的几何体是什么?
小结谈收获:
今天我们主要学习了哪些知识点呢?请同学们先自己回顾,然后在小组内互相交流。
谢 谢
