陕西省咸阳市三原县城关北城高级中学2021-2022学年高一11月教学质量检测数学试卷(Word版含答案)
文档属性
| 名称 | 陕西省咸阳市三原县城关北城高级中学2021-2022学年高一11月教学质量检测数学试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 475.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览



文档简介
北城高级中学2021-2022学年高一11月教学质量检测
数学试卷
一、单选题
1.将标有数字3,4,5的三张扑克牌随机分给甲、乙、丙三人,每人一张,事件A:“甲得到的扑克牌数字小于乙得到的扑克牌数字”与事件B:“乙得到的扑克牌数字为3”是( )
A. 互斥但不对立事件 B. 对立事件 C. 既不互斥又不对立事件 D. 以上都不对
2.圆 的圆心坐标和半径分别为( )
A. ,2 B. ,2
C. ,4 D. ,4
3.已知 外接圆的圆心为O,半径为1.设点O到边 BC ,CA,AB的距离分别为 , , .若 ,则 ( )
A. B.1 C. D.3
4.角 , , 是 三内角,且满足 ,则 的最大值是( )
A. B. C. D.
5.下列函数中,其图像既是中心对称图形又在区间 上单调递增的是( )
A. B. C. D.
6.在 中,D是 边上一点, , , , ,则 的值为( )
A. B.
C. D.
7.设函数 若 有两个零点,则实数a的取值范围是( )
A. B. C. D.
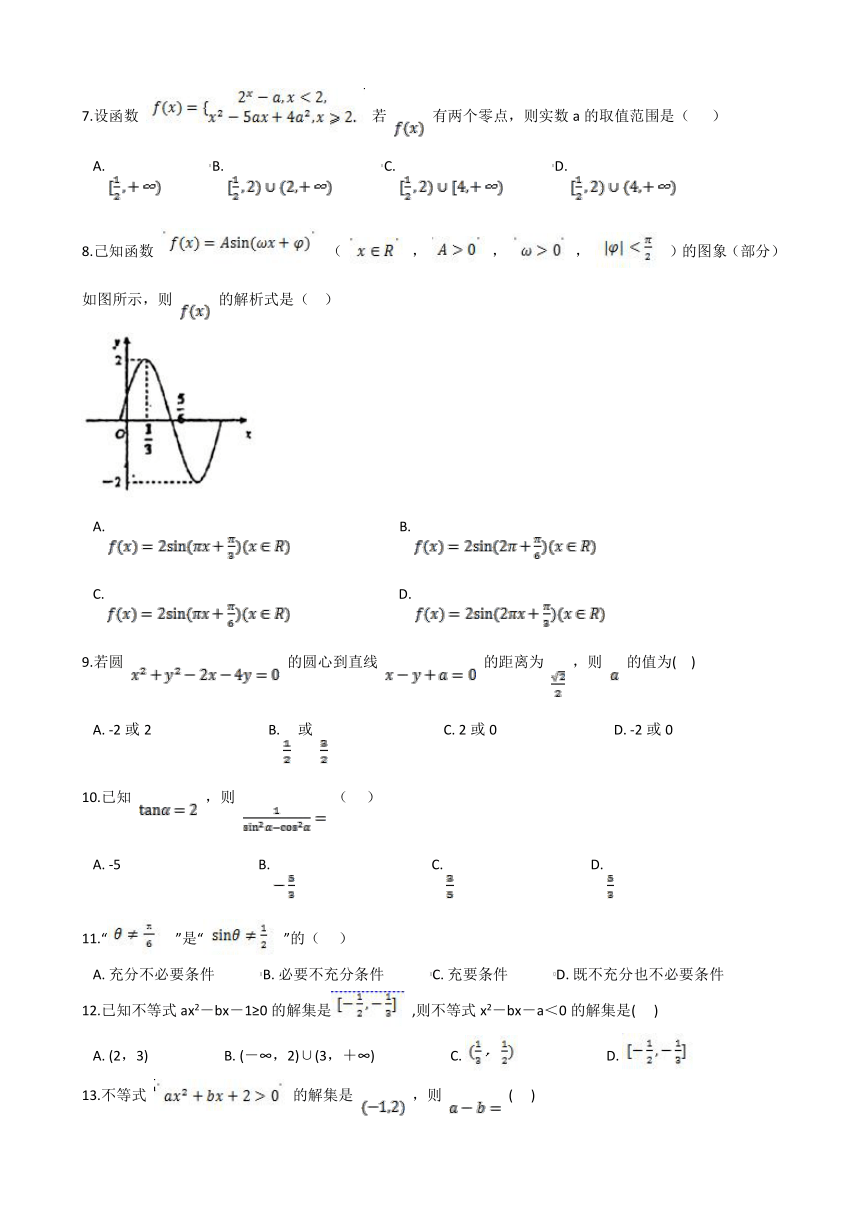
8.己知函数 ( , , , )的图象(部分)如图所示,则 的解析式是( )
A. B.
C. D.
9.若圆 的圆心到直线 的距离为 ,则 的值为( )
A. -2或2 B. 或 C. 2或0 D. -2或0
10.已知 ,则 ( )
A. -5 B. C. D.
11.“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
12.已知不等式ax2-bx-1≥0的解集是 ,则不等式x2-bx-a<0的解集是( )
A. (2,3) B. (-∞,2)∪(3,+∞) C. D.
13.不等式 的解集是 ,则 ( )
A. -3 B. -2 C. 2 D. 3
14.若 , ,分别在同一坐标系内给出函数 和函数 的图象可能的是( )
A. ②④ B. ①③ C. ①④ D. ②③
15.奇函数 的局部图像如图所示,则( )
A. B. C. D.
二、多选题
16.已知函数 ,下列说法正确的是( )
A. 函数 是奇函数 B. 关于x的不等式 的解集为
C. 函数 在R上是增函数 D. 函数 的图象的对称中心是
17.已知 a , b , c , ,则下列命题正确的是( )
A. 若 , ,则 B. 若 , ,则
C. 若 ,则 D. 若 ,则
18.设函数 与 的定义域分别为 , : , 唯一的 ,使得 .下列选项中的函数满足题设的是( )
A. , B. ,
C. , D. ,
19.下列函数中存在零点的函数有( )
A. B. C. D.
20.设函数 ,则下列选项正确的有( )
A. 的最小正周期是
B. 满足
C. 在 上单调递减,那么 的最大值是
D. 的图象可以由 的图象向右平移 个单位得到
三、填空题
21.设i是虚数单位,则复数(1﹣i)2﹣ 等于 .
22.已知A={x|0≤x≤4},B={y|0≤y≤2},从A到B的对应法则分别是:① ② ③ ④ 其中能构成一一映射的是________
23.已知平面区域D由以A(2,4)、B(5,2)、C(3,1)为顶点的三角形内部和边界组成,若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,则m= .
24.已知函数f(x)= (x∈(-1,1)),有下列结论:
⑴ x∈(-1,1),等式f(-x)+f(x)=0恒成立;
⑵ m∈[0,+∞),方程|f(x)|=m有两个不等实数根;
⑶ x1 , x2∈(-1,1),若x1≠x2 , 则一定有f(x1)≠f(x2);
⑷存在无数多个实数k,使得函数g(x)=f(x)-kx在(-1,1)上有三个零点
则其中正确结论的序号为________.
25.已知A(2,5),B(4,﹣1)若在y轴上存在一点P,使|PA|+|PB|最小,则P点的坐标为 .
四、解答题
26.已知函数 .
(1)判断 的奇偶性.
(2)用定义法证明 是定义域内的减函数.
27.经市场调查,某超市的一种商品在过去的一个月内(以30天计算),销售价格 与时间(天)的函数关系近似满足 ,销售量 与时间(天)的函数关系近似满足 .
(1)试写出该商品日销售金额 关于时间 的函数表达式;
(2)求该商品的日销售金额 的最大值与最小值.
28.已知函数f(x)=x3﹣3x及y=f(x)上一点P(1,﹣2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于P的直线方程.
29.已知函数 ,(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是 ,最小值是 .
(1)求ω,a,b的值;
(2)求出f(x)的单调递增区间.
答案解析部分
一、单选题
1.【答案】 A 2.【答案】 B 3.【答案】 B 4.【答案】 B 5.【答案】 C
6.【答案】 C 7.【答案】 C 8.【答案】 C 9.【答案】 C 10.【答案】 D
11.【答案】 B 12.【答案】 A 13.【答案】 B 14.【答案】 B 15.【答案】 A
二、多选题
16.【答案】 B,C,D 17.【答案】 B,C 18.【答案】 A,C 19.【答案】 B,C 20.【答案】 A,C
三、填空题
21.【答案】 ﹣4i
22.【答案】①②
23.【答案】
24.【答案】 (1)(3)(4)
25.【答案】 (0,3)
四、解答题
26.【答案】 (1)解:由题可知, 的定义域为R,关于原点对称.
,
所以 ,即 ,
故 是奇函数.
(2)解:任取 ,令 ,
则 .
因为 ,所以 ,所以 ,
故 是定义域内的减函数.
27.【答案】 (1)解:当 时, ;
当 时,
∴ .
(2)解:①当 时,由双勾函数的性质知 在 上单减,
在区间 上单增, .
∴当 时, 最小值为 ,当 时, 最大值为 ;
②当 时, , 在 单减,则 在区间 单减,
∴ ;
综上,当 时, 最大值为 ;当 时, 最小值为
28.【答案】 解:(1)由f(x)=x3﹣3x得,f′(x)=3x2﹣3,
过点P且以P(1,﹣2)为切点的直线的斜率f′(1)=0,
∴所求直线方程为y=﹣2.
(2)设过P(1,﹣2)的直线l与y=f(x)切于另一点(x0 , y0),
则f′(x0)=3x02﹣3.
又直线过(x0 , y0),P(1,﹣2),
故其斜率可表示为= ,
又=3x02﹣3,
即x03﹣3x0+2=3(x02﹣1) (x0﹣1),
解得x0=1(舍)或x0=﹣ ,
故所求直线的斜率为k=3×(﹣1)=﹣ ,
∴y﹣(﹣2)=﹣(x﹣1),
即9x+4y﹣1=0.
29.【答案】 (1)解:由函数最小正周期为π,
得 =π,∴ω=1
又f(x)的最大值是 ,最小值是 ,
则 ,解得:a= ,b=1
(2)解:由(1)知:f(x)= sin(2x+ )+ ,
当2kπ﹣ ≤2x+ ≤2kπ+ (k∈Z),
即kπ﹣ ≤x≤kπ+ (k∈Z)时,f(x)单调递增,
∴f(x)的单调递增区间为[kπ﹣ ,kπ+ ](k∈Z)
数学试卷
一、单选题
1.将标有数字3,4,5的三张扑克牌随机分给甲、乙、丙三人,每人一张,事件A:“甲得到的扑克牌数字小于乙得到的扑克牌数字”与事件B:“乙得到的扑克牌数字为3”是( )
A. 互斥但不对立事件 B. 对立事件 C. 既不互斥又不对立事件 D. 以上都不对
2.圆 的圆心坐标和半径分别为( )
A. ,2 B. ,2
C. ,4 D. ,4
3.已知 外接圆的圆心为O,半径为1.设点O到边 BC ,CA,AB的距离分别为 , , .若 ,则 ( )
A. B.1 C. D.3
4.角 , , 是 三内角,且满足 ,则 的最大值是( )
A. B. C. D.
5.下列函数中,其图像既是中心对称图形又在区间 上单调递增的是( )
A. B. C. D.
6.在 中,D是 边上一点, , , , ,则 的值为( )
A. B.
C. D.
7.设函数 若 有两个零点,则实数a的取值范围是( )
A. B. C. D.
8.己知函数 ( , , , )的图象(部分)如图所示,则 的解析式是( )
A. B.
C. D.
9.若圆 的圆心到直线 的距离为 ,则 的值为( )
A. -2或2 B. 或 C. 2或0 D. -2或0
10.已知 ,则 ( )
A. -5 B. C. D.
11.“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
12.已知不等式ax2-bx-1≥0的解集是 ,则不等式x2-bx-a<0的解集是( )
A. (2,3) B. (-∞,2)∪(3,+∞) C. D.
13.不等式 的解集是 ,则 ( )
A. -3 B. -2 C. 2 D. 3
14.若 , ,分别在同一坐标系内给出函数 和函数 的图象可能的是( )
A. ②④ B. ①③ C. ①④ D. ②③
15.奇函数 的局部图像如图所示,则( )
A. B. C. D.
二、多选题
16.已知函数 ,下列说法正确的是( )
A. 函数 是奇函数 B. 关于x的不等式 的解集为
C. 函数 在R上是增函数 D. 函数 的图象的对称中心是
17.已知 a , b , c , ,则下列命题正确的是( )
A. 若 , ,则 B. 若 , ,则
C. 若 ,则 D. 若 ,则
18.设函数 与 的定义域分别为 , : , 唯一的 ,使得 .下列选项中的函数满足题设的是( )
A. , B. ,
C. , D. ,
19.下列函数中存在零点的函数有( )
A. B. C. D.
20.设函数 ,则下列选项正确的有( )
A. 的最小正周期是
B. 满足
C. 在 上单调递减,那么 的最大值是
D. 的图象可以由 的图象向右平移 个单位得到
三、填空题
21.设i是虚数单位,则复数(1﹣i)2﹣ 等于 .
22.已知A={x|0≤x≤4},B={y|0≤y≤2},从A到B的对应法则分别是:① ② ③ ④ 其中能构成一一映射的是________
23.已知平面区域D由以A(2,4)、B(5,2)、C(3,1)为顶点的三角形内部和边界组成,若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,则m= .
24.已知函数f(x)= (x∈(-1,1)),有下列结论:
⑴ x∈(-1,1),等式f(-x)+f(x)=0恒成立;
⑵ m∈[0,+∞),方程|f(x)|=m有两个不等实数根;
⑶ x1 , x2∈(-1,1),若x1≠x2 , 则一定有f(x1)≠f(x2);
⑷存在无数多个实数k,使得函数g(x)=f(x)-kx在(-1,1)上有三个零点
则其中正确结论的序号为________.
25.已知A(2,5),B(4,﹣1)若在y轴上存在一点P,使|PA|+|PB|最小,则P点的坐标为 .
四、解答题
26.已知函数 .
(1)判断 的奇偶性.
(2)用定义法证明 是定义域内的减函数.
27.经市场调查,某超市的一种商品在过去的一个月内(以30天计算),销售价格 与时间(天)的函数关系近似满足 ,销售量 与时间(天)的函数关系近似满足 .
(1)试写出该商品日销售金额 关于时间 的函数表达式;
(2)求该商品的日销售金额 的最大值与最小值.
28.已知函数f(x)=x3﹣3x及y=f(x)上一点P(1,﹣2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于P的直线方程.
29.已知函数 ,(x∈R,a>0,ω>0)的最小正周期为π,函数f(x)的最大值是 ,最小值是 .
(1)求ω,a,b的值;
(2)求出f(x)的单调递增区间.
答案解析部分
一、单选题
1.【答案】 A 2.【答案】 B 3.【答案】 B 4.【答案】 B 5.【答案】 C
6.【答案】 C 7.【答案】 C 8.【答案】 C 9.【答案】 C 10.【答案】 D
11.【答案】 B 12.【答案】 A 13.【答案】 B 14.【答案】 B 15.【答案】 A
二、多选题
16.【答案】 B,C,D 17.【答案】 B,C 18.【答案】 A,C 19.【答案】 B,C 20.【答案】 A,C
三、填空题
21.【答案】 ﹣4i
22.【答案】①②
23.【答案】
24.【答案】 (1)(3)(4)
25.【答案】 (0,3)
四、解答题
26.【答案】 (1)解:由题可知, 的定义域为R,关于原点对称.
,
所以 ,即 ,
故 是奇函数.
(2)解:任取 ,令 ,
则 .
因为 ,所以 ,所以 ,
故 是定义域内的减函数.
27.【答案】 (1)解:当 时, ;
当 时,
∴ .
(2)解:①当 时,由双勾函数的性质知 在 上单减,
在区间 上单增, .
∴当 时, 最小值为 ,当 时, 最大值为 ;
②当 时, , 在 单减,则 在区间 单减,
∴ ;
综上,当 时, 最大值为 ;当 时, 最小值为
28.【答案】 解:(1)由f(x)=x3﹣3x得,f′(x)=3x2﹣3,
过点P且以P(1,﹣2)为切点的直线的斜率f′(1)=0,
∴所求直线方程为y=﹣2.
(2)设过P(1,﹣2)的直线l与y=f(x)切于另一点(x0 , y0),
则f′(x0)=3x02﹣3.
又直线过(x0 , y0),P(1,﹣2),
故其斜率可表示为= ,
又=3x02﹣3,
即x03﹣3x0+2=3(x02﹣1) (x0﹣1),
解得x0=1(舍)或x0=﹣ ,
故所求直线的斜率为k=3×(﹣1)=﹣ ,
∴y﹣(﹣2)=﹣(x﹣1),
即9x+4y﹣1=0.
29.【答案】 (1)解:由函数最小正周期为π,
得 =π,∴ω=1
又f(x)的最大值是 ,最小值是 ,
则 ,解得:a= ,b=1
(2)解:由(1)知:f(x)= sin(2x+ )+ ,
当2kπ﹣ ≤2x+ ≤2kπ+ (k∈Z),
即kπ﹣ ≤x≤kπ+ (k∈Z)时,f(x)单调递增,
∴f(x)的单调递增区间为[kπ﹣ ,kπ+ ](k∈Z)
同课章节目录
