华师大版八年级上册14.2.2勾股定理的应用课件(18张PPT)
文档属性
| 名称 | 华师大版八年级上册14.2.2勾股定理的应用课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 691.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:24:39 | ||
图片预览





文档简介
(共18张PPT)
华东师大版·八年级上册
14.2勾股定理的应用(2)
复习回顾
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.
a
b
c
A
B
C
如果在Rt△ABC中,∠C=90°,
字母表示:
那么a2+b2=c2.
勾股定理逆定理 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
a
b
c
A
B
C
字母表示:
如果△ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
那么△ABC是直角三角形.
探究新知
例1
如图所示,在3×3的方格图中,每个小方格的边长都为1,请在给定网格中按下列要求画出图形:
(1)画出所有从点A出发,另一个端点在格点(即小正方形的顶点)上,且长度为 的线段;
(2)画出所有以题(1)中所画线段为腰的等腰三角形.
A
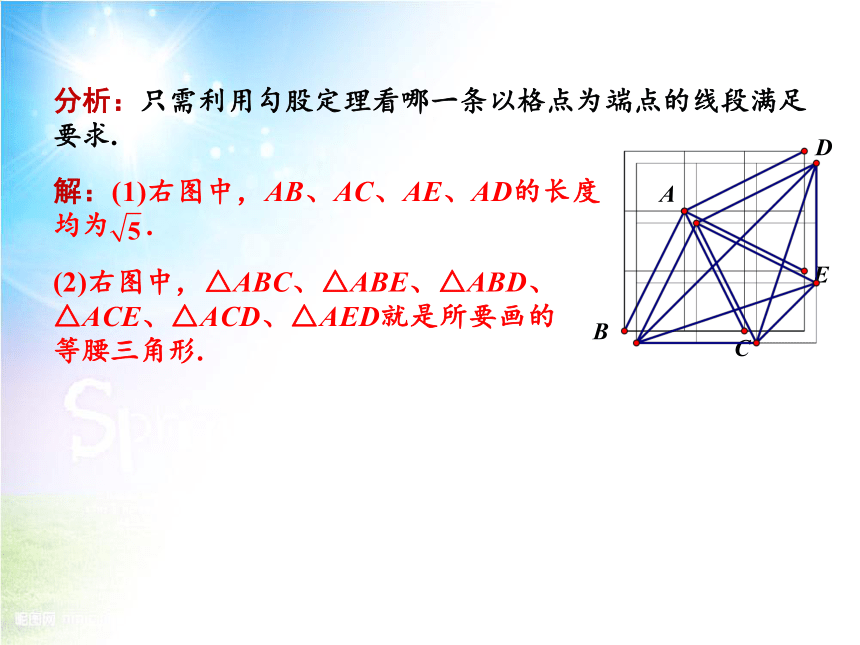
分析:只需利用勾股定理看哪一条以格点为端点的线段满足要求.
解:(1)右图中,AB、AC、AE、AD的长度均为 .
A
C
B
E
D
(2)右图中,△ABC、△ABE、△ABD、△ACE、△ACD、△AED就是所要画的等腰三角形.
试
一
试
如图,正方形网格中每一个小正方形的边长都是1,每个小格的顶点叫做格点.请以图中的格点为顶点画一个三角形,使三角形的三边长分别为 .
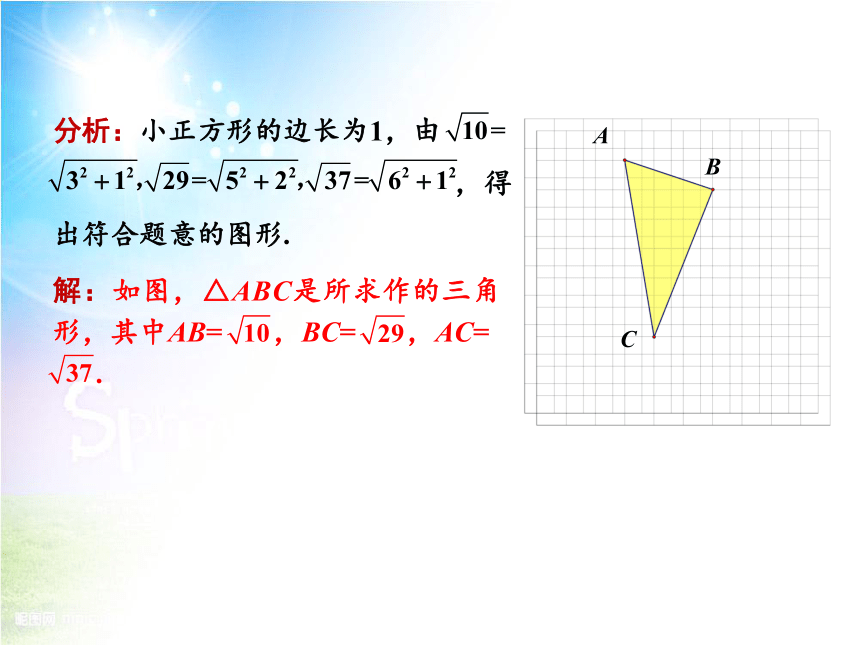
分析:小正方形的边长为1,由
,得出符合题意的图形.
解:如图,△ABC是所求作的三角形,其中AB= ,BC= ,AC=
.
A
B
C
例2
如图所示,已知CD=6m,AD=8m,∠ADC= 90°,BC=24m,AB=26m.求图中着色部分的面积.
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262=AB2,
∴△ABC为直角三角形(勾股定理的逆定理),
∴S阴影部分=S△ACB-S△ACD
试
一
试
如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向东南方向航行,乙轮船向西南方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
根据方向角可知两船所走的方向正好
构成了直角,根据勾股定理求出乙轮船航行的路程,进而求出速度.
解:由题意可知,AO⊥BO,OB=20×2=40海里,AB=50海里,
在Rt△AOB中, 海里,
∴乙轮船平均每小时航行30÷2=15海里.
随堂练习
1.形状为直角三角形的一块铁板的三边长分别为2米、4米、x米,试求出x的所有可能值.(精确到0.01米)
解:有两种情况,当斜边长为x米时,x= ≈
4.47;当斜边长为4米时,x= ≈3.46. 所以x约为4.47或3.46.
2.利用勾股定理,分别画出长度为 厘米和 厘米的线段.
解:如图所示,BD= 厘米,如图所示AB= 厘米.
1
1
1
1
2
3.在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a∶b=3∶4,c=15.求a、b.
解:设a=3x,b=4x,在Rt△ABC中,∠C=90°,
由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.
4.已知有一块四边形的空地ABCD,如图所示,经测量∠A =90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积.
解:如图,连接BD.
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在Rt△CBD中,CD2=132, BC2=122,
而122+52=132,即BC2+BD2=CD2,
∴∠DBC=90°.
∴S四边形ABCD=S△ABD+S△DBC
课堂小结
会用勾股定理解决简单应用题,学会构造直角三角形.
A
C
B
E
D
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华东师大版·八年级上册
14.2勾股定理的应用(2)
复习回顾
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.
a
b
c
A
B
C
如果在Rt△ABC中,∠C=90°,
字母表示:
那么a2+b2=c2.
勾股定理逆定理 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
a
b
c
A
B
C
字母表示:
如果△ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
那么△ABC是直角三角形.
探究新知
例1
如图所示,在3×3的方格图中,每个小方格的边长都为1,请在给定网格中按下列要求画出图形:
(1)画出所有从点A出发,另一个端点在格点(即小正方形的顶点)上,且长度为 的线段;
(2)画出所有以题(1)中所画线段为腰的等腰三角形.
A
分析:只需利用勾股定理看哪一条以格点为端点的线段满足要求.
解:(1)右图中,AB、AC、AE、AD的长度均为 .
A
C
B
E
D
(2)右图中,△ABC、△ABE、△ABD、△ACE、△ACD、△AED就是所要画的等腰三角形.
试
一
试
如图,正方形网格中每一个小正方形的边长都是1,每个小格的顶点叫做格点.请以图中的格点为顶点画一个三角形,使三角形的三边长分别为 .
分析:小正方形的边长为1,由
,得出符合题意的图形.
解:如图,△ABC是所求作的三角形,其中AB= ,BC= ,AC=
.
A
B
C
例2
如图所示,已知CD=6m,AD=8m,∠ADC= 90°,BC=24m,AB=26m.求图中着色部分的面积.
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262=AB2,
∴△ABC为直角三角形(勾股定理的逆定理),
∴S阴影部分=S△ACB-S△ACD
试
一
试
如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向东南方向航行,乙轮船向西南方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
根据方向角可知两船所走的方向正好
构成了直角,根据勾股定理求出乙轮船航行的路程,进而求出速度.
解:由题意可知,AO⊥BO,OB=20×2=40海里,AB=50海里,
在Rt△AOB中, 海里,
∴乙轮船平均每小时航行30÷2=15海里.
随堂练习
1.形状为直角三角形的一块铁板的三边长分别为2米、4米、x米,试求出x的所有可能值.(精确到0.01米)
解:有两种情况,当斜边长为x米时,x= ≈
4.47;当斜边长为4米时,x= ≈3.46. 所以x约为4.47或3.46.
2.利用勾股定理,分别画出长度为 厘米和 厘米的线段.
解:如图所示,BD= 厘米,如图所示AB= 厘米.
1
1
1
1
2
3.在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a∶b=3∶4,c=15.求a、b.
解:设a=3x,b=4x,在Rt△ABC中,∠C=90°,
由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.
4.已知有一块四边形的空地ABCD,如图所示,经测量∠A =90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积.
解:如图,连接BD.
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在Rt△CBD中,CD2=132, BC2=122,
而122+52=132,即BC2+BD2=CD2,
∴∠DBC=90°.
∴S四边形ABCD=S△ABD+S△DBC
课堂小结
会用勾股定理解决简单应用题,学会构造直角三角形.
A
C
B
E
D
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
