人教版八年级数学下册 18.1.1平行四边形及其性质 学案
文档属性
| 名称 | 人教版八年级数学下册 18.1.1平行四边形及其性质 学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:29:03 | ||
图片预览

文档简介
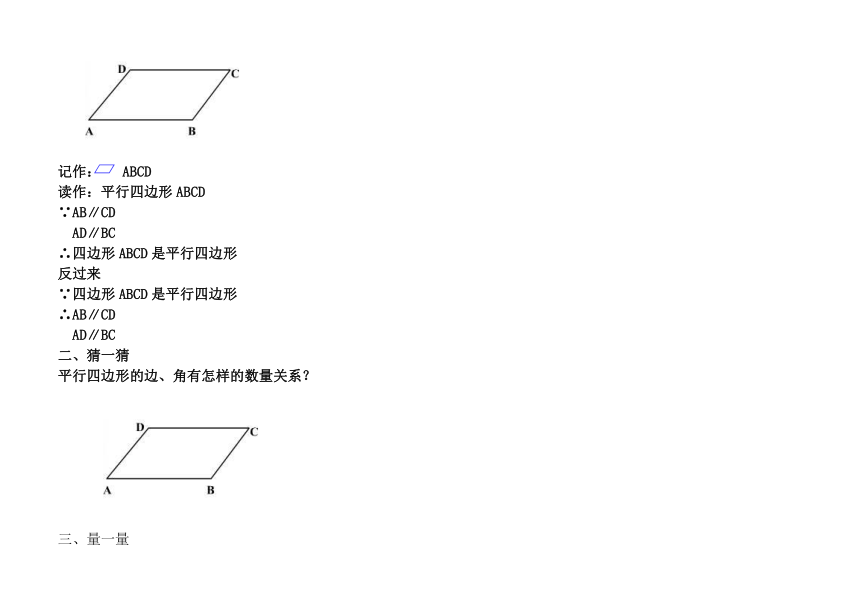
18.1.1平行四边形及其性质1(学案)
学习目标:
1、理解并掌握平行四边形的相关概念和性质,培养学生初步应用这些知识解决问题的能力。
2、学生亲自经历探索平行四边形有关概念和性质的过程,体会解决问题策略的多样性。
学习重难点:
1.重点:理解并掌握平行四边形的概念及其性质
2.难点:学生亲自经历探索平行四边形有关概念和性质的过程,体会解决问题策略的多样性。
学习过程:
1、 观察抽象 形成概念
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
记作: ABCD
读作:平行四边形ABCD
∵AB∥CD
AD∥BC
∴四边形ABCD是平行四边形
反过来
∵四边形ABCD是平行四边形
∴AB∥CD
AD∥BC
二、猜一猜
平行四边形的边、角有怎样的数量关系?
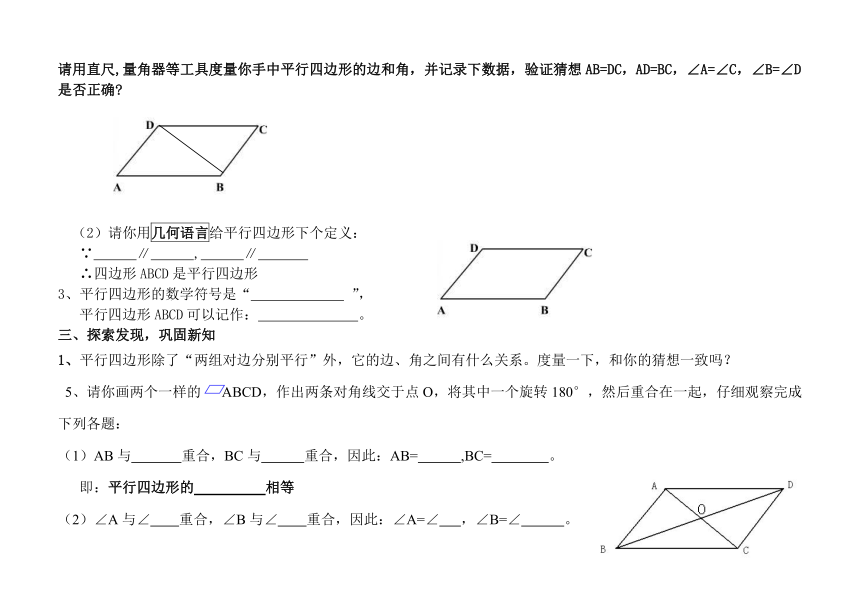
三、量一量
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
(2)请你用几何语言给平行四边形下个定义:
∵ ∥ , ∥
∴四边形ABCD是平行四边形
3、平行四边形的数学符号是“ ”,
平行四边形ABCD可以记作: 。
三、探索发现,巩固新知
1、平行四边形除了“两组对边分别平行”外,它的边、角之间有什么关系。度量一下,和你的猜想一致吗?
5、请你画两个一样的 ABCD,作出两条对角线交于点O,将其中一个旋转180°,然后重合在一起,仔细观察完成下列各题:
(1)AB与 重合,BC与 重合,因此:AB= ,BC= 。
即:平行四边形的 相等
(2)∠A与∠ 重合,∠B与∠ 重合,因此:∠A=∠ ,∠B=∠ 。
即:平行四边形的 相等
(3)AO与 重合,BO与 重合,因此:AO= ,BO= 。
即:平行四边形的 互相平分
6、归纳出平行四边形的性质:
文字叙述 几何表示
边 两组对边平行 AB∥CD AD∥BC
角
对角线
思考:1、平行四边形的邻角是什么关系?
2、你能用逻辑推理的方式证明平行四边形的一些性质吗?如果能,那就把你的想法与其他同学分享一下吧!
四、例题解析,提升认知
例题1:如图,在平行四边形ABCD中,已知∠A=50°,你还能知道哪些角的度数?
归纳:平行四边形的邻角 。
例题2:如图,在平行四边形ABCD中,已知AB=8,你还能知道哪些边的长?
五、巩固达标。
(一)基础巩固
1、已知平行四边形ABCD中,∠A=60°,∠B= ,∠C= ,∠D= 。
2、如图2,四边形ABCD是平行四边形,则∠ADC= ,
∠BCD= ,AB= ,BC= 。
3、已知平行四边形ABCD中,AB=5,AD=11,则它的周长是 。
4、在平行四边形ABCD中,已知∠A=40°,那么∠B=__________,
∠C=_________,∠D=_________。
1.已知□ABCD的两条对角线相交于点O,OA=5,OB=6,则AC= ,BD=
莲山课件 原文地址:http://www.5ykj.com/Health/ba/103555.htm
5、在平行四边形ABCD中,AB=8,周长等于24,求其余三条边的长。
画图:
(二)提高巩固
1、在 ABCD中,若AB= a,BC= b,则 ABCD的周长为_______
2、 ABCD中,已知∠A+∠C=260°,则∠A=____,∠B=___,∠C=____,
∠D=____。
3、在 ABCD中, ∠A:∠B= 4:5,那么∠B=__________,∠C=_________
4、如图, 平行四边形ABCD的周长为20cm,AE、AF是BC、CD边上的高,且cm,cm,试求平行四边形ABCD的面积。
学习目标:
1、理解并掌握平行四边形的相关概念和性质,培养学生初步应用这些知识解决问题的能力。
2、学生亲自经历探索平行四边形有关概念和性质的过程,体会解决问题策略的多样性。
学习重难点:
1.重点:理解并掌握平行四边形的概念及其性质
2.难点:学生亲自经历探索平行四边形有关概念和性质的过程,体会解决问题策略的多样性。
学习过程:
1、 观察抽象 形成概念
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
记作: ABCD
读作:平行四边形ABCD
∵AB∥CD
AD∥BC
∴四边形ABCD是平行四边形
反过来
∵四边形ABCD是平行四边形
∴AB∥CD
AD∥BC
二、猜一猜
平行四边形的边、角有怎样的数量关系?
三、量一量
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
(2)请你用几何语言给平行四边形下个定义:
∵ ∥ , ∥
∴四边形ABCD是平行四边形
3、平行四边形的数学符号是“ ”,
平行四边形ABCD可以记作: 。
三、探索发现,巩固新知
1、平行四边形除了“两组对边分别平行”外,它的边、角之间有什么关系。度量一下,和你的猜想一致吗?
5、请你画两个一样的 ABCD,作出两条对角线交于点O,将其中一个旋转180°,然后重合在一起,仔细观察完成下列各题:
(1)AB与 重合,BC与 重合,因此:AB= ,BC= 。
即:平行四边形的 相等
(2)∠A与∠ 重合,∠B与∠ 重合,因此:∠A=∠ ,∠B=∠ 。
即:平行四边形的 相等
(3)AO与 重合,BO与 重合,因此:AO= ,BO= 。
即:平行四边形的 互相平分
6、归纳出平行四边形的性质:
文字叙述 几何表示
边 两组对边平行 AB∥CD AD∥BC
角
对角线
思考:1、平行四边形的邻角是什么关系?
2、你能用逻辑推理的方式证明平行四边形的一些性质吗?如果能,那就把你的想法与其他同学分享一下吧!
四、例题解析,提升认知
例题1:如图,在平行四边形ABCD中,已知∠A=50°,你还能知道哪些角的度数?
归纳:平行四边形的邻角 。
例题2:如图,在平行四边形ABCD中,已知AB=8,你还能知道哪些边的长?
五、巩固达标。
(一)基础巩固
1、已知平行四边形ABCD中,∠A=60°,∠B= ,∠C= ,∠D= 。
2、如图2,四边形ABCD是平行四边形,则∠ADC= ,
∠BCD= ,AB= ,BC= 。
3、已知平行四边形ABCD中,AB=5,AD=11,则它的周长是 。
4、在平行四边形ABCD中,已知∠A=40°,那么∠B=__________,
∠C=_________,∠D=_________。
1.已知□ABCD的两条对角线相交于点O,OA=5,OB=6,则AC= ,BD=
莲山课件 原文地址:http://www.5ykj.com/Health/ba/103555.htm
5、在平行四边形ABCD中,AB=8,周长等于24,求其余三条边的长。
画图:
(二)提高巩固
1、在 ABCD中,若AB= a,BC= b,则 ABCD的周长为_______
2、 ABCD中,已知∠A+∠C=260°,则∠A=____,∠B=___,∠C=____,
∠D=____。
3、在 ABCD中, ∠A:∠B= 4:5,那么∠B=__________,∠C=_________
4、如图, 平行四边形ABCD的周长为20cm,AE、AF是BC、CD边上的高,且cm,cm,试求平行四边形ABCD的面积。
