鲁教版(五四制)数学七年级上册 2.3 简单的轴对称图形 第三课时 课件(共22张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 2.3 简单的轴对称图形 第三课时 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 432.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:34:20 | ||
图片预览







文档简介
(共22张PPT)
第三课时
简单的轴对称图形
Contents
目录
01
02
03
04
课堂小结
课前导入
随堂练习
05
新知探究
小组竞赛
课前导入
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
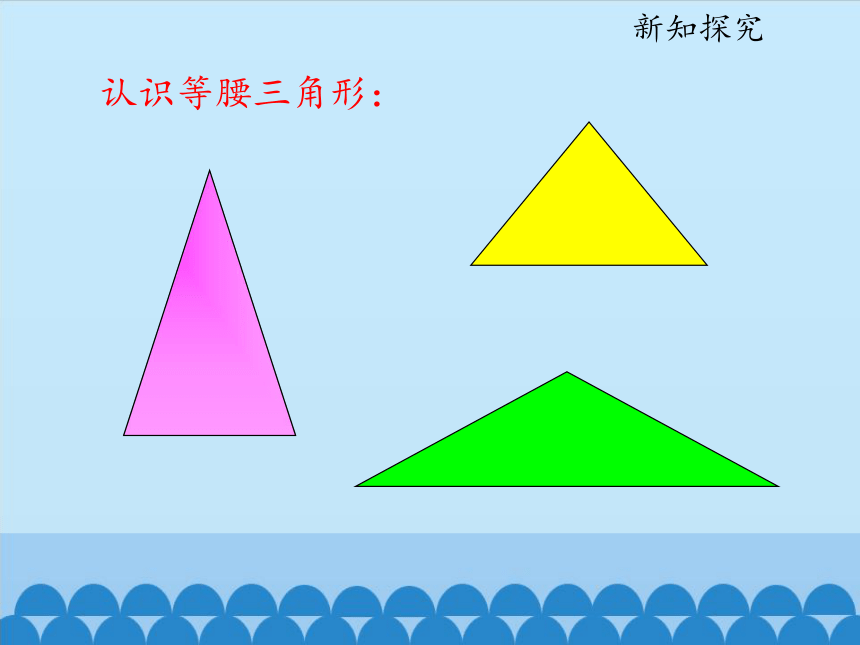
认识等腰三角形:
新知探究
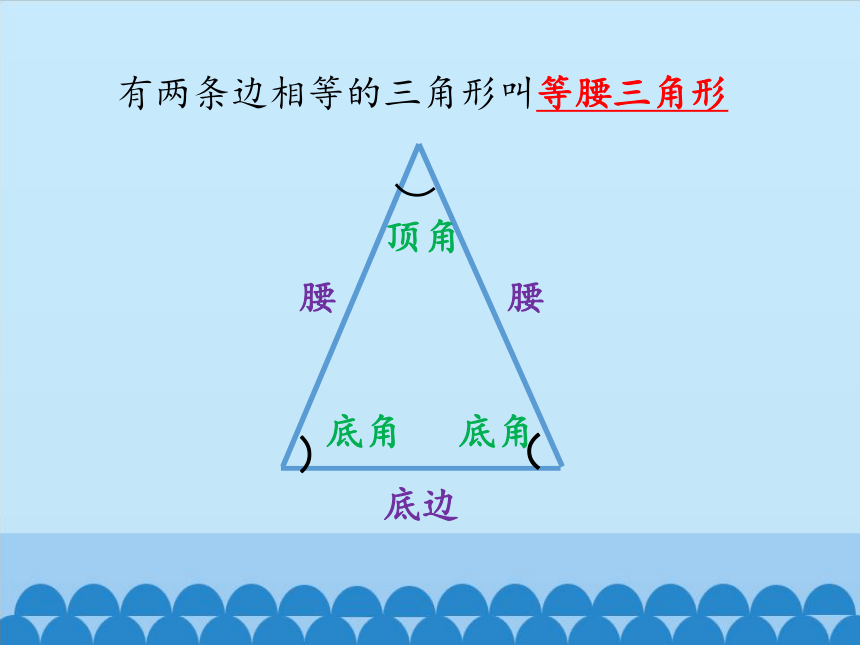
有两条边相等的三角形叫等腰三角形
(
(
顶角
底角
底角
腰
腰
底边
)
生活中的等腰三角形
1.等腰三角形是轴对称图形吗?如果是,请找出对称轴。
2.等腰三角形顶角平分线所在的直线是它的对称轴吗?
3.等腰三角形底边上的中线所在直线是它的对称轴吗?底边上的高所在直线呢?
4.沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由。
思考
拿出你的等腰三角形纸片,折折看,你能发现什么现象?
等腰三角形是一种特殊的三角形,它除具有一般三角形的性质外,还有一些特殊的性质吗?
看看你本组其他同学的情况,共同交流,能得出什么结论?
1.等腰三角形是轴对称图形。
2.等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
3.等腰三角形的两个底角相等。
等腰三角形的特征
三边都相等的三角形是等边三角形也叫正三角形
(1)等边三角形有几条对称轴?
(2)你能发现等边三角形的哪些特征?
折叠一下试试!
动手实践一
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
3.等边三角形的各角都相等,都等于60°。
你有哪些办法可以得到一个等腰三角形?与同伴交流。
动手实践二
1.按下面的步骤做一做:
(1)将长方形纸片对折
(2)然后沿对角线折叠,再沿折痕剪开。
2.你能尝试用圆规吗?
你有哪些办法可以得到一个等腰三角形?与同伴交流。
1.如图,是由大小不等的等边三角形组成的图案,请找出它的对称轴。
2.如图,在等腰ΔABC 中,AB=AC 顶角
∠A =100°那么底角∠B =_______,
∠C =_______。
40°
40°
3.在△ABC 中,AB =AC,∠B =72°,那么
∠A =______。
4.在等腰三角形△ABC中,有一个角为50°,那么另外两个角分别是_________或_________。
B
C
A
36°
65°和65°
50°和80°
5.如图,在△ABC中,AB=AC时,
(1)因为AD⊥BC
所以∠____=∠_____;____=____。
(2)因为AD是中线
所以____⊥____;∠_____=∠_____。
(3)因为AD是角平分线
所以____⊥____;_____=____。
BAD
CAD
CD
BD
AD
BC
BAD
CAD
AD
BC
BD
CD
A
B
C
D
下面有几道练习题,请同学们以小组为单位进行讨论练习!
小组竞赛
1.如果ΔABC是轴对称图形,则它的对称轴一定是( )
A.某一条边上的高。
B.某一条边上的中线。
C.平分一角和这个角的对边的直线。
D.某一个角的平分线。
C
2.若等腰三角形的一个内角为40°,则它的另外两个内角为________________________。
3.若等腰三角形的一个内角为120°,则它的另外两个内角为____________。
70°,70°或40°,100°
30°,30°
4.一等腰三角形的两边长为2和4,则该等腰三角形的周长为________。
5.一等腰三角形的两边长为3和4,则该等腰三角形的周长为________。
10
10或11
6.已知等腰三角形的腰长比底边长多2cm,并且它的周长为16cm,求这个等腰三角形的各边长。
解:设三角形的底边长为xcm,则其腰长为(x+2)cm,根据题意得:
2(x+2)+x=16
解得x=4
∴等腰三角形三边长为4cm,6cm,6cm。
如图,P,Q 是△ABC 边上的两点,且BP=PQ=QC=AP=AQ,求∠BAC 的度数。
A
P
B
C
Q
开动脑筋
你学到了哪些知识?
1.等腰三角形的性质。
2.等边三角形的性质。
3.相关计算。
课堂小结
谢 谢
第三课时
简单的轴对称图形
Contents
目录
01
02
03
04
课堂小结
课前导入
随堂练习
05
新知探究
小组竞赛
课前导入
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
认识等腰三角形:
新知探究
有两条边相等的三角形叫等腰三角形
(
(
顶角
底角
底角
腰
腰
底边
)
生活中的等腰三角形
1.等腰三角形是轴对称图形吗?如果是,请找出对称轴。
2.等腰三角形顶角平分线所在的直线是它的对称轴吗?
3.等腰三角形底边上的中线所在直线是它的对称轴吗?底边上的高所在直线呢?
4.沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由。
思考
拿出你的等腰三角形纸片,折折看,你能发现什么现象?
等腰三角形是一种特殊的三角形,它除具有一般三角形的性质外,还有一些特殊的性质吗?
看看你本组其他同学的情况,共同交流,能得出什么结论?
1.等腰三角形是轴对称图形。
2.等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
3.等腰三角形的两个底角相等。
等腰三角形的特征
三边都相等的三角形是等边三角形也叫正三角形
(1)等边三角形有几条对称轴?
(2)你能发现等边三角形的哪些特征?
折叠一下试试!
动手实践一
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
3.等边三角形的各角都相等,都等于60°。
你有哪些办法可以得到一个等腰三角形?与同伴交流。
动手实践二
1.按下面的步骤做一做:
(1)将长方形纸片对折
(2)然后沿对角线折叠,再沿折痕剪开。
2.你能尝试用圆规吗?
你有哪些办法可以得到一个等腰三角形?与同伴交流。
1.如图,是由大小不等的等边三角形组成的图案,请找出它的对称轴。
2.如图,在等腰ΔABC 中,AB=AC 顶角
∠A =100°那么底角∠B =_______,
∠C =_______。
40°
40°
3.在△ABC 中,AB =AC,∠B =72°,那么
∠A =______。
4.在等腰三角形△ABC中,有一个角为50°,那么另外两个角分别是_________或_________。
B
C
A
36°
65°和65°
50°和80°
5.如图,在△ABC中,AB=AC时,
(1)因为AD⊥BC
所以∠____=∠_____;____=____。
(2)因为AD是中线
所以____⊥____;∠_____=∠_____。
(3)因为AD是角平分线
所以____⊥____;_____=____。
BAD
CAD
CD
BD
AD
BC
BAD
CAD
AD
BC
BD
CD
A
B
C
D
下面有几道练习题,请同学们以小组为单位进行讨论练习!
小组竞赛
1.如果ΔABC是轴对称图形,则它的对称轴一定是( )
A.某一条边上的高。
B.某一条边上的中线。
C.平分一角和这个角的对边的直线。
D.某一个角的平分线。
C
2.若等腰三角形的一个内角为40°,则它的另外两个内角为________________________。
3.若等腰三角形的一个内角为120°,则它的另外两个内角为____________。
70°,70°或40°,100°
30°,30°
4.一等腰三角形的两边长为2和4,则该等腰三角形的周长为________。
5.一等腰三角形的两边长为3和4,则该等腰三角形的周长为________。
10
10或11
6.已知等腰三角形的腰长比底边长多2cm,并且它的周长为16cm,求这个等腰三角形的各边长。
解:设三角形的底边长为xcm,则其腰长为(x+2)cm,根据题意得:
2(x+2)+x=16
解得x=4
∴等腰三角形三边长为4cm,6cm,6cm。
如图,P,Q 是△ABC 边上的两点,且BP=PQ=QC=AP=AQ,求∠BAC 的度数。
A
P
B
C
Q
开动脑筋
你学到了哪些知识?
1.等腰三角形的性质。
2.等边三角形的性质。
3.相关计算。
课堂小结
谢 谢
