2021-2022学年华东师大版八年级数学上册第14章勾股定理单元测试题(word解析版)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册第14章勾股定理单元测试题(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 151.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览


文档简介
2021-2022学年华东师大八年级上册数学
《第14章 勾股定理》单元测试卷
一.选择题
1.已知Rt△ABC的周长是4+4,斜边上的中线长是2,则S△ABC为( )
A.16 B.8 C.4 D.12
2.已知△ABC的三边分别是6,8,10,则△ABC的面积是( )
A.24 B.30 C.40 D.48
3.用反证法证明命题“如图,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一个步骤是( )
A.假设AB不平行于CD B.假设AB不平行于EF
C.假设CD∥EF D.假设CD不平行于EF
4.如图,数轴上A点表示的数为﹣2,B点表示的数是1.过点B作BC⊥AB,且BC=2,以点A为圆心,AC的长为半径作弧,弧与数轴的交点D表示的数为( )
A. B. +2 C.﹣2 D.﹣ +2
5.下列各组线段中,能组成直角三角形的一组是( )
A.1,2,3 B.2,3,4 C.3,5,6 D.
6.用反证法证明“直角三角形中至少有一个锐角不大于45°”,应先假设( )
A.直角三角形中两个锐角都大于45°
B.直角三角形中两个锐角都不大于45°
C.直角三角形中有一个锐角大于45°
D.直角三角形中有一个锐角不大于45°
7.若实数m、n满足|m﹣3|+=0,且m、n恰好是Rt△ABC的两条边长,则第三条边长为( )
A.5 B. C.5或 D.以上都不对
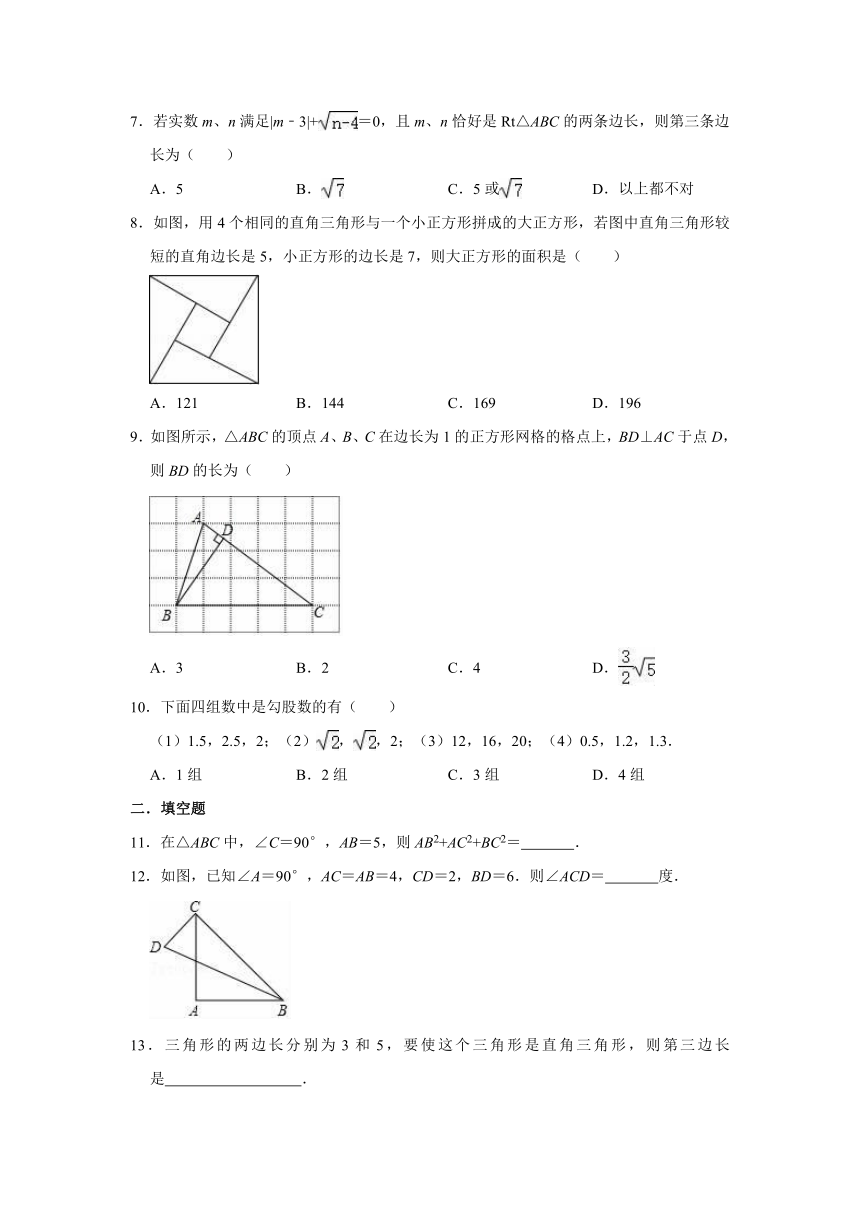
8.如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是( )
A.121 B.144 C.169 D.196
9.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A.3 B.2 C.4 D.
10.下面四组数中是勾股数的有( )
(1)1.5,2.5,2;(2),,2;(3)12,16,20;(4)0.5,1.2,1.3.
A.1组 B.2组 C.3组 D.4组
二.填空题
11.在△ABC中,∠C=90°,AB=5,则AB2+AC2+BC2= .
12.如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD= 度.
13.三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三边长是 .
14.用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步 .
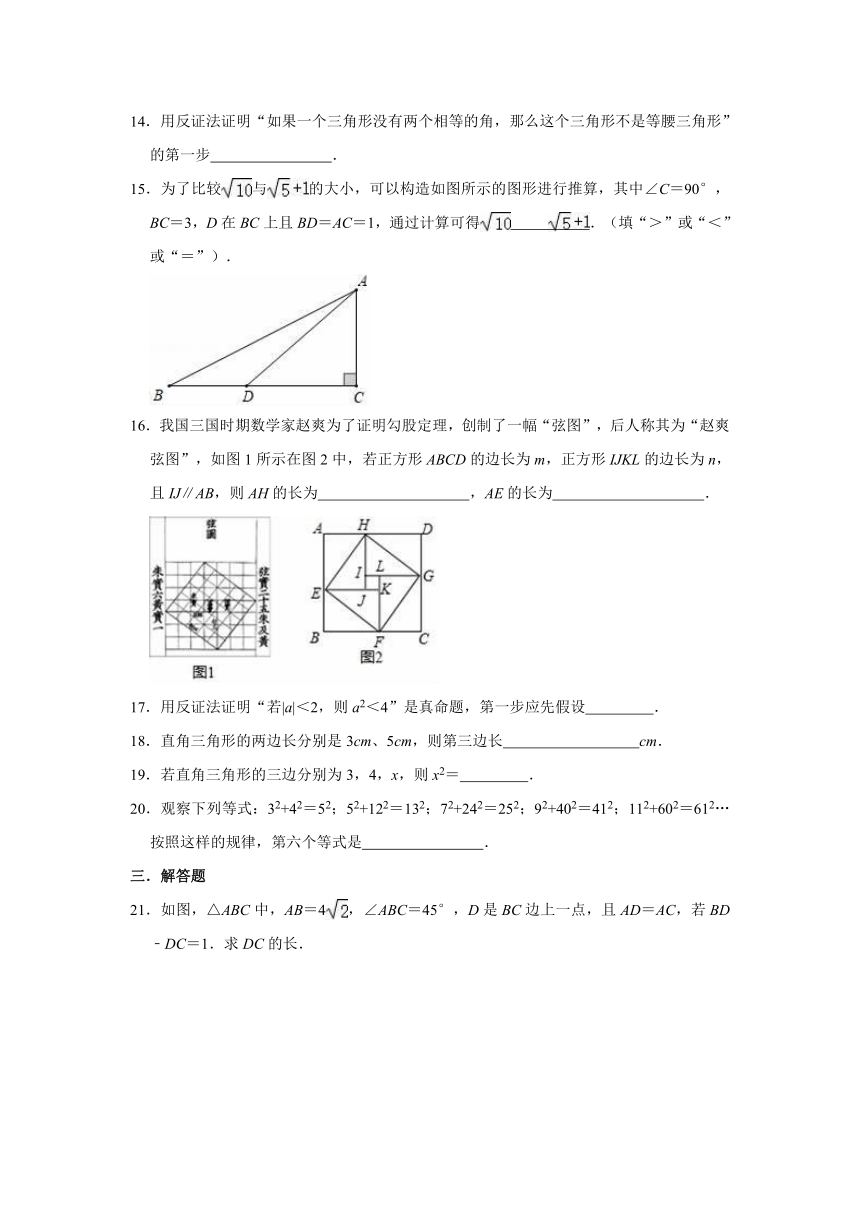
15.为了比较与的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,D在BC上且BD=AC=1,通过计算可得 .(填“>”或“<”或“=”).
16.我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示在图2中,若正方形ABCD的边长为m,正方形IJKL的边长为n,且IJ∥AB,则AH的长为 ,AE的长为 .
17.用反证法证明“若|a|<2,则a2<4”是真命题,第一步应先假设 .
18.直角三角形的两边长分别是3cm、5cm,则第三边长 cm.
19.若直角三角形的三边分别为3,4,x,则x2= .
20.观察下列等式:32+42=52;52+122=132;72+242=252;92+402=412;112+602=612…按照这样的规律,第六个等式是 .
三.解答题
21.如图,△ABC中,AB=4,∠ABC=45°,D是BC边上一点,且AD=AC,若BD﹣DC=1.求DC的长.
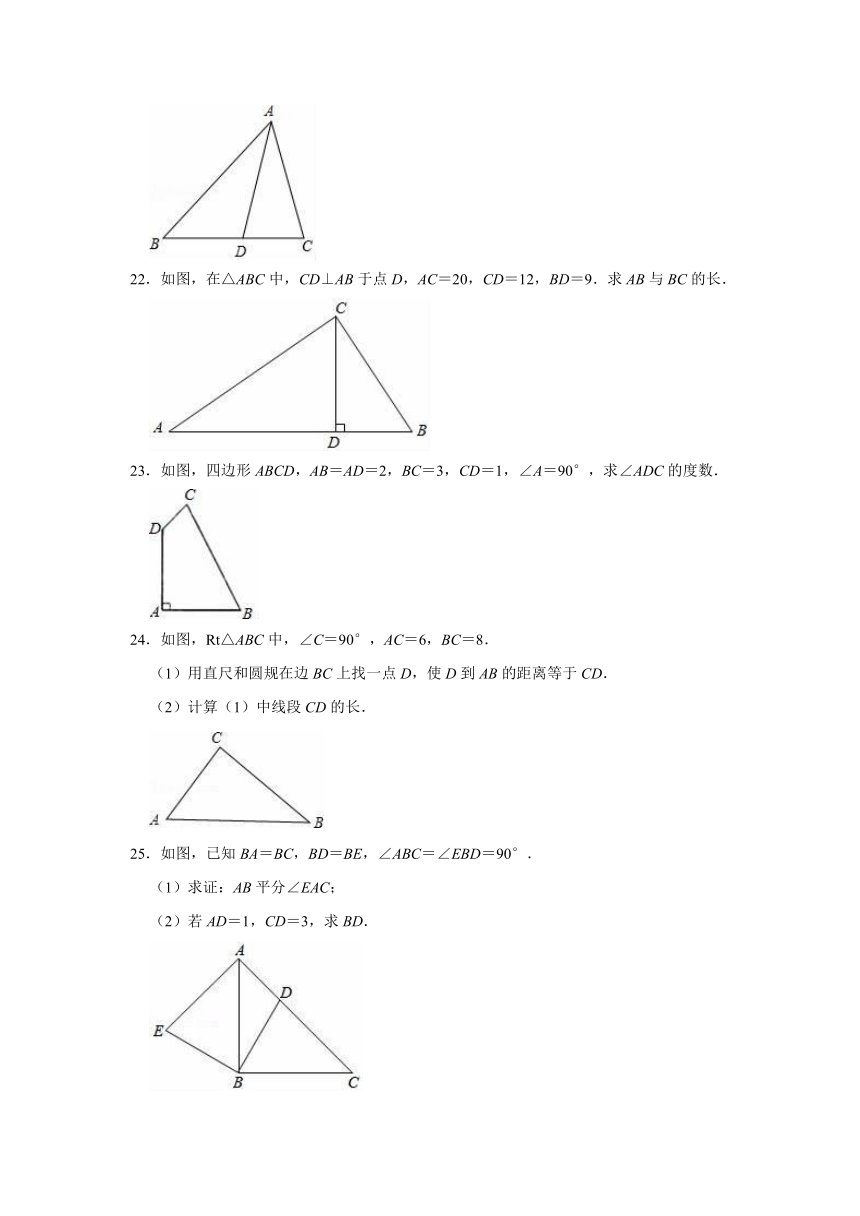
22.如图,在△ABC中,CD⊥AB于点D,AC=20,CD=12,BD=9.求AB与BC的长.
23.如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
24.如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.
(2)计算(1)中线段CD的长.
25.如图,已知BA=BC,BD=BE,∠ABC=∠EBD=90°.
(1)求证:AB平分∠EAC;
(2)若AD=1,CD=3,求BD.
26.用图1中四个完全一样的直角三角形可以拼成图2的大正方形
解答下列问题:
(1)请用含a、b、c的代数式表示大正方形的面积.
方法1 ;方法2 .
(2)根据图2,利用图形的面积关系,推导a、b、c之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且(a+b)2=49,求小正方形的面积.
参考答案与试题解析
一.选择题
1.解:∵Rt△ABC的周长是4+4,斜边上的中线长是2,
∴斜边长为4,
设两个直角边的长为x,y,则x+y=4,x2+y2=16,
解得:xy=8,
∴S△ABC=xy=4.
故选:C.
2.解:∵62+82=102,
∴△ABC是直角三角形,
∴△ABC的面积=×6×8=24.
故选:A.
3.解:∵用反证法证明命题:如果AB∥CD,AB∥EF,那么CD∥EF.
∴证明的第一步应是:从结论反面出发,假设CD不平行于EF.
故选:D.
4.解:∵CA==,
∴AC=AD=,
∴D到原点的距离是﹣2.
∴点D所表示的数是﹣2.
故选:C.
5.解:12+22≠32,故选项A中三条线段不能组成直角三角形;
22+32≠42,故选项B中三条线段不能组成直角三角形;
32+52≠62,故选项C中三条线段不能组成直角三角形;
12+()2=22,故选项D中三条线段能组成直角三角形;
故选:D.
6.解:用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,应先假设两个锐角都大于45°.
故选:A.
7.解:∵|m﹣3|+=0,
∴m﹣3=0且n﹣4=0,
则m=3,n=4,
当4是直角边时,斜边长==5,
当4是斜边时,另一条直角边==,
综上,第三条边长为5或,
故选:C.
8.解:∵直角三角形较短的直角边长是5,小正方形的边长是7,
∴直角三角形的较长直角边=5+7=12,
∴直角三角形斜边长=13,
∴大正方形的边长是13,
∴大正方形的面积是13×13=169.
故选:C.
9.解:∵BC=5,AC==5,
∴S△ABC=×5×3=×AC×BD,
∴BD=3,
解法二:过A点做AE⊥BC交于点E,则易证三角形AEC全等三角形BDC,所以BD等于AE=3.
故选:A.
10.解:(1)1.52+22=2.52,但不是正整数,故错误;
(2)()2+()2=22,能构成直角三角形,但不是整数,故错误;
(3)122+162=202,三边是整数,同时能构成直角三角形,故正确;
(4)0.52+1.22=1.32,但不是正整数,故错误.
故选:A.
二.填空题
11.解:∵∠C=90°,
∴AB2=AC2+BC2,
∴AB2+AC2+BC2=2AB2=2×52=2×25=50.
故答案为:50.
12.解:∵∠A=90°,AC=AB=4,
∴∠ACB=∠ABC=45°,
在Rt△ABC中,BC==4,
CD2+BC2=22+(4)2=36,BD2=62=36,
∴CD2+BC2=BD2,
∴∠BCD=90°,
∴∠ACD=45°,
故答案为:45.
13.解:当第三边是直角边时,根据勾股定理,第三边的长==4,三角形的边长分别为3,4,5能构成三角形;
当第三边是斜边时,根据勾股定理,第三边的长==,三角形的边长分别为3,5,亦能构成三角形;
综合以上两种情况,第三边的长应为4或.
14.解:用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步是假设这个三角形是等腰三角形.
故答案为这个三角形是等腰三角形.
15.解:∵∠C=90°,BC=3,BD=AC=1,
∴CD=2,AD==,AB==,
∴BD+AD=+1,
又∵△ABD中,AD+BD>AB,
∴+1>,
故答案为:<.
16.解:∵四边形ABCD和四边形IJKL是正方形,
∴∠A=∠LIJ=90°,
∵IJ∥AB,
∴∠AEJ=90°,
∴四边形AEJH是矩形,
∴AH=EJ,AE=HJ,
同理,DH=IG,
∵IG=HJ,
∴DH=AE,
∵正方形ABCD的边长为m,正方形IJKL的边长为n,
∴AH+AE=m,AE﹣AH=n,
∴AE=,AH=,
故答案为:,.
17.解:用反证法证明“若|a|<2,则a2<4.”是真命题时,第一步应先假设:a2≥4.
故答案为:a2≥4.
18.解:①当3cm和5cm都是直角边时,第三边为斜边,
由勾股定理得:第三边为=(cm);
②当3cm为直角边和5cm为斜边时,第三边为直角边,
由勾股定理得:第三边为=4(cm).
故答案为:4或.
19.解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理得:
32+42=x2,所以x2=25;
(2)若4是斜边,则第三边x为直角边,由勾股定理得:
32+x2=42,所以x2=7;
故答案为25或7;
20.解:∵第一个等式是:32+42=52;
第二个等式是52+122=132;
第三个等式是72+242=252;
第四个等式是92+402=412;
第五个等式是112+602=612…
按照这样的规律,第六个等式是:132+842=852,
故答案为:132+842=852.
三.解答题
21.解:过点A作AE⊥BC于点E,如图所示.
∵AD=AC,AE⊥BC,
∴∠AEB=90°,DE=CE.
∵∠ABC=45°,
∴∠BAE=45°,
∴AE=BE.
在Rt△ABE中,AB=4,
∴AE2+BE2=AB2,即BE2+BE2=(4)2,
∴BE=4,
∴BD+DC=4.
又∵BD﹣DC=1,
∴DC+1+DC=4,
∴DC=2.
22.解:∵CD⊥AB,AC=20,CD=12,BD=9,
∴∠ADC=∠BDC=90°,
在Rt△CDB中,
由勾股定理得:BC===15,
在Rt△ADC中,
由勾股定理得:AD===16,
∴AB=AD+DB=16+9=25.
答:AB的长为25,BC的长为15.
23.解:连接BD,
在Rt△BAD中,
∵AB=AD=2,
∴∠ADB=45°,BD==2,
在△BCD中,
DB2+CD2=(2)2+12=9=CB2,
∴△BCD是直角三角形,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=45°+90°=135°.
24.解:(1)画角平分线正确,保留画图痕迹
(2)设CD=x,作DE⊥AB于E,
则DE=CD=x,
∵∠C=90°,AC=6,BC=8.
∴AB=10,
∴EB=10﹣6=4.
∵DE2+BE2=DB2,
∴x2+42=(8﹣x)2,
x=3,
即CD长为3.
25.解:(1)证明:∵∠ABC=∠EBD=90°,
∴∠ABD+∠CBD=∠ABD+∠ABE,
∴∠CBD=∠ABE,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴∠EAB=∠BAC,
∴AB平分∠EAC;
(2)∵AD=1,CD=3,
∴AC=4.
∵BA=BC,∠ABC=90°,
∴AB=BC==2,∠C=45°,
过点B作BF⊥AC于点F,如图:
则△BCF为等腰直角三角形,
∴BF=CF=2,
∴DF=CD﹣CF=1,
在Rt△BFD中,由勾股定理得:
BD=
=
=.
∴BD的长等于.
26.解:(1)方法1:大正方形的面积=(a﹣b)2+4×ab=a2+b2,
方法2:大正方形的面积=c2;
故答案为:a2+b2,c2;
(2)因为大正方形的面积相等,
所以a2+b2=c2;
(3)由(2)知,a2+b2=c2.
又(a+b)2=49,
所以 2ab=49﹣(a2+b2)=49﹣c2=49﹣25=24.
所以 小正方形的面积=25﹣24=1.
《第14章 勾股定理》单元测试卷
一.选择题
1.已知Rt△ABC的周长是4+4,斜边上的中线长是2,则S△ABC为( )
A.16 B.8 C.4 D.12
2.已知△ABC的三边分别是6,8,10,则△ABC的面积是( )
A.24 B.30 C.40 D.48
3.用反证法证明命题“如图,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一个步骤是( )
A.假设AB不平行于CD B.假设AB不平行于EF
C.假设CD∥EF D.假设CD不平行于EF
4.如图,数轴上A点表示的数为﹣2,B点表示的数是1.过点B作BC⊥AB,且BC=2,以点A为圆心,AC的长为半径作弧,弧与数轴的交点D表示的数为( )
A. B. +2 C.﹣2 D.﹣ +2
5.下列各组线段中,能组成直角三角形的一组是( )
A.1,2,3 B.2,3,4 C.3,5,6 D.
6.用反证法证明“直角三角形中至少有一个锐角不大于45°”,应先假设( )
A.直角三角形中两个锐角都大于45°
B.直角三角形中两个锐角都不大于45°
C.直角三角形中有一个锐角大于45°
D.直角三角形中有一个锐角不大于45°
7.若实数m、n满足|m﹣3|+=0,且m、n恰好是Rt△ABC的两条边长,则第三条边长为( )
A.5 B. C.5或 D.以上都不对
8.如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是( )
A.121 B.144 C.169 D.196
9.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A.3 B.2 C.4 D.
10.下面四组数中是勾股数的有( )
(1)1.5,2.5,2;(2),,2;(3)12,16,20;(4)0.5,1.2,1.3.
A.1组 B.2组 C.3组 D.4组
二.填空题
11.在△ABC中,∠C=90°,AB=5,则AB2+AC2+BC2= .
12.如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD= 度.
13.三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三边长是 .
14.用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步 .
15.为了比较与的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,D在BC上且BD=AC=1,通过计算可得 .(填“>”或“<”或“=”).
16.我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示在图2中,若正方形ABCD的边长为m,正方形IJKL的边长为n,且IJ∥AB,则AH的长为 ,AE的长为 .
17.用反证法证明“若|a|<2,则a2<4”是真命题,第一步应先假设 .
18.直角三角形的两边长分别是3cm、5cm,则第三边长 cm.
19.若直角三角形的三边分别为3,4,x,则x2= .
20.观察下列等式:32+42=52;52+122=132;72+242=252;92+402=412;112+602=612…按照这样的规律,第六个等式是 .
三.解答题
21.如图,△ABC中,AB=4,∠ABC=45°,D是BC边上一点,且AD=AC,若BD﹣DC=1.求DC的长.
22.如图,在△ABC中,CD⊥AB于点D,AC=20,CD=12,BD=9.求AB与BC的长.
23.如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
24.如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.
(2)计算(1)中线段CD的长.
25.如图,已知BA=BC,BD=BE,∠ABC=∠EBD=90°.
(1)求证:AB平分∠EAC;
(2)若AD=1,CD=3,求BD.
26.用图1中四个完全一样的直角三角形可以拼成图2的大正方形
解答下列问题:
(1)请用含a、b、c的代数式表示大正方形的面积.
方法1 ;方法2 .
(2)根据图2,利用图形的面积关系,推导a、b、c之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且(a+b)2=49,求小正方形的面积.
参考答案与试题解析
一.选择题
1.解:∵Rt△ABC的周长是4+4,斜边上的中线长是2,
∴斜边长为4,
设两个直角边的长为x,y,则x+y=4,x2+y2=16,
解得:xy=8,
∴S△ABC=xy=4.
故选:C.
2.解:∵62+82=102,
∴△ABC是直角三角形,
∴△ABC的面积=×6×8=24.
故选:A.
3.解:∵用反证法证明命题:如果AB∥CD,AB∥EF,那么CD∥EF.
∴证明的第一步应是:从结论反面出发,假设CD不平行于EF.
故选:D.
4.解:∵CA==,
∴AC=AD=,
∴D到原点的距离是﹣2.
∴点D所表示的数是﹣2.
故选:C.
5.解:12+22≠32,故选项A中三条线段不能组成直角三角形;
22+32≠42,故选项B中三条线段不能组成直角三角形;
32+52≠62,故选项C中三条线段不能组成直角三角形;
12+()2=22,故选项D中三条线段能组成直角三角形;
故选:D.
6.解:用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,应先假设两个锐角都大于45°.
故选:A.
7.解:∵|m﹣3|+=0,
∴m﹣3=0且n﹣4=0,
则m=3,n=4,
当4是直角边时,斜边长==5,
当4是斜边时,另一条直角边==,
综上,第三条边长为5或,
故选:C.
8.解:∵直角三角形较短的直角边长是5,小正方形的边长是7,
∴直角三角形的较长直角边=5+7=12,
∴直角三角形斜边长=13,
∴大正方形的边长是13,
∴大正方形的面积是13×13=169.
故选:C.
9.解:∵BC=5,AC==5,
∴S△ABC=×5×3=×AC×BD,
∴BD=3,
解法二:过A点做AE⊥BC交于点E,则易证三角形AEC全等三角形BDC,所以BD等于AE=3.
故选:A.
10.解:(1)1.52+22=2.52,但不是正整数,故错误;
(2)()2+()2=22,能构成直角三角形,但不是整数,故错误;
(3)122+162=202,三边是整数,同时能构成直角三角形,故正确;
(4)0.52+1.22=1.32,但不是正整数,故错误.
故选:A.
二.填空题
11.解:∵∠C=90°,
∴AB2=AC2+BC2,
∴AB2+AC2+BC2=2AB2=2×52=2×25=50.
故答案为:50.
12.解:∵∠A=90°,AC=AB=4,
∴∠ACB=∠ABC=45°,
在Rt△ABC中,BC==4,
CD2+BC2=22+(4)2=36,BD2=62=36,
∴CD2+BC2=BD2,
∴∠BCD=90°,
∴∠ACD=45°,
故答案为:45.
13.解:当第三边是直角边时,根据勾股定理,第三边的长==4,三角形的边长分别为3,4,5能构成三角形;
当第三边是斜边时,根据勾股定理,第三边的长==,三角形的边长分别为3,5,亦能构成三角形;
综合以上两种情况,第三边的长应为4或.
14.解:用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步是假设这个三角形是等腰三角形.
故答案为这个三角形是等腰三角形.
15.解:∵∠C=90°,BC=3,BD=AC=1,
∴CD=2,AD==,AB==,
∴BD+AD=+1,
又∵△ABD中,AD+BD>AB,
∴+1>,
故答案为:<.
16.解:∵四边形ABCD和四边形IJKL是正方形,
∴∠A=∠LIJ=90°,
∵IJ∥AB,
∴∠AEJ=90°,
∴四边形AEJH是矩形,
∴AH=EJ,AE=HJ,
同理,DH=IG,
∵IG=HJ,
∴DH=AE,
∵正方形ABCD的边长为m,正方形IJKL的边长为n,
∴AH+AE=m,AE﹣AH=n,
∴AE=,AH=,
故答案为:,.
17.解:用反证法证明“若|a|<2,则a2<4.”是真命题时,第一步应先假设:a2≥4.
故答案为:a2≥4.
18.解:①当3cm和5cm都是直角边时,第三边为斜边,
由勾股定理得:第三边为=(cm);
②当3cm为直角边和5cm为斜边时,第三边为直角边,
由勾股定理得:第三边为=4(cm).
故答案为:4或.
19.解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理得:
32+42=x2,所以x2=25;
(2)若4是斜边,则第三边x为直角边,由勾股定理得:
32+x2=42,所以x2=7;
故答案为25或7;
20.解:∵第一个等式是:32+42=52;
第二个等式是52+122=132;
第三个等式是72+242=252;
第四个等式是92+402=412;
第五个等式是112+602=612…
按照这样的规律,第六个等式是:132+842=852,
故答案为:132+842=852.
三.解答题
21.解:过点A作AE⊥BC于点E,如图所示.
∵AD=AC,AE⊥BC,
∴∠AEB=90°,DE=CE.
∵∠ABC=45°,
∴∠BAE=45°,
∴AE=BE.
在Rt△ABE中,AB=4,
∴AE2+BE2=AB2,即BE2+BE2=(4)2,
∴BE=4,
∴BD+DC=4.
又∵BD﹣DC=1,
∴DC+1+DC=4,
∴DC=2.
22.解:∵CD⊥AB,AC=20,CD=12,BD=9,
∴∠ADC=∠BDC=90°,
在Rt△CDB中,
由勾股定理得:BC===15,
在Rt△ADC中,
由勾股定理得:AD===16,
∴AB=AD+DB=16+9=25.
答:AB的长为25,BC的长为15.
23.解:连接BD,
在Rt△BAD中,
∵AB=AD=2,
∴∠ADB=45°,BD==2,
在△BCD中,
DB2+CD2=(2)2+12=9=CB2,
∴△BCD是直角三角形,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=45°+90°=135°.
24.解:(1)画角平分线正确,保留画图痕迹
(2)设CD=x,作DE⊥AB于E,
则DE=CD=x,
∵∠C=90°,AC=6,BC=8.
∴AB=10,
∴EB=10﹣6=4.
∵DE2+BE2=DB2,
∴x2+42=(8﹣x)2,
x=3,
即CD长为3.
25.解:(1)证明:∵∠ABC=∠EBD=90°,
∴∠ABD+∠CBD=∠ABD+∠ABE,
∴∠CBD=∠ABE,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴∠EAB=∠BAC,
∴AB平分∠EAC;
(2)∵AD=1,CD=3,
∴AC=4.
∵BA=BC,∠ABC=90°,
∴AB=BC==2,∠C=45°,
过点B作BF⊥AC于点F,如图:
则△BCF为等腰直角三角形,
∴BF=CF=2,
∴DF=CD﹣CF=1,
在Rt△BFD中,由勾股定理得:
BD=
=
=.
∴BD的长等于.
26.解:(1)方法1:大正方形的面积=(a﹣b)2+4×ab=a2+b2,
方法2:大正方形的面积=c2;
故答案为:a2+b2,c2;
(2)因为大正方形的面积相等,
所以a2+b2=c2;
(3)由(2)知,a2+b2=c2.
又(a+b)2=49,
所以 2ab=49﹣(a2+b2)=49﹣c2=49﹣25=24.
所以 小正方形的面积=25﹣24=1.
