2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》同步达标训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》同步达标训练 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:33:06 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》同步达标训练(附答案)
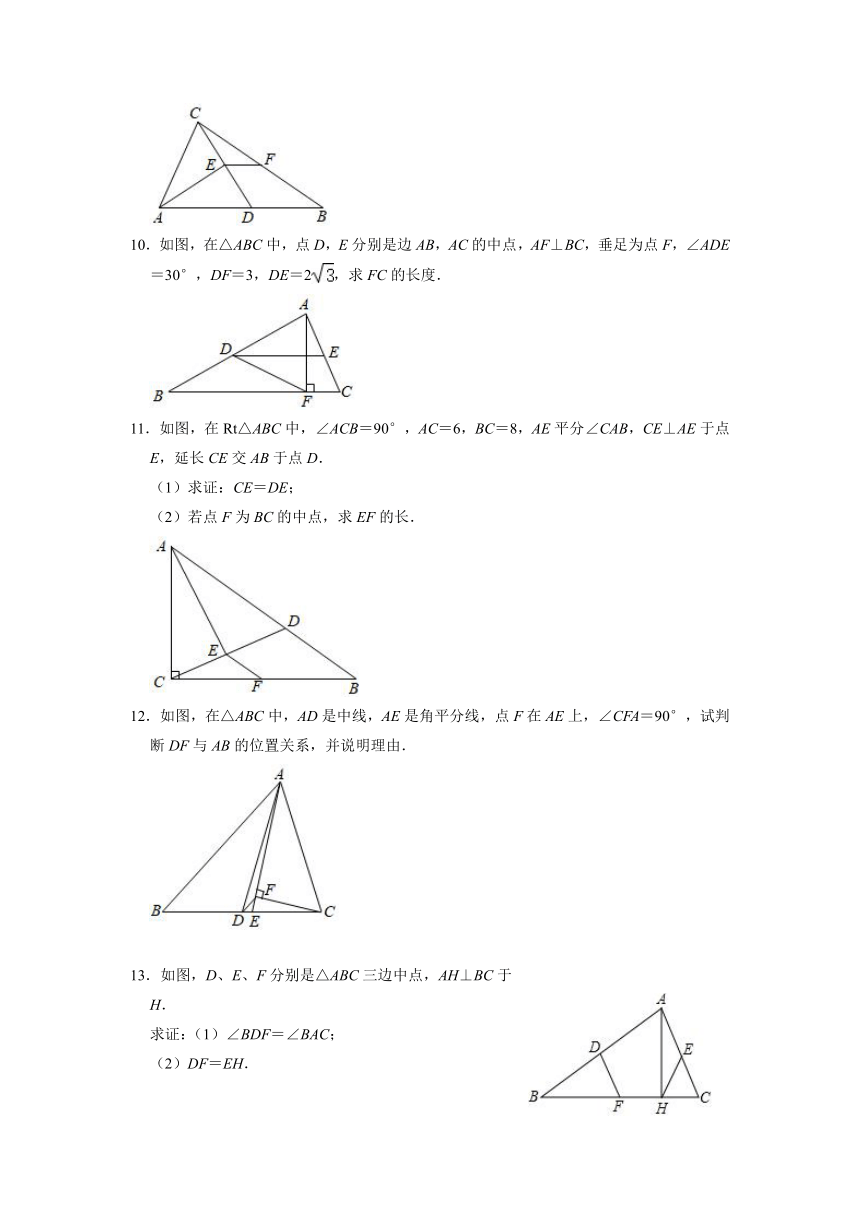
1.如图,四边形ABCD中,AD=BC,点P是对角线BD的中点,E、F分别是AB、CD的中点,若∠EPF=130°,则∠PEF的度数为( )
A.25° B.30° C.35° D.50°
2.如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( )
A.2 B. C. D.
3.如图,在△ABC中,点D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
A.2 B.3 C.6 D.4
4.如图,四边形ABCD中,AD∥BC,AD=2,BC=5,点E,F分别是对角线AC,BD的中点,则EF的长为( )
A.1 B.1.5 C.2.5 D.3.5
5.如图,△ABC的周长为4,点D,E,F分别是AB,BC,CA的中点,则△DEF的周长是( )
A.1 B.2 C.3 D.4
6.如图,已知在△ABC中,D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,则四边形AFDE的周长等于( )
A.18 B.16 C.14 D.12
7.如图所示,在△ABC中,BC>AC,点D在BC上,DC=AC=10,且=,作∠ACB的平分线CF交AD于点F,CF=8,E是AB的中点,连接EF,则EF的长为 .
8.如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长是多少?
9.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=10,求EF的长.
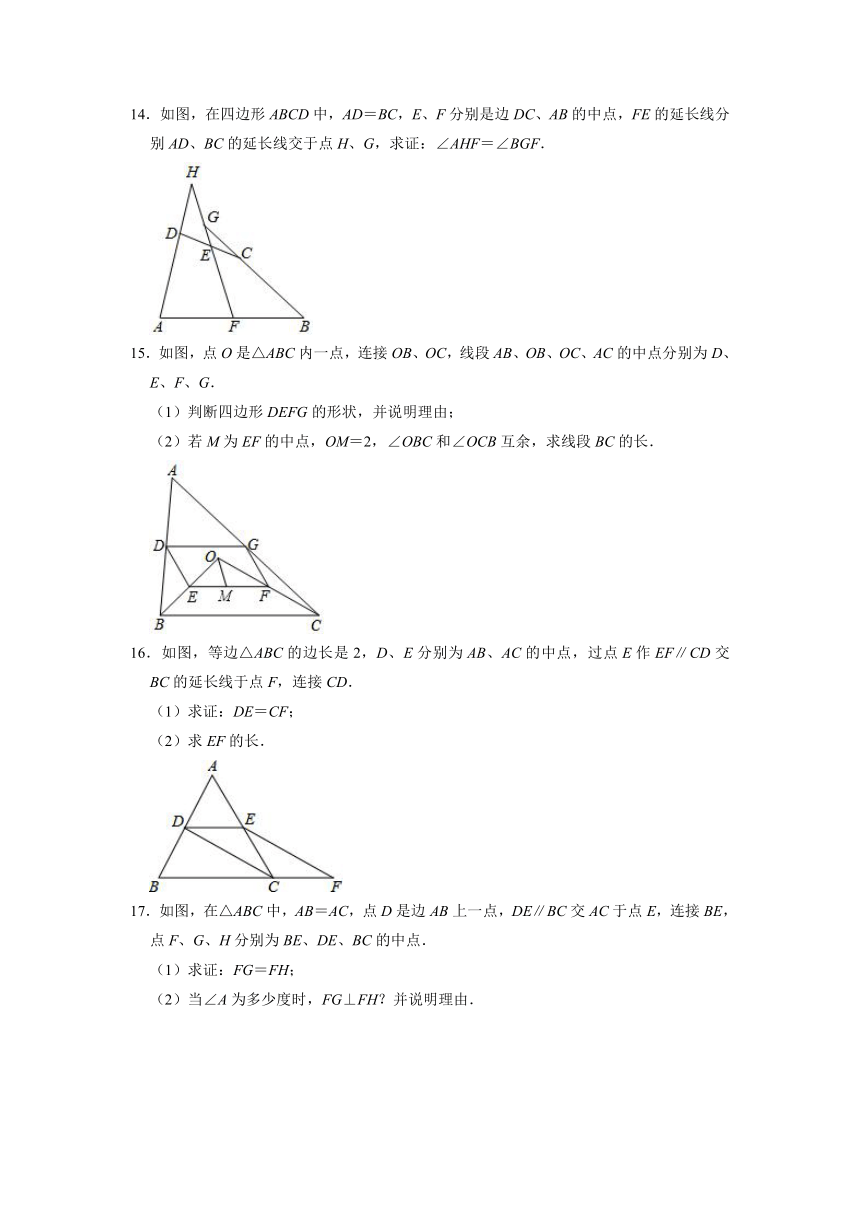
10.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,DE=2,求FC的长度.
11.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.
(1)求证:CE=DE;
(2)若点F为BC的中点,求EF的长.
12.如图,在△ABC中,AD是中线,AE是角平分线,点F在AE上,∠CFA=90°,试判断DF与AB的位置关系,并说明理由.
13.如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.
求证:(1)∠BDF=∠BAC;
(2)DF=EH.
14.如图,在四边形ABCD中,AD=BC,E、F分别是边DC、AB的中点,FE的延长线分别AD、BC的延长线交于点H、G,求证:∠AHF=∠BGF.
15.如图,点O是△ABC内一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G.
(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.
16.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.
(1)求证:DE=CF;
(2)求EF的长.
17.如图,在△ABC中,AB=AC,点D是边AB上一点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
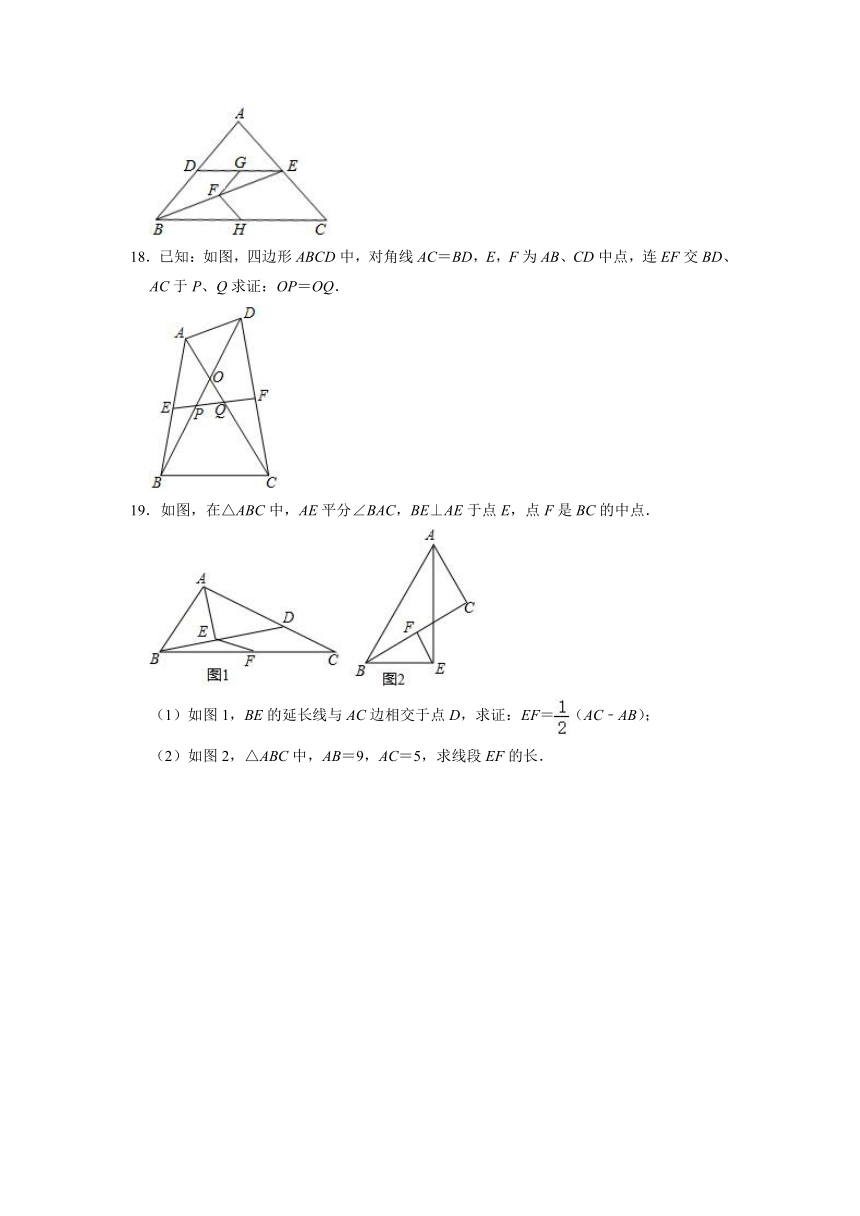
18.已知:如图,四边形ABCD中,对角线AC=BD,E,F为AB、CD中点,连EF交BD、AC于P、Q求证:OP=OQ.
19.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,△ABC中,AB=9,AC=5,求线段EF的长.
参考答案
1.解:∵P、F分别是BD、CD的中点,
∴PF=BC,
同理可得:PE=AD,
∵AD=BC,
∴PF=PE,
∵∠EPF=130°,
∴∠PEF=∠PFE=×(180°﹣130°)=25°,
故选:A.
2.解:取BC的中点G,AD的中点H,连接EG、GF、FH、HE,
∵E,G分别是AB,BC的中点,AC=2
∴EG=AC=1,EG∥AC,
同理:FH=AC,FH∥AC,EG=AC,GF∥BD,GF=BD=1,
∴四边形EGFH为平行四边形,
∵AC=BD,
∴GE=GF,
∴平行四边形EGFH为菱形,
∵AC⊥BD,EG∥AC,GF∥BD,
∴EG⊥GF,
∴菱形EGFH为正方形,
∴EF=EG=,
故选:D.
3.解:∵D,E分别是BC,AC的中点,
∴DE∥AB,
∴∠BFD=∠ABF,
∵BF平分∠ABC,
∴∠DBF=∠ABF,
∴∠BFD=∠DBF,
∴DF=DB=BC==3,
故选:B.
4.解:∵取DC中点G,连结FG、EG,如图所示:
∵点E,F分别是对角线AC,BD的中点,
∴FG∥BC,EG∥AD,
∵AD∥BC,
∴EG∥BC,FG∥EG,
∴E、F、G三点共线,
∴FG是△BCD的中位线,
∴FG=BC=2.5,
∵AD∥BC,
∴EG∥AD,
∴EG是△ACD的中位线,
∴EG=AD=1,
∴EF=FG﹣EG=1.5.
故选:B.
5.解:∵△ABC的周长为4,
∴AB+AC+BC=4,
∵点D,E,F分别是AB,BC,CA的中点,
∴EF=AB,DE=AC,DF=BC,
∴△DEF的周长=EF+DE+DF=×(AB+AC+BC)=2,
故选:B.
6.解:∵D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,
∴DE=AB=5,DF=AC=4,AF=AB=5,AE=AC=4,
∴四边形AFDE的周长=AF+DF+DE+AE=5+5+4+4=18,
故选:A.
7.解:∵DC=AC=10,∠ACB的平分线CF交AD于F,
∴F为AD的中点,CF⊥AD,
∴∠CFD=90°,
∵DC=10,CF=8,
∴DF==6,
∴AD=2DF=12,
∵=,
∴BD=8,
∵点E是AB的中点,
∴EF为△ABD的中位线,
∴EF=BD=4,
故答案为:4.
8.解:∵M,N分别是AB和AC的中点,
∴MN是△ABC的中位线,
∴MN=BC=2,MN∥BC,
∴∠NME=∠D,∠MNE=∠DCE,
∵点E是CN的中点,
∴NE=CE,
在△MNE和△DCE中,
,
∴△MNE≌△DCE(AAS),
∴CD=MN=2.
9.解:∵AD=AC,AE⊥CD,
∴CE=ED,
∵F是BC的中点,
∴EF是△CDB的中位线,
∴EF=BD=×10=5.
10.解:∵AF⊥BC,点D是边AB的中点,DF=3,
∴AB=2DF=6.
∵点D,E分别是边AB,AC的中点,
∴DE∥BC,
∴∠B=∠ADE=30°,
∴AF=AB=3,
由勾股定理得,BF===3,
∴FC=BC﹣BF=.
11.(1)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵CE⊥AE,
∴∠AEC=∠AED=90°,
在△AEC和△AED中,
,
∴△AEC≌△AED(ASA),
∴CE=DE;
(2)在Rt△ABC中,∵AC=6,BC=8,
∴,
∵△AEC≌△AED,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵点E为CD中点,点F为BC中点,
∴.
12.解:DF∥AB.理由如下:
如图,延长CF交AB于点G,
∵AE是角平分线,
∴∠GAF=∠CAF,
在△AGF和△ACF中,
∴△AGF≌△ACF(ASA),
∴GF=CF,
即点F是GC的中点,
∵AD是△ABC的中线,
∴点D是BC的中点
∴DF是△BCG的中位线,
∴DF∥AB.
13.证明:(1)∵D、F分别是AB、BC边中点,
∴DF是△ABC的中位线,
∴DF∥AC,DF=AC,
∴∠BDF=∠BAC;
(2)∵AH⊥BC于H,E是AC的中点,
∴EH=AC,
∴DF=EH.
14.证明:连接BD,取BD的中点P,连接EP,FP,
∵E、F、P分别是DC、AB、BD边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF.
15.解:(1)四边形DEFG是平行四边形,
理由如下:∵E、F分别为线段OB、OC的中点,
∴EF=BC,EF∥BC,
同理DG=BC,DG∥BC,
∴EF=DG,EF∥DG,
∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,
∴∠BOC=90°,
∵M为EF的中点,OM=2,
∴EF=2OM=4,
∴BC=2EF=8.
16.解:(1)∵D、E分别为AB、AC的中点,
∴DE∥BC,DE=BC,
∵EF∥CD
∴四边形DEFC是平行四边形,
∴DE=CF.
(2)∵四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF=.
17.(1)证明:∵AB=AC.
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=BD,FH=CE,
∴FG=FH;
(2)解:延长FG交AC于N,
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.
18.证明:取BC中点G,连EG、FG,
∵E,G为AB、BC中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP,
同理,FG=BD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
19.(1)证明:在△AEB和△AED中,
,
∴△AEB≌△AED(ASA)
∴BE=ED,AD=AB,
∵BE=ED,BF=FC,
∴EF=CD=(AC﹣AD)=(AC﹣AB);
(2)解:分别延长BE、AC交于点H,
在△AEB和△AEH中,
,
∴△AEB≌△AEH(ASA)
∴BE=EH,AH=AB=9,
∵BE=EH,BF=FC,
∴EF=CH=(AH﹣AC)=2.
1.如图,四边形ABCD中,AD=BC,点P是对角线BD的中点,E、F分别是AB、CD的中点,若∠EPF=130°,则∠PEF的度数为( )
A.25° B.30° C.35° D.50°
2.如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( )
A.2 B. C. D.
3.如图,在△ABC中,点D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
A.2 B.3 C.6 D.4
4.如图,四边形ABCD中,AD∥BC,AD=2,BC=5,点E,F分别是对角线AC,BD的中点,则EF的长为( )
A.1 B.1.5 C.2.5 D.3.5
5.如图,△ABC的周长为4,点D,E,F分别是AB,BC,CA的中点,则△DEF的周长是( )
A.1 B.2 C.3 D.4
6.如图,已知在△ABC中,D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,则四边形AFDE的周长等于( )
A.18 B.16 C.14 D.12
7.如图所示,在△ABC中,BC>AC,点D在BC上,DC=AC=10,且=,作∠ACB的平分线CF交AD于点F,CF=8,E是AB的中点,连接EF,则EF的长为 .
8.如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长是多少?
9.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=10,求EF的长.
10.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,DE=2,求FC的长度.
11.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.
(1)求证:CE=DE;
(2)若点F为BC的中点,求EF的长.
12.如图,在△ABC中,AD是中线,AE是角平分线,点F在AE上,∠CFA=90°,试判断DF与AB的位置关系,并说明理由.
13.如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.
求证:(1)∠BDF=∠BAC;
(2)DF=EH.
14.如图,在四边形ABCD中,AD=BC,E、F分别是边DC、AB的中点,FE的延长线分别AD、BC的延长线交于点H、G,求证:∠AHF=∠BGF.
15.如图,点O是△ABC内一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G.
(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.
16.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.
(1)求证:DE=CF;
(2)求EF的长.
17.如图,在△ABC中,AB=AC,点D是边AB上一点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
18.已知:如图,四边形ABCD中,对角线AC=BD,E,F为AB、CD中点,连EF交BD、AC于P、Q求证:OP=OQ.
19.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,△ABC中,AB=9,AC=5,求线段EF的长.
参考答案
1.解:∵P、F分别是BD、CD的中点,
∴PF=BC,
同理可得:PE=AD,
∵AD=BC,
∴PF=PE,
∵∠EPF=130°,
∴∠PEF=∠PFE=×(180°﹣130°)=25°,
故选:A.
2.解:取BC的中点G,AD的中点H,连接EG、GF、FH、HE,
∵E,G分别是AB,BC的中点,AC=2
∴EG=AC=1,EG∥AC,
同理:FH=AC,FH∥AC,EG=AC,GF∥BD,GF=BD=1,
∴四边形EGFH为平行四边形,
∵AC=BD,
∴GE=GF,
∴平行四边形EGFH为菱形,
∵AC⊥BD,EG∥AC,GF∥BD,
∴EG⊥GF,
∴菱形EGFH为正方形,
∴EF=EG=,
故选:D.
3.解:∵D,E分别是BC,AC的中点,
∴DE∥AB,
∴∠BFD=∠ABF,
∵BF平分∠ABC,
∴∠DBF=∠ABF,
∴∠BFD=∠DBF,
∴DF=DB=BC==3,
故选:B.
4.解:∵取DC中点G,连结FG、EG,如图所示:
∵点E,F分别是对角线AC,BD的中点,
∴FG∥BC,EG∥AD,
∵AD∥BC,
∴EG∥BC,FG∥EG,
∴E、F、G三点共线,
∴FG是△BCD的中位线,
∴FG=BC=2.5,
∵AD∥BC,
∴EG∥AD,
∴EG是△ACD的中位线,
∴EG=AD=1,
∴EF=FG﹣EG=1.5.
故选:B.
5.解:∵△ABC的周长为4,
∴AB+AC+BC=4,
∵点D,E,F分别是AB,BC,CA的中点,
∴EF=AB,DE=AC,DF=BC,
∴△DEF的周长=EF+DE+DF=×(AB+AC+BC)=2,
故选:B.
6.解:∵D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,
∴DE=AB=5,DF=AC=4,AF=AB=5,AE=AC=4,
∴四边形AFDE的周长=AF+DF+DE+AE=5+5+4+4=18,
故选:A.
7.解:∵DC=AC=10,∠ACB的平分线CF交AD于F,
∴F为AD的中点,CF⊥AD,
∴∠CFD=90°,
∵DC=10,CF=8,
∴DF==6,
∴AD=2DF=12,
∵=,
∴BD=8,
∵点E是AB的中点,
∴EF为△ABD的中位线,
∴EF=BD=4,
故答案为:4.
8.解:∵M,N分别是AB和AC的中点,
∴MN是△ABC的中位线,
∴MN=BC=2,MN∥BC,
∴∠NME=∠D,∠MNE=∠DCE,
∵点E是CN的中点,
∴NE=CE,
在△MNE和△DCE中,
,
∴△MNE≌△DCE(AAS),
∴CD=MN=2.
9.解:∵AD=AC,AE⊥CD,
∴CE=ED,
∵F是BC的中点,
∴EF是△CDB的中位线,
∴EF=BD=×10=5.
10.解:∵AF⊥BC,点D是边AB的中点,DF=3,
∴AB=2DF=6.
∵点D,E分别是边AB,AC的中点,
∴DE∥BC,
∴∠B=∠ADE=30°,
∴AF=AB=3,
由勾股定理得,BF===3,
∴FC=BC﹣BF=.
11.(1)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵CE⊥AE,
∴∠AEC=∠AED=90°,
在△AEC和△AED中,
,
∴△AEC≌△AED(ASA),
∴CE=DE;
(2)在Rt△ABC中,∵AC=6,BC=8,
∴,
∵△AEC≌△AED,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵点E为CD中点,点F为BC中点,
∴.
12.解:DF∥AB.理由如下:
如图,延长CF交AB于点G,
∵AE是角平分线,
∴∠GAF=∠CAF,
在△AGF和△ACF中,
∴△AGF≌△ACF(ASA),
∴GF=CF,
即点F是GC的中点,
∵AD是△ABC的中线,
∴点D是BC的中点
∴DF是△BCG的中位线,
∴DF∥AB.
13.证明:(1)∵D、F分别是AB、BC边中点,
∴DF是△ABC的中位线,
∴DF∥AC,DF=AC,
∴∠BDF=∠BAC;
(2)∵AH⊥BC于H,E是AC的中点,
∴EH=AC,
∴DF=EH.
14.证明:连接BD,取BD的中点P,连接EP,FP,
∵E、F、P分别是DC、AB、BD边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF.
15.解:(1)四边形DEFG是平行四边形,
理由如下:∵E、F分别为线段OB、OC的中点,
∴EF=BC,EF∥BC,
同理DG=BC,DG∥BC,
∴EF=DG,EF∥DG,
∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,
∴∠BOC=90°,
∵M为EF的中点,OM=2,
∴EF=2OM=4,
∴BC=2EF=8.
16.解:(1)∵D、E分别为AB、AC的中点,
∴DE∥BC,DE=BC,
∵EF∥CD
∴四边形DEFC是平行四边形,
∴DE=CF.
(2)∵四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF=.
17.(1)证明:∵AB=AC.
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=BD,FH=CE,
∴FG=FH;
(2)解:延长FG交AC于N,
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.
18.证明:取BC中点G,连EG、FG,
∵E,G为AB、BC中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP,
同理,FG=BD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
19.(1)证明:在△AEB和△AED中,
,
∴△AEB≌△AED(ASA)
∴BE=ED,AD=AB,
∵BE=ED,BF=FC,
∴EF=CD=(AC﹣AD)=(AC﹣AB);
(2)解:分别延长BE、AC交于点H,
在△AEB和△AEH中,
,
∴△AEB≌△AEH(ASA)
∴BE=EH,AH=AB=9,
∵BE=EH,BF=FC,
∴EF=CH=(AH﹣AC)=2.
