2021-2022学年苏科版九年级数学下册《7.5解直角三角形》同步达标训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册《7.5解直角三角形》同步达标训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 413.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:34:56 | ||
图片预览



文档简介
2021-2022学年苏科版九年级数学下册《7.5解直角三角形》同步达标训练(附答案)
1.如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.2 B.4 C.5 D.10
2.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
3.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为( )
A.7 B.8 C.8或17 D.7或17
4.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
5.如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
A.x﹣y2=3 B.2x﹣y2=9 C.3x﹣y2=15 D.4x﹣y2=21
6.如图,在△ABC中,AD⊥BC,垂足为点D,若AC=6,∠C=45°,tan∠ABC=3,则BD等于( )
A.2 B.3 C.3 D.2
7.如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
A. B. C. D.
8.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
A.10 B.8 C.4 D.2
9.如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB的长为 .
10.如图,在菱形ABCD中,AE⊥BC,E为垂足,若cosB=,EC=2,P是AB边上的一个动点,则线段PE的长度的最小值是 .
11.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是 .
12.BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD=,则CD的长为 .
13.如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
(2)sin∠ADC的值.
14.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.
15.如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=,求BE的值.
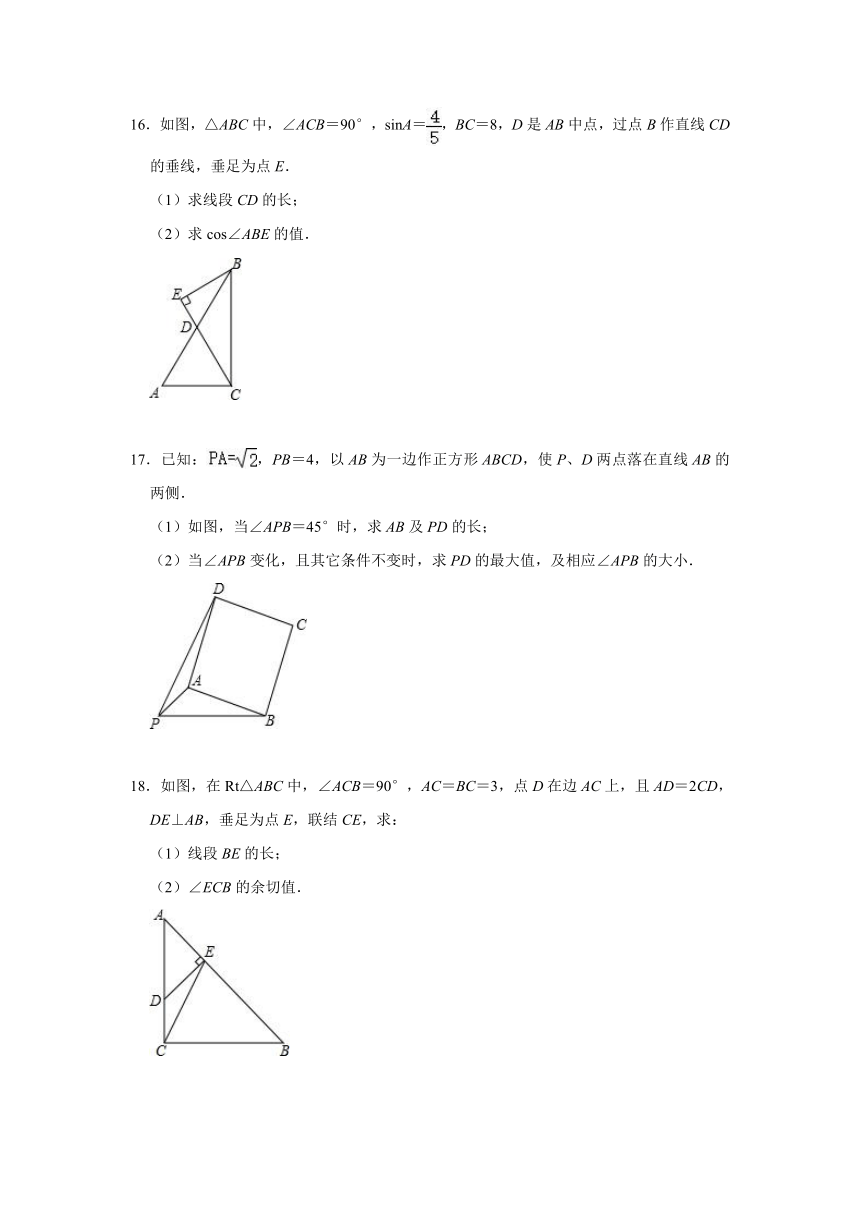
16.如图,△ABC中,∠ACB=90°,sinA=,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
17.已知:,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
18.如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求:
(1)线段BE的长;
(2)∠ECB的余切值.
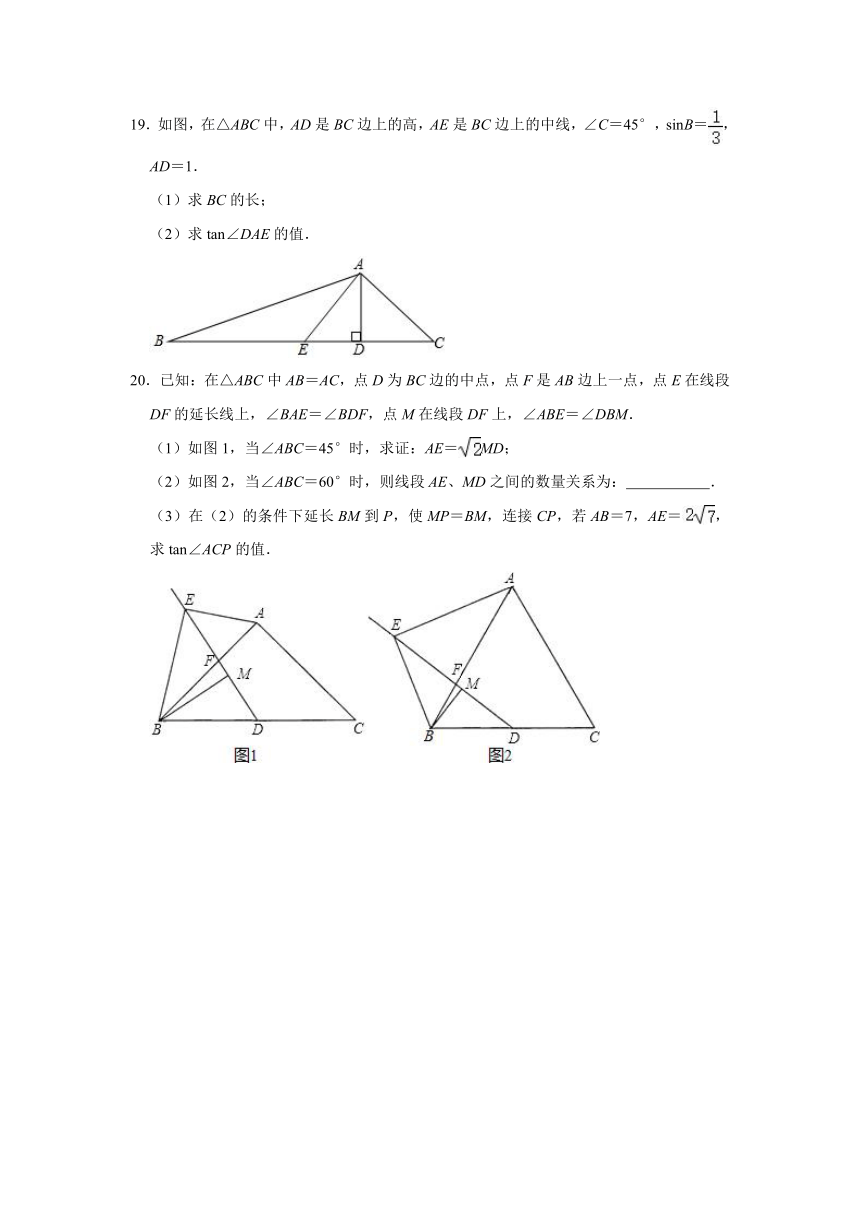
19.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
20.已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
(1)如图1,当∠ABC=45°时,求证:AE=MD;
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为: .
(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=,求tan∠ACP的值.
参考答案
1.解:如图,作DH⊥AB于H,CM⊥AB于M.
∵BE⊥AC,
∴∠AEB=90°,
∵tanA==2,设AE=a,BE=2a,
则有:100=a2+4a2,
∴a2=20,
∴a=2或﹣2(舍弃),
∴BE=2a=4,
∵AB=AC,BE⊥AC,CM⊥AB,
∴CM=BE=4(等腰三角形两腰上的高相等),
∵∠DBH=∠ABE,∠BHD=∠BEA,
∴sin∠DBH===,
∴DH=BD,
∴CD+BD=CD+DH,
∴CD+DH≥CM,
∴CD+BD≥4,
∴CD+BD的最小值为4.
方法二:作CM⊥AB于M,交BE于点D,则点D满足题意.通过三角形相似或三角函数证得BD=DM,从而得到CD+BD=CM=4.
故选:B.
2.解:如图,∵在△ABC中,AC⊥BC,∠ABC=30°,
∴AB=2AC,BC==AC.
∵BD=BA,
∴DC=BD+BC=(2+)AC,
∴tan∠DAC===2+.
故选:A.
3.解:∵cos∠B=,
∴∠B=45°,
当△ABC为钝角三角形时,如图1,
∵AB=12,∠B=45°,
∴AD=BD=12,
∵AC=13,
∴由勾股定理得CD=5,
∴BC=BD﹣CD=12﹣5=7;
当△ABC为锐角三角形时,如图2,
BC=BD+CD=12+5=17,
故选:D.
4.解:∵AD∥BC,∠DAB=90°,
∴∠ABC=180°﹣∠DAB=90°,∠BAC+∠EAD=90°,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADB+∠EAD=90°,
∴∠BAC=∠ADB,
∴△ABC∽△DAB,
∴=,
∵BC=AD,
∴AD=2BC,
∴AB2=BC×AD=BC×2BC=2BC2,
∴AB=BC,
在Rt△ABC中,tan∠BAC===;
故选:C.
5.解:
过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE,
∵BE的垂直平分线交BC于D,BD=x,
∴BD=DE=x,
∵AB=AC,BC=12,tan∠ACB=y,
∴==y,BQ=CQ=6,
∴AQ=6y,
∵AQ⊥BC,EM⊥BC,
∴AQ∥EM,
∵E为AC中点,
∴CM=QM=CQ=3,
∴EM=3y,
∴DM=12﹣3﹣x=9﹣x,
在Rt△EDM中,由勾股定理得:x2=(3y)2+(9﹣x)2,
即2x﹣y2=9,
故选:B.
6.解:∵AC=6,∠C=45°,
∴AD=AC sin45°=6×=6,
∵tan∠ABC=3,
∴=3,
∴BD==2,
故选:A.
7.解:∵△ABC中,AB=AC=4,∠C=72°,
∴∠ABC=∠C=72°,∠A=36°,
∵D是AB中点,DE⊥AB,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC﹣∠ABE=36°,
∠BEC=180°﹣∠EBC﹣∠C=72°,
∴∠BEC=∠C=72°,
∴BE=BC,
∴AE=BE=BC.
设AE=x,则BE=BC=x,EC=4﹣x.
在△BCE与△ABC中,
,
∴△BCE∽△ABC,
∴=,即=,
解得x=﹣2±2(负值舍去),
∴AE=﹣2+2.
在△ADE中,∵∠ADE=90°,
∴cosA===.
故选:C.
8.解:∵∠C=90°,cos∠BDC=,
设CD=5x,BD=7x,
∴BC=2x,
∵AB的垂直平分线EF交AC于点D,
∴AD=BD=7x,
∴AC=12x,
∵AC=12,
∴x=1,
∴BC=2;
故选:D.
9.解:过C作CD⊥AB于D,
∴∠ADC=∠BDC=90°,
∵∠B=45°,
∴∠BCD=∠B=45°,
∴CD=BD,
∵∠A=30°,AC=2,
∴CD=,
∴BD=CD=,
由勾股定理得:AD==3,
∴AB=AD+BD=3+.
故答案为:3+.
10.解:设菱形ABCD的边长为x,则AB=BC=x,又EC=2,所以BE=x﹣2,
因为AE⊥BC于E,
所以在Rt△ABE中,cosB=,又cosB=,
于是,
解得x=10,即AB=10.
所以易求BE=8,AE=6,
当EP⊥AB时,PE取得最小值.
故由三角形面积公式有:AB PE=BE AE,
求得PE的最小值为4.8.
故答案为 4.8.
11.解:在Rt△ABC与Rt△BCD中,∠A+∠B=90°,∠BCD+∠B=90°.
∴∠A=∠BCD.
∴tan∠BCD=tan∠A===.
故答案为.
12.解:分三种情况:
①如图1,∠A为钝角,AB=AC,
在Rt△ABD中,∵BD=1,tan∠ABD=,
∴AD=,AB=2,
∴AC=2,
∴CD=2+,
②如图2,∠A为锐角,AB=AC,
在Rt△ABD中,∵BD=1,tan∠ABD=,
∴AD=,AB=2,
∴AC=2,
∴CD=2﹣,
③如图3,∠A为底角,
∵tan∠ABD=,
∴∠ABD=60°,
∴∠A=30°,
∴∠C=120°,
∴∠BCD=60°
∵BD=1,
∴CD=;
④∠C为锐角且为顶角时,
如图4,∵BD⊥AC,
∴∠ADB=90°,
∵tan∠ABD=,
∴∠ABD=60°,
∴∠A=30°,
∵∠CBA=∠A=30°,∴∠C=120°>90°,
∴这种情况不存在;
综上所述;CD的长为:2或2﹣或,
故答案为:2或2﹣或.
13.解:(1)过点A作AE⊥BC于点E,
∵cosC=,
∴∠C=45°,
在Rt△ACE中,CE=AC cosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=,即=,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴CD=BC=2,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=.
14.解:∵在直角△ABD中,tan∠BAD==,
∴BD=AD tan∠BAD=12×=9,
∴CD=BC﹣BD=14﹣9=5,
∴AC===13,
∴sinC==.
15.解:(1)∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∠ACB=90°
∴∠BCD+∠ACH=90°
∴∠B=∠BCD=∠CAH,即∠B=∠CAH,
∵AH=2CH,
∴由勾股定理得AC=CH,
∴CH:AC=1:,
∴sinB=;
(2)∵sinB=,
∴AC:AB=1:,
∴AC=2.
∵∠CAH=∠B,
∴sin∠CAH=sinB==,
设CE=x(x>0),则AE=x,则x2+22=(x)2,
∴CE=x=1,AC=2,
在Rt△ABC中,AC2+BC2=AB2,
∵AB=2CD=2,
∴BC=4,
∴BE=BC﹣CE=3.
16.解:(1)在△ABC中,∵∠ACB=90°,
∴sinA==,
而BC=8,
∴AB=10,
∵D是AB中点,
∴CD=AB=5;
(2)在Rt△ABC中,∵AB=10,BC=8,
∴AC==6,
∵D是AB中点,
∴BD=5,S△BDC=S△ADC,
∴S△BDC=S△ABC,即CD BE= AC BC,
∴BE==,
在Rt△BDE中,cos∠DBE===,
即cos∠ABE的值为.
17.解:(1)①如图,作AE⊥PB于点E,
∵△APE中,∠APE=45°,PA=,
∴AE=PE=×=1,
∵PB=4,∴BE=PB﹣PE=3,
在Rt△ABE中,∠AEB=90°,
∴AB==.
②解法一:如图,因为四边形ABCD为正方形,可将
△PAD绕点A顺时针旋转90°得到△P'AB,
可得△PAD≌△P'AB,PD=P'B,PA=P'A.
∴∠PAP'=90°,∠APP'=45°,∠P'PB=90°
∴PP′=PA=2,
∴PD=P′B===;
解法二:如图,过点P作AB的平行线,与DA的延长线交于F,与DA的
延长线交PB于G.
在Rt△AEG中,
可得AG===,EG=,PG=PE﹣EG=.
在Rt△PFG中,
可得PF=PG cos∠FPG=PG cos∠ABE=,FG=.
在Rt△PDF中,可得,
PD===.
(2)如图所示,
将△PAD绕点A顺时针旋转90°
得到△P'AB,PD的最大值即为P'B的最大值,
∵△P'PB中,P'B<PP'+PB,PP′=PA=2,PB=4,
且P、D两点落在直线AB的两侧,
∴当P'、P、B三点共线时,P'B取得最大值(如图)
此时P'B=PP'+PB=6,即P'B的最大值为6.
此时∠APB=180°﹣∠APP'=135度.
18.解:(1)∵AD=2CD,AC=3,
∴AD=2,
∵在Rt△ABC中,∠ACB=90°,AC=BC=3,
∴∠A=∠B=45°,AB===3,
∵DE⊥AB,
∴∠AED=90°,∠ADE=∠A=45°,
∴AE=AD cos45°=2×=,
∴BE=AB﹣AE=3﹣=2,
即线段BE的长为2;
(2)过点E作EH⊥BC,垂足为点H,如图所示:
∵在Rt△BEH中,∠EHB=90°,∠B=45°,
∴EH=BH=BE cos45°=2×=2,
∵BC=3,
∴CH=1,
在Rt△CHE中,cot∠ECB==,
即∠ECB的余切值为.
19.解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=,AD=1,
∴AB==3,
∴BD==2,
∴BC=BD+DC=2+1;
(2)∵AE是BC边上的中线,
∴CE=BC=+,
∴DE=CE﹣CD=﹣,
∴tan∠DAE==﹣.
20.(1)证明:如图1,连接AD.
∵AB=AC,BD=CD,
∴AD⊥BC.
又∵∠ABC=45°,
∴BD=AB cos∠ABC即AB=BD.
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM.
∴,
∴AE=MD.
(2)解:∵cos60°=,
∴MD=AE cos∠ABC=AE ,即AE=2MD.
∴AE=2MD;
(3)解:如图2,连接AD,EP.
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形.
又∵D为BC的中点,
∴AD⊥BC,∠DAC=30°,BD=DC=AB.
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM.
∴,
∠AEB=∠DMB.
∴EB=2BM.
又∵BM=MP,
∴EB=BP.
∵∠EBM=∠ABC=60°,
∴△BEP为等边三角形,
∴EM⊥BP,
∴∠BMD=90°,
∴∠AEB=90°.
在Rt△AEB中,AE=2,AB=7,
∴BE=.
∴tan∠EAB=.
∵D为BC中点,M为BP中点,
∴DM∥PC.
∴∠MDB=∠PCB,
∴∠EAB=∠PCB.
∴tan∠PCB=.
在Rt△ABD中,AD=AB sin∠ABD=,
在Rt△NDC中,ND=DC tan∠NCD=,
∴NA=AD﹣ND=.
过N作NH⊥AC,垂足为H.
在Rt△ANH中,NH=AN=,AH=AN cos∠NAH=,
∴CH=AC﹣AH=,
∴tan∠ACP=.
1.如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.2 B.4 C.5 D.10
2.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
A.2+ B.2 C.3+ D.3
3.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为( )
A.7 B.8 C.8或17 D.7或17
4.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是( )
A. B. C. D.
5.如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
A.x﹣y2=3 B.2x﹣y2=9 C.3x﹣y2=15 D.4x﹣y2=21
6.如图,在△ABC中,AD⊥BC,垂足为点D,若AC=6,∠C=45°,tan∠ABC=3,则BD等于( )
A.2 B.3 C.3 D.2
7.如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
A. B. C. D.
8.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
A.10 B.8 C.4 D.2
9.如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB的长为 .
10.如图,在菱形ABCD中,AE⊥BC,E为垂足,若cosB=,EC=2,P是AB边上的一个动点,则线段PE的长度的最小值是 .
11.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是 .
12.BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD=,则CD的长为 .
13.如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
(2)sin∠ADC的值.
14.如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.
15.如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=,求BE的值.
16.如图,△ABC中,∠ACB=90°,sinA=,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
17.已知:,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
18.如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求:
(1)线段BE的长;
(2)∠ECB的余切值.
19.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
20.已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
(1)如图1,当∠ABC=45°时,求证:AE=MD;
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为: .
(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=,求tan∠ACP的值.
参考答案
1.解:如图,作DH⊥AB于H,CM⊥AB于M.
∵BE⊥AC,
∴∠AEB=90°,
∵tanA==2,设AE=a,BE=2a,
则有:100=a2+4a2,
∴a2=20,
∴a=2或﹣2(舍弃),
∴BE=2a=4,
∵AB=AC,BE⊥AC,CM⊥AB,
∴CM=BE=4(等腰三角形两腰上的高相等),
∵∠DBH=∠ABE,∠BHD=∠BEA,
∴sin∠DBH===,
∴DH=BD,
∴CD+BD=CD+DH,
∴CD+DH≥CM,
∴CD+BD≥4,
∴CD+BD的最小值为4.
方法二:作CM⊥AB于M,交BE于点D,则点D满足题意.通过三角形相似或三角函数证得BD=DM,从而得到CD+BD=CM=4.
故选:B.
2.解:如图,∵在△ABC中,AC⊥BC,∠ABC=30°,
∴AB=2AC,BC==AC.
∵BD=BA,
∴DC=BD+BC=(2+)AC,
∴tan∠DAC===2+.
故选:A.
3.解:∵cos∠B=,
∴∠B=45°,
当△ABC为钝角三角形时,如图1,
∵AB=12,∠B=45°,
∴AD=BD=12,
∵AC=13,
∴由勾股定理得CD=5,
∴BC=BD﹣CD=12﹣5=7;
当△ABC为锐角三角形时,如图2,
BC=BD+CD=12+5=17,
故选:D.
4.解:∵AD∥BC,∠DAB=90°,
∴∠ABC=180°﹣∠DAB=90°,∠BAC+∠EAD=90°,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADB+∠EAD=90°,
∴∠BAC=∠ADB,
∴△ABC∽△DAB,
∴=,
∵BC=AD,
∴AD=2BC,
∴AB2=BC×AD=BC×2BC=2BC2,
∴AB=BC,
在Rt△ABC中,tan∠BAC===;
故选:C.
5.解:
过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE,
∵BE的垂直平分线交BC于D,BD=x,
∴BD=DE=x,
∵AB=AC,BC=12,tan∠ACB=y,
∴==y,BQ=CQ=6,
∴AQ=6y,
∵AQ⊥BC,EM⊥BC,
∴AQ∥EM,
∵E为AC中点,
∴CM=QM=CQ=3,
∴EM=3y,
∴DM=12﹣3﹣x=9﹣x,
在Rt△EDM中,由勾股定理得:x2=(3y)2+(9﹣x)2,
即2x﹣y2=9,
故选:B.
6.解:∵AC=6,∠C=45°,
∴AD=AC sin45°=6×=6,
∵tan∠ABC=3,
∴=3,
∴BD==2,
故选:A.
7.解:∵△ABC中,AB=AC=4,∠C=72°,
∴∠ABC=∠C=72°,∠A=36°,
∵D是AB中点,DE⊥AB,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC﹣∠ABE=36°,
∠BEC=180°﹣∠EBC﹣∠C=72°,
∴∠BEC=∠C=72°,
∴BE=BC,
∴AE=BE=BC.
设AE=x,则BE=BC=x,EC=4﹣x.
在△BCE与△ABC中,
,
∴△BCE∽△ABC,
∴=,即=,
解得x=﹣2±2(负值舍去),
∴AE=﹣2+2.
在△ADE中,∵∠ADE=90°,
∴cosA===.
故选:C.
8.解:∵∠C=90°,cos∠BDC=,
设CD=5x,BD=7x,
∴BC=2x,
∵AB的垂直平分线EF交AC于点D,
∴AD=BD=7x,
∴AC=12x,
∵AC=12,
∴x=1,
∴BC=2;
故选:D.
9.解:过C作CD⊥AB于D,
∴∠ADC=∠BDC=90°,
∵∠B=45°,
∴∠BCD=∠B=45°,
∴CD=BD,
∵∠A=30°,AC=2,
∴CD=,
∴BD=CD=,
由勾股定理得:AD==3,
∴AB=AD+BD=3+.
故答案为:3+.
10.解:设菱形ABCD的边长为x,则AB=BC=x,又EC=2,所以BE=x﹣2,
因为AE⊥BC于E,
所以在Rt△ABE中,cosB=,又cosB=,
于是,
解得x=10,即AB=10.
所以易求BE=8,AE=6,
当EP⊥AB时,PE取得最小值.
故由三角形面积公式有:AB PE=BE AE,
求得PE的最小值为4.8.
故答案为 4.8.
11.解:在Rt△ABC与Rt△BCD中,∠A+∠B=90°,∠BCD+∠B=90°.
∴∠A=∠BCD.
∴tan∠BCD=tan∠A===.
故答案为.
12.解:分三种情况:
①如图1,∠A为钝角,AB=AC,
在Rt△ABD中,∵BD=1,tan∠ABD=,
∴AD=,AB=2,
∴AC=2,
∴CD=2+,
②如图2,∠A为锐角,AB=AC,
在Rt△ABD中,∵BD=1,tan∠ABD=,
∴AD=,AB=2,
∴AC=2,
∴CD=2﹣,
③如图3,∠A为底角,
∵tan∠ABD=,
∴∠ABD=60°,
∴∠A=30°,
∴∠C=120°,
∴∠BCD=60°
∵BD=1,
∴CD=;
④∠C为锐角且为顶角时,
如图4,∵BD⊥AC,
∴∠ADB=90°,
∵tan∠ABD=,
∴∠ABD=60°,
∴∠A=30°,
∵∠CBA=∠A=30°,∴∠C=120°>90°,
∴这种情况不存在;
综上所述;CD的长为:2或2﹣或,
故答案为:2或2﹣或.
13.解:(1)过点A作AE⊥BC于点E,
∵cosC=,
∴∠C=45°,
在Rt△ACE中,CE=AC cosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=,即=,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴CD=BC=2,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC=.
14.解:∵在直角△ABD中,tan∠BAD==,
∴BD=AD tan∠BAD=12×=9,
∴CD=BC﹣BD=14﹣9=5,
∴AC===13,
∴sinC==.
15.解:(1)∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∠ACB=90°
∴∠BCD+∠ACH=90°
∴∠B=∠BCD=∠CAH,即∠B=∠CAH,
∵AH=2CH,
∴由勾股定理得AC=CH,
∴CH:AC=1:,
∴sinB=;
(2)∵sinB=,
∴AC:AB=1:,
∴AC=2.
∵∠CAH=∠B,
∴sin∠CAH=sinB==,
设CE=x(x>0),则AE=x,则x2+22=(x)2,
∴CE=x=1,AC=2,
在Rt△ABC中,AC2+BC2=AB2,
∵AB=2CD=2,
∴BC=4,
∴BE=BC﹣CE=3.
16.解:(1)在△ABC中,∵∠ACB=90°,
∴sinA==,
而BC=8,
∴AB=10,
∵D是AB中点,
∴CD=AB=5;
(2)在Rt△ABC中,∵AB=10,BC=8,
∴AC==6,
∵D是AB中点,
∴BD=5,S△BDC=S△ADC,
∴S△BDC=S△ABC,即CD BE= AC BC,
∴BE==,
在Rt△BDE中,cos∠DBE===,
即cos∠ABE的值为.
17.解:(1)①如图,作AE⊥PB于点E,
∵△APE中,∠APE=45°,PA=,
∴AE=PE=×=1,
∵PB=4,∴BE=PB﹣PE=3,
在Rt△ABE中,∠AEB=90°,
∴AB==.
②解法一:如图,因为四边形ABCD为正方形,可将
△PAD绕点A顺时针旋转90°得到△P'AB,
可得△PAD≌△P'AB,PD=P'B,PA=P'A.
∴∠PAP'=90°,∠APP'=45°,∠P'PB=90°
∴PP′=PA=2,
∴PD=P′B===;
解法二:如图,过点P作AB的平行线,与DA的延长线交于F,与DA的
延长线交PB于G.
在Rt△AEG中,
可得AG===,EG=,PG=PE﹣EG=.
在Rt△PFG中,
可得PF=PG cos∠FPG=PG cos∠ABE=,FG=.
在Rt△PDF中,可得,
PD===.
(2)如图所示,
将△PAD绕点A顺时针旋转90°
得到△P'AB,PD的最大值即为P'B的最大值,
∵△P'PB中,P'B<PP'+PB,PP′=PA=2,PB=4,
且P、D两点落在直线AB的两侧,
∴当P'、P、B三点共线时,P'B取得最大值(如图)
此时P'B=PP'+PB=6,即P'B的最大值为6.
此时∠APB=180°﹣∠APP'=135度.
18.解:(1)∵AD=2CD,AC=3,
∴AD=2,
∵在Rt△ABC中,∠ACB=90°,AC=BC=3,
∴∠A=∠B=45°,AB===3,
∵DE⊥AB,
∴∠AED=90°,∠ADE=∠A=45°,
∴AE=AD cos45°=2×=,
∴BE=AB﹣AE=3﹣=2,
即线段BE的长为2;
(2)过点E作EH⊥BC,垂足为点H,如图所示:
∵在Rt△BEH中,∠EHB=90°,∠B=45°,
∴EH=BH=BE cos45°=2×=2,
∵BC=3,
∴CH=1,
在Rt△CHE中,cot∠ECB==,
即∠ECB的余切值为.
19.解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,
∴DC=AD=1.
在△ADB中,∵∠ADB=90°,sinB=,AD=1,
∴AB==3,
∴BD==2,
∴BC=BD+DC=2+1;
(2)∵AE是BC边上的中线,
∴CE=BC=+,
∴DE=CE﹣CD=﹣,
∴tan∠DAE==﹣.
20.(1)证明:如图1,连接AD.
∵AB=AC,BD=CD,
∴AD⊥BC.
又∵∠ABC=45°,
∴BD=AB cos∠ABC即AB=BD.
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM.
∴,
∴AE=MD.
(2)解:∵cos60°=,
∴MD=AE cos∠ABC=AE ,即AE=2MD.
∴AE=2MD;
(3)解:如图2,连接AD,EP.
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形.
又∵D为BC的中点,
∴AD⊥BC,∠DAC=30°,BD=DC=AB.
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM.
∴,
∠AEB=∠DMB.
∴EB=2BM.
又∵BM=MP,
∴EB=BP.
∵∠EBM=∠ABC=60°,
∴△BEP为等边三角形,
∴EM⊥BP,
∴∠BMD=90°,
∴∠AEB=90°.
在Rt△AEB中,AE=2,AB=7,
∴BE=.
∴tan∠EAB=.
∵D为BC中点,M为BP中点,
∴DM∥PC.
∴∠MDB=∠PCB,
∴∠EAB=∠PCB.
∴tan∠PCB=.
在Rt△ABD中,AD=AB sin∠ABD=,
在Rt△NDC中,ND=DC tan∠NCD=,
∴NA=AD﹣ND=.
过N作NH⊥AC,垂足为H.
在Rt△ANH中,NH=AN=,AH=AN cos∠NAH=,
∴CH=AC﹣AH=,
∴tan∠ACP=.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
