2021-2022学年北师大版九年级数学下册3.1圆 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.1圆 同步达标测评(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 174.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3.1圆》同步达标测评(附答案)
一.选择题(共9小题,满分36分)
1.AB=12cm,过A、B两点画半径为6cm的圆,能画的圆的个数为( )
A.0个 B.1个 C.2个 D.无数个
2.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
3.下列4个说法中:①直径是弦;②弦是直径;③任何一条直径所在的直线都是圆的对称轴;④弧是半圆;正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=25°,则∠BOC度数是( )
A.40° B.50° C.55° D.60°
5.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形 B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴 D.圆的对称中心是它的圆心
6.如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )
A.40° B.50° C.80° D.100°
7.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B D.无法确定
8.如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为40°、70°、150°,则∠B的度数为( )
A.20° B.25° C.30° D.35°
9.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
二.填空题(共7小题,满分35分)
10.如图,A,B,C是⊙O上三点,∠A=80°,∠C=60°,则∠B的大小为 .
11.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
12.如图,圆O的周长为4π,B是弦CD上任意一点(与C,D不重合),过B作OC的平行线交OD于点E,则EO+EB= .(用数字表示)
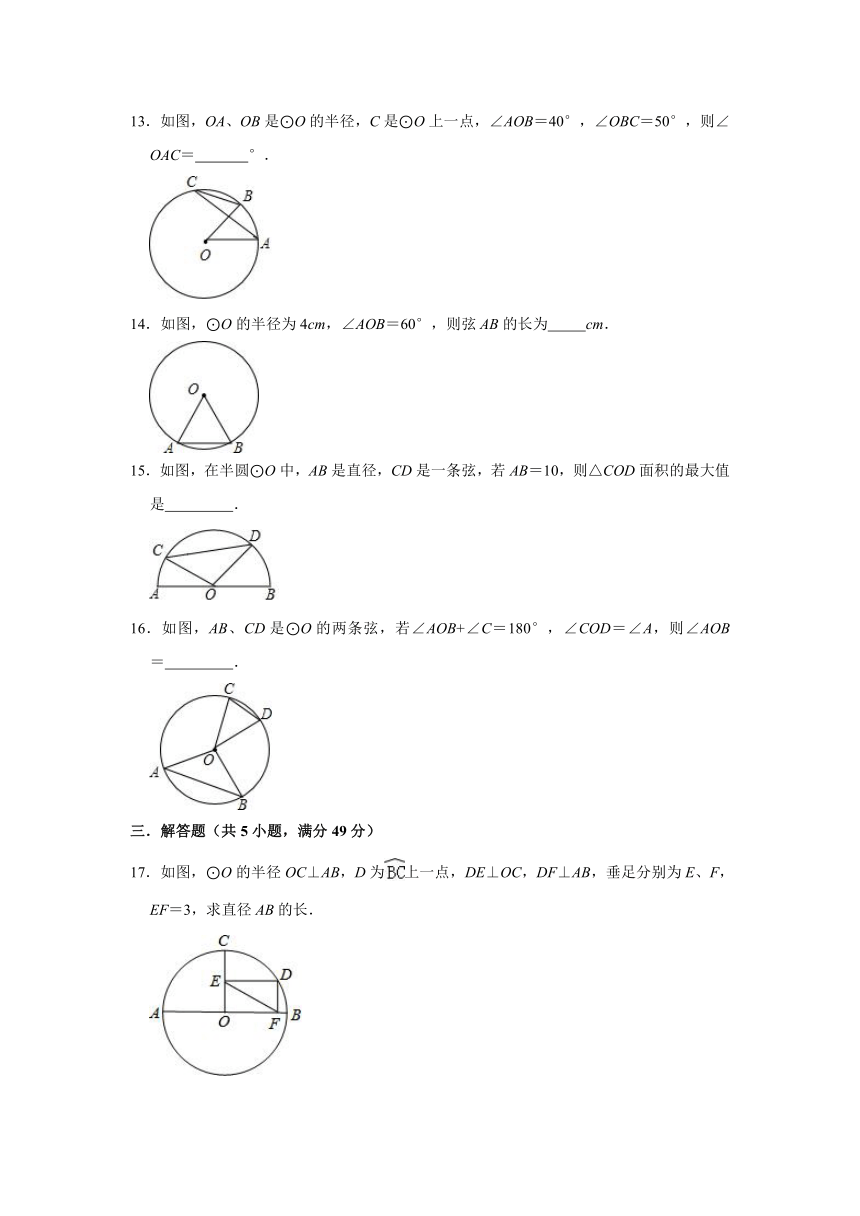
13.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.
14.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 cm.
15.如图,在半圆⊙O中,AB是直径,CD是一条弦,若AB=10,则△COD面积的最大值是 .
16.如图,AB、CD是⊙O的两条弦,若∠AOB+∠C=180°,∠COD=∠A,则∠AOB= .
三.解答题(共5小题,满分49分)
17.如图,⊙O的半径OC⊥AB,D为上一点,DE⊥OC,DF⊥AB,垂足分别为E、F,EF=3,求直径AB的长.
18.如图,BD=OD,∠B=38°,求∠AOD的度数.
19.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.已知AB=2DE,∠AEC=25°,求∠AOC的度数.
20.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
21.已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
参考答案
一.选择题(共9小题,满分36分)
1.解:这样的圆能画1个.如图:
作AB的垂直平分线l,交AB于O点,然后以O为圆心,以6cm为半径作圆,
则⊙O为所求;
故选:B.
2.解:∵圆的半径为6,
∴直径为12,
∵AB是一条弦,
∴AB的长应该小于等于12,不可能为的14,
故选:D.
3.解:①直径是最长的弦,故本小题说法正确;
②弦是不一定是直径,故本小题说法错误;
③经过圆心的每一条直线都是圆的对称轴,故本小题说法正确;
④半圆是弧,但弧不一定是半圆,故本小题说法错误.
故选:B.
4.解:∵OA=OC,
∴∠A=∠ACO=25°,
∴∠BOC=∠A+∠ACO=25°+25°=50°.
故选:B.
5.解:A.圆既是轴对称图形又是中心对称图形,正确;
B.圆的每一条直径所在直线都是它的对称轴,故B错误;
C.圆有无数条对称轴,正确;
D.圆的对称中心是它的圆心,正确.
故选:B.
6.解:∵OM=ON,
∴∠M=∠N=50°,
∴∠MON=180°﹣2×50°=80°.
故选:C.
7.解:π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,
因此两个同时到B点.
故选:C.
8.解:连接OD,如图,
∵∠EOC=40°,∠EOD=70°,∠EOA=150°,
∴∠COD=70°﹣40°=30°,∠DOA=150°﹣70°=80°,
∵OA=OD,
∴∠ODA=∠A=(180°﹣80°)=50°,
∵∠ODA=∠B+∠DOB,
∴∠B=50°﹣30°=20°.
故选:A.
9.解:如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,BD=OC=OA=10,
∴OB===6,
∴AB=OA﹣OB=4,
故选:C.
二.填空题(共7小题,满分35分)
10.解:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA=80°,
∵OB=OC,
∴∠OBC=∠C=60°,
∴∠ABC=∠OBA+∠OBC=80°+60°=140°.
故答案为140°.
11.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
12.解:∵⊙O的周长为4π,
∴OD=2,
∵OC=OD,
∴∠C=∠D,
∵BE∥OC,
∴∠EBD=∠C,
∴∠EBD=∠D,
∴BE=DE,
∴EO+EB=OD=2,
故答案为:2.
13.解:连接OC,
∵OC=OB,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°﹣50°×2=80°,
∴∠AOC=80°+40°=120°,
∵OC=OA,
∴∠OAC=∠OCA=30°,
故答案为:30.
14.解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
15.解:如图,作DH⊥CO交CO的延长线于H.
∵S△COD= OC DH,
∵DH≤OD,
∴当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形,∠COD=90°,
此时面积的最大值为:×5×5=12.5,
故答案为:12.5.
16.解:设∠COD=∠A=x°,
∴∠AOB=(180﹣2x)°,
∠OCD=∠ODC=°,
∵∠AOB+∠C=180°,
∴+180﹣2x=180
解得:x=36
∴∠AOB=(180﹣2x)°=108°,
故答案为:108°.
三.解答题(共5小题,满分49分)
17.解:∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴OD=EF=3,
∴AB=6.
18.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
19.解:连接OD,
∵AB=2DE=2OD,
∴OD=DE,
又∵∠E=25°,
∴∠DOE=∠E=25°,
∴∠ODC=50°,
同理∠C=∠ODC=50°
∴∠AOC=∠E+∠OCE=75°.
20.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
21.证明:∵OA=OB,
∴∠A=∠B,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴∠AOC=∠DOB.
一.选择题(共9小题,满分36分)
1.AB=12cm,过A、B两点画半径为6cm的圆,能画的圆的个数为( )
A.0个 B.1个 C.2个 D.无数个
2.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
3.下列4个说法中:①直径是弦;②弦是直径;③任何一条直径所在的直线都是圆的对称轴;④弧是半圆;正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=25°,则∠BOC度数是( )
A.40° B.50° C.55° D.60°
5.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形 B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴 D.圆的对称中心是它的圆心
6.如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )
A.40° B.50° C.80° D.100°
7.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B D.无法确定
8.如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为40°、70°、150°,则∠B的度数为( )
A.20° B.25° C.30° D.35°
9.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
二.填空题(共7小题,满分35分)
10.如图,A,B,C是⊙O上三点,∠A=80°,∠C=60°,则∠B的大小为 .
11.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
12.如图,圆O的周长为4π,B是弦CD上任意一点(与C,D不重合),过B作OC的平行线交OD于点E,则EO+EB= .(用数字表示)
13.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.
14.如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为 cm.
15.如图,在半圆⊙O中,AB是直径,CD是一条弦,若AB=10,则△COD面积的最大值是 .
16.如图,AB、CD是⊙O的两条弦,若∠AOB+∠C=180°,∠COD=∠A,则∠AOB= .
三.解答题(共5小题,满分49分)
17.如图,⊙O的半径OC⊥AB,D为上一点,DE⊥OC,DF⊥AB,垂足分别为E、F,EF=3,求直径AB的长.
18.如图,BD=OD,∠B=38°,求∠AOD的度数.
19.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.已知AB=2DE,∠AEC=25°,求∠AOC的度数.
20.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
21.已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
参考答案
一.选择题(共9小题,满分36分)
1.解:这样的圆能画1个.如图:
作AB的垂直平分线l,交AB于O点,然后以O为圆心,以6cm为半径作圆,
则⊙O为所求;
故选:B.
2.解:∵圆的半径为6,
∴直径为12,
∵AB是一条弦,
∴AB的长应该小于等于12,不可能为的14,
故选:D.
3.解:①直径是最长的弦,故本小题说法正确;
②弦是不一定是直径,故本小题说法错误;
③经过圆心的每一条直线都是圆的对称轴,故本小题说法正确;
④半圆是弧,但弧不一定是半圆,故本小题说法错误.
故选:B.
4.解:∵OA=OC,
∴∠A=∠ACO=25°,
∴∠BOC=∠A+∠ACO=25°+25°=50°.
故选:B.
5.解:A.圆既是轴对称图形又是中心对称图形,正确;
B.圆的每一条直径所在直线都是它的对称轴,故B错误;
C.圆有无数条对称轴,正确;
D.圆的对称中心是它的圆心,正确.
故选:B.
6.解:∵OM=ON,
∴∠M=∠N=50°,
∴∠MON=180°﹣2×50°=80°.
故选:C.
7.解:π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,
因此两个同时到B点.
故选:C.
8.解:连接OD,如图,
∵∠EOC=40°,∠EOD=70°,∠EOA=150°,
∴∠COD=70°﹣40°=30°,∠DOA=150°﹣70°=80°,
∵OA=OD,
∴∠ODA=∠A=(180°﹣80°)=50°,
∵∠ODA=∠B+∠DOB,
∴∠B=50°﹣30°=20°.
故选:A.
9.解:如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,BD=OC=OA=10,
∴OB===6,
∴AB=OA﹣OB=4,
故选:C.
二.填空题(共7小题,满分35分)
10.解:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA=80°,
∵OB=OC,
∴∠OBC=∠C=60°,
∴∠ABC=∠OBA+∠OBC=80°+60°=140°.
故答案为140°.
11.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
12.解:∵⊙O的周长为4π,
∴OD=2,
∵OC=OD,
∴∠C=∠D,
∵BE∥OC,
∴∠EBD=∠C,
∴∠EBD=∠D,
∴BE=DE,
∴EO+EB=OD=2,
故答案为:2.
13.解:连接OC,
∵OC=OB,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°﹣50°×2=80°,
∴∠AOC=80°+40°=120°,
∵OC=OA,
∴∠OAC=∠OCA=30°,
故答案为:30.
14.解:∵OA=OB,
而∠AOB=60°,
∴△OAB为等边三角形,
∴AB=OA=4cm.
故答案为4.
15.解:如图,作DH⊥CO交CO的延长线于H.
∵S△COD= OC DH,
∵DH≤OD,
∴当DH=OD时,△COD的面积最大,此时△COD是等腰直角三角形,∠COD=90°,
此时面积的最大值为:×5×5=12.5,
故答案为:12.5.
16.解:设∠COD=∠A=x°,
∴∠AOB=(180﹣2x)°,
∠OCD=∠ODC=°,
∵∠AOB+∠C=180°,
∴+180﹣2x=180
解得:x=36
∴∠AOB=(180﹣2x)°=108°,
故答案为:108°.
三.解答题(共5小题,满分49分)
17.解:∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴OD=EF=3,
∴AB=6.
18.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
19.解:连接OD,
∵AB=2DE=2OD,
∴OD=DE,
又∵∠E=25°,
∴∠DOE=∠E=25°,
∴∠ODC=50°,
同理∠C=∠ODC=50°
∴∠AOC=∠E+∠OCE=75°.
20.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
21.证明:∵OA=OB,
∴∠A=∠B,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴∠AOC=∠DOB.
