2021-2022学年北师大版九年级数学下册3.2圆的对称性 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性 同步达标测评(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 557.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:38:17 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.2圆的对称性》同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠OFE的度数是( )
A.30° B.20° C.40° D.35°
2.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A. B.3 C.3 D.4
3.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连接AB、AD,若AD=,则半径R的长为( )
A.1 B. C. D.
4.如图,AB为半圆⊙O的直径,AB=10,AC为⊙O的弦,AC=8,D为的中点,DM⊥AC于M,则DM的长为( )
A. B. C.1 D.
5.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于120°,那么圆心O到弦AB的距离等于( )
A.1 B. C.2 D.
6.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10 B.13 C.15 D.16
7.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
8.下列说法正确的是( )
A.等弧所对的弦相等 B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等 D.相等的圆心角所对的弧相等
9.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④+=+,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
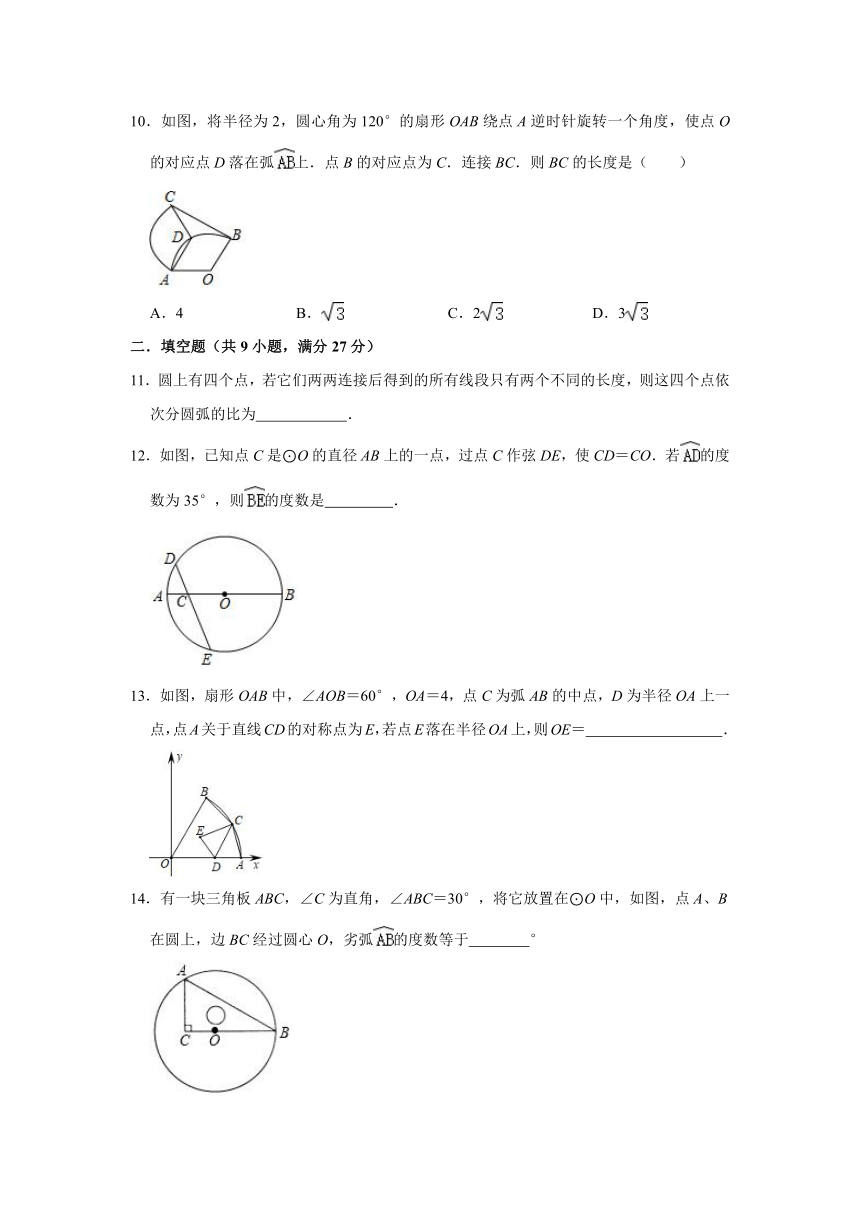
10.如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转一个角度,使点O的对应点D落在弧上.点B的对应点为C.连接BC.则BC的长度是( )
A.4 B. C.2 D.3
二.填空题(共9小题,满分27分)
11.圆上有四个点,若它们两两连接后得到的所有线段只有两个不同的长度,则这四个点依次分圆弧的比为 .
12.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
13.如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE= .
14.有一块三角板ABC,∠C为直角,∠ABC=30°,将它放置在⊙O中,如图,点A、B在圆上,边BC经过圆心O,劣弧的度数等于 °
15.如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°圆弧多次复制并首尾连接而成,现有一点P从A(A为坐标原点),以每秒米的速度沿曲线向右运动,则在第2020秒时点P的纵坐标为 .
16.如图,在△ABC中,∠BAC=52°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是 .
17.如图,AB是⊙O的直径,M、N分别是AO,BO的中点,CM⊥AB,DN⊥AB,则的度数 .
18.如图1,一艺术拱门由两部分组成,下部为矩形ABCD,AB,AD的长分别是2m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为 m.
19.如图,已知四边形ABCD外接圆⊙O的半径为5,对角线AC与BD交于点E,BE=DE,AB=BE,且AC=8,则四边形ABCD的面积为 .
三.解答题(共8小题,满分63分)
20.如图,四边形ABCD中,AB∥CD,点O在BD上,以O为圆心恰好经过A、B、C三点,⊙O交BD于E,交AD于F,且=,连接OA、OF.
(1)求证:四边形ABCD是菱形;
(2)若∠AOF=3∠FOE,求∠ABC的度数.
21.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
22.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
23.如图,AB、AC是⊙O的两条弦,M是的中点,N是的中点,弦MN分别交AB、AC于点P、D.
(1)求证:AP=AD;
(2)连接PO,当AP=3,OP=,⊙O的半径为5,求MP的长.
24.如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.
25.如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
26.如图,AB是O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证:CF=BF;
(2)若AD=6,⊙O的半径为5,求BC的长.
27.已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且=.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
参考答案
一.选择题(共10小题,满分30分)
1.解:如图,连接BF,OE.
∵EF=EB,OE=OE,OF=OB,
∴△OEF≌△OEB(SSS),
∴∠OFE=∠OBE,
∵OE=OB=OF,
∴∠OEF=∠OFE=∠OEB=∠OBE,∠OFB=∠OBF,
∵∠ABF=∠AOF=20°,
∴∠OFB=∠OBE=20°,
∵∠OFB+∠OBF+∠OFE+∠OBE+∠BEF=180°,
∴4∠EFO+40°=180°,
∴∠OFE=35°,
解法二:∵∠AOF=40°,
∴∠BOF=140°,
∴∠FEB=∠BOF=70°,
∵EF=EB,
∴∠EFB=∠EBF=55°,
∵OF=OB,
∴∠OFB=∠OBF=20°,
∴∠EFO=∠EFB﹣∠OFB=55°﹣20°=25°.
故选:D.
2.解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
3.解:∵弦AC=BD,
∴,
∴,
∴∠ABD=∠BAC,
∴AE=BE;
如图,连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=,
∴R=1,
故选:A.
4.解:如图,连接OD交AC于H,连接BC.
∵AB是直径,
∴∠ACB=90°,
∴BC==6,
∵=,
∴OD⊥AB,
∵∠OAH=∠CAB,∠AOH=∠ACB=90°,
∴△AOH∽△ACB,
∴==
∴==
∴OH=,AH=,
∵DH=OD﹣OH=5﹣=,
∵DM⊥AC,
∵∠DMH=∠AOH=90°,∠DHM=∠AHO,
∴△DMH∽△AOH,
∴=,
∴=,
∴DM=1,
故选:C.
5.解:如图,∵圆心角∠AOB=120°,OA=OB,
∴△OAB是等腰三角形,
∵OC⊥AB,
∴∠ACO=90°,∠A=30°,
∴OC=OA=2.
故选:C.
6.解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,=,
∵点D是弧AC的中点,
∴=,
∴=,
∴AC=DF=12,
∴EF=DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x﹣3)2,
解得x=,
∴AB=2x=15,
故选:C.
7.解:∵根据圆周角定理得:∠AOC=2∠ABC,
∵∠ABC+∠AOC=75°,
∴∠AOC=×75°=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:C.
8.解:A、正确.本选项符合题意.
B、错误.应该是平分弦(此弦非直径)的直径垂直弦并平分弦所对的弧,本选项不符合题意.
C、错误,必须在同圆或等圆中,本选项不符合题意.
D、错误.必须在同圆或等圆中,本选项不符合题意.
故选:A.
9.解:∵F为的中点,
∴=,故①正确,
∴∠FCM=∠FAC,
∵∠ACF=∠ACM+∠MCF,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴=,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴的度数+的度数=180°,
∴的度数+的度数=180°,
∴+=+=+=+,故④正确,
故选:C.
10.解:如图,连接OD,BD.
由题意:OA=OD=AD,
∴△AOD是等边三角形,
∴∠ADO=∠AOD=60°,
∵∠ADC=∠AOB=120°,
∴∠ADO+∠ADC=180°,
∴O,D,C共线,
∵∠AOD=∠DOB=60°,OD=OB,
∴△OBD是等边三角形,
∴∠BDO=60°,
∵DC=DB,
∴∠DCB=∠DBC=30°,
∴∠OBC=90°,
∴BC=OB=2,
故选:C.
二.填空题(共9小题,满分27分)
11.解:∵四个点两两连接后得到的所有线段只有两个不同的长度,
∴圆上的四个点构成了圆的内接正方形,
∵正方形的边长相等,即四条弦长相等,
∴这四个点依次分圆弧的比为1:1:1:1.
故答案为1:1:1:1.
12.解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=110°,
∴∠AOE=75°,
∴∠BOE=105°,
∴的度数是105°.
故答案为105°.
13.解:连接OC,作EF⊥OC于F,
∵点A关于直线CD的对称点为E,点E落在半径OA上,
∴CE=CA,
∵=,
∴∠AOC=∠AOB=30°,
∵OA=OC,
∴∠OAC=∠OCA=75°,
∵CE=CA,
∴∠CAE=∠CEA=75°,
∴∠CAE=30°,
∴∠ECF=45°,
设EF=x,则FC=x,
在Rt△EOF中,tan∠EOF=,
∴OF==x,
由题意得,OF+FC=OC,即x+x=4,
解得,x=2﹣2,
∵∠EOF=30°,
∴OE=2EF=4﹣4,
故答案为:4﹣4.
14.解:如图,连接OA.
.∵OA=OB,
∴∠OAB=∠B=30°,
∴∠AOB=120°,
∴弧AC的度数为120°.
故答案为120.
15.解:点运动一个用时为÷π=2秒.
如图,作CD⊥AB于D,交于点E.
在Rt△ACD中,∵∠ADC=90°,∠ACD=∠ACB=60°,
∴∠CAD=30°,
∴CD=AC=×2=1,
∴DE=CE﹣CD=2﹣1=1,
∴第1秒时点P运动到点E,纵坐标为1;
第2秒时点P运动到点B,纵坐标为0;
第3秒时点P运动到点F,纵坐标为﹣1;
第4秒时点P运动到点G,纵坐标为0;
第5秒时点P运动到点H,纵坐标为1;
…,
∴点P的纵坐标以1,0,﹣1,0四个数为一个周期依次循环,
∵2020÷4=505,
∴第2020秒时点P的纵坐标为是0.
故答案为0.
16.解:∵△ABC中∠BAC=52°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣52°)=64°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣64°=116°.
故答案是:116°.
17.解:∵AB是⊙O的直径,M、N分别是AO,BO的中点,
∴2OM=OC,2ON=OD,
∵CM⊥AB,DN⊥AB,
∴∠CMO=∠DNO=90°,
∴∠MCO=∠NDO=30°,
∴∠MOC=∠NOD=60°,
∴∠COD=180°﹣60°﹣60°=60°,
∴的度数是60°,
故答案为:60°
18.解:如图所示,过点O作垂直于地面的直线与拱门外框上沿交于点P,交地面于点Q,
如图1,AB,AD的长分别是2m和4m,圆心角∠COD=120°,
∴∠DOP=60°,DC=AB=m,
∴OD=2m,PQ=5m,
当点P在线段AD上时,拱门上的点到地面的最大距离h等于点D到地面的距离,即点P与点D重合时,此时
h===m,
如图2所示,当点P在劣弧CD上时,拱门上的点到地面的最大距离h等于⊙O的半径长与圆心O到地面的距离之和,
易知,OQ≤OB,
而h=OP+OQ=2+OQ,
∴当点Q与点B重合时,h取得最大值,
由图1可知,OQ=3m,BQ=m,则OB=m,
h的最大值为OP+OB,即(2+)m.
故答案为:(2+).
19.解:∵BE=DE,AB=BE,
∴AB2=2BE2=BE BD,
∴AB:BE=BD:AB,
又∠EBA=∠ABD,
∴△ABE∽△DBA,
∴∠ADB=∠BAE,
∵∠ADB=∠ACB,
∴∠ACB=∠CAB,
∴AB=BC.
连接BO,交AC于H,连接OA,
∵AB=BC,
∴BO⊥AC,
∴CH=AH,
∴CH=AH=AC=4
∵AO=5,
∴OH==3,BH=OB﹣OH=5﹣3=2.
∴S△ABC=AC BH=×8×2=8,
∵E是BD的中点,
∴S△ABE=S△ADE,S△BCE=S△DCE,
∴S△ABC=S△ADC,
∴S四边形ABCD=2S△ABC=16,
故答案为16.
三.解答题(共8小题,满分63分)
20.(1)证明:∵=,
∴∠CBD=∠ABD,
∵CD∥AB,
∴∠ABD=∠CDB,
∴∠CBD=∠CDB,
∴CB=CD,
∵BE是⊙O的直径,
∴=,
∴AB=BC=CD,
∵CD∥AB,
∴四边形ABCD是菱形;.
(2)∵∠AOF=3∠FOE,
设∠FOE=x,则∠AOF=3x,
∠AOD=∠FOE+∠AOF=4x,
∵OA=OF,
∴∠OAF=∠OFA=(180°﹣3x),
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD,
∴∠ABC+∠BAD=180°,
∴4x+2x+(180°﹣3x)=180°,
解得:x=20°,
∴∠ABC=4x=80°.
21.(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
22.解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∴∠DCO=90°,
∵∠POM=45°,
∴∠CDO=45°,
∴CD=CO,
∴BO=BC+CO=BC+CD,
∴BO=2AB,
连接AO,如图:
∵MN=10,
∴AO=5,
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,
解得:AB=,
则正方形ABCD的边长为.
23.(1)证明:连AM,AN,
∵=,=,
∴∠BAM=∠ANM,∠AMN=∠CAN,
∵∠APD=∠AMN+∠BAM,∠ADP=∠CAN+∠ANM,
∴∠APD=∠ADP,
∴AP=AD.
(2 )解:连AO,OM交AB于E,设PE=x,
∵=,
∴OM⊥AB,
∴∠AEO=90°,
∵OE2=OA2﹣AE2=OP2﹣PE2
∴52﹣(x+3)2=()2﹣x2,
∴x=1,
∴AE=4,OE=3,ME=2,
∴MP===.
24.(1)证明:∵AB=CD,
∴=,
∵M是的中点,
∴=,
∴=,
∴BM=DM.
(2)解:如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2,
∵OE=1,∠OEM=90°,
∴OM===,
∴⊙O的半径为.
25.证明:连OC,AC,如图,
∵∠AOB=120°,C是弧AB的中点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∴AC=AO,
∵OA⊥CE,
∴=,
∴AE=AC,
∴AE=AO.
26.(1)证明:连接AC,如图1所示:
∵C是弧BD的中点,
∴∠DBC=∠BAC,
在ABC中,∠ACB=90°,CE⊥AB,
∴∠BCE+∠ECA=∠BAC+∠ECA=90°,
∴∠BCE=∠BAC,
又C是弧BD的中点,
∴∠DBC=∠CDB,
∴∠BCE=∠DBC,
∴CF=BF.
(2)解:连接OC交BD于G,如图2所示:
∵AB是O的直径,AB=2OC=10,
∴∠ADB=90°,
∴BD===8,
∵C是弧BD的中点,
∴OC⊥BD,DG=BG=BD=4,
∵OA=OB,
∴OG是△ABD的中位线,
∴OG=AD=3,
∴CG=OC﹣OG=5﹣3=2,
在Rt△BCG中,由勾股定理得:BC===2.
27.解:(1)连接DF、DG.
∵BD是⊙O的直径,
∴∠DFB=∠DGB=90°,
∵=,
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A,
∠DGB=∠HDG+∠C,
∴∠A=∠C.
(2)结论:α+β+θ=180°.
理由:如图②中,连接DF,BH.
∵=,
∴∠ADF=∠HBG=θ,
∵∠AFD+∠DFB=180°,∠DFB+∠DHB=180°,
∴∠AFD=∠DHB,
∵∠A+∠ADF+∠AFD=180°,∠AFD=∠DHB=∠C+∠HBG,
∴∠A+θ+∠C+θ=180°,
∴α+β+θ=180°
一.选择题(共10小题,满分30分)
1.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠OFE的度数是( )
A.30° B.20° C.40° D.35°
2.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A. B.3 C.3 D.4
3.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连接AB、AD,若AD=,则半径R的长为( )
A.1 B. C. D.
4.如图,AB为半圆⊙O的直径,AB=10,AC为⊙O的弦,AC=8,D为的中点,DM⊥AC于M,则DM的长为( )
A. B. C.1 D.
5.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于120°,那么圆心O到弦AB的距离等于( )
A.1 B. C.2 D.
6.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10 B.13 C.15 D.16
7.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25° B.50° C.65° D.75°
8.下列说法正确的是( )
A.等弧所对的弦相等 B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等 D.相等的圆心角所对的弧相等
9.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④+=+,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转一个角度,使点O的对应点D落在弧上.点B的对应点为C.连接BC.则BC的长度是( )
A.4 B. C.2 D.3
二.填空题(共9小题,满分27分)
11.圆上有四个点,若它们两两连接后得到的所有线段只有两个不同的长度,则这四个点依次分圆弧的比为 .
12.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
13.如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE= .
14.有一块三角板ABC,∠C为直角,∠ABC=30°,将它放置在⊙O中,如图,点A、B在圆上,边BC经过圆心O,劣弧的度数等于 °
15.如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为120°圆弧多次复制并首尾连接而成,现有一点P从A(A为坐标原点),以每秒米的速度沿曲线向右运动,则在第2020秒时点P的纵坐标为 .
16.如图,在△ABC中,∠BAC=52°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是 .
17.如图,AB是⊙O的直径,M、N分别是AO,BO的中点,CM⊥AB,DN⊥AB,则的度数 .
18.如图1,一艺术拱门由两部分组成,下部为矩形ABCD,AB,AD的长分别是2m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为 m.
19.如图,已知四边形ABCD外接圆⊙O的半径为5,对角线AC与BD交于点E,BE=DE,AB=BE,且AC=8,则四边形ABCD的面积为 .
三.解答题(共8小题,满分63分)
20.如图,四边形ABCD中,AB∥CD,点O在BD上,以O为圆心恰好经过A、B、C三点,⊙O交BD于E,交AD于F,且=,连接OA、OF.
(1)求证:四边形ABCD是菱形;
(2)若∠AOF=3∠FOE,求∠ABC的度数.
21.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
22.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
23.如图,AB、AC是⊙O的两条弦,M是的中点,N是的中点,弦MN分别交AB、AC于点P、D.
(1)求证:AP=AD;
(2)连接PO,当AP=3,OP=,⊙O的半径为5,求MP的长.
24.如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.
25.如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
26.如图,AB是O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证:CF=BF;
(2)若AD=6,⊙O的半径为5,求BC的长.
27.已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且=.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
参考答案
一.选择题(共10小题,满分30分)
1.解:如图,连接BF,OE.
∵EF=EB,OE=OE,OF=OB,
∴△OEF≌△OEB(SSS),
∴∠OFE=∠OBE,
∵OE=OB=OF,
∴∠OEF=∠OFE=∠OEB=∠OBE,∠OFB=∠OBF,
∵∠ABF=∠AOF=20°,
∴∠OFB=∠OBE=20°,
∵∠OFB+∠OBF+∠OFE+∠OBE+∠BEF=180°,
∴4∠EFO+40°=180°,
∴∠OFE=35°,
解法二:∵∠AOF=40°,
∴∠BOF=140°,
∴∠FEB=∠BOF=70°,
∵EF=EB,
∴∠EFB=∠EBF=55°,
∵OF=OB,
∴∠OFB=∠OBF=20°,
∴∠EFO=∠EFB﹣∠OFB=55°﹣20°=25°.
故选:D.
2.解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
3.解:∵弦AC=BD,
∴,
∴,
∴∠ABD=∠BAC,
∴AE=BE;
如图,连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=R,
∵AD=,
∴R=1,
故选:A.
4.解:如图,连接OD交AC于H,连接BC.
∵AB是直径,
∴∠ACB=90°,
∴BC==6,
∵=,
∴OD⊥AB,
∵∠OAH=∠CAB,∠AOH=∠ACB=90°,
∴△AOH∽△ACB,
∴==
∴==
∴OH=,AH=,
∵DH=OD﹣OH=5﹣=,
∵DM⊥AC,
∵∠DMH=∠AOH=90°,∠DHM=∠AHO,
∴△DMH∽△AOH,
∴=,
∴=,
∴DM=1,
故选:C.
5.解:如图,∵圆心角∠AOB=120°,OA=OB,
∴△OAB是等腰三角形,
∵OC⊥AB,
∴∠ACO=90°,∠A=30°,
∴OC=OA=2.
故选:C.
6.解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,=,
∵点D是弧AC的中点,
∴=,
∴=,
∴AC=DF=12,
∴EF=DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x﹣3)2,
解得x=,
∴AB=2x=15,
故选:C.
7.解:∵根据圆周角定理得:∠AOC=2∠ABC,
∵∠ABC+∠AOC=75°,
∴∠AOC=×75°=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:C.
8.解:A、正确.本选项符合题意.
B、错误.应该是平分弦(此弦非直径)的直径垂直弦并平分弦所对的弧,本选项不符合题意.
C、错误,必须在同圆或等圆中,本选项不符合题意.
D、错误.必须在同圆或等圆中,本选项不符合题意.
故选:A.
9.解:∵F为的中点,
∴=,故①正确,
∴∠FCM=∠FAC,
∵∠ACF=∠ACM+∠MCF,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴=,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴的度数+的度数=180°,
∴的度数+的度数=180°,
∴+=+=+=+,故④正确,
故选:C.
10.解:如图,连接OD,BD.
由题意:OA=OD=AD,
∴△AOD是等边三角形,
∴∠ADO=∠AOD=60°,
∵∠ADC=∠AOB=120°,
∴∠ADO+∠ADC=180°,
∴O,D,C共线,
∵∠AOD=∠DOB=60°,OD=OB,
∴△OBD是等边三角形,
∴∠BDO=60°,
∵DC=DB,
∴∠DCB=∠DBC=30°,
∴∠OBC=90°,
∴BC=OB=2,
故选:C.
二.填空题(共9小题,满分27分)
11.解:∵四个点两两连接后得到的所有线段只有两个不同的长度,
∴圆上的四个点构成了圆的内接正方形,
∵正方形的边长相等,即四条弦长相等,
∴这四个点依次分圆弧的比为1:1:1:1.
故答案为1:1:1:1.
12.解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=110°,
∴∠AOE=75°,
∴∠BOE=105°,
∴的度数是105°.
故答案为105°.
13.解:连接OC,作EF⊥OC于F,
∵点A关于直线CD的对称点为E,点E落在半径OA上,
∴CE=CA,
∵=,
∴∠AOC=∠AOB=30°,
∵OA=OC,
∴∠OAC=∠OCA=75°,
∵CE=CA,
∴∠CAE=∠CEA=75°,
∴∠CAE=30°,
∴∠ECF=45°,
设EF=x,则FC=x,
在Rt△EOF中,tan∠EOF=,
∴OF==x,
由题意得,OF+FC=OC,即x+x=4,
解得,x=2﹣2,
∵∠EOF=30°,
∴OE=2EF=4﹣4,
故答案为:4﹣4.
14.解:如图,连接OA.
.∵OA=OB,
∴∠OAB=∠B=30°,
∴∠AOB=120°,
∴弧AC的度数为120°.
故答案为120.
15.解:点运动一个用时为÷π=2秒.
如图,作CD⊥AB于D,交于点E.
在Rt△ACD中,∵∠ADC=90°,∠ACD=∠ACB=60°,
∴∠CAD=30°,
∴CD=AC=×2=1,
∴DE=CE﹣CD=2﹣1=1,
∴第1秒时点P运动到点E,纵坐标为1;
第2秒时点P运动到点B,纵坐标为0;
第3秒时点P运动到点F,纵坐标为﹣1;
第4秒时点P运动到点G,纵坐标为0;
第5秒时点P运动到点H,纵坐标为1;
…,
∴点P的纵坐标以1,0,﹣1,0四个数为一个周期依次循环,
∵2020÷4=505,
∴第2020秒时点P的纵坐标为是0.
故答案为0.
16.解:∵△ABC中∠BAC=52°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣52°)=64°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣64°=116°.
故答案是:116°.
17.解:∵AB是⊙O的直径,M、N分别是AO,BO的中点,
∴2OM=OC,2ON=OD,
∵CM⊥AB,DN⊥AB,
∴∠CMO=∠DNO=90°,
∴∠MCO=∠NDO=30°,
∴∠MOC=∠NOD=60°,
∴∠COD=180°﹣60°﹣60°=60°,
∴的度数是60°,
故答案为:60°
18.解:如图所示,过点O作垂直于地面的直线与拱门外框上沿交于点P,交地面于点Q,
如图1,AB,AD的长分别是2m和4m,圆心角∠COD=120°,
∴∠DOP=60°,DC=AB=m,
∴OD=2m,PQ=5m,
当点P在线段AD上时,拱门上的点到地面的最大距离h等于点D到地面的距离,即点P与点D重合时,此时
h===m,
如图2所示,当点P在劣弧CD上时,拱门上的点到地面的最大距离h等于⊙O的半径长与圆心O到地面的距离之和,
易知,OQ≤OB,
而h=OP+OQ=2+OQ,
∴当点Q与点B重合时,h取得最大值,
由图1可知,OQ=3m,BQ=m,则OB=m,
h的最大值为OP+OB,即(2+)m.
故答案为:(2+).
19.解:∵BE=DE,AB=BE,
∴AB2=2BE2=BE BD,
∴AB:BE=BD:AB,
又∠EBA=∠ABD,
∴△ABE∽△DBA,
∴∠ADB=∠BAE,
∵∠ADB=∠ACB,
∴∠ACB=∠CAB,
∴AB=BC.
连接BO,交AC于H,连接OA,
∵AB=BC,
∴BO⊥AC,
∴CH=AH,
∴CH=AH=AC=4
∵AO=5,
∴OH==3,BH=OB﹣OH=5﹣3=2.
∴S△ABC=AC BH=×8×2=8,
∵E是BD的中点,
∴S△ABE=S△ADE,S△BCE=S△DCE,
∴S△ABC=S△ADC,
∴S四边形ABCD=2S△ABC=16,
故答案为16.
三.解答题(共8小题,满分63分)
20.(1)证明:∵=,
∴∠CBD=∠ABD,
∵CD∥AB,
∴∠ABD=∠CDB,
∴∠CBD=∠CDB,
∴CB=CD,
∵BE是⊙O的直径,
∴=,
∴AB=BC=CD,
∵CD∥AB,
∴四边形ABCD是菱形;.
(2)∵∠AOF=3∠FOE,
设∠FOE=x,则∠AOF=3x,
∠AOD=∠FOE+∠AOF=4x,
∵OA=OF,
∴∠OAF=∠OFA=(180°﹣3x),
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD,
∴∠ABC+∠BAD=180°,
∴4x+2x+(180°﹣3x)=180°,
解得:x=20°,
∴∠ABC=4x=80°.
21.(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
22.解:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∴∠DCO=90°,
∵∠POM=45°,
∴∠CDO=45°,
∴CD=CO,
∴BO=BC+CO=BC+CD,
∴BO=2AB,
连接AO,如图:
∵MN=10,
∴AO=5,
在Rt△ABO中,AB2+BO2=AO2,
即AB2+(2AB)2=52,
解得:AB=,
则正方形ABCD的边长为.
23.(1)证明:连AM,AN,
∵=,=,
∴∠BAM=∠ANM,∠AMN=∠CAN,
∵∠APD=∠AMN+∠BAM,∠ADP=∠CAN+∠ANM,
∴∠APD=∠ADP,
∴AP=AD.
(2 )解:连AO,OM交AB于E,设PE=x,
∵=,
∴OM⊥AB,
∴∠AEO=90°,
∵OE2=OA2﹣AE2=OP2﹣PE2
∴52﹣(x+3)2=()2﹣x2,
∴x=1,
∴AE=4,OE=3,ME=2,
∴MP===.
24.(1)证明:∵AB=CD,
∴=,
∵M是的中点,
∴=,
∴=,
∴BM=DM.
(2)解:如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2,
∵OE=1,∠OEM=90°,
∴OM===,
∴⊙O的半径为.
25.证明:连OC,AC,如图,
∵∠AOB=120°,C是弧AB的中点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∴AC=AO,
∵OA⊥CE,
∴=,
∴AE=AC,
∴AE=AO.
26.(1)证明:连接AC,如图1所示:
∵C是弧BD的中点,
∴∠DBC=∠BAC,
在ABC中,∠ACB=90°,CE⊥AB,
∴∠BCE+∠ECA=∠BAC+∠ECA=90°,
∴∠BCE=∠BAC,
又C是弧BD的中点,
∴∠DBC=∠CDB,
∴∠BCE=∠DBC,
∴CF=BF.
(2)解:连接OC交BD于G,如图2所示:
∵AB是O的直径,AB=2OC=10,
∴∠ADB=90°,
∴BD===8,
∵C是弧BD的中点,
∴OC⊥BD,DG=BG=BD=4,
∵OA=OB,
∴OG是△ABD的中位线,
∴OG=AD=3,
∴CG=OC﹣OG=5﹣3=2,
在Rt△BCG中,由勾股定理得:BC===2.
27.解:(1)连接DF、DG.
∵BD是⊙O的直径,
∴∠DFB=∠DGB=90°,
∵=,
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A,
∠DGB=∠HDG+∠C,
∴∠A=∠C.
(2)结论:α+β+θ=180°.
理由:如图②中,连接DF,BH.
∵=,
∴∠ADF=∠HBG=θ,
∵∠AFD+∠DFB=180°,∠DFB+∠DHB=180°,
∴∠AFD=∠DHB,
∵∠A+∠ADF+∠AFD=180°,∠AFD=∠DHB=∠C+∠HBG,
∴∠A+θ+∠C+θ=180°,
∴α+β+θ=180°
