2021-2022学年北师大版九年级数学下册3.3垂径定理 同步达标测评 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.3垂径定理 同步达标测评 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 396.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:39:05 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3.3垂径定理》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
1.在平面直角坐标系中,若以A(2,﹣1)为圆心,2为半径的⊙A与过点B(1,0)的直线交于C、D,则CD的最小值为( )
A. B.2 C.2 D.4
2.如图,⊙O中弦AB长为8,OC⊥AB,垂足为E,若CE=2,则⊙O半径长是( )
A.10 B.8 C.6 D.5
3.已知水平放置的圆柱形排水管道,管道截面半径是1m,若水面高0.2m.则排水管道截面的水面宽度为( )
A.0.6m B.0.8m C.1.2m D.1.6m
4.如图,某圆弧形拱桥的跨度AB=12米,拱高CD=4米,则该拱桥的半径为( )
A.15米 B.13米 C.9米 D.6.5米
5.如图,在⊙O中,半径OC⊥AB于点D,AD=4,则下列说法正确的是( )
A.OC=4 B.AB=8
C.OD=3 D.AB垂直平分OC
6.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=20,CD=16,则BE的长为( )
A.2 B.4 C.5 D.6
7.如图,⊙O的半径为5,弦AB长为8,P为弦AB上动点,则线段OP长的取值范围是( )
A.3<OP<5 B.3≤OP≤5 C.4<OP<5 D.4≤OP≤5
8.在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,当油面宽变为8分米,油面AB上升( )
A.1分米 B.4分米
C.3分米 D.1分米或7分米
9.抛一个铁球,在泥地上砸了一个直径8cm,深2cm的坑,这个铁球的直径是( )
A.12cm B.10cm C.8cm D.6cm
10.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
二.填空题(共7小题,满分28分)
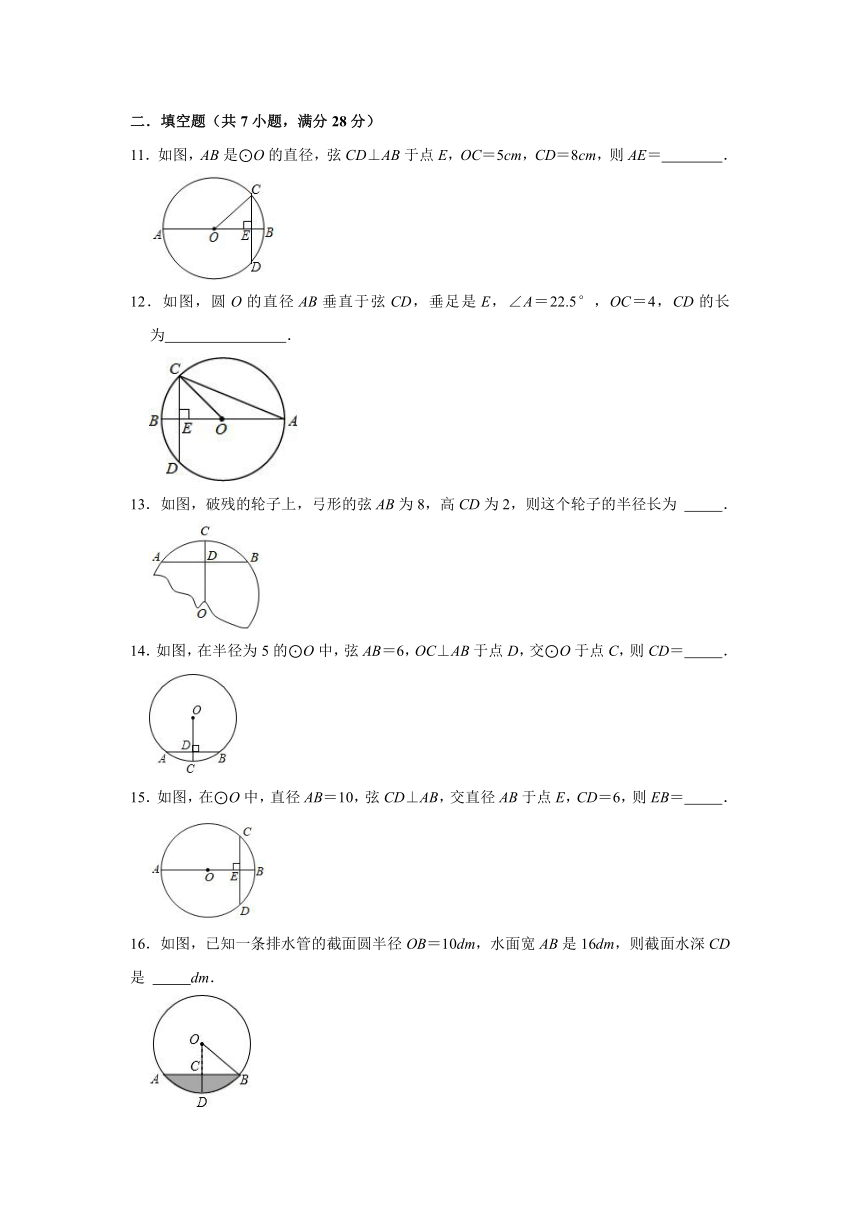
11.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE= .
12.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 .
13.如图,破残的轮子上,弓形的弦AB为8,高CD为2,则这个轮子的半径长为 .
14.如图,在半径为5的⊙O中,弦AB=6,OC⊥AB于点D,交⊙O于点C,则CD= .
15.如图,在⊙O中,直径AB=10,弦CD⊥AB,交直径AB于点E,CD=6,则EB= .
16.如图,已知一条排水管的截面圆半径OB=10dm,水面宽AB是16dm,则截面水深CD是 dm.
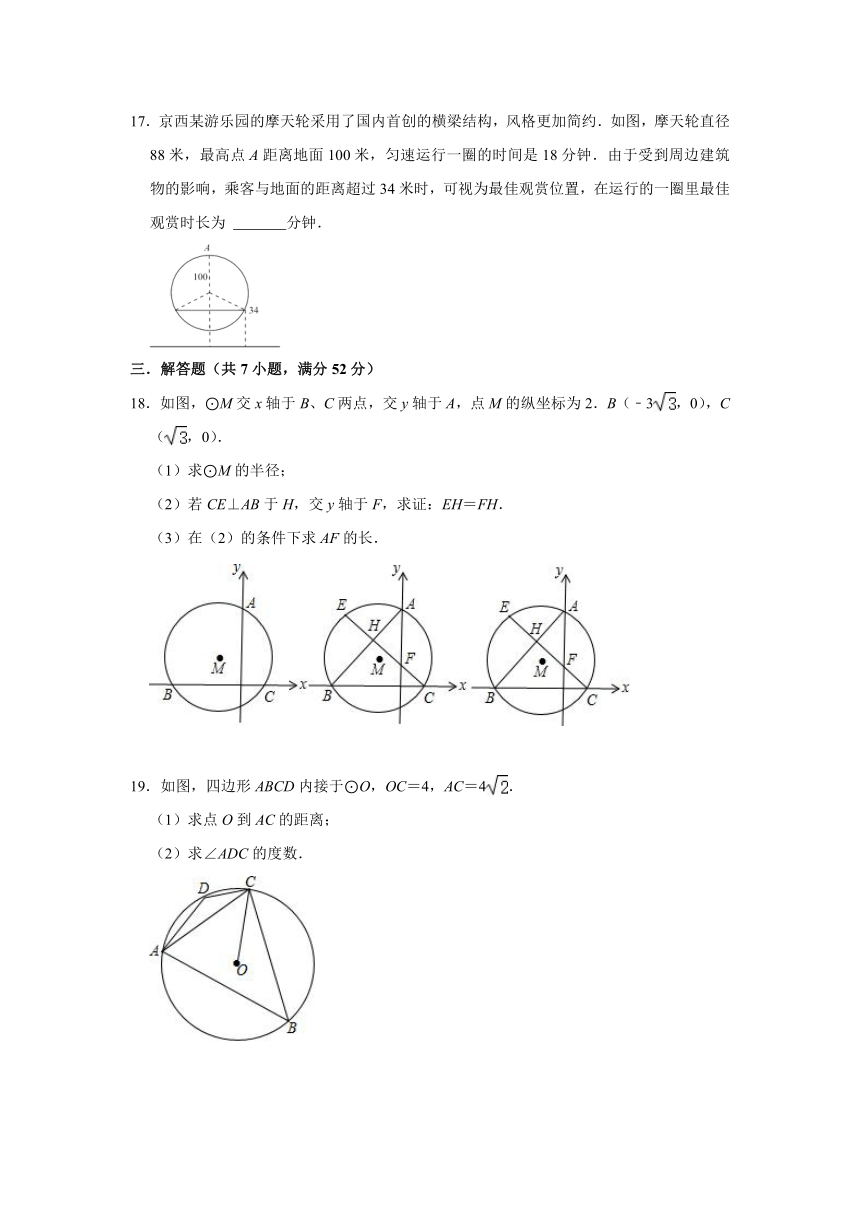
17.京西某游乐园的摩天轮采用了国内首创的横梁结构,风格更加简约.如图,摩天轮直径88米,最高点A距离地面100米,匀速运行一圈的时间是18分钟.由于受到周边建筑物的影响,乘客与地面的距离超过34米时,可视为最佳观赏位置,在运行的一圈里最佳观赏时长为 分钟.
三.解答题(共7小题,满分52分)
18.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3,0),C(,0).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.
19.如图,四边形ABCD内接于⊙O,OC=4,AC=4.
(1)求点O到AC的距离;
(2)求∠ADC的度数.
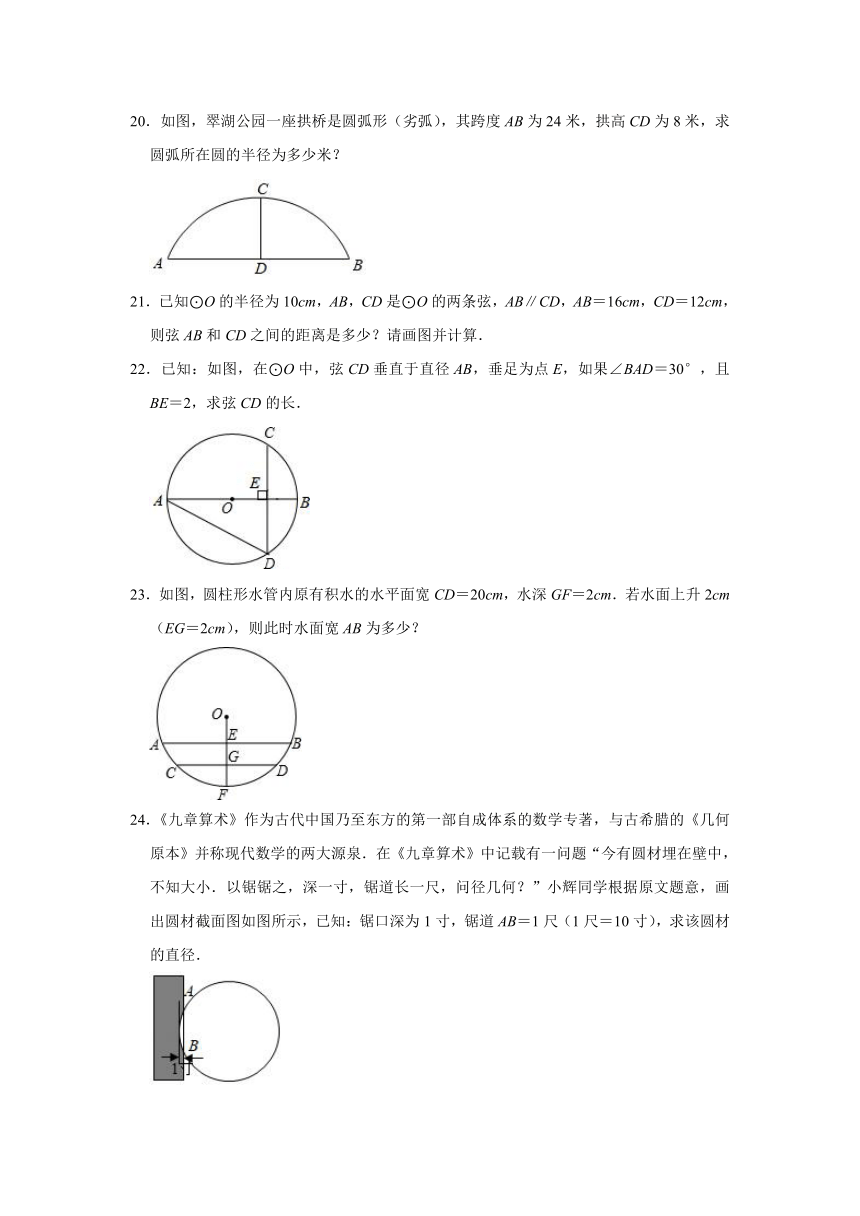
20.如图,翠湖公园一座拱桥是圆弧形(劣弧),其跨度AB为24米,拱高CD为8米,求圆弧所在圆的半径为多少米?
21.已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是多少?请画图并计算.
22.已知:如图,在⊙O中,弦CD垂直于直径AB,垂足为点E,如果∠BAD=30°,且BE=2,求弦CD的长.
23.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
24.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),求该圆材的直径.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,连接AC,作AE⊥CD于E,
∴CE=DE=CD,CE=
∵AC=2,
∴当AE取最大值时,CE最小,即CD最小,
∴当E点与B重合时,AE最大,
∵A(2,﹣1),B(1,0),
∴AB2=(2﹣1)2+(﹣1﹣0)2=2,
∴CE的最小值为:==,
∴CD的最小值为2,
故选:C.
2.解:连接OA,
设⊙O的半径为r,则OC=OA=r,OE=OC﹣CE=r﹣2,
∵OC⊥AB,AB=8,
∴AE=BE=AB=4,
在Rt△OAE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径长为5,
故选:D.
3.解:作OC⊥AB于C,交⊙O于D,连接OB,如图所示:
则AB=2BC,∠OCB=90°,OB=OD=1m,CD=0.2m,
∴OC=OD﹣CD=0.8m,
∴BC===0.6(m),
∴AB=2AC=1.2m,
∴排水管道截面的水面宽度为1.2m,
故选:C.
4.解:根据垂径定理的推论知,圆弧形拱桥的圆心在CD所在的直线上,
设圆心是O,半径是r米,连接OA.
根据垂径定理,得:AD=AB=6(米),
在Rt△AOD中,根据勾股定理,得r2=62+(r﹣4)2,
解得:r=6.5,
即该拱桥的半径为6.5米,
故选:D.
5.解:∵半径OC⊥AB于点D,AD=4,
∴AB=2AD=8,OC>AD=4,
∵半径没有确定,
∴OD=3不正确,
当OD=CD时,AB垂直平分OC,
∴选项B符合题意,选项A、C、D不符合题意,
故选:B.
6.解:∵AB是⊙O的直径,弦CD⊥AB于点E,AB=20,
∴CO=OB=10,AB⊥CD,CE=DE=CD,
∵CD=16,
∴CE=8,
在Rt△COE中,OE=,
∴BE=OB﹣OE=10﹣6=4,
故选:B.
7.解:过点O作OH⊥AB于H,连接OB,
则AH=HB=AB=4,
在Rt△OBH中,OH===3,
∴线段OP长的取值范围是3≤OP≤5,
故选:B.
8.解:连接OA.作OG⊥AB于G,
则在直角△OAG中,AG=3分米,
因为OA=5cm,根据勾股定理得到:OG=4分米,即弦AB的弦心距是4分米,
同理当油面宽AB为8分米时,弦心距是3分米,
当油面没超过圆心O时,油上升了1分米;当油面超过圆心O时,油上升了7分米.
因而油上升了1分米或7分米.
故选:D.
9.解:设该铅球的半径是rcm.
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,
根据勾股定理,得r2=(r﹣2)2+16,
解得r=5,
故2r=10.
故选:B.
10.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
二.填空题(共7小题,满分28分)
11.解:∵弦CD⊥AB于点E,CD=8cm,
∴CE=CD=4(cm)
在Rt△OCE中,OC=5cm,CE=4cm,
∴OE===3(cm),
∴AE=AO+OE=5+3=8(cm).
故答案为:8cm.
12.解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
故答案为4.
13.解:连接OB,如图所示:
由题意得:OC⊥AB,
∴AD=BD=AB=4,
在Rt△OBD中,根据勾股定理得:OD2+BD2=OB2,
即(OB﹣1)2+42=OB2,
解得:OB=5,
即这个轮子的半径长为5,
故答案为:5.
14.解:连接OA,
∵AB=6,OC⊥AB于点D,
∴AD=AB=×6=3,
∵⊙O的半径为5,
∴OD===4,
∴CD=OC﹣OD=5﹣4=1.
故答案为:1.
15.解:连接OC,如图所示:
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3,
在Rt△OEC中,∠OEC=90°,CE=3,OC=AB=5,
∴OE==4,
∴BE=OB﹣OE=AB﹣OE=5﹣4=1,
故答案为:1.
16.解:由题意知OD⊥AB,交AB于点C,
∵AB=16dm,
∴BC=AB=8(dm),
在Rt△OBC中,OB=10dm,BC=8dm,
∴OC===6(dm),
∴CD=OD﹣OC=10﹣6=4(dm).
故答案为:4.
17.解:如图所示:
摩天轮转动的角速度为:360°÷18分=20°/分,
由题意得:AD⊥BC,AD=88米,AM=100米,CM=BN=34米,
则OB=OD=44(米),DM=AM﹣AD=12(米),
∴CD=CM﹣DM=34﹣12=22(米),
∴OC=OD﹣CD=22(米),
∴OC=OB,
∵∠OCB=90°,
∴∠OBC=30°,
∴∠BOC=90°﹣30°=60°,
∴∠AOB=180°﹣∠BOC=120°,
∴最佳观赏位置的圆心角为2×120°=240°,
∴在运行的一圈里最佳观赏时长为:240°÷20°/分=12(分钟),
故答案为:12.
三.解答题(共7小题,满分52分)
18.解:(1)如图(一),过M作MT⊥BC于T连BM,
∵BC是⊙M的一条弦,MT是垂直于BC的直径,
∴BT=TC=BC=2,
∴BM==4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH.
在△AEH和△AFH中,
∵,
∴△AEH≌△AFH(AAS),
∴EH=FH.
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
∵⊙O的半径为4,
∴CG=4.
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.
19.解:(1)作OM⊥AC于M,
∵AC=4,
∴AM=CM=2,
∵OC=4,
∴OM==2;
(2)连接OA,
∵OM=MC,∠OMC=90°,
∴∠MOC=∠MCO=45°,
∵OA=OC,
∴∠OAM=45°,
∴∠AOC=90°,
∴∠B=45°,
∵∠D+∠B=180°,
∴∠D=135°.
20.解:延长CD到O,使得OC=OA,如图所示:
则O为圆心,
∵CD为拱高,
∴OC⊥AB,
∴AD=AB=12(米),
设圆弧所在圆O的半径为x米,
则OD=(x﹣8)米,
在Rt△AOD中,由勾股定理得:AD2+OD2=OA2,
即122+(x﹣8)2=x2,
解得:x=13,
答:圆弧所在圆的半径为13米.
21.解:有两种情况:①圆心O在弦AB和CD的同旁,如图,连接OC、OA,
过O作OE⊥AB于E,且直线OE交CD于F,
∵AB∥CD,
∴OF⊥CD,
∴∠OFC=90°,∠OEA=90°,
∵OE⊥AB,OE过O,AB=16cm,
∴AE=BE=8cm,
推理CF=DF=6cm,
由勾股定理得:OE===6(cm),
OF===8(cm),
∴EF=OF﹣OE=2cm;
②圆心O在弦AB和弦CD之间,如图,
此时EF=OE+OF=14cm,
所以弦AB和CD之间的距离是2cm或14cm.
22.解:连接OD,设⊙O的半径为r,则OE=r﹣2,
∵∠BAD=30°,
∴∠DOE=60°,
∵CD⊥AB,
∴CD=2DE,∠ODE=30°,
∴OD=2OE,即r=2(r﹣2),解得r=4;
∴OE=4﹣2=2,
∴DE===2,
∴CD=2DE=4.
23.解:连接OA、OC,
∵由题意知:AB∥CD,OE⊥AB,OF⊥CD,CD=20cm,
∴CG=CD=10cm,
在Rt△OGC中,由勾股定理得:OC2=CG2+OG2,
OC2=102+(OC﹣2)2,
解得:OC=26(cm),
则OE=26cm﹣2cm﹣2cm=22cm,
∵在Rt△OEA中,由勾股定理得:OA2=OE2+AE2,
∴262=222+AE2,
∴AE=8,
∵OE⊥AB,OE过圆心O,
∴AB=2AE=16cm.
24.解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA,如图所示:
∴AC=AB=×10=5,
设⊙O的半径为r寸,
在Rt△ACO中,OC=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸.
一.选择题(共10小题,满分40分)
1.在平面直角坐标系中,若以A(2,﹣1)为圆心,2为半径的⊙A与过点B(1,0)的直线交于C、D,则CD的最小值为( )
A. B.2 C.2 D.4
2.如图,⊙O中弦AB长为8,OC⊥AB,垂足为E,若CE=2,则⊙O半径长是( )
A.10 B.8 C.6 D.5
3.已知水平放置的圆柱形排水管道,管道截面半径是1m,若水面高0.2m.则排水管道截面的水面宽度为( )
A.0.6m B.0.8m C.1.2m D.1.6m
4.如图,某圆弧形拱桥的跨度AB=12米,拱高CD=4米,则该拱桥的半径为( )
A.15米 B.13米 C.9米 D.6.5米
5.如图,在⊙O中,半径OC⊥AB于点D,AD=4,则下列说法正确的是( )
A.OC=4 B.AB=8
C.OD=3 D.AB垂直平分OC
6.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=20,CD=16,则BE的长为( )
A.2 B.4 C.5 D.6
7.如图,⊙O的半径为5,弦AB长为8,P为弦AB上动点,则线段OP长的取值范围是( )
A.3<OP<5 B.3≤OP≤5 C.4<OP<5 D.4≤OP≤5
8.在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,当油面宽变为8分米,油面AB上升( )
A.1分米 B.4分米
C.3分米 D.1分米或7分米
9.抛一个铁球,在泥地上砸了一个直径8cm,深2cm的坑,这个铁球的直径是( )
A.12cm B.10cm C.8cm D.6cm
10.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
二.填空题(共7小题,满分28分)
11.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE= .
12.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 .
13.如图,破残的轮子上,弓形的弦AB为8,高CD为2,则这个轮子的半径长为 .
14.如图,在半径为5的⊙O中,弦AB=6,OC⊥AB于点D,交⊙O于点C,则CD= .
15.如图,在⊙O中,直径AB=10,弦CD⊥AB,交直径AB于点E,CD=6,则EB= .
16.如图,已知一条排水管的截面圆半径OB=10dm,水面宽AB是16dm,则截面水深CD是 dm.
17.京西某游乐园的摩天轮采用了国内首创的横梁结构,风格更加简约.如图,摩天轮直径88米,最高点A距离地面100米,匀速运行一圈的时间是18分钟.由于受到周边建筑物的影响,乘客与地面的距离超过34米时,可视为最佳观赏位置,在运行的一圈里最佳观赏时长为 分钟.
三.解答题(共7小题,满分52分)
18.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3,0),C(,0).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.
19.如图,四边形ABCD内接于⊙O,OC=4,AC=4.
(1)求点O到AC的距离;
(2)求∠ADC的度数.
20.如图,翠湖公园一座拱桥是圆弧形(劣弧),其跨度AB为24米,拱高CD为8米,求圆弧所在圆的半径为多少米?
21.已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是多少?请画图并计算.
22.已知:如图,在⊙O中,弦CD垂直于直径AB,垂足为点E,如果∠BAD=30°,且BE=2,求弦CD的长.
23.如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽AB为多少?
24.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),求该圆材的直径.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,连接AC,作AE⊥CD于E,
∴CE=DE=CD,CE=
∵AC=2,
∴当AE取最大值时,CE最小,即CD最小,
∴当E点与B重合时,AE最大,
∵A(2,﹣1),B(1,0),
∴AB2=(2﹣1)2+(﹣1﹣0)2=2,
∴CE的最小值为:==,
∴CD的最小值为2,
故选:C.
2.解:连接OA,
设⊙O的半径为r,则OC=OA=r,OE=OC﹣CE=r﹣2,
∵OC⊥AB,AB=8,
∴AE=BE=AB=4,
在Rt△OAE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径长为5,
故选:D.
3.解:作OC⊥AB于C,交⊙O于D,连接OB,如图所示:
则AB=2BC,∠OCB=90°,OB=OD=1m,CD=0.2m,
∴OC=OD﹣CD=0.8m,
∴BC===0.6(m),
∴AB=2AC=1.2m,
∴排水管道截面的水面宽度为1.2m,
故选:C.
4.解:根据垂径定理的推论知,圆弧形拱桥的圆心在CD所在的直线上,
设圆心是O,半径是r米,连接OA.
根据垂径定理,得:AD=AB=6(米),
在Rt△AOD中,根据勾股定理,得r2=62+(r﹣4)2,
解得:r=6.5,
即该拱桥的半径为6.5米,
故选:D.
5.解:∵半径OC⊥AB于点D,AD=4,
∴AB=2AD=8,OC>AD=4,
∵半径没有确定,
∴OD=3不正确,
当OD=CD时,AB垂直平分OC,
∴选项B符合题意,选项A、C、D不符合题意,
故选:B.
6.解:∵AB是⊙O的直径,弦CD⊥AB于点E,AB=20,
∴CO=OB=10,AB⊥CD,CE=DE=CD,
∵CD=16,
∴CE=8,
在Rt△COE中,OE=,
∴BE=OB﹣OE=10﹣6=4,
故选:B.
7.解:过点O作OH⊥AB于H,连接OB,
则AH=HB=AB=4,
在Rt△OBH中,OH===3,
∴线段OP长的取值范围是3≤OP≤5,
故选:B.
8.解:连接OA.作OG⊥AB于G,
则在直角△OAG中,AG=3分米,
因为OA=5cm,根据勾股定理得到:OG=4分米,即弦AB的弦心距是4分米,
同理当油面宽AB为8分米时,弦心距是3分米,
当油面没超过圆心O时,油上升了1分米;当油面超过圆心O时,油上升了7分米.
因而油上升了1分米或7分米.
故选:D.
9.解:设该铅球的半径是rcm.
在由铅球的半径、小坑的半径即半弦和弦心距组成的直角三角形中,
根据勾股定理,得r2=(r﹣2)2+16,
解得r=5,
故2r=10.
故选:B.
10.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
二.填空题(共7小题,满分28分)
11.解:∵弦CD⊥AB于点E,CD=8cm,
∴CE=CD=4(cm)
在Rt△OCE中,OC=5cm,CE=4cm,
∴OE===3(cm),
∴AE=AO+OE=5+3=8(cm).
故答案为:8cm.
12.解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
故答案为4.
13.解:连接OB,如图所示:
由题意得:OC⊥AB,
∴AD=BD=AB=4,
在Rt△OBD中,根据勾股定理得:OD2+BD2=OB2,
即(OB﹣1)2+42=OB2,
解得:OB=5,
即这个轮子的半径长为5,
故答案为:5.
14.解:连接OA,
∵AB=6,OC⊥AB于点D,
∴AD=AB=×6=3,
∵⊙O的半径为5,
∴OD===4,
∴CD=OC﹣OD=5﹣4=1.
故答案为:1.
15.解:连接OC,如图所示:
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3,
在Rt△OEC中,∠OEC=90°,CE=3,OC=AB=5,
∴OE==4,
∴BE=OB﹣OE=AB﹣OE=5﹣4=1,
故答案为:1.
16.解:由题意知OD⊥AB,交AB于点C,
∵AB=16dm,
∴BC=AB=8(dm),
在Rt△OBC中,OB=10dm,BC=8dm,
∴OC===6(dm),
∴CD=OD﹣OC=10﹣6=4(dm).
故答案为:4.
17.解:如图所示:
摩天轮转动的角速度为:360°÷18分=20°/分,
由题意得:AD⊥BC,AD=88米,AM=100米,CM=BN=34米,
则OB=OD=44(米),DM=AM﹣AD=12(米),
∴CD=CM﹣DM=34﹣12=22(米),
∴OC=OD﹣CD=22(米),
∴OC=OB,
∵∠OCB=90°,
∴∠OBC=30°,
∴∠BOC=90°﹣30°=60°,
∴∠AOB=180°﹣∠BOC=120°,
∴最佳观赏位置的圆心角为2×120°=240°,
∴在运行的一圈里最佳观赏时长为:240°÷20°/分=12(分钟),
故答案为:12.
三.解答题(共7小题,满分52分)
18.解:(1)如图(一),过M作MT⊥BC于T连BM,
∵BC是⊙M的一条弦,MT是垂直于BC的直径,
∴BT=TC=BC=2,
∴BM==4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH.
在△AEH和△AFH中,
∵,
∴△AEH≌△AFH(AAS),
∴EH=FH.
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
∵⊙O的半径为4,
∴CG=4.
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.
19.解:(1)作OM⊥AC于M,
∵AC=4,
∴AM=CM=2,
∵OC=4,
∴OM==2;
(2)连接OA,
∵OM=MC,∠OMC=90°,
∴∠MOC=∠MCO=45°,
∵OA=OC,
∴∠OAM=45°,
∴∠AOC=90°,
∴∠B=45°,
∵∠D+∠B=180°,
∴∠D=135°.
20.解:延长CD到O,使得OC=OA,如图所示:
则O为圆心,
∵CD为拱高,
∴OC⊥AB,
∴AD=AB=12(米),
设圆弧所在圆O的半径为x米,
则OD=(x﹣8)米,
在Rt△AOD中,由勾股定理得:AD2+OD2=OA2,
即122+(x﹣8)2=x2,
解得:x=13,
答:圆弧所在圆的半径为13米.
21.解:有两种情况:①圆心O在弦AB和CD的同旁,如图,连接OC、OA,
过O作OE⊥AB于E,且直线OE交CD于F,
∵AB∥CD,
∴OF⊥CD,
∴∠OFC=90°,∠OEA=90°,
∵OE⊥AB,OE过O,AB=16cm,
∴AE=BE=8cm,
推理CF=DF=6cm,
由勾股定理得:OE===6(cm),
OF===8(cm),
∴EF=OF﹣OE=2cm;
②圆心O在弦AB和弦CD之间,如图,
此时EF=OE+OF=14cm,
所以弦AB和CD之间的距离是2cm或14cm.
22.解:连接OD,设⊙O的半径为r,则OE=r﹣2,
∵∠BAD=30°,
∴∠DOE=60°,
∵CD⊥AB,
∴CD=2DE,∠ODE=30°,
∴OD=2OE,即r=2(r﹣2),解得r=4;
∴OE=4﹣2=2,
∴DE===2,
∴CD=2DE=4.
23.解:连接OA、OC,
∵由题意知:AB∥CD,OE⊥AB,OF⊥CD,CD=20cm,
∴CG=CD=10cm,
在Rt△OGC中,由勾股定理得:OC2=CG2+OG2,
OC2=102+(OC﹣2)2,
解得:OC=26(cm),
则OE=26cm﹣2cm﹣2cm=22cm,
∵在Rt△OEA中,由勾股定理得:OA2=OE2+AE2,
∴262=222+AE2,
∴AE=8,
∵OE⊥AB,OE过圆心O,
∴AB=2AE=16cm.
24.解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA,如图所示:
∴AC=AB=×10=5,
设⊙O的半径为r寸,
在Rt△ACO中,OC=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸.
