2021-2022学年北师大版九年级数学下册3.7切线长定理 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.7切线长定理 同步达标测评(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 279.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:42:06 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.7切线长定理》同步达标测评(附答案)
一.选择题(共8小题,满分32分)
1.以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为( )
A.12 B.13 C.14 D.15
2.如图,直角梯形ABCD中,以AD为直径的半圆与BC相切于E,BO交半圆于F,DF的延长线交AB于点P,连DE.以下结论:①DE∥OF;②AB+CD=BC;③PB=PF;④AD2=4AB DC.其中正确的是( )
A.①②③④ B.只有①② C.只有①②④ D.只有③④
3.P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是( )
A.4 B.8 C.12 D.不能确定
4.已知P为⊙O外一点,PA,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=( )
A.35°、145° B.110°、70° C.55°、125° D.110°
5.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为( )
A.5 B.10 C.7.5 D.4
6.如图,⊙O的外切梯形ABCD中,若AD∥BC,那么∠DOC的度数为( )
A.70° B.90° C.60° D.45°
7.如图所示,已知PA、PB切⊙O于A、B两点,C是上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )
A.56° B.60° C.62° D.不可求
8.如图,在平行四边形ABCD中,AB=15,过点D作一圆与AB、BC分别相切于G、H,与边AD、CD相交于点E、F,且5AE=4DE,8CF=DF,则BH等于( )
A.5 B.6 C.7 D.8
二.填空题(共8小题,满分32分)
9.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,则∠CPD= .
10.一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环,当滚到与坡面BC开始相切时停止.其AB=40cm,BC与水平面的夹角为60°.其圆心所经过的路线长是 cm(结果保留根号).
11.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.
(1)若△PDE的周长为10,则PA的长为 ;
(2)连接CA、CB,若∠P=50°,则∠BCA的度数为 度.
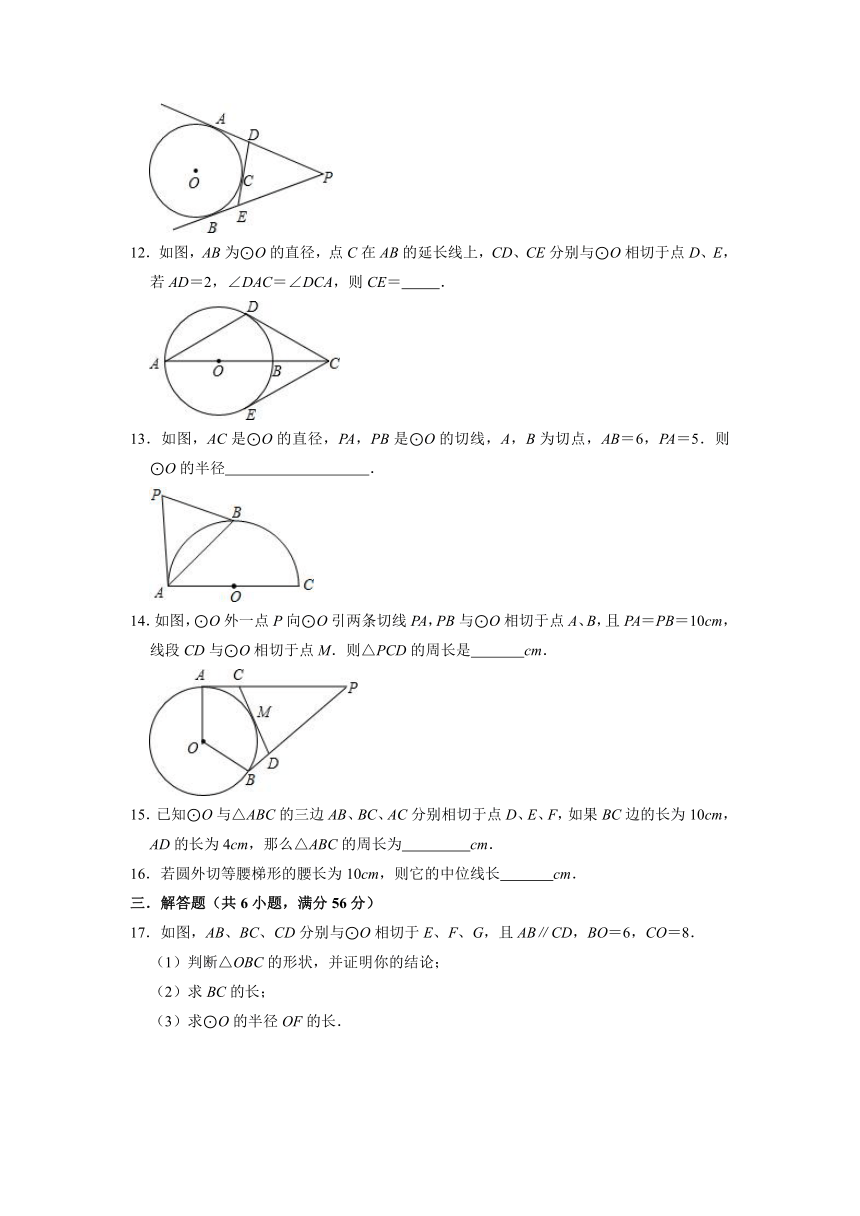
12.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,则CE= .
13.如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,AB=6,PA=5.则⊙O的半径 .
14.如图,⊙O外一点P向⊙O引两条切线PA,PB与⊙O相切于点A、B,且PA=PB=10cm,线段CD与⊙O相切于点M.则△PCD的周长是 cm.
15.已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,如果BC边的长为10cm,AD的长为4cm,那么△ABC的周长为 cm.
16.若圆外切等腰梯形的腰长为10cm,则它的中位线长 cm.
三.解答题(共6小题,满分56分)
17.如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.
(1)判断△OBC的形状,并证明你的结论;
(2)求BC的长;
(3)求⊙O的半径OF的长.
18.如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.
19.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是上的任意一点,过点C的切线分别交PA、PB于点D、E.
(1)若PA=4,求△PED的周长;
(2)若∠P=40°,求∠AFB的度数.
20.已知:如图△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,过D作⊙O的切线交BC于点E,EF⊥AB,垂足为F.
(1)求证:DE=BC;
(2)若AC=6,BC=8,求S△ACD:S△EDF的值.
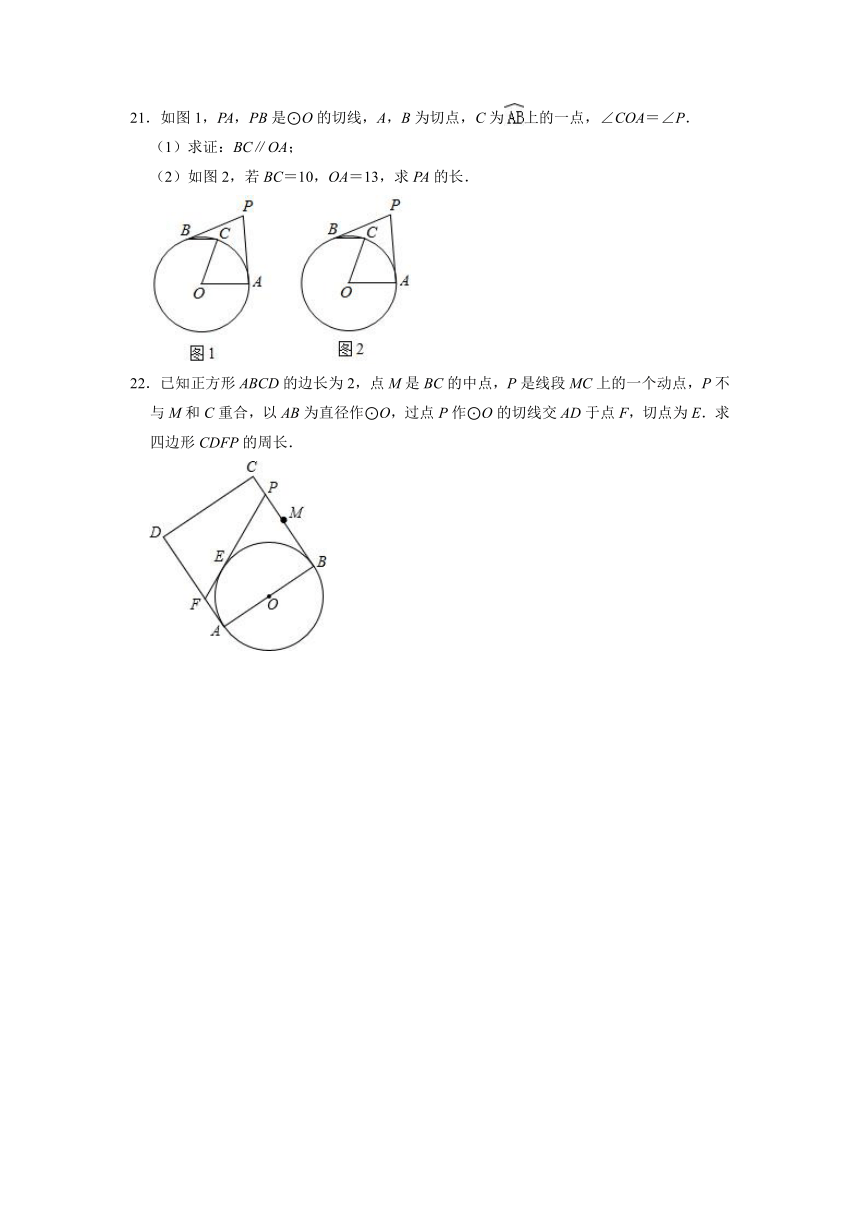
21.如图1,PA,PB是⊙O的切线,A,B为切点,C为上的一点,∠COA=∠P.
(1)求证:BC∥OA;
(2)如图2,若BC=10,OA=13,求PA的长.
22.已知正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点,P不与M和C重合,以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E.求四边形CDFP的周长.
参考答案
一.选择题(共8小题,满分32分)
1.解:设AE的长为x,正方形ABCD的边长为a,
∵CE与半圆O相切于点F,
∴AE=EF,BC=CF,
∵EF+FC+CD+ED=12,
∴AE+ED+CD+BC=12,
∵AD=CD=BC=AB,
∴正方形ABCD的边长为4;
在Rt△CDE中,ED2+CD2=CE2,即(4﹣x)2+42=(4+x)2,解得:x=1,
∵AE+EF+FC+BC+AB=14,
∴直角梯形ABCE周长为14.
故选:C.
2.解:∵BA,BE是圆的切线.
∴AB=BE,BO是△ABE顶角的平分线.
∴OB⊥AE
∵AD是圆的直径.
∴DE⊥AE
∴DE∥OF
故①正确;
∵CD=CE,AB=BE
∴AB+CD=BC
故②正确;
∵OD=OF
∴∠ODF=∠OFD=∠BFP
若PB=PF,则有∠PBF=∠BFP=∠ODF
而△ADP与△ABO不一定相似,故PB=PF不一定成了.
故③不正确;
连接OC.可以证明△OAB∽△CDO
∴
即:OA OD=AB CD
∴AD2=4AB DC
故④正确.
故正确的是:①②④.
故选:C.
3.解:根据题意画出图形,如图所示,
由直线DA和直线DC为圆O的切线,得到AD=DC,同理,由直线EC和直线EB为圆O的切线,得到EC=EB,
又直线PA和直线PB为圆O的切线,所以PA=PB=4,
则△PDE的周长C=PD+DE+PE=PD+DC+EC+PE
=PD+DA+EB+PE=PA+PB=4+4=8.
故选:B.
4.解:如图;连接OA、OB,则∠OAP=∠OBP=90°,
∴∠BOA=180°﹣∠P=110°,
∴∠AEB=∠AOB=55°;
∵四边形AEBF是⊙O的内接四边形,
∴∠AFB=180°﹣∠AEB=125°,
①当C点在优弧AB上运动时,∠BCA=∠AEB=55°;
②当C′点在劣弧AB上运动时,∠BC′A=∠AFB=125°;
故选:C.
5.解:设AF=x,根据切线长定理得AD=x,BD=BE=9﹣x,CE=CF=CA﹣AF=6﹣x,
则有9﹣x+6﹣x=5,解得x=5,即AF的长为5.
故选:A.
6.解:∵DA、CD、CB都与⊙O相切,
∴∠ADO=∠ODC,∠OCD=∠OCB;
∵AD∥BC,
∴∠ADC+∠BCD=180°;
∴∠ODC+∠OCD=(∠ADC+∠BCD)=×180°=90°,即∠DOC=90°;
故选:B.
7.解:∠PMN+∠PNM=180°﹣∠P=124°,
∠AMN+∠BNM=360°﹣124°=236°,
∵MA、MC是⊙O的切线,
∴∠AMO=∠CMO,
∵NB、NC是⊙O的切线,
∴∠BNO=∠CNO,
∴∠CMO+∠CNO=(∠AMN+∠BNM)=118°,
∴∠MON=180°﹣118°=62°,
故选:C.
8.解:由8CF=DF,得CF=15×=,
则CH2=CF×DC,
故CH=5,
设BC=x,则BH=x﹣5=BG,
故AG=20﹣x,
又∵5AE=4DE,
∴DE=x,AE=x,
则AG2=AE×AD,则(20﹣x)2=x2,
解得:x=12,
故BH=BC﹣CH=7.
故选:C.
二.填空题(共8小题,满分32分)
9.解:∵PA=6,⊙O的半径为2,
∴PB=PA﹣AB=6﹣4=2,
∴OP=4,
∵PC、PD切⊙O于点C、D.
∴∠OPC=∠OPD,
∴CO⊥PC,
∴sin∠OPC==,
∴∠OPC=30°,
∴∠CPD=60°,
故答案为:60°.
10.解:连接OD、BD,作DE⊥AB,
∵BC与水平面的夹角为60°,
∴∠DBE=60°,
∴∠BDE=30°,
设BE=x,则BD=2x,
∴由勾股定理得4x2﹣x2=25,
解得x=,
∴OD=AE=40﹣,
故答案为40﹣.
11.解:(1)∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB,DA=DC,EC=EB;
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10;
∴PA=PB=5;
(2)连接OA、OB、AC、BC,在⊙O上取一点F,连接AF、BF,
∵PA、PB分别切⊙O 于A、B;
∴∠PAO=∠PRO=90°
∴∠AOB=360°﹣90°﹣90°﹣50°=130°;
∴∠AFB=∠AOB=65°,
∵∠AFB+∠BCA=180°
∴∠BCA=180°﹣65°=115°;
故答案是:5,115°.
12.解:∵CD、CE分别与⊙O相切于点D、E,
∴CD=CE,
∵∠DAC=∠DCA,
∴AD=CD,
∴AD=CE,
∵AD=2,
∴CE=2.
故答案为:2.
13.解:连接OP,OB,
∵AP为⊙O切线,PB为⊙O切线,
∴PA=PB,
∵∠APO=∠BPO,
PG=PG,
∴△APG≌△BPG,
∴∠PGA=90°,
∵△APO为直角三角形,
∠APG=∠APG,
∴△PGA∽△PAO,
根据垂径定理,得到AG=GB,
在Rt△PAG中,PG==4,
∵△PGA∽△AGO,
∴=,
∴=,
∴AO=.
故答案为:.
14.解:∵CM,CA是圆的切线,
∴CA=CM,
同理,DM=DB,
∴△PCD的周长=PC+PD+CD=PC+CM+DM+PD=PC+CA+PD+BD=PA+PB=20cm.
故答案为:20.
15.解:
∵⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,BC=10cm,AD=4cm,
∴AD=AF=4cm,BE=BD,CF=CE,
即BD+CF=BE+CE=BC=10cm,
∴△ABC的周长是AB+BC+AC=AD+BD+BC+CF+AF=4cm+10cm+10cm+4cm=28cm,
故答案为:28cm.
16.解:如图,梯形ABDC是圆的外切等腰梯形,切点为E、H、G、F;
根据切线长定理可得:AE=AF,BE=BH,DH=DG,CG=CF,
∴C梯形ABDC=2(AB+CD)=4AC,
因此AB+CD=2AC=20cm,
所以梯形ABDC的中位线长MN为10cm.
三.解答题(共6小题,满分56分)
17.(1)答:△OBC是直角三角形.
证明:∵AB、BC、CD分别与⊙O相切于E、F、G,
∴∠OBE=∠OBF=∠EBF,∠OCG=∠OCF=∠GCF,
∵AB∥CD,
∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,
∴△OBC是直角三角形;
(2)解:∵在Rt△BOC中,BO=6,CO=8,
∴BC==10;
(3)解:∵AB、BC、CD分别与⊙O相切于E、F、G,
∴OF⊥BC,
∴OF===4.8.
18.解:设AF=x,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴DA⊥AB,
∴AD是圆的切线,
∵CF是⊙O的切线,E为切点,
∴EF=AF=x,
∴FD=1﹣x,
∵CB⊥AB,
∴CB 为⊙O 的切线,
∴CB=CE,
∴CF=CE+EF=CB+EF=1+x.
∴在Rt△CDF中由勾股定理得到:CF2=CD2+DF2,
即(1+x)2=1+(1﹣x)2,
解得x=,
∴DF=1﹣x=,
∴S△CDF=×1×=.
19.解:(1)∵DA,DC都是圆O的切线,
∴DC=DA,
同理EC=EB,
∵P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B
∴PA=PB,
∴三角形PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=8,
即三角形PDE的周长是8;
(2)连接AB,
∵PA=PB,
∴∠PAB=∠PBA,
∵∠P=40°,
∴∠PAB=∠PBA=(180﹣40)=70°,
∵BF⊥PB,BF为圆直径
∴∠ABF=∠PBF=90°﹣70°=20°
∴∠AFB=90°﹣20°=70°.
答:(1)若PA=4,△PED的周长为8;
(2)若∠P=40°,∠AFB的度数为70°.
20.(1)证明:∵EC、ED都是⊙O的切线,
∴EC=ED,∠ECD=∠EDC.
∵∠EDC+∠EDB=90°,∠ECD+∠B=90°,
∴∠EDB=∠B.
∴ED=BE.
∴DE=BE=EC.
∴DE=BC.
(2)解:在Rt△ABC中,AC=6,BC=8,则AB=10,
根据射影定理可得:
AD=AC2÷AB=3.6,
BD=BC2÷AB=6.4,
∴S△ACD:S△BCD=AD:BD=9:16,
∵ED=EB,EF⊥BD,
∴S△EDF=S△EBD,
同理可得S△EBD=S△BCD,
∴S△EDF=S△BCD,
∴S△ACD:S△EDF=.
21.(1)证明:如图1,连接OB,延长AO交⊙O于点D,
∵PA,PB是⊙O的切线,A,B为切点,
∴∠OBP=∠OAP=90°,
∴∠P+∠AOB=180°,
∵∠AOB+∠BOD=180°,
∴∠BOD=∠P,
∵∠COA=∠P,
∴∠COA=∠BOD,
∵OB=OC,
∴∠BCO=∠CBO,
∵∠COB+2∠BCO=180°,∠COB+2∠COA=180°,
∴∠COA=∠BCO,
∴BC∥OA;
(2)解:如图2,延长BC交PA于点E,过点O作OF⊥BC于F,
∴BF=CF=BC=5,
∵OC=OA=13,
由勾股定理得:AE=OF==12,
∵PA,PB是⊙O的切线,A,B为切点,
∴PA=PB,
设PA=x,则PB=x,PE=x﹣12,
∵BC∥OA,OA⊥PA,
∴BE⊥PA,
∴∠PEB=90°,
∴PB2=PE2+BE2,
∴x2=(x﹣12)2+(13+5)2,
解得:x=,
∴PA=.
22.解:∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴OA⊥AD,OB⊥BC,
∵OA,OB是半径,
∴AF、BP都是⊙O的切线,
又∵PF是⊙O的切线,
∴FE=FA,PE=PB,
∴四边形CDFP的周长为AD+DC+CB=2×3=6
一.选择题(共8小题,满分32分)
1.以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为( )
A.12 B.13 C.14 D.15
2.如图,直角梯形ABCD中,以AD为直径的半圆与BC相切于E,BO交半圆于F,DF的延长线交AB于点P,连DE.以下结论:①DE∥OF;②AB+CD=BC;③PB=PF;④AD2=4AB DC.其中正确的是( )
A.①②③④ B.只有①② C.只有①②④ D.只有③④
3.P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是( )
A.4 B.8 C.12 D.不能确定
4.已知P为⊙O外一点,PA,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=( )
A.35°、145° B.110°、70° C.55°、125° D.110°
5.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为( )
A.5 B.10 C.7.5 D.4
6.如图,⊙O的外切梯形ABCD中,若AD∥BC,那么∠DOC的度数为( )
A.70° B.90° C.60° D.45°
7.如图所示,已知PA、PB切⊙O于A、B两点,C是上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )
A.56° B.60° C.62° D.不可求
8.如图,在平行四边形ABCD中,AB=15,过点D作一圆与AB、BC分别相切于G、H,与边AD、CD相交于点E、F,且5AE=4DE,8CF=DF,则BH等于( )
A.5 B.6 C.7 D.8
二.填空题(共8小题,满分32分)
9.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,则∠CPD= .
10.一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环,当滚到与坡面BC开始相切时停止.其AB=40cm,BC与水平面的夹角为60°.其圆心所经过的路线长是 cm(结果保留根号).
11.如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.
(1)若△PDE的周长为10,则PA的长为 ;
(2)连接CA、CB,若∠P=50°,则∠BCA的度数为 度.
12.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,则CE= .
13.如图,AC是⊙O的直径,PA,PB是⊙O的切线,A,B为切点,AB=6,PA=5.则⊙O的半径 .
14.如图,⊙O外一点P向⊙O引两条切线PA,PB与⊙O相切于点A、B,且PA=PB=10cm,线段CD与⊙O相切于点M.则△PCD的周长是 cm.
15.已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,如果BC边的长为10cm,AD的长为4cm,那么△ABC的周长为 cm.
16.若圆外切等腰梯形的腰长为10cm,则它的中位线长 cm.
三.解答题(共6小题,满分56分)
17.如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.
(1)判断△OBC的形状,并证明你的结论;
(2)求BC的长;
(3)求⊙O的半径OF的长.
18.如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.
19.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是上的任意一点,过点C的切线分别交PA、PB于点D、E.
(1)若PA=4,求△PED的周长;
(2)若∠P=40°,求∠AFB的度数.
20.已知:如图△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,过D作⊙O的切线交BC于点E,EF⊥AB,垂足为F.
(1)求证:DE=BC;
(2)若AC=6,BC=8,求S△ACD:S△EDF的值.
21.如图1,PA,PB是⊙O的切线,A,B为切点,C为上的一点,∠COA=∠P.
(1)求证:BC∥OA;
(2)如图2,若BC=10,OA=13,求PA的长.
22.已知正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点,P不与M和C重合,以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E.求四边形CDFP的周长.
参考答案
一.选择题(共8小题,满分32分)
1.解:设AE的长为x,正方形ABCD的边长为a,
∵CE与半圆O相切于点F,
∴AE=EF,BC=CF,
∵EF+FC+CD+ED=12,
∴AE+ED+CD+BC=12,
∵AD=CD=BC=AB,
∴正方形ABCD的边长为4;
在Rt△CDE中,ED2+CD2=CE2,即(4﹣x)2+42=(4+x)2,解得:x=1,
∵AE+EF+FC+BC+AB=14,
∴直角梯形ABCE周长为14.
故选:C.
2.解:∵BA,BE是圆的切线.
∴AB=BE,BO是△ABE顶角的平分线.
∴OB⊥AE
∵AD是圆的直径.
∴DE⊥AE
∴DE∥OF
故①正确;
∵CD=CE,AB=BE
∴AB+CD=BC
故②正确;
∵OD=OF
∴∠ODF=∠OFD=∠BFP
若PB=PF,则有∠PBF=∠BFP=∠ODF
而△ADP与△ABO不一定相似,故PB=PF不一定成了.
故③不正确;
连接OC.可以证明△OAB∽△CDO
∴
即:OA OD=AB CD
∴AD2=4AB DC
故④正确.
故正确的是:①②④.
故选:C.
3.解:根据题意画出图形,如图所示,
由直线DA和直线DC为圆O的切线,得到AD=DC,同理,由直线EC和直线EB为圆O的切线,得到EC=EB,
又直线PA和直线PB为圆O的切线,所以PA=PB=4,
则△PDE的周长C=PD+DE+PE=PD+DC+EC+PE
=PD+DA+EB+PE=PA+PB=4+4=8.
故选:B.
4.解:如图;连接OA、OB,则∠OAP=∠OBP=90°,
∴∠BOA=180°﹣∠P=110°,
∴∠AEB=∠AOB=55°;
∵四边形AEBF是⊙O的内接四边形,
∴∠AFB=180°﹣∠AEB=125°,
①当C点在优弧AB上运动时,∠BCA=∠AEB=55°;
②当C′点在劣弧AB上运动时,∠BC′A=∠AFB=125°;
故选:C.
5.解:设AF=x,根据切线长定理得AD=x,BD=BE=9﹣x,CE=CF=CA﹣AF=6﹣x,
则有9﹣x+6﹣x=5,解得x=5,即AF的长为5.
故选:A.
6.解:∵DA、CD、CB都与⊙O相切,
∴∠ADO=∠ODC,∠OCD=∠OCB;
∵AD∥BC,
∴∠ADC+∠BCD=180°;
∴∠ODC+∠OCD=(∠ADC+∠BCD)=×180°=90°,即∠DOC=90°;
故选:B.
7.解:∠PMN+∠PNM=180°﹣∠P=124°,
∠AMN+∠BNM=360°﹣124°=236°,
∵MA、MC是⊙O的切线,
∴∠AMO=∠CMO,
∵NB、NC是⊙O的切线,
∴∠BNO=∠CNO,
∴∠CMO+∠CNO=(∠AMN+∠BNM)=118°,
∴∠MON=180°﹣118°=62°,
故选:C.
8.解:由8CF=DF,得CF=15×=,
则CH2=CF×DC,
故CH=5,
设BC=x,则BH=x﹣5=BG,
故AG=20﹣x,
又∵5AE=4DE,
∴DE=x,AE=x,
则AG2=AE×AD,则(20﹣x)2=x2,
解得:x=12,
故BH=BC﹣CH=7.
故选:C.
二.填空题(共8小题,满分32分)
9.解:∵PA=6,⊙O的半径为2,
∴PB=PA﹣AB=6﹣4=2,
∴OP=4,
∵PC、PD切⊙O于点C、D.
∴∠OPC=∠OPD,
∴CO⊥PC,
∴sin∠OPC==,
∴∠OPC=30°,
∴∠CPD=60°,
故答案为:60°.
10.解:连接OD、BD,作DE⊥AB,
∵BC与水平面的夹角为60°,
∴∠DBE=60°,
∴∠BDE=30°,
设BE=x,则BD=2x,
∴由勾股定理得4x2﹣x2=25,
解得x=,
∴OD=AE=40﹣,
故答案为40﹣.
11.解:(1)∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB,DA=DC,EC=EB;
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10;
∴PA=PB=5;
(2)连接OA、OB、AC、BC,在⊙O上取一点F,连接AF、BF,
∵PA、PB分别切⊙O 于A、B;
∴∠PAO=∠PRO=90°
∴∠AOB=360°﹣90°﹣90°﹣50°=130°;
∴∠AFB=∠AOB=65°,
∵∠AFB+∠BCA=180°
∴∠BCA=180°﹣65°=115°;
故答案是:5,115°.
12.解:∵CD、CE分别与⊙O相切于点D、E,
∴CD=CE,
∵∠DAC=∠DCA,
∴AD=CD,
∴AD=CE,
∵AD=2,
∴CE=2.
故答案为:2.
13.解:连接OP,OB,
∵AP为⊙O切线,PB为⊙O切线,
∴PA=PB,
∵∠APO=∠BPO,
PG=PG,
∴△APG≌△BPG,
∴∠PGA=90°,
∵△APO为直角三角形,
∠APG=∠APG,
∴△PGA∽△PAO,
根据垂径定理,得到AG=GB,
在Rt△PAG中,PG==4,
∵△PGA∽△AGO,
∴=,
∴=,
∴AO=.
故答案为:.
14.解:∵CM,CA是圆的切线,
∴CA=CM,
同理,DM=DB,
∴△PCD的周长=PC+PD+CD=PC+CM+DM+PD=PC+CA+PD+BD=PA+PB=20cm.
故答案为:20.
15.解:
∵⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,BC=10cm,AD=4cm,
∴AD=AF=4cm,BE=BD,CF=CE,
即BD+CF=BE+CE=BC=10cm,
∴△ABC的周长是AB+BC+AC=AD+BD+BC+CF+AF=4cm+10cm+10cm+4cm=28cm,
故答案为:28cm.
16.解:如图,梯形ABDC是圆的外切等腰梯形,切点为E、H、G、F;
根据切线长定理可得:AE=AF,BE=BH,DH=DG,CG=CF,
∴C梯形ABDC=2(AB+CD)=4AC,
因此AB+CD=2AC=20cm,
所以梯形ABDC的中位线长MN为10cm.
三.解答题(共6小题,满分56分)
17.(1)答:△OBC是直角三角形.
证明:∵AB、BC、CD分别与⊙O相切于E、F、G,
∴∠OBE=∠OBF=∠EBF,∠OCG=∠OCF=∠GCF,
∵AB∥CD,
∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,
∴△OBC是直角三角形;
(2)解:∵在Rt△BOC中,BO=6,CO=8,
∴BC==10;
(3)解:∵AB、BC、CD分别与⊙O相切于E、F、G,
∴OF⊥BC,
∴OF===4.8.
18.解:设AF=x,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴DA⊥AB,
∴AD是圆的切线,
∵CF是⊙O的切线,E为切点,
∴EF=AF=x,
∴FD=1﹣x,
∵CB⊥AB,
∴CB 为⊙O 的切线,
∴CB=CE,
∴CF=CE+EF=CB+EF=1+x.
∴在Rt△CDF中由勾股定理得到:CF2=CD2+DF2,
即(1+x)2=1+(1﹣x)2,
解得x=,
∴DF=1﹣x=,
∴S△CDF=×1×=.
19.解:(1)∵DA,DC都是圆O的切线,
∴DC=DA,
同理EC=EB,
∵P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B
∴PA=PB,
∴三角形PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=8,
即三角形PDE的周长是8;
(2)连接AB,
∵PA=PB,
∴∠PAB=∠PBA,
∵∠P=40°,
∴∠PAB=∠PBA=(180﹣40)=70°,
∵BF⊥PB,BF为圆直径
∴∠ABF=∠PBF=90°﹣70°=20°
∴∠AFB=90°﹣20°=70°.
答:(1)若PA=4,△PED的周长为8;
(2)若∠P=40°,∠AFB的度数为70°.
20.(1)证明:∵EC、ED都是⊙O的切线,
∴EC=ED,∠ECD=∠EDC.
∵∠EDC+∠EDB=90°,∠ECD+∠B=90°,
∴∠EDB=∠B.
∴ED=BE.
∴DE=BE=EC.
∴DE=BC.
(2)解:在Rt△ABC中,AC=6,BC=8,则AB=10,
根据射影定理可得:
AD=AC2÷AB=3.6,
BD=BC2÷AB=6.4,
∴S△ACD:S△BCD=AD:BD=9:16,
∵ED=EB,EF⊥BD,
∴S△EDF=S△EBD,
同理可得S△EBD=S△BCD,
∴S△EDF=S△BCD,
∴S△ACD:S△EDF=.
21.(1)证明:如图1,连接OB,延长AO交⊙O于点D,
∵PA,PB是⊙O的切线,A,B为切点,
∴∠OBP=∠OAP=90°,
∴∠P+∠AOB=180°,
∵∠AOB+∠BOD=180°,
∴∠BOD=∠P,
∵∠COA=∠P,
∴∠COA=∠BOD,
∵OB=OC,
∴∠BCO=∠CBO,
∵∠COB+2∠BCO=180°,∠COB+2∠COA=180°,
∴∠COA=∠BCO,
∴BC∥OA;
(2)解:如图2,延长BC交PA于点E,过点O作OF⊥BC于F,
∴BF=CF=BC=5,
∵OC=OA=13,
由勾股定理得:AE=OF==12,
∵PA,PB是⊙O的切线,A,B为切点,
∴PA=PB,
设PA=x,则PB=x,PE=x﹣12,
∵BC∥OA,OA⊥PA,
∴BE⊥PA,
∴∠PEB=90°,
∴PB2=PE2+BE2,
∴x2=(x﹣12)2+(13+5)2,
解得:x=,
∴PA=.
22.解:∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴OA⊥AD,OB⊥BC,
∵OA,OB是半径,
∴AF、BP都是⊙O的切线,
又∵PF是⊙O的切线,
∴FE=FA,PE=PB,
∴四边形CDFP的周长为AD+DC+CB=2×3=6
