2021-2022学年北师大版九年级数学下册第3章圆 单元同步达标测评(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第3章圆 单元同步达标测评(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 535.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《第3章圆》单元同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.平面内有两点P,O,⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是( )
A.圆内 B.圆上 C.圆外 D.圆上或圆外
2.如图,A、B、C是⊙O上的点,∠AOB=130°,则∠ACB的大小为( )度.
A.100° B.110° C.115° D.125°
3.下列说法正确的是( )
A.经过三点可以作一个圆 B.三角形的外心是三个内角平分线的交点
C.相等的圆心角所对的弧相等 D.等弧所对的圆心角相等
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=20,CD=16,则BE的长为( )
A.2 B.4 C.5 D.6
5.以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.2
6.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D,且DC+DA=12,⊙O的直径为20,则AB的长等于( )
A.8 B.12 C.16 D.18
7.如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,﹣3).则△ABC的外心坐标应是( )
A.(0,0) B.(1,0) C.(2,﹣1) D.(﹣2,﹣1)
8.如图,在平面直角坐标系中,点A,B的坐标分别为(2,0),(0,4),过A、O、B三点作圆,点C在第一象限部分的圆上运动,连结CO,过点O作CO的垂线交CB的延长线于点D,下列说法:①∠AOC=∠BOD;②tan∠ODB=;③CD的最大值为10.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
9.如图,⊙O是△ABC的外接圆,AB=BC=4,把弧AB沿弦AB向下折叠交BC于点D,若点D为BC中点,则AC长为( )
A.1 B.2 C.2 D.
10.如图,⊙O的直径AB⊥弦CD于E,若CD=8,BD=2,则AB的长为( )
A.2 B.10 C.12 D.5
二.填空题(共10小题,满分30分)
11.如图,△ABC内接于⊙O,OD⊥BC于D,∠A=40°,则∠COD= .
12.如图,已知在半径为1的半⊙O中,CD为直径,A为半圆上一动点,连结OA,作OB平分∠AOC交圆于点B,连结BD,分别与AC,AO交于点N,M.若AM=AN,则△AMD的面积为 .
13.已知⊙O半径为1,AB、BC是⊙O的弦,且AB=1、BC=,则∠ABC的度数是 .
14.已知半径为2cm的扇形的面积为6cm2,则扇形的弧长是 cm.
15.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,则PM的范围是 .
16.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.点P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段BP长的最小值是 .
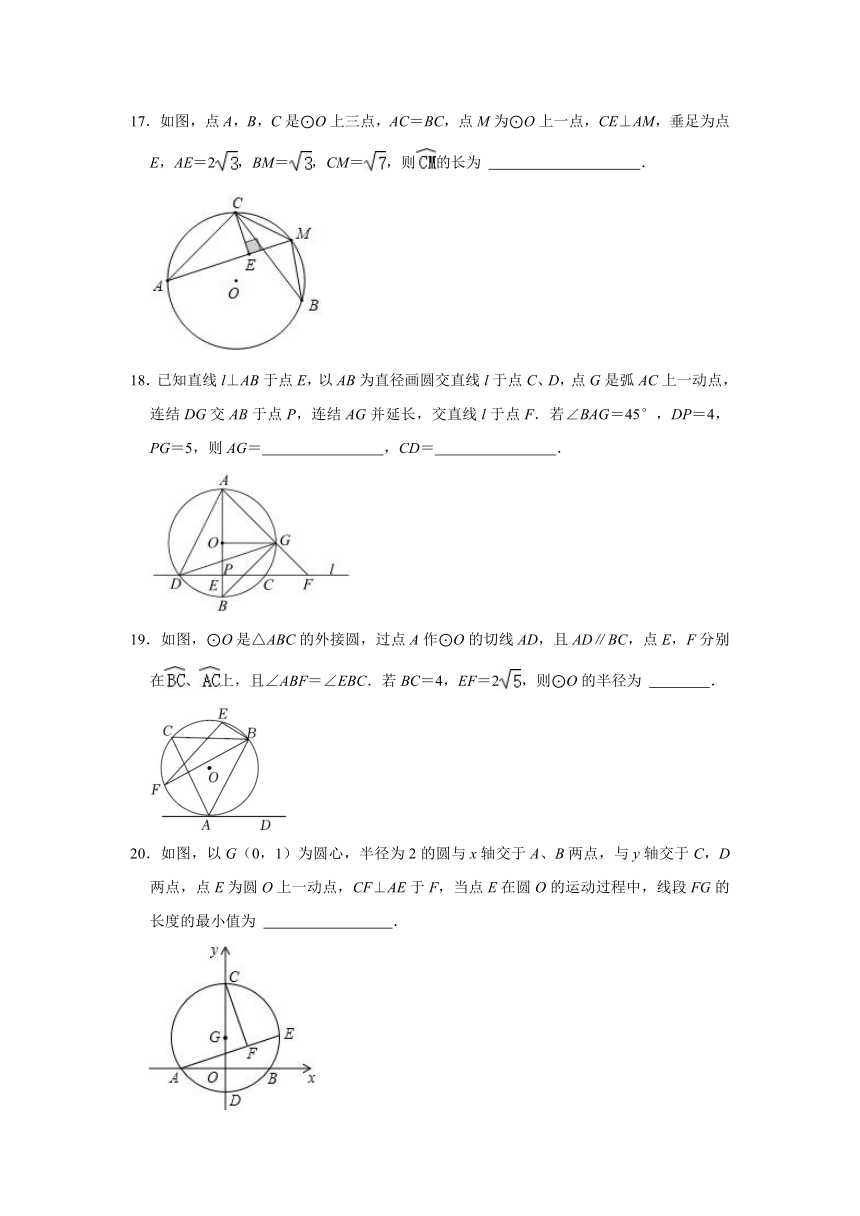
17.如图,点A,B,C是⊙O上三点,AC=BC,点M为⊙O上一点,CE⊥AM,垂足为点E,AE=2,BM=,CM=,则的长为 .
18.已知直线l⊥AB于点E,以AB为直径画圆交直线l于点C、D,点G是弧AC上一动点,连结DG交AB于点P,连结AG并延长,交直线l于点F.若∠BAG=45°,DP=4,PG=5,则AG= ,CD= .
19.如图,⊙O是△ABC的外接圆,过点A作⊙O的切线AD,且AD∥BC,点E,F分别在、上,且∠ABF=∠EBC.若BC=4,EF=2,则⊙O的半径为 .
20.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为圆O上一动点,CF⊥AE于F,当点E在圆O的运动过程中,线段FG的长度的最小值为 .
三.解答题(共6小题,满分60分)
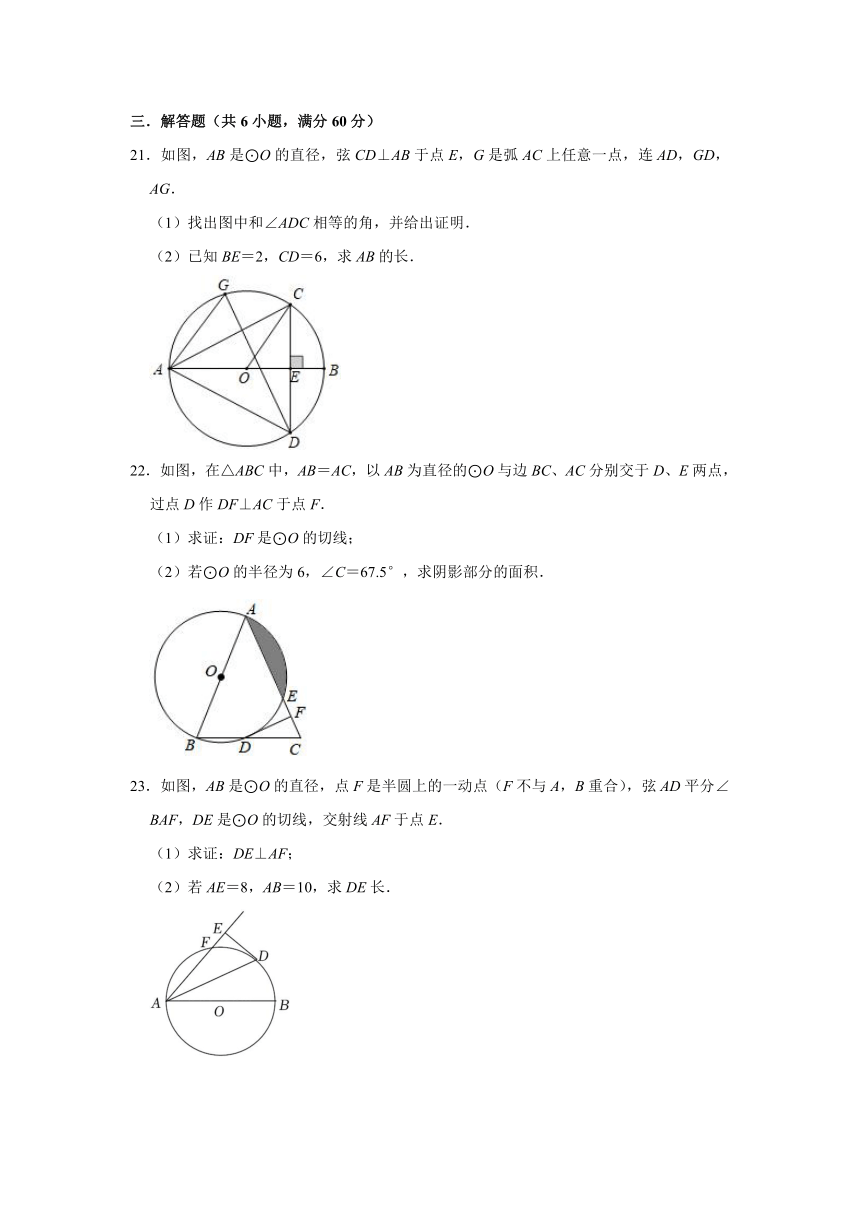
21.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,连AD,GD,AG.
(1)找出图中和∠ADC相等的角,并给出证明.
(2)已知BE=2,CD=6,求AB的长.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为6,∠C=67.5°,求阴影部分的面积.
23.如图,AB是⊙O的直径,点F是半圆上的一动点(F不与A,B重合),弦AD平分∠BAF,DE是⊙O的切线,交射线AF于点E.
(1)求证:DE⊥AF;
(2)若AE=8,AB=10,求DE长.
24.如图,四边形APBC内接于圆,∠APC=60°,AB=AC,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若AP=3,BP=2,求PC的长;
(3)若∠PAC=90°,AB=2,求PD的长.
25.如图,四边形ABCD是⊙O的内接四边形,AC⊥BD,OF⊥AB,垂足分别是E、F.
(1)直接写出OF与CD的数量关系 ,并证明你的结论.
(2)若AB=2,CD=1.求⊙O的半径.
26.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC.
(2)求证:△AFO≌△CEB.
(3)若EB=5cm,设OE=x,求x值及阴影部分的面积.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵⊙O的半径为5,若PO=4,
∴4<5,
∴点P与⊙O的位置关系是点P在⊙O内,
故选:A.
2.解:如图,在优弧AB上取一点D,连接AD,DB.
∵∠ADB=∠AOB,∠AOB=130°,
∴∠ADB=65°,
∵∠ACB+∠ADB=180°,
∴∠ACB=115°,
故选:C.
3.解:A、经过不共线的三点可以作一个圆,所以A选项的说法错误;
B、三角形的外心到三个顶点的距离相等,所以B选项的说法错误;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以选项C说法错误;
D、等弧所对的圆心角相等,所以D选项的说法正确;
故选:D.
4.解:∵AB是⊙O的直径,弦CD⊥AB于点E,AB=20,
∴CO=OB=10,AB⊥CD,CE=DE=CD,
∵CD=16,
∴CE=8,
在Rt△COE中,OE=,
∴BE=OB﹣OE=10﹣6=4,
故选:B.
5.解:如图1,△ABC为⊙O的内接正三角形,作OM⊥BC于M,连接OB,
∵∠OBC=∠ABC=30°,
∴OM=OB=2;
如图2,四边形ABCD为⊙O的内接正方形,作ON⊥DC于N,连接OD,
∵∠ODC=∠ADC=45°,
∴ON=DN=OD=2;
如图3,六边形ABCDEF为⊙O的内接正六边形,作OH⊥DE于H,连接OE,
∵∠OED=∠FED=60°,
∴EH=OE=2,OH=EH=2,
∴半径为4的圆的内接正三角形、正方形、正六边形的边心距分别为2,2,2,
∵22+(2)2=(2)2,
∴以三条边心距所作的三角形为直角三角形,
∴该三角形的面积=×2×2=2.
故选:D.
6.解:连接OC,过O作OF⊥AB,垂足为F,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠PAE,
∴∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴PB∥OC,
∵CD⊥PA,
∴∠OCD=∠CDA=∠OFD=90°,
∴四边形DCOF为矩形,
∴OC=FD,OF=CD.
∵DC+DA=12,
设AD=x,则OF=CD=12﹣x,
∵⊙O的直径为20,
∴DF=OC=10,
∴AF=10﹣x,
在Rt△AOF中,由勾股定理得AF2+OF2=OA2.
即(10﹣x)2+(12﹣x)2=102,
解得x1=4,x2=18.
∵CD=12﹣x大于0,故x=18舍去,
∴x=4,
∴AD=4,AF=10﹣4=6,
∵OF⊥AB,由垂径定理知,F为AB的中点,
∴AB=2AF=12.
故选:B.
7.解:如图,根据网格点O′即为所求.
∵△ABC的外心即是三角形三边垂直平分线的交点,
∴EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(﹣2,﹣1).
故选:D.
8.解:∵OC⊥OD,BO⊥AO,
∴∠DOC=∠BOA=90°.
∴∠DOB+∠BOC=∠BOC+∠COA=90°,
∴AOC=∠BOD.
∴①正确;
连接AB,如图,
∵点A,B的坐标分别为(2,0),(0,4),
∴OA=2,OB=4.
∵OC⊥OD,BO⊥AO,
∴∠C+∠D=90°,∠OAB+∠OBA=90°.
∵∠C=∠OAB,
∴∠D=∠OBA.
∴tan∠ODB=tan∠OBA==.
∴②正确;
∵tan∠ODB=,
∴OD=2OC.
∴CD==OC.
∵OC是圆的弦,直径是圆中最长的弦,
∴当OC为圆的直径时,CD取得最大值.
∵圆的直径AB==2,
∴CD的最大值为2×=10.
∴③正确.
综上,正确的结论有:①②③,
故选:D.
9.解:如图,连接AD,
∵AB=BC=4,
∴∠ACB=∠BAC,
∵点D为BC中点,
∴BD=CD=2,
∵弧AB沿弦AB向下折叠交BC于点D,
∴=,
∴∠ACB=∠ABD+∠BAD,
∵∠BAC=∠BAD+∠CAD,
∴∠ABD=∠CAD,
又∵∠ACB=∠ACD,
∴△ACD∽△BCA,
∴,
∴,
∴AC=,
故选:C.
10.解:∵AB⊥CD,CD=8,BD=2,
∴DE=CE=4,
∴BE===2,
连接OD,设OD=r,则OE=r﹣2,
在Rt△ODE中,
OD2=OE2+DE2,即r2=(r﹣2)2+42,解得r=5,
∴AB=10.
故选:B.
二.填空题(共10小题,满分30分)
11.解:如图,连接OB,
∵OB=OC,OD⊥BC,
∴∠COD=∠BOD=∠BOC;
∵∠A=40°,且∠A=∠BOC,
∴∠COD=40°,
故答案为:40°.
12.解:如图,
∵OB平分∠AOC,
∴∠AOB=∠COB,
∴=,
∴∠ADB=∠BDC,
∵AM=AN,
∴∠ANM=∠AMN,
又∵∠AMN=∠OMD,
∴∠ANM=∠OMD,
∴△OMD∽△AND,
∴==,∠MOD=∠NAD,
∵CD是直径,
∴∠NAD=90°,
∴∠MOD=90°,
∵OA=OD,
∴∠OAD=45°,
∴AD=OD=,
∴====,
∴=,
∴=,
∴=,
∴S△ADM=×1×1×=.
故答案为:.
13.解:连接OA、OB、OC,
∵⊙O半径为1,
∴OA=OB=OC=1,
∵AB=1,
∴OA=OB=AB,
∴△AOB是等边三角形,
∴∠AOB=60°,
∵OB=OC=1,BC=,
∴OB2+OC2=BC2,
∴△OBC是直角三角形,∠BOC=90°,
分两种情况:
①当AB、BC在OB的同侧时,如图1所示:
则∠AOC=∠BOC﹣∠AOB=30°,
∴∠ABC=∠AOC=15°;
②当AB、BC在OB的异侧时,如图2所示:
则∠AOC=∠BOC+∠AOB=150°,
∴∠ABC=(360°﹣∠AOC)=(360°﹣150°)=105°;
综上所述,∠ABC的度数是15°或105°,
故答案为:15°或105°.
14.解:设扇形的弧长为acm,
∵半径为2cm的扇形的面积为6cm2,
∴=6,
解得:a=6,
即扇形的弧长为6cm,
故答案为:6.
15.解:如图:延长CP交⊙O于N,连接DN.
∵AB⊥CN,
∴CP=PN,
∵CM=DM,
∴PM=DN,
∴当DN为直径时,PM的值最大,最大值为,
当DN=AC时,PM最小,最小值为,
∴PM的范围是≤PM≤.
故答案为:≤PM≤.
16.解:∵∠ACB=90°,
∴∠ACP+∠PCB=90°,
∵∠PAC=∠PCB
∴∠CAP+∠ACP=90°,
∴∠APC=90°,
∴点P在以AC为直径的⊙O上,连接OB交⊙O于点P,此时PB最小,
在Rt△CBO中,∠OCB=90°,BC=3,OC=2,
∴OB===,
∴PB=OB﹣OP=﹣2.
∴PC最小值为﹣2.
故答案为:﹣2.
17.解:在AE上截取AG=BM,连接CG,
∵AC=BC,∠A=∠B,
∴△ACG≌△BCM(SAS),
∴CG=CM=,
∵AE=2,AG=BM=,
∴GE=,
∵CE⊥AM,
∴CE===2,
∴tan∠A==,
∴∠A=30°,
∴∠COM=60°,
连接OM,CO,
∵OC=OM,
∴△COM是等边三角形,
∴OC=,
∴的长==π,
故答案为π.
18.解:连接OD,如图,
∵AB为直径,
∴∠AGB=90°,
∵∠BAG=45°,
∴∠ABG=45°,
∴∠ADG=∠ABG=45°,
∵∠AGP=∠DGA,∠GAP=∠GDA,
∴△GAP∽△GDA,
∴GA:GD=GP:GA,即GA:9=5:GA,
解得GA=3,
∵△ABG为等腰直角三角形,
∴OG⊥AB,
∴OG=AG=×3=,
∵CD⊥AB,
∴DE=CE,OG∥CD,
∴==,
∴DE=OG=×=,
∴CD=2DE=.
故答案为:3,.
19.解:如图,连接AO,并延长交⊙O于H,交BC于N,连接BO,
∵AD是⊙O的切线,AH是直径,
∴OA⊥AD,
∴∠HAB+∠BAD=90°,
∵AH是直径,
∴∠ABH=90°,
∴∠HAB+∠H=90°,
∴∠H=∠BAD,
∵BC∥AD,
∴∠BAD=∠ABC,
∵∠H=∠C,
∴∠C=∠ABC,
∴AC=AB,=,且AH是直径,
∴AN⊥BC,BN=CN=BC=2,
∵∠ABF=∠EBC.
∴∠ABC=∠EBF,
∴=,
∴AC=EF=2,
∴AB=AC=2,
∴AN==4,
设OB=AO=r,
∴r2=(4﹣r)2+22,
∴r=,
∴⊙O的半径为,
故答案为:.
20.解:作GM⊥AC于M,连接AG.
∵GO⊥AB,
∴OA=OB,
在Rt△AGO中,AG=2,OG=1,
∴AG=2OG,OA===,
∴∠GAO=30°,AB=2AO=2,
∴∠AGO=60°,
∵GC=GA,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=2,MG=CG=1,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=﹣1.
故答案为:﹣1.
三.解答题(共6小题,满分60分)
21.解:(1)∠AGD=∠ADC,
理由如下:∵弦CD⊥AB,
∴DE=CE,=,
∴∠AGD=∠ADC,∠ACD=∠ADC;
(2)设OC=OB=r,
∵OB⊥CD,
∴EC=DE=3,
∵OC2=OE2+EC2,
∴R2=(R﹣2)2+32,
∴R=,
∴AB=2R=.
22.(1)证明:如图,连接OD,
∵OD=OB,
∴∠ODB=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC于点F,
∴∠ODF=∠DFC=90°,
∵DF经过⊙O的半径OD的端点D,且DF⊥OD,
∴DF是⊙O的切线.
(2)解:如图,连接OE,则OE=OA,
∵∠B=∠C=67.5°,
∴∠OEA=∠A=180°﹣67.5°﹣67.5°=45°,
∴∠AOE=180°﹣45°﹣45°=90°,
∵OA=OE=6,
∴S阴影==9π﹣18,
∴阴影部分的面积为9π﹣18.
23.(1)证明:如图,连接OD,
∵DE与⊙O相切于点D,
∴DE⊥OD,
∴∠ODE=90°,
∵OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠BAF,
∴∠OAD=∠DAF,
∴∠ODA=∠DAF,
∴OD∥AF,
∴∠AED=180°﹣∠ODE=90°,
∴DE⊥AF.
(2)如图,连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠AED=∠ADB,
∵∠EAD=∠DAB,
∴△AED∽△ADB,
∴,
∵AE=8,AB=10,
∴AD===,
∴DE===4,
∴DE的长为4.
24.(1)证明:∵∠APC=60°,
∴∠ABC=∠APC=60°,
∵AB=AC,
∴△ABC是等边三角形;
(2)解:如图1中,在PC上截取PT,使得PT=PA.
∵∠APT=60°,
∴△APT是等边三角形,
∵△ABC是等边三角形,
∴AP=AT,AB=AC,∠PAT=∠BAC=60°,
∴∠PAB=∠TAC,
∴△PAB≌△TAC(SAS),
∴PB=TC=2,
∵PT=PA=3,
∴PC=PT+CT=3+2=5;
(3)解:在Rt△PAC中,∠APC=60°,∠PAC=90°,AC=AB=2,
∴∠PCA=30°,
∴PC=2PA.
∵PC2=PA2+AC2,
∴PA=2,PC=4.
同理,可求出CD=4,AD=6,
∴PD=AD﹣PA=4.
25.解:(1)结论:OF=CD.
理由:连接AO并延长交⊙O于点G,连接CB.
∵OF⊥AB,
∴AF=BF,
∵AO=GO,
∴OF是△ABG的中位线,
∴OF=BG,
∵AG是⊙O的直径,
∴∠ABG=90°,
∴∠BAG+∠G=90°,
∵AC⊥BD,
∴∠CEB=90°,
∴∠ECB+∠EBC=90°,
∵∠G=∠ECB,
∴∠BAG=∠CBD,
∴∠BAG所对弧上的圆心角等于∠CBD所对弧上的圆心角,
∴BG=CD,
∴OF=CD;
(2)由(1)得:OF=CD=,
在Rt△AOF中,AF=1,
∴OA===,
∴⊙O的半径为.
26.(1)证明:∵AB为⊙O的直径,
∴AC⊥BC,
又∵OF⊥AC,
∴OF∥BC;
(2)证明:∵AB⊥CD,
∴=,
∴∠CAB=∠BCD,
在△AFO和△CEB中,
∴△AFO≌△CEB(AAS);
(3)解:连接DO.设OE=x,
∵OF∥BC,OA=OB,
∴OF=BC,
∵OF=BE=5cm,
∴BC=10cm,
∵△AFO≌△CEB,
∴OA=BC=10cm,
∴CE===5cm,
∴CD=2CE=10cm,
∵OB=x+5,
∴OE=OB﹣5=10﹣5=5cm,
∵cos∠COE===,
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是:=cm2
△COD的面积是:CD OE==25cm2
∴阴影部分的面积是:(﹣25)cm2.
一.选择题(共10小题,满分30分)
1.平面内有两点P,O,⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是( )
A.圆内 B.圆上 C.圆外 D.圆上或圆外
2.如图,A、B、C是⊙O上的点,∠AOB=130°,则∠ACB的大小为( )度.
A.100° B.110° C.115° D.125°
3.下列说法正确的是( )
A.经过三点可以作一个圆 B.三角形的外心是三个内角平分线的交点
C.相等的圆心角所对的弧相等 D.等弧所对的圆心角相等
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=20,CD=16,则BE的长为( )
A.2 B.4 C.5 D.6
5.以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.2
6.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D,且DC+DA=12,⊙O的直径为20,则AB的长等于( )
A.8 B.12 C.16 D.18
7.如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,﹣3).则△ABC的外心坐标应是( )
A.(0,0) B.(1,0) C.(2,﹣1) D.(﹣2,﹣1)
8.如图,在平面直角坐标系中,点A,B的坐标分别为(2,0),(0,4),过A、O、B三点作圆,点C在第一象限部分的圆上运动,连结CO,过点O作CO的垂线交CB的延长线于点D,下列说法:①∠AOC=∠BOD;②tan∠ODB=;③CD的最大值为10.其中正确的是( )
A.①② B.①③ C.②③ D.①②③
9.如图,⊙O是△ABC的外接圆,AB=BC=4,把弧AB沿弦AB向下折叠交BC于点D,若点D为BC中点,则AC长为( )
A.1 B.2 C.2 D.
10.如图,⊙O的直径AB⊥弦CD于E,若CD=8,BD=2,则AB的长为( )
A.2 B.10 C.12 D.5
二.填空题(共10小题,满分30分)
11.如图,△ABC内接于⊙O,OD⊥BC于D,∠A=40°,则∠COD= .
12.如图,已知在半径为1的半⊙O中,CD为直径,A为半圆上一动点,连结OA,作OB平分∠AOC交圆于点B,连结BD,分别与AC,AO交于点N,M.若AM=AN,则△AMD的面积为 .
13.已知⊙O半径为1,AB、BC是⊙O的弦,且AB=1、BC=,则∠ABC的度数是 .
14.已知半径为2cm的扇形的面积为6cm2,则扇形的弧长是 cm.
15.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,则PM的范围是 .
16.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.点P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段BP长的最小值是 .
17.如图,点A,B,C是⊙O上三点,AC=BC,点M为⊙O上一点,CE⊥AM,垂足为点E,AE=2,BM=,CM=,则的长为 .
18.已知直线l⊥AB于点E,以AB为直径画圆交直线l于点C、D,点G是弧AC上一动点,连结DG交AB于点P,连结AG并延长,交直线l于点F.若∠BAG=45°,DP=4,PG=5,则AG= ,CD= .
19.如图,⊙O是△ABC的外接圆,过点A作⊙O的切线AD,且AD∥BC,点E,F分别在、上,且∠ABF=∠EBC.若BC=4,EF=2,则⊙O的半径为 .
20.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为圆O上一动点,CF⊥AE于F,当点E在圆O的运动过程中,线段FG的长度的最小值为 .
三.解答题(共6小题,满分60分)
21.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,连AD,GD,AG.
(1)找出图中和∠ADC相等的角,并给出证明.
(2)已知BE=2,CD=6,求AB的长.
22.如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为6,∠C=67.5°,求阴影部分的面积.
23.如图,AB是⊙O的直径,点F是半圆上的一动点(F不与A,B重合),弦AD平分∠BAF,DE是⊙O的切线,交射线AF于点E.
(1)求证:DE⊥AF;
(2)若AE=8,AB=10,求DE长.
24.如图,四边形APBC内接于圆,∠APC=60°,AB=AC,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若AP=3,BP=2,求PC的长;
(3)若∠PAC=90°,AB=2,求PD的长.
25.如图,四边形ABCD是⊙O的内接四边形,AC⊥BD,OF⊥AB,垂足分别是E、F.
(1)直接写出OF与CD的数量关系 ,并证明你的结论.
(2)若AB=2,CD=1.求⊙O的半径.
26.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC.
(2)求证:△AFO≌△CEB.
(3)若EB=5cm,设OE=x,求x值及阴影部分的面积.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵⊙O的半径为5,若PO=4,
∴4<5,
∴点P与⊙O的位置关系是点P在⊙O内,
故选:A.
2.解:如图,在优弧AB上取一点D,连接AD,DB.
∵∠ADB=∠AOB,∠AOB=130°,
∴∠ADB=65°,
∵∠ACB+∠ADB=180°,
∴∠ACB=115°,
故选:C.
3.解:A、经过不共线的三点可以作一个圆,所以A选项的说法错误;
B、三角形的外心到三个顶点的距离相等,所以B选项的说法错误;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以选项C说法错误;
D、等弧所对的圆心角相等,所以D选项的说法正确;
故选:D.
4.解:∵AB是⊙O的直径,弦CD⊥AB于点E,AB=20,
∴CO=OB=10,AB⊥CD,CE=DE=CD,
∵CD=16,
∴CE=8,
在Rt△COE中,OE=,
∴BE=OB﹣OE=10﹣6=4,
故选:B.
5.解:如图1,△ABC为⊙O的内接正三角形,作OM⊥BC于M,连接OB,
∵∠OBC=∠ABC=30°,
∴OM=OB=2;
如图2,四边形ABCD为⊙O的内接正方形,作ON⊥DC于N,连接OD,
∵∠ODC=∠ADC=45°,
∴ON=DN=OD=2;
如图3,六边形ABCDEF为⊙O的内接正六边形,作OH⊥DE于H,连接OE,
∵∠OED=∠FED=60°,
∴EH=OE=2,OH=EH=2,
∴半径为4的圆的内接正三角形、正方形、正六边形的边心距分别为2,2,2,
∵22+(2)2=(2)2,
∴以三条边心距所作的三角形为直角三角形,
∴该三角形的面积=×2×2=2.
故选:D.
6.解:连接OC,过O作OF⊥AB,垂足为F,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠PAE,
∴∠DAC=∠CAO,
∴∠DAC=∠OCA,
∴PB∥OC,
∵CD⊥PA,
∴∠OCD=∠CDA=∠OFD=90°,
∴四边形DCOF为矩形,
∴OC=FD,OF=CD.
∵DC+DA=12,
设AD=x,则OF=CD=12﹣x,
∵⊙O的直径为20,
∴DF=OC=10,
∴AF=10﹣x,
在Rt△AOF中,由勾股定理得AF2+OF2=OA2.
即(10﹣x)2+(12﹣x)2=102,
解得x1=4,x2=18.
∵CD=12﹣x大于0,故x=18舍去,
∴x=4,
∴AD=4,AF=10﹣4=6,
∵OF⊥AB,由垂径定理知,F为AB的中点,
∴AB=2AF=12.
故选:B.
7.解:如图,根据网格点O′即为所求.
∵△ABC的外心即是三角形三边垂直平分线的交点,
∴EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(﹣2,﹣1).
故选:D.
8.解:∵OC⊥OD,BO⊥AO,
∴∠DOC=∠BOA=90°.
∴∠DOB+∠BOC=∠BOC+∠COA=90°,
∴AOC=∠BOD.
∴①正确;
连接AB,如图,
∵点A,B的坐标分别为(2,0),(0,4),
∴OA=2,OB=4.
∵OC⊥OD,BO⊥AO,
∴∠C+∠D=90°,∠OAB+∠OBA=90°.
∵∠C=∠OAB,
∴∠D=∠OBA.
∴tan∠ODB=tan∠OBA==.
∴②正确;
∵tan∠ODB=,
∴OD=2OC.
∴CD==OC.
∵OC是圆的弦,直径是圆中最长的弦,
∴当OC为圆的直径时,CD取得最大值.
∵圆的直径AB==2,
∴CD的最大值为2×=10.
∴③正确.
综上,正确的结论有:①②③,
故选:D.
9.解:如图,连接AD,
∵AB=BC=4,
∴∠ACB=∠BAC,
∵点D为BC中点,
∴BD=CD=2,
∵弧AB沿弦AB向下折叠交BC于点D,
∴=,
∴∠ACB=∠ABD+∠BAD,
∵∠BAC=∠BAD+∠CAD,
∴∠ABD=∠CAD,
又∵∠ACB=∠ACD,
∴△ACD∽△BCA,
∴,
∴,
∴AC=,
故选:C.
10.解:∵AB⊥CD,CD=8,BD=2,
∴DE=CE=4,
∴BE===2,
连接OD,设OD=r,则OE=r﹣2,
在Rt△ODE中,
OD2=OE2+DE2,即r2=(r﹣2)2+42,解得r=5,
∴AB=10.
故选:B.
二.填空题(共10小题,满分30分)
11.解:如图,连接OB,
∵OB=OC,OD⊥BC,
∴∠COD=∠BOD=∠BOC;
∵∠A=40°,且∠A=∠BOC,
∴∠COD=40°,
故答案为:40°.
12.解:如图,
∵OB平分∠AOC,
∴∠AOB=∠COB,
∴=,
∴∠ADB=∠BDC,
∵AM=AN,
∴∠ANM=∠AMN,
又∵∠AMN=∠OMD,
∴∠ANM=∠OMD,
∴△OMD∽△AND,
∴==,∠MOD=∠NAD,
∵CD是直径,
∴∠NAD=90°,
∴∠MOD=90°,
∵OA=OD,
∴∠OAD=45°,
∴AD=OD=,
∴====,
∴=,
∴=,
∴=,
∴S△ADM=×1×1×=.
故答案为:.
13.解:连接OA、OB、OC,
∵⊙O半径为1,
∴OA=OB=OC=1,
∵AB=1,
∴OA=OB=AB,
∴△AOB是等边三角形,
∴∠AOB=60°,
∵OB=OC=1,BC=,
∴OB2+OC2=BC2,
∴△OBC是直角三角形,∠BOC=90°,
分两种情况:
①当AB、BC在OB的同侧时,如图1所示:
则∠AOC=∠BOC﹣∠AOB=30°,
∴∠ABC=∠AOC=15°;
②当AB、BC在OB的异侧时,如图2所示:
则∠AOC=∠BOC+∠AOB=150°,
∴∠ABC=(360°﹣∠AOC)=(360°﹣150°)=105°;
综上所述,∠ABC的度数是15°或105°,
故答案为:15°或105°.
14.解:设扇形的弧长为acm,
∵半径为2cm的扇形的面积为6cm2,
∴=6,
解得:a=6,
即扇形的弧长为6cm,
故答案为:6.
15.解:如图:延长CP交⊙O于N,连接DN.
∵AB⊥CN,
∴CP=PN,
∵CM=DM,
∴PM=DN,
∴当DN为直径时,PM的值最大,最大值为,
当DN=AC时,PM最小,最小值为,
∴PM的范围是≤PM≤.
故答案为:≤PM≤.
16.解:∵∠ACB=90°,
∴∠ACP+∠PCB=90°,
∵∠PAC=∠PCB
∴∠CAP+∠ACP=90°,
∴∠APC=90°,
∴点P在以AC为直径的⊙O上,连接OB交⊙O于点P,此时PB最小,
在Rt△CBO中,∠OCB=90°,BC=3,OC=2,
∴OB===,
∴PB=OB﹣OP=﹣2.
∴PC最小值为﹣2.
故答案为:﹣2.
17.解:在AE上截取AG=BM,连接CG,
∵AC=BC,∠A=∠B,
∴△ACG≌△BCM(SAS),
∴CG=CM=,
∵AE=2,AG=BM=,
∴GE=,
∵CE⊥AM,
∴CE===2,
∴tan∠A==,
∴∠A=30°,
∴∠COM=60°,
连接OM,CO,
∵OC=OM,
∴△COM是等边三角形,
∴OC=,
∴的长==π,
故答案为π.
18.解:连接OD,如图,
∵AB为直径,
∴∠AGB=90°,
∵∠BAG=45°,
∴∠ABG=45°,
∴∠ADG=∠ABG=45°,
∵∠AGP=∠DGA,∠GAP=∠GDA,
∴△GAP∽△GDA,
∴GA:GD=GP:GA,即GA:9=5:GA,
解得GA=3,
∵△ABG为等腰直角三角形,
∴OG⊥AB,
∴OG=AG=×3=,
∵CD⊥AB,
∴DE=CE,OG∥CD,
∴==,
∴DE=OG=×=,
∴CD=2DE=.
故答案为:3,.
19.解:如图,连接AO,并延长交⊙O于H,交BC于N,连接BO,
∵AD是⊙O的切线,AH是直径,
∴OA⊥AD,
∴∠HAB+∠BAD=90°,
∵AH是直径,
∴∠ABH=90°,
∴∠HAB+∠H=90°,
∴∠H=∠BAD,
∵BC∥AD,
∴∠BAD=∠ABC,
∵∠H=∠C,
∴∠C=∠ABC,
∴AC=AB,=,且AH是直径,
∴AN⊥BC,BN=CN=BC=2,
∵∠ABF=∠EBC.
∴∠ABC=∠EBF,
∴=,
∴AC=EF=2,
∴AB=AC=2,
∴AN==4,
设OB=AO=r,
∴r2=(4﹣r)2+22,
∴r=,
∴⊙O的半径为,
故答案为:.
20.解:作GM⊥AC于M,连接AG.
∵GO⊥AB,
∴OA=OB,
在Rt△AGO中,AG=2,OG=1,
∴AG=2OG,OA===,
∴∠GAO=30°,AB=2AO=2,
∴∠AGO=60°,
∵GC=GA,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=2,MG=CG=1,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=﹣1.
故答案为:﹣1.
三.解答题(共6小题,满分60分)
21.解:(1)∠AGD=∠ADC,
理由如下:∵弦CD⊥AB,
∴DE=CE,=,
∴∠AGD=∠ADC,∠ACD=∠ADC;
(2)设OC=OB=r,
∵OB⊥CD,
∴EC=DE=3,
∵OC2=OE2+EC2,
∴R2=(R﹣2)2+32,
∴R=,
∴AB=2R=.
22.(1)证明:如图,连接OD,
∵OD=OB,
∴∠ODB=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC于点F,
∴∠ODF=∠DFC=90°,
∵DF经过⊙O的半径OD的端点D,且DF⊥OD,
∴DF是⊙O的切线.
(2)解:如图,连接OE,则OE=OA,
∵∠B=∠C=67.5°,
∴∠OEA=∠A=180°﹣67.5°﹣67.5°=45°,
∴∠AOE=180°﹣45°﹣45°=90°,
∵OA=OE=6,
∴S阴影==9π﹣18,
∴阴影部分的面积为9π﹣18.
23.(1)证明:如图,连接OD,
∵DE与⊙O相切于点D,
∴DE⊥OD,
∴∠ODE=90°,
∵OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠BAF,
∴∠OAD=∠DAF,
∴∠ODA=∠DAF,
∴OD∥AF,
∴∠AED=180°﹣∠ODE=90°,
∴DE⊥AF.
(2)如图,连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠AED=∠ADB,
∵∠EAD=∠DAB,
∴△AED∽△ADB,
∴,
∵AE=8,AB=10,
∴AD===,
∴DE===4,
∴DE的长为4.
24.(1)证明:∵∠APC=60°,
∴∠ABC=∠APC=60°,
∵AB=AC,
∴△ABC是等边三角形;
(2)解:如图1中,在PC上截取PT,使得PT=PA.
∵∠APT=60°,
∴△APT是等边三角形,
∵△ABC是等边三角形,
∴AP=AT,AB=AC,∠PAT=∠BAC=60°,
∴∠PAB=∠TAC,
∴△PAB≌△TAC(SAS),
∴PB=TC=2,
∵PT=PA=3,
∴PC=PT+CT=3+2=5;
(3)解:在Rt△PAC中,∠APC=60°,∠PAC=90°,AC=AB=2,
∴∠PCA=30°,
∴PC=2PA.
∵PC2=PA2+AC2,
∴PA=2,PC=4.
同理,可求出CD=4,AD=6,
∴PD=AD﹣PA=4.
25.解:(1)结论:OF=CD.
理由:连接AO并延长交⊙O于点G,连接CB.
∵OF⊥AB,
∴AF=BF,
∵AO=GO,
∴OF是△ABG的中位线,
∴OF=BG,
∵AG是⊙O的直径,
∴∠ABG=90°,
∴∠BAG+∠G=90°,
∵AC⊥BD,
∴∠CEB=90°,
∴∠ECB+∠EBC=90°,
∵∠G=∠ECB,
∴∠BAG=∠CBD,
∴∠BAG所对弧上的圆心角等于∠CBD所对弧上的圆心角,
∴BG=CD,
∴OF=CD;
(2)由(1)得:OF=CD=,
在Rt△AOF中,AF=1,
∴OA===,
∴⊙O的半径为.
26.(1)证明:∵AB为⊙O的直径,
∴AC⊥BC,
又∵OF⊥AC,
∴OF∥BC;
(2)证明:∵AB⊥CD,
∴=,
∴∠CAB=∠BCD,
在△AFO和△CEB中,
∴△AFO≌△CEB(AAS);
(3)解:连接DO.设OE=x,
∵OF∥BC,OA=OB,
∴OF=BC,
∵OF=BE=5cm,
∴BC=10cm,
∵△AFO≌△CEB,
∴OA=BC=10cm,
∴CE===5cm,
∴CD=2CE=10cm,
∵OB=x+5,
∴OE=OB﹣5=10﹣5=5cm,
∵cos∠COE===,
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是:=cm2
△COD的面积是:CD OE==25cm2
∴阴影部分的面积是:(﹣25)cm2.
