2021-2022学年鲁教版(五四制)六年级数学上册第4章一元一次方程 同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册第4章一元一次方程 同步练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 164.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:53:06 | ||
图片预览




文档简介
2021-2022学年鲁教版六年级数学上册《第4章一元一次方程》同步综合练习题(附答案)
1.在①2x+1;②1+7=15﹣8+1;③;④x+2y=3中,方程共有( )
A.1个 B.2个 C.3个 D.4个
2.下列所给条件,不能列出方程的是( )
A.某数比它的平方小6
B.某数加上3,再乘以2等于14
C.某数与它的的差
D.某数的3倍与7的和等于29
3.下列各判断句中,错误的是( )
A.方程是等式,但等式不一定是方程
B.由ax=ay这个条件不能得到x=y一定成立的结论
C.在整数范围内,方程6x=3无解
D.x5=0不是方程
4.若x=1是ax+2x=3方程的解,则a的值是( )
A.﹣1 B.1 C.﹣3 D.3
5.下列方程变形正确的是( )
A.2x﹣5=5x+4变形为2x﹣5=5x+4﹣5x﹣4
B.x=2变形为x=2×=1
C.4x﹣8=0变形为(4x﹣8+8)=8×
D.﹣=1变形为3(x﹣1)﹣2=1
6.下列方程的变形,符合等式性质的是( )
A.由x=0,得x=2 B.由x﹣3=5,得x=5﹣3
C.﹣3x=,得x=﹣ D.由x+2=4,得x=4﹣2
7.若x=0是方程的解,则k值为( )
A.0 B.2 C.3 D.4
8.已知k=,则满足k为整数的所有整数x的和是( )
A.﹣1 B.0 C.1 D.2
9.某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,设原计划每小时生产x个零件,则所列方程为( )
A.13x=12(x+10)+60 B.12(x+10)=13x+60
C. D.
10.《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,所列方程正确的是( )
A.5x﹣45=7x﹣3 B.5x+45=7x+3 C.= D.=
11.已知关于x的一元一次方程mx﹣1=2(x+)的解是正整数,则整数m的值为 .
12.已知关于x的方程(m+3)x|m+4|+18=0是一元一次方程,则m的值为 .
13.方程|x|=ax+2有且仅有一个负数根,则a的取值范围是 .
14.已知方程的解也是方程|3x﹣2|=b的解,则b= .
15.一艘船在水中航行,已知该船在静水中的速度为m(千米/小时),水流速度为n(千米/小时),如果该船从码头A出发,先顺流航行5小时,然后又调头逆流航行了5小时,那么最后船离A码头 千米.
16.小颖按如图所示的程序输入一个正数x,最后从输出端得到的数为16,求小颖输入的数x的值 .
17.解下列方程:
(1)﹣3x﹣6=9 (2)5﹣4x=﹣6x+7
(3)2(x﹣1)+2=4x﹣6 (4)=1.
18.解下列方程
(1)10x+7=12x﹣5 (2)1﹣=.
19.若关于x的方程|x﹣2|+|x+1|=a有四个整数解,求a的取值范围.
20.已知关于x的方程4x+2m=3x+1与方程3x+2m=6x+1的解相同;
(1)求m的值;
(2)求代数式(﹣2m)3﹣(m﹣)4的值.
21.某车间有工人85人,平均每人每天可加工大齿轮16个或小齿轮10个,又知2个大齿轮和3个小齿轮配套,问应安排多少个工人生产大齿轮使生产的产品刚好成套?
22.如图,在数轴上,点A在原点O的左侧,点B在原点O的右侧,点A所对应的数a满足|a+1|=0,且AB=12,点D从A出发以1个单位长度/秒的速度沿数轴向右运动,点E从B出发以2个单位长度/秒的速度沿数轴向左运动,当D、E两点相遇时停止运动.
(1)直接写出点A表示的数为 ,点B表示的数为 ;
(2)点P为线段DE的中点,D、E两点同时开始运动,设运动时间为t秒,线段OP的长为d个单位长度,求用含t的整式表示d;
(3)在(2)条件下,点C在线段AB上,且AC=2BC,当t为何值时,满足2OP+3CE=CD.
23.某牛奶加工厂现有鲜奶8吨,若市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润2000元.该工厂的生产能力是:如制成酸奶每天可加工3吨;制成奶片每天可加工1吨.受人员制约,两种加工方式不可同时进行;受气温制约,这批牛奶必须在4天内全部销售或加工完毕.为此,该工厂设计了两种可行方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多?为什么?
24.据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见表:若2015年5月份,该市居民甲用电100度,交电费60元.
一户居民一个月用电量的范围 电费价格(单位:元/度)
不超过150度 a
超过150度但不超过300度的部分 0.65
超过300度的部分 0.9
(1)表中,a= ;若居民乙用电200度,则应交电费 元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度0.62元?
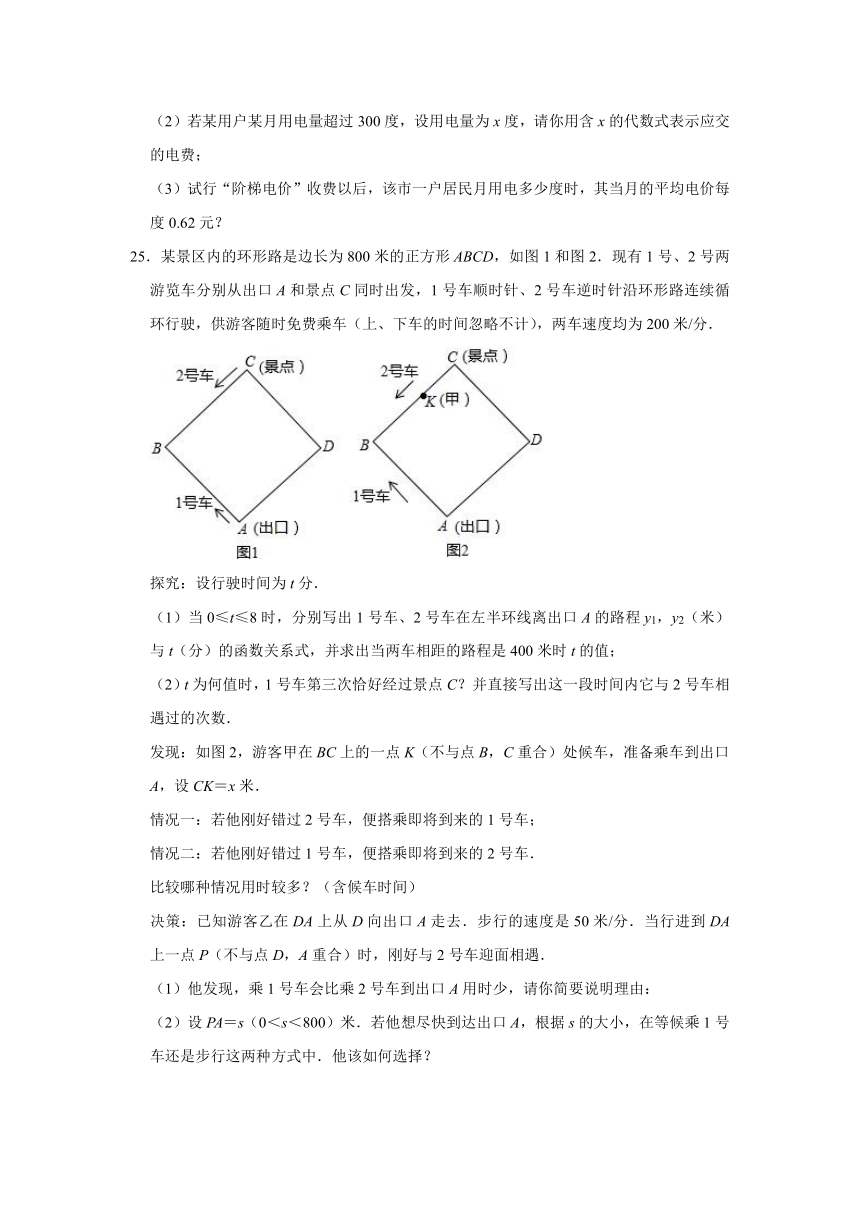
25.某景区内的环形路是边长为800米的正方形ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
探究:设行驶时间为t分.
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y1,y2(米)与t(分)的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇过的次数.
发现:如图2,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多?(含候车时间)
决策:已知游客乙在DA上从D向出口A走去.步行的速度是50米/分.当行进到DA上一点P(不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由:
(2)设PA=s(0<s<800)米.若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中.他该如何选择?
参考答案
1.解:(1)2x+1,含未知数但不是等式,所以不是方程.
(2)1+7=15﹣8+1,是等式但不含未知数,所以不是方程.
(3),是含有未知数的等式,所以是方程.
(4)x+2y=3,是含有未知数的等式,所以是方程.
故有所有式子中有2个是方程.
故选:B.
2.解:设某数为x,
A、x2﹣x=6,是方程,故本选项错误;
B、2(x+3)=14,是方程,故本选项错误;
C、x﹣x,不是方程,故本选项正确;
D、3x+7=29,是方程,故本选项错误.
故选:C.
3.解:A、方程是含有未知数的等式,而等式中不一定含有未知数,所以“方程是等式,但等式不一定是方程”这种说法正确.故本选项不符合题意;
B、当a=0时,等式ax=ay恒成立,但是x不一定与y相等,所以“由ax=ay这个条件不能得到x=y一定成立的结论”这种说法正确.故本选项不符合题意;
C、方程6x=3的解是x=,不是整数,所以“在整数范围内,方程6x=3无解”这种说法正确.故本选项不符合题意;
D、x5=0是含有未知数的等式,所以它是方程.故本选项符合题意.
故选:D.
4.解:根据题意,将x=1代入方程ax+2x=3,
得:a+2=3,
得:a=1.
故选:B.
5.解:A.2x﹣5=5x+4变形为2x﹣5﹣5x﹣4=5x+4﹣5x﹣4,即A项错误,
B.变形为x=2=4,即B项错误,
C.4x﹣8=0变形为(4x﹣8+8)=8×,即C项正确,
D.﹣=1变形为3(x﹣1)﹣2=6,即D项错误,
故选:C.
6.解:A、等式的两边都乘以2,得x=0,故A不符合题意;
B、左边加3,右边减3,故B不符合题意;
C、左边除以﹣3,右边乘以﹣3,故C不符合题意;
D、左边减去2,右边减去2,故D符合题意;
故选:D.
7.解:把x=0代入方程,得
1﹣=
解得k=3.
故选:C.
8.解:∵k=
=
=
=2+,
∴当2x﹣1=1或2x﹣1=﹣1或2x﹣1=5或2x﹣1=﹣5时,k为整数,
解得:x=1或x=0或x=3或x=﹣2,
则满足k为整数的所有整数x的和为1+0+3﹣2=2,
故选:D.
9.解:设原计划每小时生产x个零件,则实际每小时生产(x+10)个零件.
根据等量关系列方程得:12(x+10)=13x+60.
故选:B.
10.解:设合伙人数为x人,
依题意,得:5x+45=7x+3.
故选:B.
二.填空题(共6小题)
11.解:由mx﹣1=2(x+),得
x=,
因为关于x的方程mx﹣1=2(x+)的解是正整数,得
m﹣2=1,m﹣2=2,或m﹣2=4.
解得m=3,m=4,或m=6.
故答案为:3或4或6.
12.解:由题意可知:|m+4|=1,
∴m=﹣3或﹣5,
∵m+3≠0,
∴m≠﹣3,
∴m=﹣5,
故答案为:﹣5
13.解:令y1=|x|,y2=ax+2,
观察图象可知,要使方程有且仅有一个负数根,a≥1,
故答案为:a≥1.
14.解:2(x﹣2)=20﹣5(x+3),
2x﹣4=20﹣5x﹣15,
7x=9,
解得:x=.
把x=代入方程|3x﹣2|=b得:|3×﹣2|=b,
解得:b=.
故答案为:.
15.解:由题意,得船离A码头为:5(m+n)﹣5(m﹣n)=10n.
故答案是:10n.
16.解:若x=1,根据题意得:2x+4=2+4=6,
将x=6输入得:2x+4=16,符合题意;
根据题意得:2x+4=16,
移项合并得:2x=12,
解得:x=6,
综上,x的值为1或6.
故答案为:1或6.
17.解:(1)移项得:﹣3x=9+6,
合并同类项得:﹣3x=15,
系数化为1得:x=﹣5,
(2)移项得:﹣4x+6x=7﹣5,
合并同类项得:2x=2,
系数化为1得:x=1,
(3)去括号得:2x﹣2+2=4x﹣6,
移项得:2x﹣4x=﹣6﹣2+2,
合并同类项得:﹣2x=﹣6,
系数化为1得:x=3,
(4)去分母得:3(x﹣2)﹣2(2﹣3x)=6,
去括号得:3x﹣6﹣4+6x=6,
移项得:3x+6x=6+6+4,
合并同类项得:9x=16,
系数化为1得:x=.
18.解:(1)移项,可得:12x﹣10x=7+5,
合并同类项,可得:2x=12,
解得:x=6.
(2)去分母得:12﹣12+9x=10x+6﹣12x,
移项,合并同类项,可得:11x=6,
解得:x=.
19.解:如图:
关于x的方程|x﹣2|+|x+1|=a的解可以看成是函数y=|x﹣2|+|x+1|与函数y=a的交点的横坐标,
则由方程有四个整数解可得函数y=a的图象必与直线y=3重合,
即当a=3时满足题意,
所以a的取值范围为a=3.
20.解:(1)解第一个方程4x+2m=3x+1,得x=1﹣2m,
解第二个方程3x+2m=6x+1,得x=,
1﹣2m=
解得m=;
(2)当m=时,(﹣2m)3﹣(m﹣)4=(﹣2×)3﹣(﹣)4=﹣2.
21.解:设安排x人生产大齿轮,根据题意可得:,
解得:x=25
答:25人生产大齿轮.
22.解:(1)∵点A所对应的数a满足|a+1|=0,
∴a=﹣4.
∵AB=12,且点B在原点O的右侧,
∴点B表示的数为8.
故答案为:﹣4;8.
(2)当运动时间为t秒时(0≤t≤4),点D表示的数为t﹣4,点E表示的数为8﹣2t,
∴点P表示的数为t﹣4+=2﹣t,
∴d=﹣t+2(0≤t≤4).
(3)∵点C在线段AB上,且AC=2BC,
∴点C表示的数为4,
∴CE=|8﹣2t﹣4|=|4﹣2t|,CD=4﹣(t﹣4)=8﹣t.
∵2OP+3CE=CD,即2×(﹣t+2)+3×|4﹣2t|=8﹣t,
∴t=或,
∴当t为秒或秒时,2OP+3CE=CD.
23.解:方案一:最多生产4吨奶片,其余的鲜奶直接销售,
则其利润为:4×2000+(8﹣4)×500=10000(元);
方案二:设生产x天奶片,则生产(4﹣x)天酸奶,
根据题意得:x+3(4﹣x)=8,
解得:x=2,
2天生产酸奶加工的鲜奶是2×3=6吨,
则利润为:2×2000+2×3×1200=4000+7200=11200(元),
得到第二种方案可以多得1200元的利润.
24.解:(1)a=60÷100=0.6(元/度),
居民乙用电200度,则应交电费:150×0.6+50×0.65=122.5(元),
故答案是:0.6;122.5;
(2)用电超过300度时.设该户居民月用电x度时,则应交的电费=0.6×150+0.65×150+0.9(x﹣300)=0.9x﹣147.5,
(3)设该户居民月用电y千瓦时,分三种情况:
①若y不超过150,平均电价为0.6<0.62,故不合题意;
②若y超过150,但不超过300,则0.62y=0.6×150+0.65(y﹣150),
解得y=250;
③若y大于300,则0.62y=0.6×150+0.65×150+0.9(y﹣300),
解得y=294.
此时y<300,不合题意,应舍去.
综上所述,y=250.
答:该户居民月用电250度.
25.解:探究:(1)由题意,得
y1=200t,y2=﹣200t+1600
当相遇前相距400米时,
﹣200t+1600﹣200t=400,
t=3,
当相遇后相距400米时,
200t﹣(﹣200t+1600)=400,
t=5.
答:当两车相距的路程是400米时t的值为3分钟或5分钟;
(2)由题意,得
1号车第三次恰好经过景点C行驶的路程为:800×2+800×4×2=8000,
∴1号车第三次经过景点C需要的时间为:8000÷200=40分钟,
两车第一次相遇的时间为:1600÷400=4.
第一次相遇后两车每相遇一次需要的时间为:800×4÷400=8,
∴两车相遇的次数为:(40﹣4)÷8+1=5次.
∴这一段时间内它与2号车相遇的次数为:5次;
发现:由题意,得
情况一需要时间为:=16﹣,
情况二需要的时间为:=16+
∵16﹣<16+
∴情况二用时较多.
决策:(1)∵游客乙在AD边上与2号车相遇,
∴此时1号车在CD边上,
∴乘1号车到达A的路程小于2个边长,乘2号车的路程大于3个边长,
∴乘1号车的用时比2号车少.
(2)若步行比乘1号车的用时少,
,
∴s<320.
∴当0<s<320时,选择步行.
同理可得
当320<s<800时,选择乘1号车,
当s=320时,选择步行或乘1号车一样.
1.在①2x+1;②1+7=15﹣8+1;③;④x+2y=3中,方程共有( )
A.1个 B.2个 C.3个 D.4个
2.下列所给条件,不能列出方程的是( )
A.某数比它的平方小6
B.某数加上3,再乘以2等于14
C.某数与它的的差
D.某数的3倍与7的和等于29
3.下列各判断句中,错误的是( )
A.方程是等式,但等式不一定是方程
B.由ax=ay这个条件不能得到x=y一定成立的结论
C.在整数范围内,方程6x=3无解
D.x5=0不是方程
4.若x=1是ax+2x=3方程的解,则a的值是( )
A.﹣1 B.1 C.﹣3 D.3
5.下列方程变形正确的是( )
A.2x﹣5=5x+4变形为2x﹣5=5x+4﹣5x﹣4
B.x=2变形为x=2×=1
C.4x﹣8=0变形为(4x﹣8+8)=8×
D.﹣=1变形为3(x﹣1)﹣2=1
6.下列方程的变形,符合等式性质的是( )
A.由x=0,得x=2 B.由x﹣3=5,得x=5﹣3
C.﹣3x=,得x=﹣ D.由x+2=4,得x=4﹣2
7.若x=0是方程的解,则k值为( )
A.0 B.2 C.3 D.4
8.已知k=,则满足k为整数的所有整数x的和是( )
A.﹣1 B.0 C.1 D.2
9.某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,设原计划每小时生产x个零件,则所列方程为( )
A.13x=12(x+10)+60 B.12(x+10)=13x+60
C. D.
10.《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为x人,所列方程正确的是( )
A.5x﹣45=7x﹣3 B.5x+45=7x+3 C.= D.=
11.已知关于x的一元一次方程mx﹣1=2(x+)的解是正整数,则整数m的值为 .
12.已知关于x的方程(m+3)x|m+4|+18=0是一元一次方程,则m的值为 .
13.方程|x|=ax+2有且仅有一个负数根,则a的取值范围是 .
14.已知方程的解也是方程|3x﹣2|=b的解,则b= .
15.一艘船在水中航行,已知该船在静水中的速度为m(千米/小时),水流速度为n(千米/小时),如果该船从码头A出发,先顺流航行5小时,然后又调头逆流航行了5小时,那么最后船离A码头 千米.
16.小颖按如图所示的程序输入一个正数x,最后从输出端得到的数为16,求小颖输入的数x的值 .
17.解下列方程:
(1)﹣3x﹣6=9 (2)5﹣4x=﹣6x+7
(3)2(x﹣1)+2=4x﹣6 (4)=1.
18.解下列方程
(1)10x+7=12x﹣5 (2)1﹣=.
19.若关于x的方程|x﹣2|+|x+1|=a有四个整数解,求a的取值范围.
20.已知关于x的方程4x+2m=3x+1与方程3x+2m=6x+1的解相同;
(1)求m的值;
(2)求代数式(﹣2m)3﹣(m﹣)4的值.
21.某车间有工人85人,平均每人每天可加工大齿轮16个或小齿轮10个,又知2个大齿轮和3个小齿轮配套,问应安排多少个工人生产大齿轮使生产的产品刚好成套?
22.如图,在数轴上,点A在原点O的左侧,点B在原点O的右侧,点A所对应的数a满足|a+1|=0,且AB=12,点D从A出发以1个单位长度/秒的速度沿数轴向右运动,点E从B出发以2个单位长度/秒的速度沿数轴向左运动,当D、E两点相遇时停止运动.
(1)直接写出点A表示的数为 ,点B表示的数为 ;
(2)点P为线段DE的中点,D、E两点同时开始运动,设运动时间为t秒,线段OP的长为d个单位长度,求用含t的整式表示d;
(3)在(2)条件下,点C在线段AB上,且AC=2BC,当t为何值时,满足2OP+3CE=CD.
23.某牛奶加工厂现有鲜奶8吨,若市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润2000元.该工厂的生产能力是:如制成酸奶每天可加工3吨;制成奶片每天可加工1吨.受人员制约,两种加工方式不可同时进行;受气温制约,这批牛奶必须在4天内全部销售或加工完毕.为此,该工厂设计了两种可行方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多?为什么?
24.据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见表:若2015年5月份,该市居民甲用电100度,交电费60元.
一户居民一个月用电量的范围 电费价格(单位:元/度)
不超过150度 a
超过150度但不超过300度的部分 0.65
超过300度的部分 0.9
(1)表中,a= ;若居民乙用电200度,则应交电费 元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度0.62元?
25.某景区内的环形路是边长为800米的正方形ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
探究:设行驶时间为t分.
(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y1,y2(米)与t(分)的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇过的次数.
发现:如图2,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多?(含候车时间)
决策:已知游客乙在DA上从D向出口A走去.步行的速度是50米/分.当行进到DA上一点P(不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由:
(2)设PA=s(0<s<800)米.若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中.他该如何选择?
参考答案
1.解:(1)2x+1,含未知数但不是等式,所以不是方程.
(2)1+7=15﹣8+1,是等式但不含未知数,所以不是方程.
(3),是含有未知数的等式,所以是方程.
(4)x+2y=3,是含有未知数的等式,所以是方程.
故有所有式子中有2个是方程.
故选:B.
2.解:设某数为x,
A、x2﹣x=6,是方程,故本选项错误;
B、2(x+3)=14,是方程,故本选项错误;
C、x﹣x,不是方程,故本选项正确;
D、3x+7=29,是方程,故本选项错误.
故选:C.
3.解:A、方程是含有未知数的等式,而等式中不一定含有未知数,所以“方程是等式,但等式不一定是方程”这种说法正确.故本选项不符合题意;
B、当a=0时,等式ax=ay恒成立,但是x不一定与y相等,所以“由ax=ay这个条件不能得到x=y一定成立的结论”这种说法正确.故本选项不符合题意;
C、方程6x=3的解是x=,不是整数,所以“在整数范围内,方程6x=3无解”这种说法正确.故本选项不符合题意;
D、x5=0是含有未知数的等式,所以它是方程.故本选项符合题意.
故选:D.
4.解:根据题意,将x=1代入方程ax+2x=3,
得:a+2=3,
得:a=1.
故选:B.
5.解:A.2x﹣5=5x+4变形为2x﹣5﹣5x﹣4=5x+4﹣5x﹣4,即A项错误,
B.变形为x=2=4,即B项错误,
C.4x﹣8=0变形为(4x﹣8+8)=8×,即C项正确,
D.﹣=1变形为3(x﹣1)﹣2=6,即D项错误,
故选:C.
6.解:A、等式的两边都乘以2,得x=0,故A不符合题意;
B、左边加3,右边减3,故B不符合题意;
C、左边除以﹣3,右边乘以﹣3,故C不符合题意;
D、左边减去2,右边减去2,故D符合题意;
故选:D.
7.解:把x=0代入方程,得
1﹣=
解得k=3.
故选:C.
8.解:∵k=
=
=
=2+,
∴当2x﹣1=1或2x﹣1=﹣1或2x﹣1=5或2x﹣1=﹣5时,k为整数,
解得:x=1或x=0或x=3或x=﹣2,
则满足k为整数的所有整数x的和为1+0+3﹣2=2,
故选:D.
9.解:设原计划每小时生产x个零件,则实际每小时生产(x+10)个零件.
根据等量关系列方程得:12(x+10)=13x+60.
故选:B.
10.解:设合伙人数为x人,
依题意,得:5x+45=7x+3.
故选:B.
二.填空题(共6小题)
11.解:由mx﹣1=2(x+),得
x=,
因为关于x的方程mx﹣1=2(x+)的解是正整数,得
m﹣2=1,m﹣2=2,或m﹣2=4.
解得m=3,m=4,或m=6.
故答案为:3或4或6.
12.解:由题意可知:|m+4|=1,
∴m=﹣3或﹣5,
∵m+3≠0,
∴m≠﹣3,
∴m=﹣5,
故答案为:﹣5
13.解:令y1=|x|,y2=ax+2,
观察图象可知,要使方程有且仅有一个负数根,a≥1,
故答案为:a≥1.
14.解:2(x﹣2)=20﹣5(x+3),
2x﹣4=20﹣5x﹣15,
7x=9,
解得:x=.
把x=代入方程|3x﹣2|=b得:|3×﹣2|=b,
解得:b=.
故答案为:.
15.解:由题意,得船离A码头为:5(m+n)﹣5(m﹣n)=10n.
故答案是:10n.
16.解:若x=1,根据题意得:2x+4=2+4=6,
将x=6输入得:2x+4=16,符合题意;
根据题意得:2x+4=16,
移项合并得:2x=12,
解得:x=6,
综上,x的值为1或6.
故答案为:1或6.
17.解:(1)移项得:﹣3x=9+6,
合并同类项得:﹣3x=15,
系数化为1得:x=﹣5,
(2)移项得:﹣4x+6x=7﹣5,
合并同类项得:2x=2,
系数化为1得:x=1,
(3)去括号得:2x﹣2+2=4x﹣6,
移项得:2x﹣4x=﹣6﹣2+2,
合并同类项得:﹣2x=﹣6,
系数化为1得:x=3,
(4)去分母得:3(x﹣2)﹣2(2﹣3x)=6,
去括号得:3x﹣6﹣4+6x=6,
移项得:3x+6x=6+6+4,
合并同类项得:9x=16,
系数化为1得:x=.
18.解:(1)移项,可得:12x﹣10x=7+5,
合并同类项,可得:2x=12,
解得:x=6.
(2)去分母得:12﹣12+9x=10x+6﹣12x,
移项,合并同类项,可得:11x=6,
解得:x=.
19.解:如图:
关于x的方程|x﹣2|+|x+1|=a的解可以看成是函数y=|x﹣2|+|x+1|与函数y=a的交点的横坐标,
则由方程有四个整数解可得函数y=a的图象必与直线y=3重合,
即当a=3时满足题意,
所以a的取值范围为a=3.
20.解:(1)解第一个方程4x+2m=3x+1,得x=1﹣2m,
解第二个方程3x+2m=6x+1,得x=,
1﹣2m=
解得m=;
(2)当m=时,(﹣2m)3﹣(m﹣)4=(﹣2×)3﹣(﹣)4=﹣2.
21.解:设安排x人生产大齿轮,根据题意可得:,
解得:x=25
答:25人生产大齿轮.
22.解:(1)∵点A所对应的数a满足|a+1|=0,
∴a=﹣4.
∵AB=12,且点B在原点O的右侧,
∴点B表示的数为8.
故答案为:﹣4;8.
(2)当运动时间为t秒时(0≤t≤4),点D表示的数为t﹣4,点E表示的数为8﹣2t,
∴点P表示的数为t﹣4+=2﹣t,
∴d=﹣t+2(0≤t≤4).
(3)∵点C在线段AB上,且AC=2BC,
∴点C表示的数为4,
∴CE=|8﹣2t﹣4|=|4﹣2t|,CD=4﹣(t﹣4)=8﹣t.
∵2OP+3CE=CD,即2×(﹣t+2)+3×|4﹣2t|=8﹣t,
∴t=或,
∴当t为秒或秒时,2OP+3CE=CD.
23.解:方案一:最多生产4吨奶片,其余的鲜奶直接销售,
则其利润为:4×2000+(8﹣4)×500=10000(元);
方案二:设生产x天奶片,则生产(4﹣x)天酸奶,
根据题意得:x+3(4﹣x)=8,
解得:x=2,
2天生产酸奶加工的鲜奶是2×3=6吨,
则利润为:2×2000+2×3×1200=4000+7200=11200(元),
得到第二种方案可以多得1200元的利润.
24.解:(1)a=60÷100=0.6(元/度),
居民乙用电200度,则应交电费:150×0.6+50×0.65=122.5(元),
故答案是:0.6;122.5;
(2)用电超过300度时.设该户居民月用电x度时,则应交的电费=0.6×150+0.65×150+0.9(x﹣300)=0.9x﹣147.5,
(3)设该户居民月用电y千瓦时,分三种情况:
①若y不超过150,平均电价为0.6<0.62,故不合题意;
②若y超过150,但不超过300,则0.62y=0.6×150+0.65(y﹣150),
解得y=250;
③若y大于300,则0.62y=0.6×150+0.65×150+0.9(y﹣300),
解得y=294.
此时y<300,不合题意,应舍去.
综上所述,y=250.
答:该户居民月用电250度.
25.解:探究:(1)由题意,得
y1=200t,y2=﹣200t+1600
当相遇前相距400米时,
﹣200t+1600﹣200t=400,
t=3,
当相遇后相距400米时,
200t﹣(﹣200t+1600)=400,
t=5.
答:当两车相距的路程是400米时t的值为3分钟或5分钟;
(2)由题意,得
1号车第三次恰好经过景点C行驶的路程为:800×2+800×4×2=8000,
∴1号车第三次经过景点C需要的时间为:8000÷200=40分钟,
两车第一次相遇的时间为:1600÷400=4.
第一次相遇后两车每相遇一次需要的时间为:800×4÷400=8,
∴两车相遇的次数为:(40﹣4)÷8+1=5次.
∴这一段时间内它与2号车相遇的次数为:5次;
发现:由题意,得
情况一需要时间为:=16﹣,
情况二需要的时间为:=16+
∵16﹣<16+
∴情况二用时较多.
决策:(1)∵游客乙在AD边上与2号车相遇,
∴此时1号车在CD边上,
∴乘1号车到达A的路程小于2个边长,乘2号车的路程大于3个边长,
∴乘1号车的用时比2号车少.
(2)若步行比乘1号车的用时少,
,
∴s<320.
∴当0<s<320时,选择步行.
同理可得
当320<s<800时,选择乘1号车,
当s=320时,选择步行或乘1号车一样.
