2021--2022学年沪科版九年级数学上册第22章 相似形 单元自测卷 (Word版含答案)
文档属性
| 名称 | 2021--2022学年沪科版九年级数学上册第22章 相似形 单元自测卷 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 430.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:55:02 | ||
图片预览



文档简介
沪科版九年级数学上册第22章相似形单元自测卷
班级 姓名 学号
一、单选题(40分)
1.根据下列各组条件,不能判定△ABC∽△A1B1C1的是( )
A.∠B=∠B1=60°,∠C=50°,∠A1=70°
B.∠C=∠C1=90°,AB=10,AC=6,A1B1=5,A1C1=3
C.∠A=40°,AB=2,AC=3,∠A1=40°,A1B1=4,A1C1=5
D.AB=12,BC=15,AC=24,A1B1=8,A1C1=16,B1C1=10
2.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′:,则四边形ABCD与四边形A′B′C′D′的面积比为( )
A.4:9 B.2:5 C.2:3 D.5:5
3.如图,在中,,点在边上,,E为边上一点,当时,的值为
A. B. C. D.
(3) (4)(5)
4.如图,有一块形状为Rt△ABC的斜板余料,∠A=90°,AB=6cm,AC=8cm,要把它加工成一个形状为 DEFG的工件,使GF在边BC上,D、E两点分别在边AB、AC上,若点D是边AB的中点,则S DEFG的面积为( )cm2.
A.10 B.12 C.14 D.16
5.如图,在平面直角坐标系中,点A在函数 的图象上,点B在函数的图象上,若AO=2BO,∠AOB=90°,则k的值为( )
A.1 B.2 C.1.5 D.0.25
6.如图,中,点E、F在BC边上,点D、G分别在AB、AC边上,四边形DEFG是矩形.若矩形DEFG的面积与的面积相等,设的BC边上高AH与DG相交于点K,则的值为( )
A. B. C. D.
(6)(7)(8)
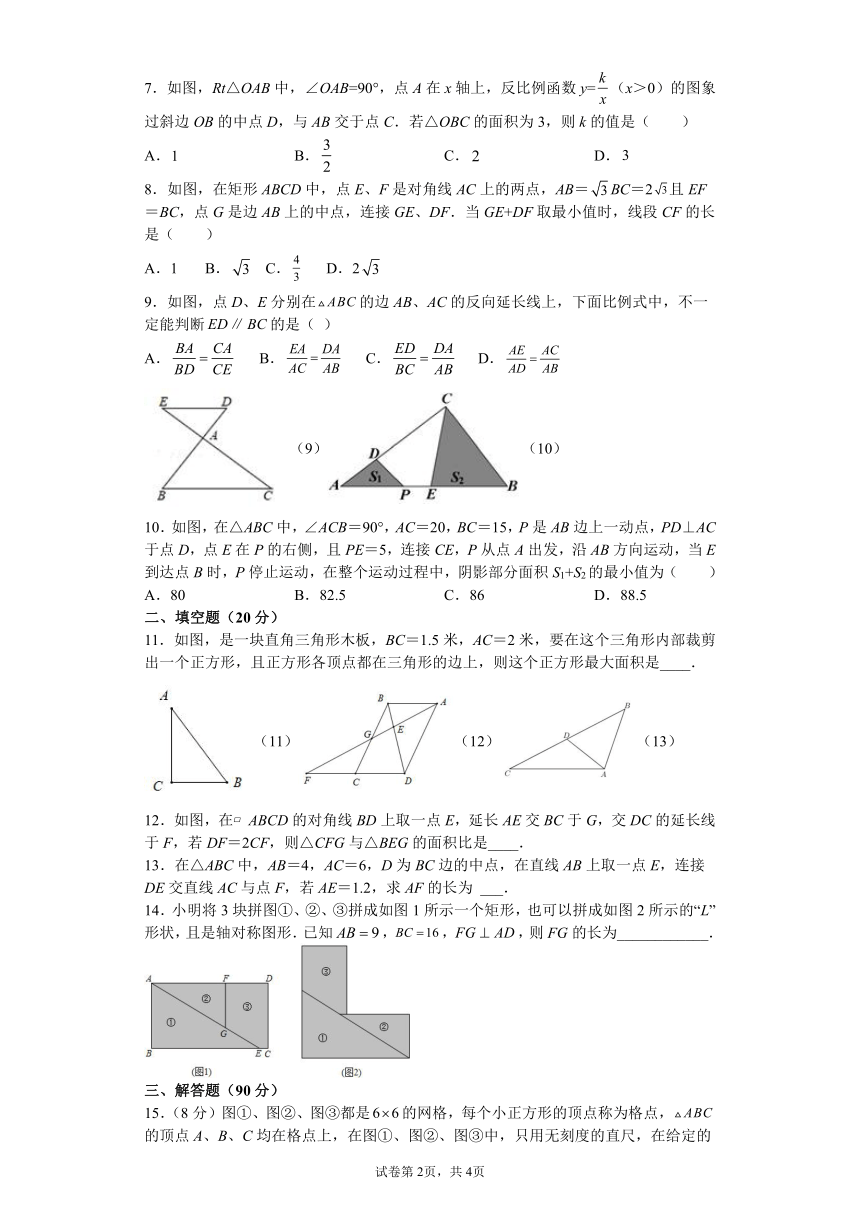
7.如图,Rt△OAB中,∠OAB=90°,点A在x轴上,反比例函数y=(x>0)的图象过斜边OB的中点D,与AB交于点C.若△OBC的面积为3,则k的值是( )
A. B. C. D.
8.如图,在矩形ABCD中,点E、F是对角线AC上的两点,AB=BC=2且EF=BC,点G是边AB上的中点,连接GE、DF.当GE+DF取最小值时,线段CF的长是( )
A.1 B. C. D.2
9.如图,点D、E分别在的边AB、AC的反向延长线上,下面比例式中,不一定能判断的是( )
A. B. C. D.
(9)(10)
10.如图,在△ABC中,∠ACB=90°,AC=20,BC=15,P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=5,连接CE,P从点A出发,沿AB方向运动,当E到达点B时,P停止运动,在整个运动过程中,阴影部分面积S1+S2的最小值为( )
A.80 B.82.5 C.86 D.88.5
二、填空题(20分)
11.如图,是一块直角三角形木板,BC=1.5米,AC=2米,要在这个三角形内部裁剪出一个正方形,且正方形各顶点都在三角形的边上,则这个正方形最大面积是____.
(11)(12)(13)
12.如图,在 ABCD的对角线BD上取一点E,延长AE交BC于G,交DC的延长线于F,若DF=2CF,则△CFG与△BEG的面积比是____.
13.在△ABC中,AB=4,AC=6,D为BC边的中点,在直线AB上取一点E,连接DE交直线AC与点F,若AE=1.2,求AF的长为 ___.
14.小明将3块拼图①、②、③拼成如图1所示一个矩形,也可以拼成如图2所示的“L”形状,且是轴对称图形.已知,,,则FG的长为____________.
三、解答题(90分)
15.(8分)图①、图②、图③都是的网格,每个小正方形的顶点称为格点,的顶点A、B、C均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求作图.不要求写出画法.
(1)在图①中画出边BC上的中线AD,则_______;
(2)在图②中画出,点E、F分别在边AB、BC上,满足,且;
16.(8分)如图,△ABC中,∠A=90°,BC=13cm,AC=12cm,点E从C出发,在边CA上以2cm/s的速度移动,点D从A出发、在边AB上以1cm/s的速度移动、若E,D分别同时从C,A出发,当一个点到达终点时,另一个点也停止移动.经过多少时间以A,D,E为顶点的三角形与以C,B,A为顶点的三角形相似?
17.(8分)如图,在中,,于,作于,是中点,连结交于点.
(1)求证:;
(2)若,,求的值.
18.(8分)如图,在矩形ABCD中,AB=3,BC=4,动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向终点A运动,P,Q运动速度均为每秒1个单位长度,当一个点到达终点时,另一个点也停止运动,连接PQ,设运动时间为t(t>0)秒.
(1)t为何值时,△AQP与△ABC相似?
(2)t为何值时,△AQP的面积为0.8?
19.(10分)如图,在矩形ABCD中,沿直线MN对折,使A、C重合,直线MN交AC于O.
求证:
20.(10分)如图,在ABC中,AB=AC,∠A为锐角且不等于60°,AD平分∠BAC交BC于点D,BE⊥AC于点E,AD交BE于点F.
(1)写出图中所有与ACD相似的三角形(全等除外);
(2)连接DE,求证:ABF∽△EDF.
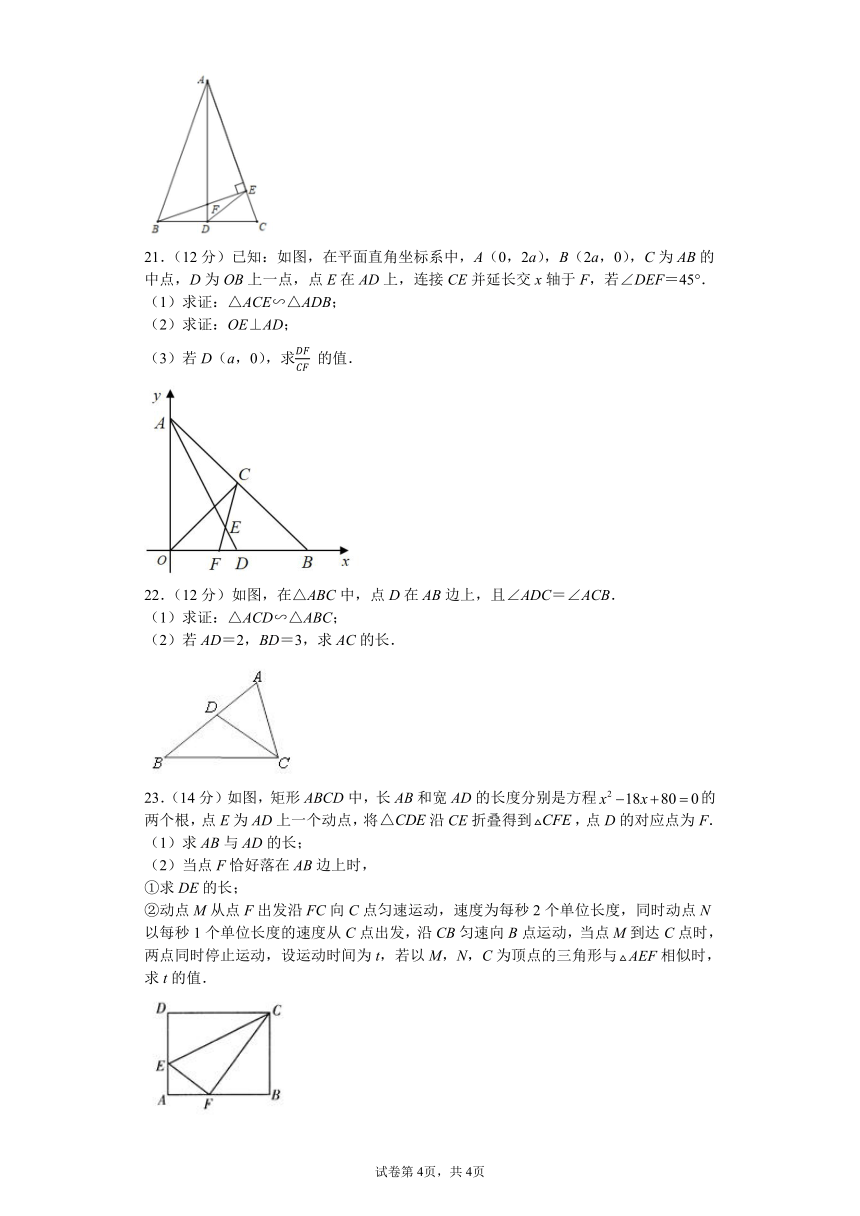
21.(12分)已知:如图,在平面直角坐标系中,A(0,2a),B(2a,0),C为AB的中点,D为OB上一点,点E在AD上,连接CE并延长交x轴于F,若∠DEF=45°.
(1)求证:△ACE∽△ADB;
(2)求证:OE⊥AD;
(3)若D(a,0),求 的值.
22.(12分)如图,在△ABC中,点D在AB边上,且∠ADC=∠ACB.
(1)求证:△ACD∽△ABC;
(2)若AD=2,BD=3,求AC的长.
23.(14分)如图,矩形ABCD中,长AB和宽AD的长度分别是方程的两个根,点E为AD上一个动点,将沿CE折叠得到,点D的对应点为F.
(1)求AB与AD的长;
(2)当点F恰好落在AB边上时,
①求DE的长;
②动点M从点F出发沿FC向C点匀速运动,速度为每秒2个单位长度,同时动点N以每秒1个单位长度的速度从C点出发,沿CB匀速向B点运动,当点M到达C点时,两点同时停止运动,设运动时间为t,若以M,N,C为顶点的三角形与相似时,求t的值.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C2.B3.A4.B5.A6.C7.C8.C9.C10.B
11.12.13.或14.6
15.(1)作图见解析部分,6;(2)作图见解析部分.
【详解】
解:(1)如图①中,
线段即为所求.,
故答案为6.
(2)如图②中,
线段即为所求.
16.经过秒或秒时,以A,D,E为顶点的三角形与以C,B,A为顶点的三角形相似.
【详解】
解:∵△ABC中,∠A=90°,BC=13cm,AC=12cm,
∴AB=5,
∵点D以每秒1个单位长度的速度由A向B运动,同时点E以每秒2个单位长度的速度由C向A运动,
∴AD=t,AE=12-2t,
∴当△ADE∽△ABC时,,即,解得t=(秒);
当△AED∽△ABC时,,即,解得t=(秒);
综上所述,经过秒或秒时,以A,D,E为顶点的三角形与以C,B,A为顶点的三角形相似.
17.(1)证明见解析;(2).
【详解】
解:(1)∵,,
∴.
由题意可知,
∴,
∴,
∴.
(2)如图,连接FD.
∵,,
∴D点为BC中点,
∴DF为中位线.
∴,且,
∴,即,
∴.
18.(1)当或时,△ABC与△AQP相似;(2)当或2时,△AQP的面积为0.8.
【详解】
解:(1)由题意得:,
∵AB=3,BC=4,
∴AC=5,
由可知,△ABC与△AQP相似时,存在以下两种情况:
①当△ABC∽△AQP时,则有:
,即,
解得:;
②当△ABC∽△APQ时,则有:
,即,
解得:;
综上所述:当或时,△ABC与△AQP相似;
(2)过点P作PE⊥AB于点E,如图所示:
∴PE∥BC,
∴△ABC∽△AEP,
∴,即,
∴,
∴,
整理得:,
解得:,
∴当或2时,△AQP的面积为0.8.
19.见解析
【详解】
证明:∵沿直线对折,使A、C重合,
∴A与C关于直线对称,
∴,
∴
在矩形中,
∴,
又∵,
∴,
∴
∴.
20.(1)△AFE、△BCE、△BFD;(2)见解析
【分析】
(1)由等腰三角形的性质得出AD⊥BC,由两角相等证得与ACD相似的三角形有△AFE、△BCE、△BFD;
(2)由两角相等证得△AFE∽△BFD,得出即,有由夹角相等,即可证得结论.
【详解】
解(1)与△ACD相似的三角形有:△AFE、△BCE、△BFD证明如下:
∵AD平分∠BAC,AB=AC,
∴AD⊥BC,
由∵BE⊥AC,
∴∠ADC=∠ADB=∠AEC=∠AEB=90°,
又∵∠EAF=∠DAC,
∴△AFE∽△ACD;
又∵∠C=∠C,
∴△BCE∽△ACD,
∴∠DBE=∠DAC,
又∵∠BDF=∠ADC=90°,
∴△BFD∽△ACD;
(2)∵△BFD∽△ACD,
∴∠CAD=∠CBE,
又∵∠AFE=∠BFD,
∴△AFE∽△BFD,
∴,
∴,
∵∠AFB=∠EFD,
∴ABF∽△EDF.
21.(1)见解析;(2)见解析;(3)
【详解】
解:(1)∵A(0,2a),B(2a,0),
∴OA=OB=2a,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵∠DEF=45°,
∴∠OBA=∠DEF,
∵∠DEF =∠AEC,
∴∠OBA=∠AEC,
∵∠CAE=∠BAE,
∴△ACE∽△ADB;
(2)由(1)知:△ACE∽△ADB,
∴ ,
∴ ,
∵C为AB的中点,
∴AB=2AC,
∴,
∵∠AOB=90°,AO=BO,C为AB的中点,
∴OC⊥AB,
∴∠AOC=∠OAC=45°,
∴ 是等腰直角三角形,
∴AC=OC,
∴ ,
∴ ,
∴ ,
∵∠OAE=∠DAO,
∴ ,
∴∠AEO=∠AOD=90°,
∴OE⊥AD;
(3)∵OE⊥AD,
∴∠AEO=∠OED=90°,
∵∠AOB=90°,
∴∠OED=∠AOB,
∵∠ODE=∠ODA,
∴△OED∽△AOD,
∴ ,
∵A(0,2a),B(2a,0),D(a,0),
∴OA=OB=2a,OD=a,
∴ ,
∴,解得: ,
∵∠B=∠DEF=45°,∠DFE=∠BFC,
∴△DEF∽△CBF,
∴ ,
∵OA=OB=2a,∠AOB=90°,
∴ ,
∵C为AB的中点,
∴ ,
∴.
22.(1)见解析;(2).
【详解】
解:(1)证明:如图,∵∠ADC=∠ACB,∠CAD=∠BAC,
∴△ACD∽△ABC;
(2)∵点D在AB边上,AD=2,BD=3,
∴AB=AD+BD=2+3=5,
∵△ACD∽△ABC,
∴,
∴,
∴.
23.(1),;(2)①;②当或时,以M、N、C为顶点的三角形与相似.
【详解】
解:(1)∵长AB和宽AD的长度分别是方程的两个根,
可得,,,
即,;
(2)①由折叠可得,,而,
∴,∴,
设,则,
中,,
∴,解得,∴;
②∵,,
∴,
由①可得,,,,
∵,,
∴,
①当时,,
∴,即,解得;
②当时,,
∴,即,解得,
综上所述,当或时,以M、N、C为顶点的三角形与相似.
答案第1页,共2页
答案第1页,共2页
班级 姓名 学号
一、单选题(40分)
1.根据下列各组条件,不能判定△ABC∽△A1B1C1的是( )
A.∠B=∠B1=60°,∠C=50°,∠A1=70°
B.∠C=∠C1=90°,AB=10,AC=6,A1B1=5,A1C1=3
C.∠A=40°,AB=2,AC=3,∠A1=40°,A1B1=4,A1C1=5
D.AB=12,BC=15,AC=24,A1B1=8,A1C1=16,B1C1=10
2.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′:,则四边形ABCD与四边形A′B′C′D′的面积比为( )
A.4:9 B.2:5 C.2:3 D.5:5
3.如图,在中,,点在边上,,E为边上一点,当时,的值为
A. B. C. D.
(3) (4)(5)
4.如图,有一块形状为Rt△ABC的斜板余料,∠A=90°,AB=6cm,AC=8cm,要把它加工成一个形状为 DEFG的工件,使GF在边BC上,D、E两点分别在边AB、AC上,若点D是边AB的中点,则S DEFG的面积为( )cm2.
A.10 B.12 C.14 D.16
5.如图,在平面直角坐标系中,点A在函数 的图象上,点B在函数的图象上,若AO=2BO,∠AOB=90°,则k的值为( )
A.1 B.2 C.1.5 D.0.25
6.如图,中,点E、F在BC边上,点D、G分别在AB、AC边上,四边形DEFG是矩形.若矩形DEFG的面积与的面积相等,设的BC边上高AH与DG相交于点K,则的值为( )
A. B. C. D.
(6)(7)(8)
7.如图,Rt△OAB中,∠OAB=90°,点A在x轴上,反比例函数y=(x>0)的图象过斜边OB的中点D,与AB交于点C.若△OBC的面积为3,则k的值是( )
A. B. C. D.
8.如图,在矩形ABCD中,点E、F是对角线AC上的两点,AB=BC=2且EF=BC,点G是边AB上的中点,连接GE、DF.当GE+DF取最小值时,线段CF的长是( )
A.1 B. C. D.2
9.如图,点D、E分别在的边AB、AC的反向延长线上,下面比例式中,不一定能判断的是( )
A. B. C. D.
(9)(10)
10.如图,在△ABC中,∠ACB=90°,AC=20,BC=15,P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=5,连接CE,P从点A出发,沿AB方向运动,当E到达点B时,P停止运动,在整个运动过程中,阴影部分面积S1+S2的最小值为( )
A.80 B.82.5 C.86 D.88.5
二、填空题(20分)
11.如图,是一块直角三角形木板,BC=1.5米,AC=2米,要在这个三角形内部裁剪出一个正方形,且正方形各顶点都在三角形的边上,则这个正方形最大面积是____.
(11)(12)(13)
12.如图,在 ABCD的对角线BD上取一点E,延长AE交BC于G,交DC的延长线于F,若DF=2CF,则△CFG与△BEG的面积比是____.
13.在△ABC中,AB=4,AC=6,D为BC边的中点,在直线AB上取一点E,连接DE交直线AC与点F,若AE=1.2,求AF的长为 ___.
14.小明将3块拼图①、②、③拼成如图1所示一个矩形,也可以拼成如图2所示的“L”形状,且是轴对称图形.已知,,,则FG的长为____________.
三、解答题(90分)
15.(8分)图①、图②、图③都是的网格,每个小正方形的顶点称为格点,的顶点A、B、C均在格点上,在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求作图.不要求写出画法.
(1)在图①中画出边BC上的中线AD,则_______;
(2)在图②中画出,点E、F分别在边AB、BC上,满足,且;
16.(8分)如图,△ABC中,∠A=90°,BC=13cm,AC=12cm,点E从C出发,在边CA上以2cm/s的速度移动,点D从A出发、在边AB上以1cm/s的速度移动、若E,D分别同时从C,A出发,当一个点到达终点时,另一个点也停止移动.经过多少时间以A,D,E为顶点的三角形与以C,B,A为顶点的三角形相似?
17.(8分)如图,在中,,于,作于,是中点,连结交于点.
(1)求证:;
(2)若,,求的值.
18.(8分)如图,在矩形ABCD中,AB=3,BC=4,动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向终点A运动,P,Q运动速度均为每秒1个单位长度,当一个点到达终点时,另一个点也停止运动,连接PQ,设运动时间为t(t>0)秒.
(1)t为何值时,△AQP与△ABC相似?
(2)t为何值时,△AQP的面积为0.8?
19.(10分)如图,在矩形ABCD中,沿直线MN对折,使A、C重合,直线MN交AC于O.
求证:
20.(10分)如图,在ABC中,AB=AC,∠A为锐角且不等于60°,AD平分∠BAC交BC于点D,BE⊥AC于点E,AD交BE于点F.
(1)写出图中所有与ACD相似的三角形(全等除外);
(2)连接DE,求证:ABF∽△EDF.
21.(12分)已知:如图,在平面直角坐标系中,A(0,2a),B(2a,0),C为AB的中点,D为OB上一点,点E在AD上,连接CE并延长交x轴于F,若∠DEF=45°.
(1)求证:△ACE∽△ADB;
(2)求证:OE⊥AD;
(3)若D(a,0),求 的值.
22.(12分)如图,在△ABC中,点D在AB边上,且∠ADC=∠ACB.
(1)求证:△ACD∽△ABC;
(2)若AD=2,BD=3,求AC的长.
23.(14分)如图,矩形ABCD中,长AB和宽AD的长度分别是方程的两个根,点E为AD上一个动点,将沿CE折叠得到,点D的对应点为F.
(1)求AB与AD的长;
(2)当点F恰好落在AB边上时,
①求DE的长;
②动点M从点F出发沿FC向C点匀速运动,速度为每秒2个单位长度,同时动点N以每秒1个单位长度的速度从C点出发,沿CB匀速向B点运动,当点M到达C点时,两点同时停止运动,设运动时间为t,若以M,N,C为顶点的三角形与相似时,求t的值.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C2.B3.A4.B5.A6.C7.C8.C9.C10.B
11.12.13.或14.6
15.(1)作图见解析部分,6;(2)作图见解析部分.
【详解】
解:(1)如图①中,
线段即为所求.,
故答案为6.
(2)如图②中,
线段即为所求.
16.经过秒或秒时,以A,D,E为顶点的三角形与以C,B,A为顶点的三角形相似.
【详解】
解:∵△ABC中,∠A=90°,BC=13cm,AC=12cm,
∴AB=5,
∵点D以每秒1个单位长度的速度由A向B运动,同时点E以每秒2个单位长度的速度由C向A运动,
∴AD=t,AE=12-2t,
∴当△ADE∽△ABC时,,即,解得t=(秒);
当△AED∽△ABC时,,即,解得t=(秒);
综上所述,经过秒或秒时,以A,D,E为顶点的三角形与以C,B,A为顶点的三角形相似.
17.(1)证明见解析;(2).
【详解】
解:(1)∵,,
∴.
由题意可知,
∴,
∴,
∴.
(2)如图,连接FD.
∵,,
∴D点为BC中点,
∴DF为中位线.
∴,且,
∴,即,
∴.
18.(1)当或时,△ABC与△AQP相似;(2)当或2时,△AQP的面积为0.8.
【详解】
解:(1)由题意得:,
∵AB=3,BC=4,
∴AC=5,
由可知,△ABC与△AQP相似时,存在以下两种情况:
①当△ABC∽△AQP时,则有:
,即,
解得:;
②当△ABC∽△APQ时,则有:
,即,
解得:;
综上所述:当或时,△ABC与△AQP相似;
(2)过点P作PE⊥AB于点E,如图所示:
∴PE∥BC,
∴△ABC∽△AEP,
∴,即,
∴,
∴,
整理得:,
解得:,
∴当或2时,△AQP的面积为0.8.
19.见解析
【详解】
证明:∵沿直线对折,使A、C重合,
∴A与C关于直线对称,
∴,
∴
在矩形中,
∴,
又∵,
∴,
∴
∴.
20.(1)△AFE、△BCE、△BFD;(2)见解析
【分析】
(1)由等腰三角形的性质得出AD⊥BC,由两角相等证得与ACD相似的三角形有△AFE、△BCE、△BFD;
(2)由两角相等证得△AFE∽△BFD,得出即,有由夹角相等,即可证得结论.
【详解】
解(1)与△ACD相似的三角形有:△AFE、△BCE、△BFD证明如下:
∵AD平分∠BAC,AB=AC,
∴AD⊥BC,
由∵BE⊥AC,
∴∠ADC=∠ADB=∠AEC=∠AEB=90°,
又∵∠EAF=∠DAC,
∴△AFE∽△ACD;
又∵∠C=∠C,
∴△BCE∽△ACD,
∴∠DBE=∠DAC,
又∵∠BDF=∠ADC=90°,
∴△BFD∽△ACD;
(2)∵△BFD∽△ACD,
∴∠CAD=∠CBE,
又∵∠AFE=∠BFD,
∴△AFE∽△BFD,
∴,
∴,
∵∠AFB=∠EFD,
∴ABF∽△EDF.
21.(1)见解析;(2)见解析;(3)
【详解】
解:(1)∵A(0,2a),B(2a,0),
∴OA=OB=2a,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵∠DEF=45°,
∴∠OBA=∠DEF,
∵∠DEF =∠AEC,
∴∠OBA=∠AEC,
∵∠CAE=∠BAE,
∴△ACE∽△ADB;
(2)由(1)知:△ACE∽△ADB,
∴ ,
∴ ,
∵C为AB的中点,
∴AB=2AC,
∴,
∵∠AOB=90°,AO=BO,C为AB的中点,
∴OC⊥AB,
∴∠AOC=∠OAC=45°,
∴ 是等腰直角三角形,
∴AC=OC,
∴ ,
∴ ,
∴ ,
∵∠OAE=∠DAO,
∴ ,
∴∠AEO=∠AOD=90°,
∴OE⊥AD;
(3)∵OE⊥AD,
∴∠AEO=∠OED=90°,
∵∠AOB=90°,
∴∠OED=∠AOB,
∵∠ODE=∠ODA,
∴△OED∽△AOD,
∴ ,
∵A(0,2a),B(2a,0),D(a,0),
∴OA=OB=2a,OD=a,
∴ ,
∴,解得: ,
∵∠B=∠DEF=45°,∠DFE=∠BFC,
∴△DEF∽△CBF,
∴ ,
∵OA=OB=2a,∠AOB=90°,
∴ ,
∵C为AB的中点,
∴ ,
∴.
22.(1)见解析;(2).
【详解】
解:(1)证明:如图,∵∠ADC=∠ACB,∠CAD=∠BAC,
∴△ACD∽△ABC;
(2)∵点D在AB边上,AD=2,BD=3,
∴AB=AD+BD=2+3=5,
∵△ACD∽△ABC,
∴,
∴,
∴.
23.(1),;(2)①;②当或时,以M、N、C为顶点的三角形与相似.
【详解】
解:(1)∵长AB和宽AD的长度分别是方程的两个根,
可得,,,
即,;
(2)①由折叠可得,,而,
∴,∴,
设,则,
中,,
∴,解得,∴;
②∵,,
∴,
由①可得,,,,
∵,,
∴,
①当时,,
∴,即,解得;
②当时,,
∴,即,解得,
综上所述,当或时,以M、N、C为顶点的三角形与相似.
答案第1页,共2页
答案第1页,共2页
