2021-2022学年沪科版九年级数学下册第二十四章直线与圆的位置关系 单元练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学下册第二十四章直线与圆的位置关系 单元练习题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 377.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览



文档简介
直线与圆的位置关系
一、选择题
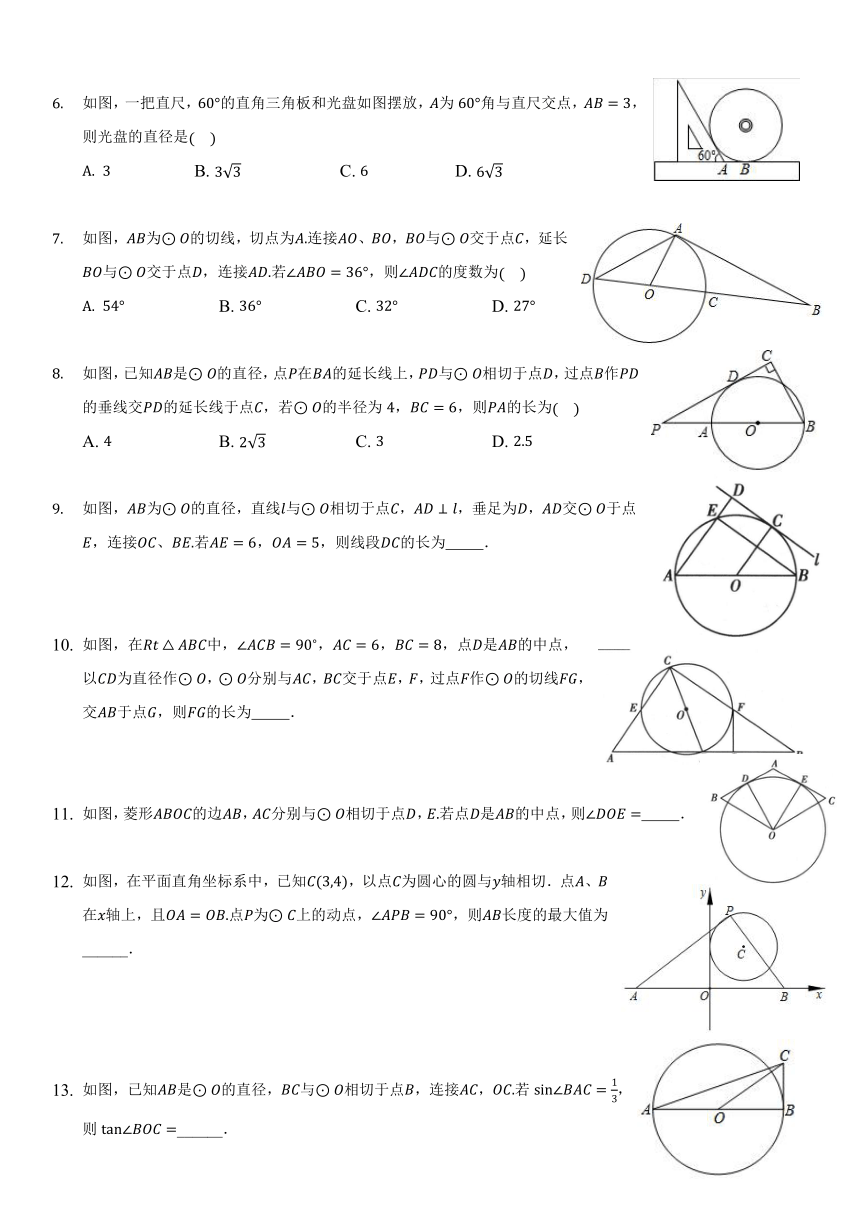
如图,是的直径,交于点,于点,要使是的切线,还需补充一个条件,则补充的条件不正确的是
A. B.
C. D.
如图,在中,是边上的点,以为圆心,为半径的与相切于点,平分,,,的长是
A. B. C. D.
如图,已知,是的两条切线,,为切点,线段交于点给出下列四种说法:
;
;
四边形有外接圆;
是外接圆的圆心.
其中正确说法的个数是
B. C. D.
如图,是的切线,点为切点,交于点,,点在上,则等于
B. C. D.
如图,为的直径,为的切线,弦,直线交的延长线于点,连接下列结论:是的切线;;∽;其中正确结论的个数有
个 B. 个 C. 个 D. 个
如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是
B. C. D.
如图,为的切线,切点为连接、,与交于点,延长与交于点,连接若,则的度数为
B. C. D.
如图,已知是的直径,点在的延长线上,与相切于点,过点作的垂线交的延长线于点,若的半径为,,则的长为
A. B. C. D.
如图,为的直径,直线与相切于点,,垂足为,交于点,连接、若,,则线段的长为 .
如图,在中,,,,点是的中点,以为直径作,分别与,交于点,,过点作的切线,交于点,则的长为 .
如图,菱形的边,分别与相切于点,若点是的中点,则 .
如图,在平面直角坐标系中,已知,以点为圆心的圆与轴相切.点、在轴上,且点为上的动点,,则长度的最大值为______.
如图,已知是的直径,与相切于点,连接,若,则______.
如图,是的弦,点在过点的切线上,且,交于点,已知,则______.
如图,已知是的直径,是的切线,连接交于点,连接若,则的度数是______
如图,是半圆的直径,,是半圆上不同于,的两点,,与相交于点是半圆所在圆的切线,与的延长线相交于点.
求证:≌;
若,求证:平分.
在中,为直径,为上一点.
如图,过点作的切线,与的延长线相交于点,若,求的大小
如图,为上一点,且经过的中点,连接并延长,与的延长线相交于点,若,求的大小.
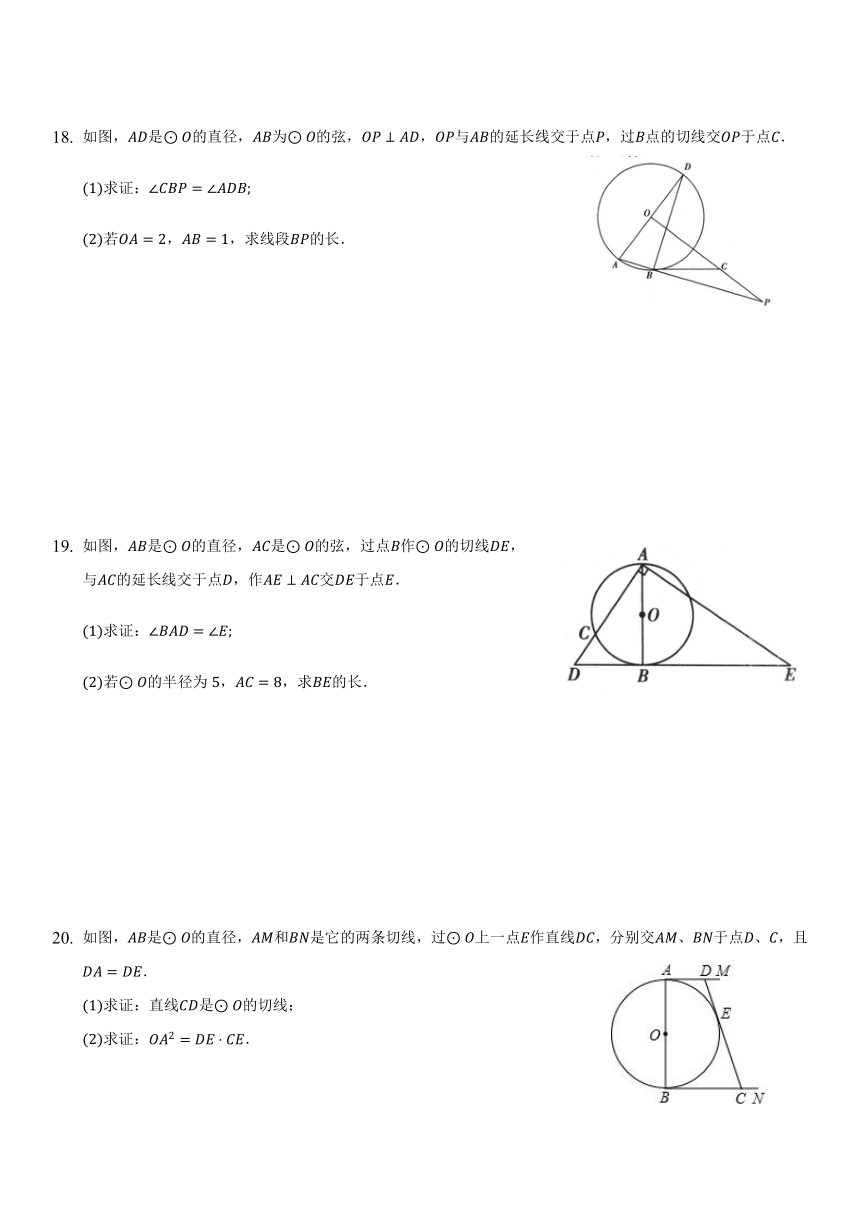
如图,是的直径,为的弦,,与的延长线交于点,过点的切线交于点.
求证:
若,,求线段的长.
如图,是的直径,是的弦,过点作的切线,与的延长线交于点,作交于点.
求证:
若的半径为,,求的长.
如图,是的直径,和是它的两条切线,过上一点作直线,分别交、于点、,且.
求证:直线是的切线;
求证:.
已知:如图,是的直径,点为上一点,点是上一点,连接并延长至点,使,与交于点.
求证:是的切线;
若平分,求证:.
如图,为的直径,为上一点,和过点的切线互相垂直,垂足为,且交于点连接,,相交于点.
求证:;
若,,求直径的长.
如图,已知是的直径,经过的直角边上的点,交边于点,点是弧的中点,,连接.
求证:直线是切线.
若,,求的值.
如图,在中,,点在上,以为半径的半圆交于点,交于点,过点作半圆的切线,交于点.
求证:;
若,,,求半圆的半径长.
如图,是的外接圆,点在边上,的平分线交于点,连接、,过点作的平行线,与的延长线相交于点.
求证:是的切线;
求证:∽;
当,时,求线段的长.
如图,为的直径,为延长线上一点,是的切线,为切点,于点,交于点.
求证:;
若,,求的长.
已知,分别与相切于点,,,为上一点.
Ⅰ如图,求的大小;
Ⅱ如图,为的直径,与相交于点若,求的大小.
如图,是的直径,点在的延长线上,、是上的两点,,,延长交的延长线于点.
求证:是的切线;
求证:;
若,,求弦的长.
如图,点在以为直径的上,平分交于点,过作的垂线,垂足为.
求证:与相切;
若,,求的长;
请用线段、表示的长,并说明理由
如图,为的直径,点在上,与过点的切线互相垂直,垂足为连接并延长,交的延长线于点.
求证:;
若,,求的长.
答案
1.【答案】
【解析】解:当时,如图:连接,
是的直径,
,
,
,
是的中位线,
,
,
,
是的切线.
所以B正确.
当时,,是的中位线,
是的切线.
所以C正确.
当时,,.
是的切线.
所以D正确.
故选A.
2.【答案】
【解析】解:与相切于点,
,
,
,
,
,
平分,
,
,
,
,
,
,
,,,
,
;
故选:.
3.【答案】
【解析】解:,是的两条切线,,为切点,
,所以正确;
,,
垂直平分,所以正确;
,是的两条切线,,为切点,
,,
,
点、在以为直径的圆上,
四边形有外接圆,所以正确;
只有当时,,此时,
不一定为外接圆的圆心,所以错误.
故选:.
4.【答案】
【解析】
解:连接,
是的切线,
,
,
,
,
,
,
,
由圆周角定理得,,
故选B.
5.【答案】
【解析】解:连结.
为的直径,为的切线,
,
,
,.
又,
,
.
在和中,,
≌,
.
又点在上,
是的切线;故正确,
≌,
,
,
垂直平分,
即,故正确;
为的直径,为的切线,
,
,
,
,
,
,
,
∽,故正确;
,
,
∽,
,
,
,故正确;
故选:.
6.【答案】
【解析】解:设三角板与圆的切点为,连接、,
由切线长定理知,平分,
,
在中,,
光盘的直径为,
故选:
7.【答案】
【解析】解:为的切线,
,
,
,
,
,
,
,
故选:.
8.【答案】
【解析】解:连接,
与相切于点,
,
,
,
∽,
,
设,则,
解得:,
故.
故选:.
9.【答案】
解:设与相交于点,是的直径,,,在中,,.直线是的切线,,又,,四边形为矩形,.
10.【答案】
解:如图,连接
为的切线,.
中,为中点,
,B.
,,,
,.
为的中点,为的中点,
.
中,,
,
在中,.
11.【答案】
解:,分别与圆相切于点,,
,,
在菱形中,,
点是的中点,,
,,
又,,
在四边形中,.
12.【答案】
解:连接并延长,交上一点,以为圆心,以为半径作,交轴于、,此时的长度最大,
,
,
以点为圆心的圆与轴相切.
的半径为,
,
,
是直径,
长度的最大值为,
故答案为.
13.【答案】
【解析】解:是的直径,与相切于点,
,
,
,
设,,
,
,
,
故答案为:.
14.【答案】
【解析】解:连接,
是的切线,
,
,
,
,
,,
,
,
,
,
,
故答案为:
15.【答案】
【解析】解:是的切线,
,
,
,
,
即的度数为,
故答案为:.
16.【答案】证明:是半圆的直径,
,
在与中,,
≌;
解:,由知,
,
是半圆所在圆的切线,
,
,
由知,
,
,
,
,,
,
平分.
17.【答案】解:如图,连接.
与相切于点,
,即.
,
.
在中,,
.
为的中点,
,即.
在中,由,得.
.
是的一个外角,
18.【答案】证明:连接,则,
,
又为的直径,,
,,
又,,
,即.
解:在和中,,
,,
,,,
,
.
19.【答案】证明:与相切于点,为的直径,
.
.
又,
.
E.
解:连接.
为的直径,.
,,.
又,,
.
...
20.【答案】解:连接,,如图,
在和中,,
≌,
,
是的切线,
,
,
直线是的切线;
过作于点,如图,
则
、都是的切线,
,
四边形是矩形,
,,
是的切线,
,,
,
,
,
即,
.
21.【答案】证明:是的直径,
,
,
,,
,
,即,
,
是的直径,
是的切线;
证明:平分,
,
,
,
,
∽,
,
.
22.【答案】解:证明:与相切于点,
,,
,
,
,
为的直径,
,
,
,
;
,
四边形是矩形,
,,
,,
,,
设的为,
,
,
即,
解得,,
,
即直径的长是.
23.【答案】证明:连结,,如图:
是的直径,
,
,
,
,
点是弧的中点,
,
,
为半径,
直线是的切线;
解:,
,
∽,
,
,,
,,
,
,
,,
,即,
解得:,
.
24.【答案】解:连接,如图,
过点作半圆的切线,交于点,
,
,
,
,
,
,
,
,
;
连接,,如图,
设圆的半径为,则,
,,,
,,
,
,
.
故圆的半径为.
25.【答案】证明:圆心在上,
是圆的直径,
,
连接,
平分,
,
,
,即,
,
,
为圆的半径,
是圆的切线;
证明:,
,
,
,
,,
,
∽;
解:为直角三角形,
,
,
,,
,
垂直平分,
,
为圆的直径,
,
在中,,即,
,
∽,
,
则.
26.【答案】解:连接,
为的直径,
,
,
,
,
,
是的切线,为切点,
,
,
,
,
,
;
,,
是的中位线,
,,
,
设,,
,
,
,
∽,
,
,
,
.
27.【答案】解:Ⅰ连接、,
,是的切线,
,
,
由圆周角定理得,;
Ⅱ连接,
为的直径,
,
,
,
,
,
,
.
28.【答案】解:连接,
是的直径,
,
,
,
,
,
,
,
,
,
,
是的切线;
,,,
≌,
,
又,
;
,,
∽,
,
,
,
,
设,,由勾股定理可得:,
解得:,
.
29.【答案】证明:连接,
,
,
平分,
,
,
,
,
,
与相切;
解:是的直径,
,
,
,
平分,
,
∽,
,
,
;
解:,理由如下:
过作于,
平分,,
,
在与中,
,
≌,
,
又,,
≌,
,
,
,
.
30.【答案】证明:连接、,如图,
为切线,
,
,
,
,
,
,
,
;
解:为直径,
,
,
,,
,
,
.
一、选择题
如图,是的直径,交于点,于点,要使是的切线,还需补充一个条件,则补充的条件不正确的是
A. B.
C. D.
如图,在中,是边上的点,以为圆心,为半径的与相切于点,平分,,,的长是
A. B. C. D.
如图,已知,是的两条切线,,为切点,线段交于点给出下列四种说法:
;
;
四边形有外接圆;
是外接圆的圆心.
其中正确说法的个数是
B. C. D.
如图,是的切线,点为切点,交于点,,点在上,则等于
B. C. D.
如图,为的直径,为的切线,弦,直线交的延长线于点,连接下列结论:是的切线;;∽;其中正确结论的个数有
个 B. 个 C. 个 D. 个
如图,一把直尺,的直角三角板和光盘如图摆放,为角与直尺交点,,则光盘的直径是
B. C. D.
如图,为的切线,切点为连接、,与交于点,延长与交于点,连接若,则的度数为
B. C. D.
如图,已知是的直径,点在的延长线上,与相切于点,过点作的垂线交的延长线于点,若的半径为,,则的长为
A. B. C. D.
如图,为的直径,直线与相切于点,,垂足为,交于点,连接、若,,则线段的长为 .
如图,在中,,,,点是的中点,以为直径作,分别与,交于点,,过点作的切线,交于点,则的长为 .
如图,菱形的边,分别与相切于点,若点是的中点,则 .
如图,在平面直角坐标系中,已知,以点为圆心的圆与轴相切.点、在轴上,且点为上的动点,,则长度的最大值为______.
如图,已知是的直径,与相切于点,连接,若,则______.
如图,是的弦,点在过点的切线上,且,交于点,已知,则______.
如图,已知是的直径,是的切线,连接交于点,连接若,则的度数是______
如图,是半圆的直径,,是半圆上不同于,的两点,,与相交于点是半圆所在圆的切线,与的延长线相交于点.
求证:≌;
若,求证:平分.
在中,为直径,为上一点.
如图,过点作的切线,与的延长线相交于点,若,求的大小
如图,为上一点,且经过的中点,连接并延长,与的延长线相交于点,若,求的大小.
如图,是的直径,为的弦,,与的延长线交于点,过点的切线交于点.
求证:
若,,求线段的长.
如图,是的直径,是的弦,过点作的切线,与的延长线交于点,作交于点.
求证:
若的半径为,,求的长.
如图,是的直径,和是它的两条切线,过上一点作直线,分别交、于点、,且.
求证:直线是的切线;
求证:.
已知:如图,是的直径,点为上一点,点是上一点,连接并延长至点,使,与交于点.
求证:是的切线;
若平分,求证:.
如图,为的直径,为上一点,和过点的切线互相垂直,垂足为,且交于点连接,,相交于点.
求证:;
若,,求直径的长.
如图,已知是的直径,经过的直角边上的点,交边于点,点是弧的中点,,连接.
求证:直线是切线.
若,,求的值.
如图,在中,,点在上,以为半径的半圆交于点,交于点,过点作半圆的切线,交于点.
求证:;
若,,,求半圆的半径长.
如图,是的外接圆,点在边上,的平分线交于点,连接、,过点作的平行线,与的延长线相交于点.
求证:是的切线;
求证:∽;
当,时,求线段的长.
如图,为的直径,为延长线上一点,是的切线,为切点,于点,交于点.
求证:;
若,,求的长.
已知,分别与相切于点,,,为上一点.
Ⅰ如图,求的大小;
Ⅱ如图,为的直径,与相交于点若,求的大小.
如图,是的直径,点在的延长线上,、是上的两点,,,延长交的延长线于点.
求证:是的切线;
求证:;
若,,求弦的长.
如图,点在以为直径的上,平分交于点,过作的垂线,垂足为.
求证:与相切;
若,,求的长;
请用线段、表示的长,并说明理由
如图,为的直径,点在上,与过点的切线互相垂直,垂足为连接并延长,交的延长线于点.
求证:;
若,,求的长.
答案
1.【答案】
【解析】解:当时,如图:连接,
是的直径,
,
,
,
是的中位线,
,
,
,
是的切线.
所以B正确.
当时,,是的中位线,
是的切线.
所以C正确.
当时,,.
是的切线.
所以D正确.
故选A.
2.【答案】
【解析】解:与相切于点,
,
,
,
,
,
平分,
,
,
,
,
,
,
,,,
,
;
故选:.
3.【答案】
【解析】解:,是的两条切线,,为切点,
,所以正确;
,,
垂直平分,所以正确;
,是的两条切线,,为切点,
,,
,
点、在以为直径的圆上,
四边形有外接圆,所以正确;
只有当时,,此时,
不一定为外接圆的圆心,所以错误.
故选:.
4.【答案】
【解析】
解:连接,
是的切线,
,
,
,
,
,
,
,
由圆周角定理得,,
故选B.
5.【答案】
【解析】解:连结.
为的直径,为的切线,
,
,
,.
又,
,
.
在和中,,
≌,
.
又点在上,
是的切线;故正确,
≌,
,
,
垂直平分,
即,故正确;
为的直径,为的切线,
,
,
,
,
,
,
,
∽,故正确;
,
,
∽,
,
,
,故正确;
故选:.
6.【答案】
【解析】解:设三角板与圆的切点为,连接、,
由切线长定理知,平分,
,
在中,,
光盘的直径为,
故选:
7.【答案】
【解析】解:为的切线,
,
,
,
,
,
,
,
故选:.
8.【答案】
【解析】解:连接,
与相切于点,
,
,
,
∽,
,
设,则,
解得:,
故.
故选:.
9.【答案】
解:设与相交于点,是的直径,,,在中,,.直线是的切线,,又,,四边形为矩形,.
10.【答案】
解:如图,连接
为的切线,.
中,为中点,
,B.
,,,
,.
为的中点,为的中点,
.
中,,
,
在中,.
11.【答案】
解:,分别与圆相切于点,,
,,
在菱形中,,
点是的中点,,
,,
又,,
在四边形中,.
12.【答案】
解:连接并延长,交上一点,以为圆心,以为半径作,交轴于、,此时的长度最大,
,
,
以点为圆心的圆与轴相切.
的半径为,
,
,
是直径,
长度的最大值为,
故答案为.
13.【答案】
【解析】解:是的直径,与相切于点,
,
,
,
设,,
,
,
,
故答案为:.
14.【答案】
【解析】解:连接,
是的切线,
,
,
,
,
,,
,
,
,
,
,
故答案为:
15.【答案】
【解析】解:是的切线,
,
,
,
,
即的度数为,
故答案为:.
16.【答案】证明:是半圆的直径,
,
在与中,,
≌;
解:,由知,
,
是半圆所在圆的切线,
,
,
由知,
,
,
,
,,
,
平分.
17.【答案】解:如图,连接.
与相切于点,
,即.
,
.
在中,,
.
为的中点,
,即.
在中,由,得.
.
是的一个外角,
18.【答案】证明:连接,则,
,
又为的直径,,
,,
又,,
,即.
解:在和中,,
,,
,,,
,
.
19.【答案】证明:与相切于点,为的直径,
.
.
又,
.
E.
解:连接.
为的直径,.
,,.
又,,
.
...
20.【答案】解:连接,,如图,
在和中,,
≌,
,
是的切线,
,
,
直线是的切线;
过作于点,如图,
则
、都是的切线,
,
四边形是矩形,
,,
是的切线,
,,
,
,
,
即,
.
21.【答案】证明:是的直径,
,
,
,,
,
,即,
,
是的直径,
是的切线;
证明:平分,
,
,
,
,
∽,
,
.
22.【答案】解:证明:与相切于点,
,,
,
,
,
为的直径,
,
,
,
;
,
四边形是矩形,
,,
,,
,,
设的为,
,
,
即,
解得,,
,
即直径的长是.
23.【答案】证明:连结,,如图:
是的直径,
,
,
,
,
点是弧的中点,
,
,
为半径,
直线是的切线;
解:,
,
∽,
,
,,
,,
,
,
,,
,即,
解得:,
.
24.【答案】解:连接,如图,
过点作半圆的切线,交于点,
,
,
,
,
,
,
,
,
;
连接,,如图,
设圆的半径为,则,
,,,
,,
,
,
.
故圆的半径为.
25.【答案】证明:圆心在上,
是圆的直径,
,
连接,
平分,
,
,
,即,
,
,
为圆的半径,
是圆的切线;
证明:,
,
,
,
,,
,
∽;
解:为直角三角形,
,
,
,,
,
垂直平分,
,
为圆的直径,
,
在中,,即,
,
∽,
,
则.
26.【答案】解:连接,
为的直径,
,
,
,
,
,
是的切线,为切点,
,
,
,
,
,
;
,,
是的中位线,
,,
,
设,,
,
,
,
∽,
,
,
,
.
27.【答案】解:Ⅰ连接、,
,是的切线,
,
,
由圆周角定理得,;
Ⅱ连接,
为的直径,
,
,
,
,
,
,
.
28.【答案】解:连接,
是的直径,
,
,
,
,
,
,
,
,
,
,
是的切线;
,,,
≌,
,
又,
;
,,
∽,
,
,
,
,
设,,由勾股定理可得:,
解得:,
.
29.【答案】证明:连接,
,
,
平分,
,
,
,
,
,
与相切;
解:是的直径,
,
,
,
平分,
,
∽,
,
,
;
解:,理由如下:
过作于,
平分,,
,
在与中,
,
≌,
,
又,,
≌,
,
,
,
.
30.【答案】证明:连接、,如图,
为切线,
,
,
,
,
,
,
,
;
解:为直径,
,
,
,,
,
,
.
