新疆维吾尔自治区疏附县第一中学2021-2022学年高二上学期第二次月考(12月)数学试题(Word版含答案)
文档属性
| 名称 | 新疆维吾尔自治区疏附县第一中学2021-2022学年高二上学期第二次月考(12月)数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 347.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 08:47:43 | ||
图片预览


文档简介
疏附县第一中学2021-2022学年高二上学期第二次月考
数学试题
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从个体编号为的总体中,用系统抽样(等距)的方法抽取个个体,若抽取的第一个个体的编号为则抽取的最后一个个体的编号为( )
A. B. C. D.
2.直线经过点,在轴上的截距的取值范围是,则其斜率的取值范围是( )
A. B.
C. D.
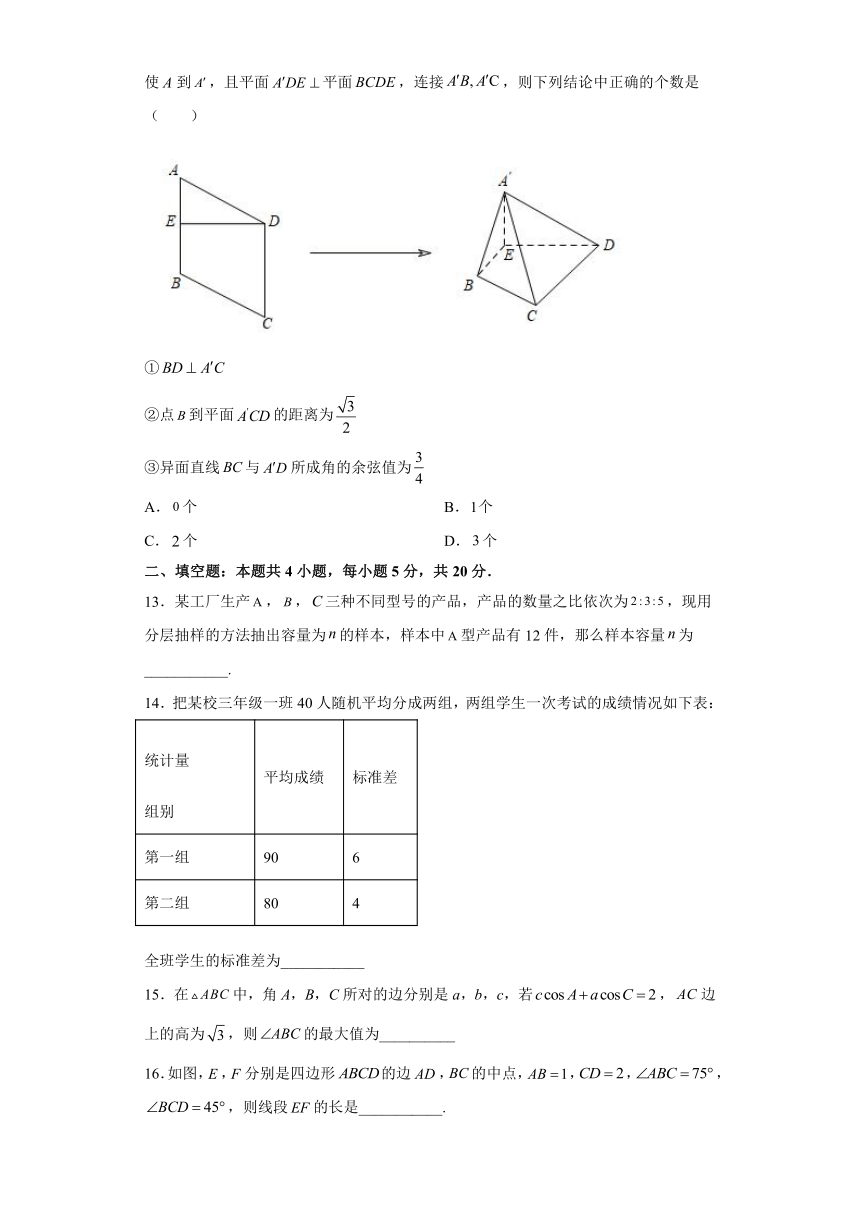
3.更相减损术是出自中国古代数学专著《九章算术》的一种求最大公约数算法,下图是该算法的程序框图,如果输入,,则输出的a值是( )
A.17 B.34 C.36 D.68
4.已知点,过点作直线(,不同时为0)的垂线,垂足为,则的最小值为( )
A. B. C. D.
5.在三棱锥中,,,,点是的中点,底面,则点到平面的距离为( )
A. B. C. D.
6.平行六面体(底面是平行四边形的棱柱)中,,,,则( )
A. B. C. D.
7.经过圆:的圆心,并且与直线垂直的直线方程( )
A. B.
C. D.
8.已知双曲线的一条渐近线与直线x-2y+3=0垂直,则a=( )
A. B. C. D.
9.已知圆,从动圆上的动点向圆引切线,切点分别是,,则的最小值是( )
A. B. C. D.
10.某校组织全体学生参加了主题为“建党百年,薪火相传”的知识竞赛,随机抽取了200名学生进行成绩统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示,下列说法正确的是( )
A.直方图中的值为0.004
B.在被抽取的学生中,成绩在区间[70,80)的学生数为15人
C.估计全校学生成绩的样本数据的80%分位数约为93分
D.估计全校学生的平均成绩为84分
11.若一动点在曲线上移动,则它和定点的连线的中点的轨迹方程是( )
A. B.
C. D.
12.如图,菱形边长为2,,为边的中点,将沿折起,使A到,且平面平面,连接,则下列结论中正确的个数是( )
①
②点到平面的距离为
③异面直线与所成角的余弦值为
A.个 B.个
C.个 D.个
二、填空题:本题共4小题,每小题5分,共20分.
13.某工厂生产,,三种不同型号的产品,产品的数量之比依次为,现用分层抽样的方法抽出容量为的样本,样本中型产品有12件,那么样本容量为___________.
14.把某校三年级一班40人随机平均分成两组,两组学生一次考试的成绩情况如下表:
统计量 组别 平均成绩 标准差
第一组 90 6
第二组 80 4
全班学生的标准差为___________
15.在中,角A,B,C所对的边分别是a,b,c,若,边上的高为,则的最大值为__________
16.如图,,分别是四边形的边,的中点,,,,,则线段的长是___________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
在平面直角坐标系中,已知的三个顶点,,.
(1)求边所在直线的方程;
(2)边上中线的方程为,且的面积等于,求点的坐标.
18.(本小题满分12分)
发展特色农业是我国农业结构战略调整的要求,某县为了响应国家的号召,特地承包了一块土地,已知土地的使用面积x(单位:公顷)与相应的管理时间y(单位:月)的关系如下表所示:
土地使用面积x 1 2 3 4 5
管理时间y 8 11 14 24 23
调查了某村300名村民参与管理的意愿,得到列联表的部分数据如下表所示:
愿意参与管理 不愿意参与管理 总计
男性村民 140 60
女性村民 40
总计
(1)画出散点图,判断土地使用面积x与管理时间y是否线性相关,并根据相关系数r说明相关关系的强弱;(若,认为两个变量有很强的线性相关性,r值精确到0.001)
(2)补全列联表,并判断是否有99.9%的把握认为该村的村民的参与管理意愿与性别有关.
参考公式:
参考数据:,,.
19.(本小题满分12分)
抛物线的焦点F是圆x2+y2-4x=0的圆心.
(1)求该抛物线的标准方程;
(2)直线l的斜率为2,且过抛物线的焦点,若l与抛物线、圆依次交于A、B、C、D,求|AB|+|CD|.
20.(本小题满分12分)
如图所示,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点.
(1)求BN的长;
(2)求A1B与B1C所成角的余弦值.
21.(本小题满分12分)
如图所示,在三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=AC,四边形BCC1B1为菱形,BC=2,∠BCC1=,D为B1C1的中点.
(1)证明:B1C1⊥平面A1DB;
(2)若AC1=2,求二面角C1﹣A1B1﹣C的余弦值.
22.(本小题满分12分)
函数的定义域且,对定义域D内任意两个实数,,都有成立.
(1)求的值并证明为偶函数;
(2)若时,,解关于x的不等式.
(3)若时,,且不等式对任意实数x恒成立,求非零实数a的取值范围.
答案
1.B2.D3.B4.B5.A6.C7.D8.A9.D10.D11.C12.C
13.60
14.
15.
16.
17.
(1)
(2)或
18.(1)散点图见解析,相关,线性相关性很强;(2)列联表见解析,有把握.
19.(1)y2=8x;(2)6.
20.
(1)
(2)
21.
(1)证明见解析
(2)
22.
(1),证明见解析
(2)
(3)
数学试题
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从个体编号为的总体中,用系统抽样(等距)的方法抽取个个体,若抽取的第一个个体的编号为则抽取的最后一个个体的编号为( )
A. B. C. D.
2.直线经过点,在轴上的截距的取值范围是,则其斜率的取值范围是( )
A. B.
C. D.
3.更相减损术是出自中国古代数学专著《九章算术》的一种求最大公约数算法,下图是该算法的程序框图,如果输入,,则输出的a值是( )
A.17 B.34 C.36 D.68
4.已知点,过点作直线(,不同时为0)的垂线,垂足为,则的最小值为( )
A. B. C. D.
5.在三棱锥中,,,,点是的中点,底面,则点到平面的距离为( )
A. B. C. D.
6.平行六面体(底面是平行四边形的棱柱)中,,,,则( )
A. B. C. D.
7.经过圆:的圆心,并且与直线垂直的直线方程( )
A. B.
C. D.
8.已知双曲线的一条渐近线与直线x-2y+3=0垂直,则a=( )
A. B. C. D.
9.已知圆,从动圆上的动点向圆引切线,切点分别是,,则的最小值是( )
A. B. C. D.
10.某校组织全体学生参加了主题为“建党百年,薪火相传”的知识竞赛,随机抽取了200名学生进行成绩统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示,下列说法正确的是( )
A.直方图中的值为0.004
B.在被抽取的学生中,成绩在区间[70,80)的学生数为15人
C.估计全校学生成绩的样本数据的80%分位数约为93分
D.估计全校学生的平均成绩为84分
11.若一动点在曲线上移动,则它和定点的连线的中点的轨迹方程是( )
A. B.
C. D.
12.如图,菱形边长为2,,为边的中点,将沿折起,使A到,且平面平面,连接,则下列结论中正确的个数是( )
①
②点到平面的距离为
③异面直线与所成角的余弦值为
A.个 B.个
C.个 D.个
二、填空题:本题共4小题,每小题5分,共20分.
13.某工厂生产,,三种不同型号的产品,产品的数量之比依次为,现用分层抽样的方法抽出容量为的样本,样本中型产品有12件,那么样本容量为___________.
14.把某校三年级一班40人随机平均分成两组,两组学生一次考试的成绩情况如下表:
统计量 组别 平均成绩 标准差
第一组 90 6
第二组 80 4
全班学生的标准差为___________
15.在中,角A,B,C所对的边分别是a,b,c,若,边上的高为,则的最大值为__________
16.如图,,分别是四边形的边,的中点,,,,,则线段的长是___________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
在平面直角坐标系中,已知的三个顶点,,.
(1)求边所在直线的方程;
(2)边上中线的方程为,且的面积等于,求点的坐标.
18.(本小题满分12分)
发展特色农业是我国农业结构战略调整的要求,某县为了响应国家的号召,特地承包了一块土地,已知土地的使用面积x(单位:公顷)与相应的管理时间y(单位:月)的关系如下表所示:
土地使用面积x 1 2 3 4 5
管理时间y 8 11 14 24 23
调查了某村300名村民参与管理的意愿,得到列联表的部分数据如下表所示:
愿意参与管理 不愿意参与管理 总计
男性村民 140 60
女性村民 40
总计
(1)画出散点图,判断土地使用面积x与管理时间y是否线性相关,并根据相关系数r说明相关关系的强弱;(若,认为两个变量有很强的线性相关性,r值精确到0.001)
(2)补全列联表,并判断是否有99.9%的把握认为该村的村民的参与管理意愿与性别有关.
参考公式:
参考数据:,,.
19.(本小题满分12分)
抛物线的焦点F是圆x2+y2-4x=0的圆心.
(1)求该抛物线的标准方程;
(2)直线l的斜率为2,且过抛物线的焦点,若l与抛物线、圆依次交于A、B、C、D,求|AB|+|CD|.
20.(本小题满分12分)
如图所示,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别为A1B1,A1A的中点.
(1)求BN的长;
(2)求A1B与B1C所成角的余弦值.
21.(本小题满分12分)
如图所示,在三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=AC,四边形BCC1B1为菱形,BC=2,∠BCC1=,D为B1C1的中点.
(1)证明:B1C1⊥平面A1DB;
(2)若AC1=2,求二面角C1﹣A1B1﹣C的余弦值.
22.(本小题满分12分)
函数的定义域且,对定义域D内任意两个实数,,都有成立.
(1)求的值并证明为偶函数;
(2)若时,,解关于x的不等式.
(3)若时,,且不等式对任意实数x恒成立,求非零实数a的取值范围.
答案
1.B2.D3.B4.B5.A6.C7.D8.A9.D10.D11.C12.C
13.60
14.
15.
16.
17.
(1)
(2)或
18.(1)散点图见解析,相关,线性相关性很强;(2)列联表见解析,有把握.
19.(1)y2=8x;(2)6.
20.
(1)
(2)
21.
(1)证明见解析
(2)
22.
(1),证明见解析
(2)
(3)
同课章节目录
