人教高中数学必修二1.3.2 球的体积和表面积 球的内切和外接问题课件(共22张PPT)
文档属性
| 名称 | 人教高中数学必修二1.3.2 球的体积和表面积 球的内切和外接问题课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 895.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 21:03:46 | ||
图片预览






文档简介
(共22张PPT)
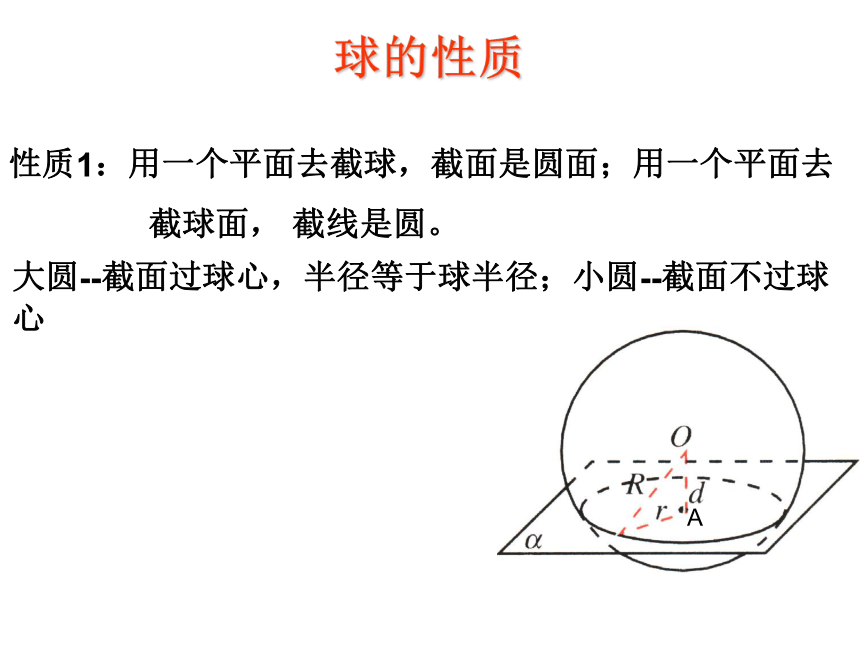
球的旋转定义:
1.半圆以它的直径所在的直线为轴旋转所成的曲面叫做球面。
2.半圆面以它的
直径所在的直线
为轴旋转所成的
几何体叫做球体。
(球是旋转体 )
3.注意:球面和球体的区别:
球面仅仅是指球的表面,
而球体不仅包括球的表面,
而且还包括球面所围成的几何空间。
球心
球的半径
球的直径
球的性质
性质1:用一个平面去截球,截面是圆面;用一个平面去
截球面, 截线是圆。
大圆--截面过球心,半径等于球半径;小圆--截面不过球心
A
2、球心和截面圆心的连线垂直于截面
O
A
B
C
D
d
r
R
3、球心到截面的距离与球的半径R及截面的半径的关系:
性质1:用一个平面去截球,截面是圆面;用一个平面去
截球面, 截线是圆。
大圆--截面过球心,半径等于球半径;小圆--截面不过球心
球的半径r和正方体
的棱长a有什么关系?
.
r
a
球与多面体的内切、外接
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个 。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个 。
一、
球体的体积与表面积
①
②
多面体的外接球
多面体的内切球
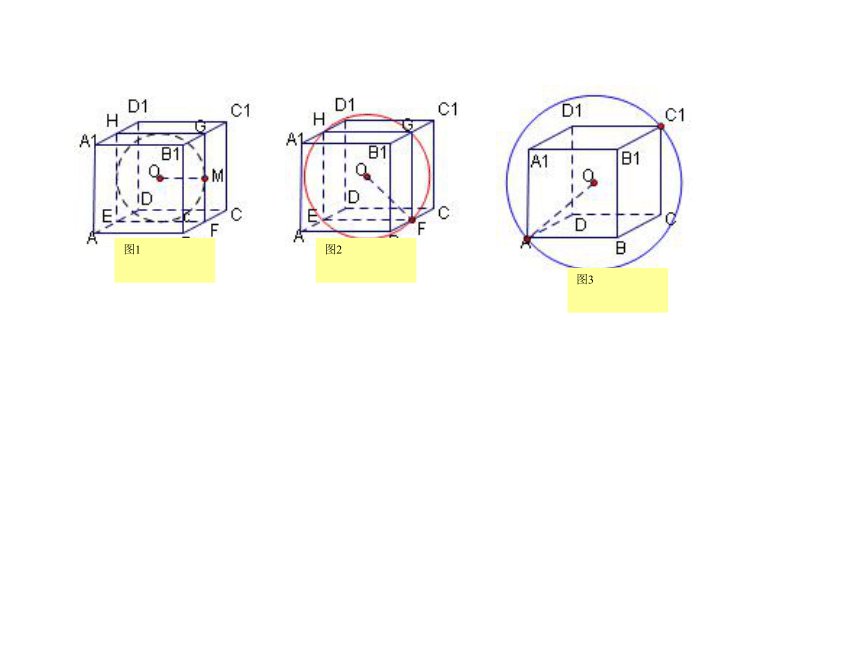
图1
图2
图3
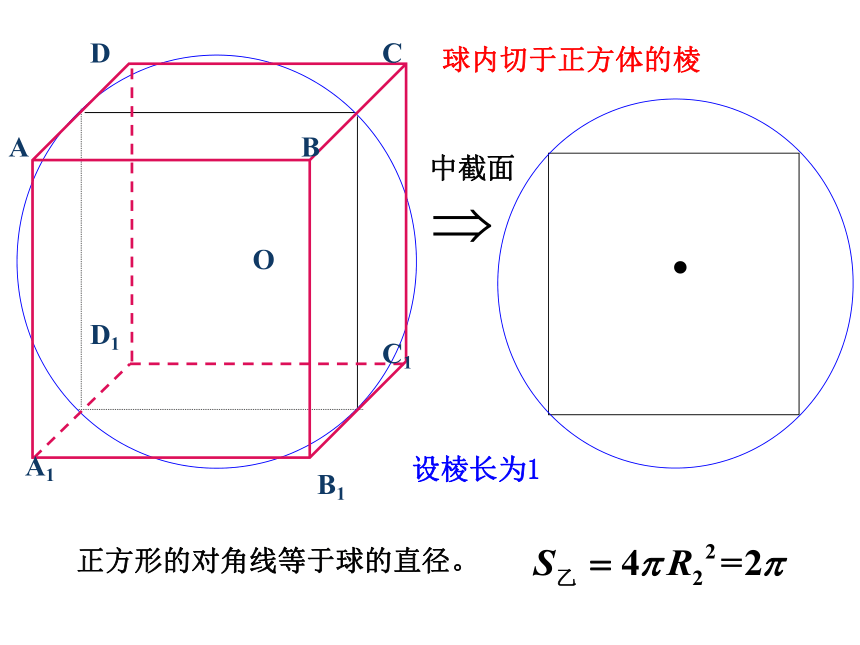
中截面
设棱长为1
球的外切正方体的棱长等于球直径。
A
B
C
D
D1
C1
B1
A1
O
例1 甲球内切于正方体的各面,乙球内切于该正方体的各条棱, 丙球外接于该正方体,则三球表面面积之比为( ) A. 1:2:3 B. C. D.
球与棱柱的组合体问题
A
B
C
D
D1
C1
B1
A1
O
中截面
正方形的对角线等于球的直径。
.
球内切于正方体的棱
设棱长为1
A
B
C
D
D1
C1
A1
O
B1
对角面
球的内接正方体的对角线等于球直径。
球外接于正方体
设棱长为1
2、求长方体的外接球的有关问题
例2、一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .
解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。长方体体对角线长为 ,故球的表面积为 .
变式题:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( )
A. B. C. D.
C
如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.
一、直接法
变式题:一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为 .
1、求正方体的外接球的有关问题
例1、若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为 .
A
C
B
P
O
二、构造法 1、构造正方体
例2、若三棱锥的三条侧棱两两垂直,且侧棱长均为 ,则其外接球的表面积是
变式题(浙江高考题)已知球O的面上四点A、B、C、D, 则球O的体积等于
图4
A
B
C
D
O
A
B
C
D
O
求正多面体外接球的半径
求正方体外接球的半径
例3、 求棱长为 a 的正四面体 P – ABC 的外接球的表面积。
变式题:1、一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为( )
A. B. C. D.
A
2、在等腰梯形ABCD中,
E为AB的中点,将 分布沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
图3
C
三、确定球心位置法
在矩形ABCD中,AB=4,BC=3,AC沿将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为( )
C
四、公式法
一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为 ,底面周长为3,则这个球的体积为
解 : 设正六棱柱的底面边长为x,高为h,则有
∴正六棱柱的底面圆的半径 ,球心到底面的距离
.∴外接球的半径
小结 本题是运用公式 求球的半径的,该公式是求球的半径的常用公式.
思考题:半径为R的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为________,体积为________.
五、构造直角三角形
例1、求棱长为1的正四面体外接球的体积.
六、寻求轴截面圆半径法
正四棱锥S-ABCD的底面边长和各侧棱长都为 ,点S,A,B,C,D都在同一球面上,则此球的体积为 .
解 设正四棱锥的底面中心为 ,外接球的球心为O,如图3所示.∴由球的截面的性质,
可得
又 ,∴球心O必在 所在的直线上.
∴ 的外接圆就是外接球的一个轴截面圆,外接圆的半径就是外接球的半径.
在 中,由
是外接圆的半径,也是外接球的半径.故
几何体的内切球
正四面体的棱长为a,则其内切球和外接球的半径是多少?
图1
解:如图1所示,设点o是内切球的球心,正四面体棱长为a.由图形的对称性知,点o也是外接球的球心.设内切球半径为r,外接球半径为R.
正四面体的表面积
正四面体的体积
在 中, 即 ,得 得
【点评】由于正四面体本身的对称性可知,内切球和外接球的两个球心是重合的,为正四面体高的四等分点,即内切球的半径为 (h 为正四面体的高),且外接球的半径 ,从而可以通过截面图中 建立棱长与半径之间的关系。
(1)正多面体存在内切球且正多面体的中心为内切球的球心.
(2)求多面体内切球半径,往往可用“等体积法”.
(3)正四面体内切球半径是高的 ,外接球半径是高的 .
(4)并非所有多面体都有内切球(或外接球).
球的内切、外接问题
5、体积分割是求内切球半径的通用做法。
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不 重合。
4、基本方法:构造三角形利用相似比和勾股定理。
球的旋转定义:
1.半圆以它的直径所在的直线为轴旋转所成的曲面叫做球面。
2.半圆面以它的
直径所在的直线
为轴旋转所成的
几何体叫做球体。
(球是旋转体 )
3.注意:球面和球体的区别:
球面仅仅是指球的表面,
而球体不仅包括球的表面,
而且还包括球面所围成的几何空间。
球心
球的半径
球的直径
球的性质
性质1:用一个平面去截球,截面是圆面;用一个平面去
截球面, 截线是圆。
大圆--截面过球心,半径等于球半径;小圆--截面不过球心
A
2、球心和截面圆心的连线垂直于截面
O
A
B
C
D
d
r
R
3、球心到截面的距离与球的半径R及截面的半径的关系:
性质1:用一个平面去截球,截面是圆面;用一个平面去
截球面, 截线是圆。
大圆--截面过球心,半径等于球半径;小圆--截面不过球心
球的半径r和正方体
的棱长a有什么关系?
.
r
a
球与多面体的内切、外接
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个 。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个 。
一、
球体的体积与表面积
①
②
多面体的外接球
多面体的内切球
图1
图2
图3
中截面
设棱长为1
球的外切正方体的棱长等于球直径。
A
B
C
D
D1
C1
B1
A1
O
例1 甲球内切于正方体的各面,乙球内切于该正方体的各条棱, 丙球外接于该正方体,则三球表面面积之比为( ) A. 1:2:3 B. C. D.
球与棱柱的组合体问题
A
B
C
D
D1
C1
B1
A1
O
中截面
正方形的对角线等于球的直径。
.
球内切于正方体的棱
设棱长为1
A
B
C
D
D1
C1
A1
O
B1
对角面
球的内接正方体的对角线等于球直径。
球外接于正方体
设棱长为1
2、求长方体的外接球的有关问题
例2、一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .
解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。长方体体对角线长为 ,故球的表面积为 .
变式题:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( )
A. B. C. D.
C
如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.
一、直接法
变式题:一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为 .
1、求正方体的外接球的有关问题
例1、若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为 .
A
C
B
P
O
二、构造法 1、构造正方体
例2、若三棱锥的三条侧棱两两垂直,且侧棱长均为 ,则其外接球的表面积是
变式题(浙江高考题)已知球O的面上四点A、B、C、D, 则球O的体积等于
图4
A
B
C
D
O
A
B
C
D
O
求正多面体外接球的半径
求正方体外接球的半径
例3、 求棱长为 a 的正四面体 P – ABC 的外接球的表面积。
变式题:1、一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为( )
A. B. C. D.
A
2、在等腰梯形ABCD中,
E为AB的中点,将 分布沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
图3
C
三、确定球心位置法
在矩形ABCD中,AB=4,BC=3,AC沿将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为( )
C
四、公式法
一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为 ,底面周长为3,则这个球的体积为
解 : 设正六棱柱的底面边长为x,高为h,则有
∴正六棱柱的底面圆的半径 ,球心到底面的距离
.∴外接球的半径
小结 本题是运用公式 求球的半径的,该公式是求球的半径的常用公式.
思考题:半径为R的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为________,体积为________.
五、构造直角三角形
例1、求棱长为1的正四面体外接球的体积.
六、寻求轴截面圆半径法
正四棱锥S-ABCD的底面边长和各侧棱长都为 ,点S,A,B,C,D都在同一球面上,则此球的体积为 .
解 设正四棱锥的底面中心为 ,外接球的球心为O,如图3所示.∴由球的截面的性质,
可得
又 ,∴球心O必在 所在的直线上.
∴ 的外接圆就是外接球的一个轴截面圆,外接圆的半径就是外接球的半径.
在 中,由
是外接圆的半径,也是外接球的半径.故
几何体的内切球
正四面体的棱长为a,则其内切球和外接球的半径是多少?
图1
解:如图1所示,设点o是内切球的球心,正四面体棱长为a.由图形的对称性知,点o也是外接球的球心.设内切球半径为r,外接球半径为R.
正四面体的表面积
正四面体的体积
在 中, 即 ,得 得
【点评】由于正四面体本身的对称性可知,内切球和外接球的两个球心是重合的,为正四面体高的四等分点,即内切球的半径为 (h 为正四面体的高),且外接球的半径 ,从而可以通过截面图中 建立棱长与半径之间的关系。
(1)正多面体存在内切球且正多面体的中心为内切球的球心.
(2)求多面体内切球半径,往往可用“等体积法”.
(3)正四面体内切球半径是高的 ,外接球半径是高的 .
(4)并非所有多面体都有内切球(或外接球).
球的内切、外接问题
5、体积分割是求内切球半径的通用做法。
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不 重合。
4、基本方法:构造三角形利用相似比和勾股定理。
