2021-2022学年黑龙江省哈尔滨市香坊区九年级(上)月考数学试卷(10月份)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年黑龙江省哈尔滨市香坊区九年级(上)月考数学试卷(10月份)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 552.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 08:10:14 | ||
图片预览

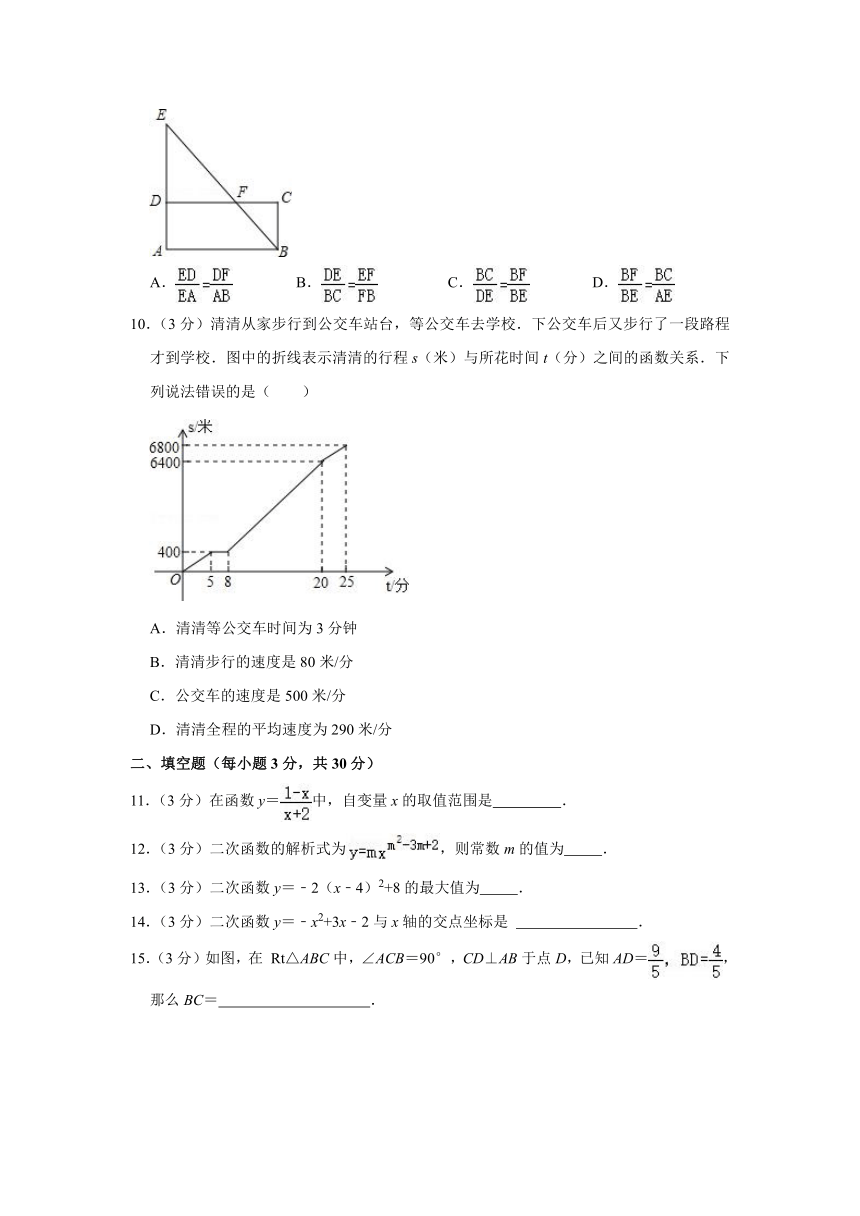

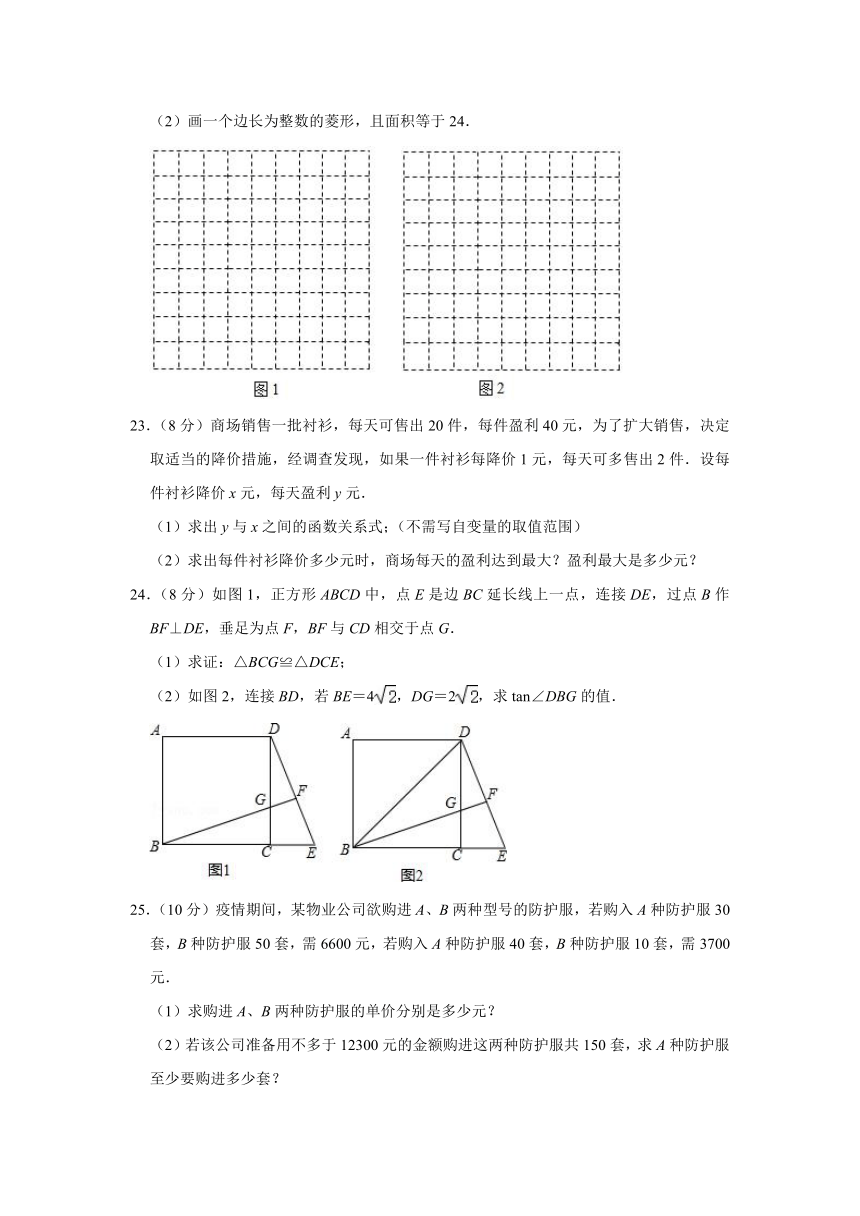
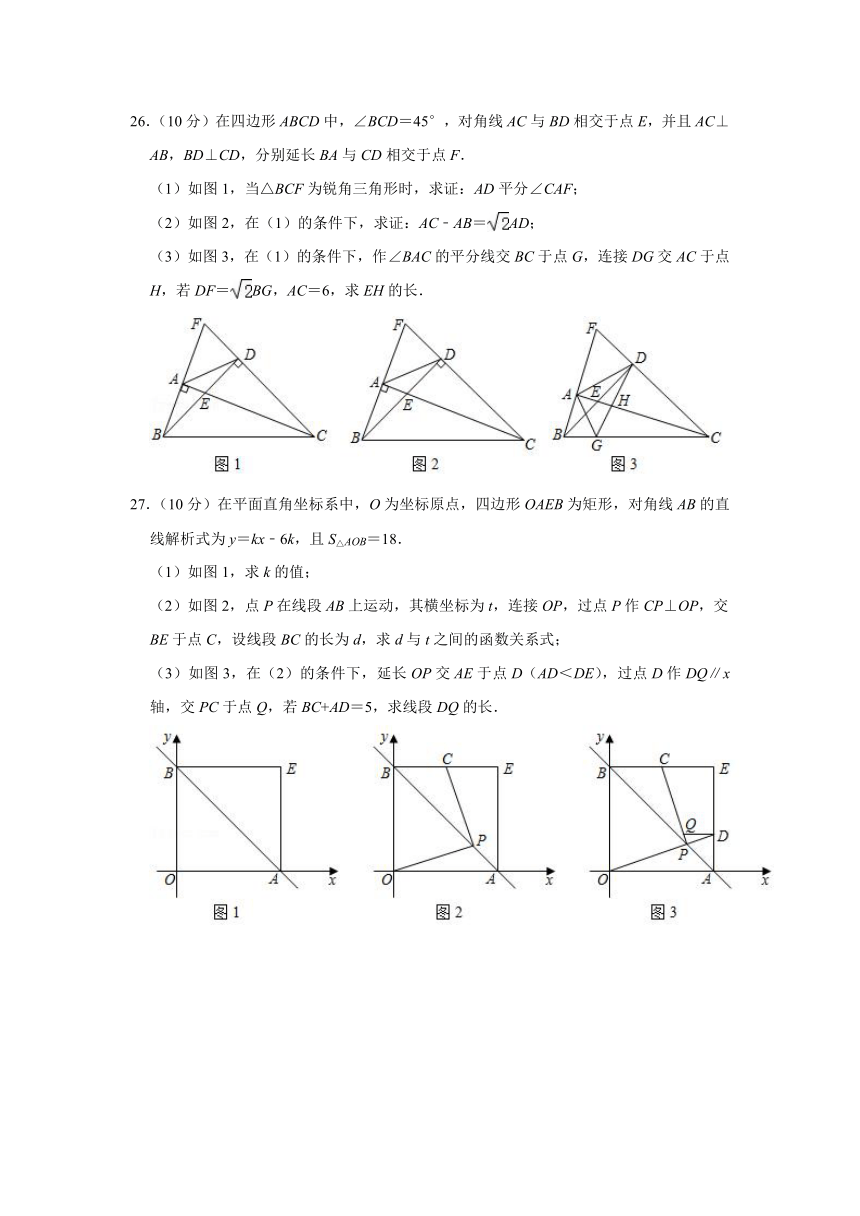
文档简介
2021-2022学年黑龙江省哈尔滨市香坊区九年级(上)月考数学试卷(10月份)(五四学制)
一、选择题(每小题3分共30分)
1.(3分)如果a与﹣2互为相反数,那么a等于( )
A.﹣2 B.2 C.﹣ D.
2.(3分)下列运算正确的是( )
A.a3 a2=a6 B.(x3)3=x6 C.x5+x5=x10 D.﹣a8÷a4=﹣a4
3.(3分)已知抛物线的解析式为y=﹣(x+2)2﹣3,则该抛物线的顶点坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
4.(3分)在Rt△ABC中,∠C=90°,若AB=2,AC=1,则tanA的值为( )
A. B. C. D.
5.(3分)将抛物线y=2(x﹣3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )
A.y=2(x﹣6)2 B.y=2(x﹣6)2+4
C.y=2x2 D.y=2x2+4
6.(3分)斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是( )
A.500 sinα米 B.米 C.500 cosα米 D.米
7.(3分)某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)=182
8.(3分)在△ABC中,∠C=90°,tanA=,则sinA=( )
A. B. C. D.
9.(3分)如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
10.(3分)清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校.图中的折线表示清清的行程s(米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A.清清等公交车时间为3分钟
B.清清步行的速度是80米/分
C.公交车的速度是500米/分
D.清清全程的平均速度为290米/分
二、填空题(每小题3分,共30分)
11.(3分)在函数y=中,自变量x的取值范围是 .
12.(3分)二次函数的解析式为,则常数m的值为 .
13.(3分)二次函数y=﹣2(x﹣4)2+8的最大值为 .
14.(3分)二次函数y=﹣x2+3x﹣2与x轴的交点坐标是 .
15.(3分)如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于点D,已知AD=,那么BC= .
16.(3分)汽车刹车后行驶的距离s(米)与行驶的时间t(秒)函数关系式是s=15t﹣6t2,汽车刹车后停下来前进了 米.
17.(3分)二次函数y=ax2+bx+c(0≤x≤3)的图象如图所示,则y的取值范围是 .
18.(3分)某商店老板将一件进价为800元的商品先提价50%,再打8折卖出,则卖出这件商品所获利润是 元.
19.(3分)等腰△ABC中,AB=AC,AD⊥BC于点D,点E在直线AC上,2CE=AC,若AD=6,BE=5,则BC= .
20.(3分)如图,在四边形ABCD中,∠ADC=∠ABC=90°,连接AC,BD,过点B作BE⊥AC,垂足为E,若∠BDC+∠DAB=90°,BE=4,CD=6,则BC= .
三、解答题(21~22题各7分,23题、24题各8分,25~27题各10分,共60分)
21.(7分)先化简,再求代数式的值,其中a=tan60°﹣6sin30°.
22.(7分)如图,图1,图2,均为正方形网格,每个小正方形的面积均为1.在这个正方形网格中,各个小正方形的顶点叫做格点.请在下面的网格中按要求画图,使得每个图形的顶点均在格点上.
(1)画一个直角三角形,且三边之比为1:2:;
(2)画一个边长为整数的菱形,且面积等于24.
23.(8分)商场销售一批衬衫,每天可售出20件,每件盈利40元,为了扩大销售,决定取适当的降价措施,经调查发现,如果一件衬衫每降价1元,每天可多售出2件.设每件衬衫降价x元,每天盈利y元.
(1)求出y与x之间的函数关系式;(不需写自变量的取值范围)
(2)求出每件衬衫降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
24.(8分)如图1,正方形ABCD中,点E是边BC延长线上一点,连接DE,过点B作BF⊥DE,垂足为点F,BF与CD相交于点G.
(1)求证:△BCG≌△DCE;
(2)如图2,连接BD,若BE=4,DG=2,求tan∠DBG的值.
25.(10分)疫情期间,某物业公司欲购进A、B两种型号的防护服,若购入A种防护服30套,B种防护服50套,需6600元,若购入A种防护服40套,B种防护服10套,需3700元.
(1)求购进A、B两种防护服的单价分别是多少元?
(2)若该公司准备用不多于12300元的金额购进这两种防护服共150套,求A种防护服至少要购进多少套?
26.(10分)在四边形ABCD中,∠BCD=45°,对角线AC与BD相交于点E,并且AC⊥AB,BD⊥CD,分别延长BA与CD相交于点F.
(1)如图1,当△BCF为锐角三角形时,求证:AD平分∠CAF;
(2)如图2,在(1)的条件下,求证:AC﹣AB=AD;
(3)如图3,在(1)的条件下,作∠BAC的平分线交BC于点G,连接DG交AC于点H,若DF=BG,AC=6,求EH的长.
27.(10分)在平面直角坐标系中,O为坐标原点,四边形OAEB为矩形,对角线AB的直线解析式为y=kx﹣6k,且S△AOB=18.
(1)如图1,求k的值;
(2)如图2,点P在线段AB上运动,其横坐标为t,连接OP,过点P作CP⊥OP,交BE于点C,设线段BC的长为d,求d与t之间的函数关系式;
(3)如图3,在(2)的条件下,延长OP交AE于点D(AD<DE),过点D作DQ∥x轴,交PC于点Q,若BC+AD=5,求线段DQ的长.
2021-2022学年黑龙江省哈尔滨市香坊区九年级(上)月考数学试卷(10月份)(五四学制)
参考答案与试题解析
一、选择题(每小题3分共30分)
1.(3分)如果a与﹣2互为相反数,那么a等于( )
A.﹣2 B.2 C.﹣ D.
【分析】一个数的相反数就是在这个数前面添上“﹣”号.
【解答】解:﹣2的相反数是2,那么a等于2.
故选:B.
2.(3分)下列运算正确的是( )
A.a3 a2=a6 B.(x3)3=x6 C.x5+x5=x10 D.﹣a8÷a4=﹣a4
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=a5,不符合题意;
B、原式=x9,不符合题意;
C、原式=2x5,不符合题意;
D、原式=﹣a4,符合题意,
故选:D.
3.(3分)已知抛物线的解析式为y=﹣(x+2)2﹣3,则该抛物线的顶点坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
【分析】根据题目中的抛物线的解析式,可以直接写出该抛物线的顶点坐标,本题得以解决.
【解答】解:∵抛物线的解析式为y=﹣(x+2)2﹣3,
∴该抛物线的顶点坐标为(﹣2,﹣3),
故选:D.
4.(3分)在Rt△ABC中,∠C=90°,若AB=2,AC=1,则tanA的值为( )
A. B. C. D.
【分析】首先利用勾股定理计算出BC,再根据正切定义可得tanA=,代入线段长可得答案.
【解答】解:∵AB=2,AC=1,
∴CB==,
∴tanA==,
故选:D.
5.(3分)将抛物线y=2(x﹣3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )
A.y=2(x﹣6)2 B.y=2(x﹣6)2+4
C.y=2x2 D.y=2x2+4
【分析】根据“左加右减、上加下减”的原则进行解答即可.
【解答】解:将抛物线y=2(x﹣3)2+2向左平移3个单位长度所得抛物线解析式为:y=2(x﹣3+3)2+2,即y=2x2+2;
再向下平移2个单位为:y=2x2+2﹣2,即y=2x2.
故选:C.
6.(3分)斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是( )
A.500 sinα米 B.米 C.500 cosα米 D.米
【分析】根据题意画出图形,再利用坡角的正弦值即可求解.
【解答】解:如图,∠A=α,AE=500.
则EF=500sinα.
故选:A.
7.(3分)某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)=182
【分析】主要考查增长率问题,一般增长后的量=增长前的量×(1+增长率),如果该厂五、六月份平均每月的增长率为x,那么可以用x分别表示五、六月份的产量,然后根据题意可得出方程.
【解答】解:依题意得五、六月份的产量为50(1+x)、50(1+x)2,
∴50+50(1+x)+50(1+x)2=182.
故选:B.
8.(3分)在△ABC中,∠C=90°,tanA=,则sinA=( )
A. B. C. D.
【分析】根据正切函数的定义,勾股定理,可得AB的长,根据正弦函数的定义,可得答案.
【解答】解:tanA==,
设BC=x,AC=3x,勾股定理,得
AB==x,
sinA===,
故选:A.
9.(3分)如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
【分析】先根据矩形的性质得AD∥BC,CD∥AB,再根据平行线分线段成比例定理,由DE∥BC得到=,=,则可对B、C进行判断;由DF∥AB得=,则可对A进行判断;由于=,利用BC=AD,则可对D进行判断.
【解答】解:∵四边形ABCD为矩形,
∴AD∥BC,CD∥AB
∵DE∥BC,
∴=,=,所以B、选项结论正确,C选项错误;
∵DF∥AB,
∴=,所以A选项的结论正确;
=,
而BC=AD,
∴=,所以D选项的结论正确.
故选:C.
10.(3分)清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校.图中的折线表示清清的行程s(米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A.清清等公交车时间为3分钟
B.清清步行的速度是80米/分
C.公交车的速度是500米/分
D.清清全程的平均速度为290米/分
【分析】根据图象可以确定他离家6800m用了多长时间,等公交车时间是多少,他步行的时间和对应的路程,公交车运行的时间和对应的路程,然后确定各自的速度.
【解答】解:A、依题意在第5min开始等公交车,第8min结束,故他等公交车时间为3min,故选项正确;
B、依题意得他离家400m共用了5min,故步行的速度为80米/分,故选项正确;
C、他公交车(20﹣8)min走了(6400﹣400)km,故公交车的速度为6000÷12=500m/min,故选项正确.
D、全程6800米,共用时25min,全程速度为272m/min,故选项错误;
故选:D.
二、填空题(每小题3分,共30分)
11.(3分)在函数y=中,自变量x的取值范围是 x≠﹣2 .
【分析】根据分式有意义,分母不等于0列式计算即可得解.
【解答】解:由题意得,x+2≠0,
解得x≠﹣2.
故答案为:x≠﹣2.
12.(3分)二次函数的解析式为,则常数m的值为 3 .
【分析】直接利用二次函数的定义分析得出答案.
【解答】解:∵是关于x的二次函数,
∴m2﹣3m+2=2,且m≠0,
解得:m=3.
故答案为:3.
13.(3分)二次函数y=﹣2(x﹣4)2+8的最大值为 8 .
【分析】根据顶点式可得当x=4时,y取得最大值8.
【解答】解:∵y=﹣2(x﹣4)2+8,
∴当x=4时,y取得最大值8,
故答案为:8.
14.(3分)二次函数y=﹣x2+3x﹣2与x轴的交点坐标是 (1,0)、(2,0) .
【分析】令y=0,解关于x的一元二次方程即可.
【解答】解:令y=0,则﹣x2+3x﹣2=0,
解得:x1=1,x2=2,
∴次函数y=﹣x2+3x﹣2与x轴的交点坐标是(1,0)、(2,0).
故答案为:(1,0)、(2,0).
15.(3分)如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于点D,已知AD=,那么BC= .
【分析】证明△BCD∽△BAC,根据相似三角形的性质列出比例式,计算即可.
【解答】解:∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠CDB=90°,
∵∠B=∠B,
∴△BCD∽△BAC,
∴=,即=,
解得:BC=,
故答案为:.
16.(3分)汽车刹车后行驶的距离s(米)与行驶的时间t(秒)函数关系式是s=15t﹣6t2,汽车刹车后停下来前进了 米.
【分析】利用配方法求二次函数最值的方法解答即可.
【解答】解:∵s=15t﹣6t2=﹣6(t﹣)2+,
∴汽车刹车后到停下来前进了m.
故答案为:.
17.(3分)二次函数y=ax2+bx+c(0≤x≤3)的图象如图所示,则y的取值范围是 ﹣1≤y≤3 .
【分析】根据图象中的数据可以得到当0≤x≤3时,函数值y的取值范围.
【解答】解:由图象可知,
当0≤x≤3时,函数值y的取值范围﹣1≤y≤3.
故答案为:﹣1≤y≤3.
18.(3分)某商店老板将一件进价为800元的商品先提价50%,再打8折卖出,则卖出这件商品所获利润是 160 元.
【分析】利用:利润=售价﹣进价,直接代入求值即可.
【解答】解:卖出这件商品所获利润=800×(1+50%)×0.8﹣800=160元.
故本题答案为:160.
19.(3分)等腰△ABC中,AB=AC,AD⊥BC于点D,点E在直线AC上,2CE=AC,若AD=6,BE=5,则BC= 或 .
【分析】分点E在AC上、点E在AC的延长线上两种情况,根据三角形的重心的概念、平行线分线段成比例定理计算即可.
【解答】解:如图1,∵AB=AC,AD⊥BC,
∴BD=DC,
∵AC=2CE,
∴AE=EC,
∴点F是三角形的重心,
∴DF=AD=2,BF=BE=,
∴BD===,
∴BC=2BD=,
如图2,过点E作EH⊥BC于H,
则EH∥AD,
∴===,
∴EH=AD=3,CD=2CH,
在Rt△BHE中,(CD)2+32=52,
解得:CD=,
∴BC=2CD=.
综上所述:BC的长为或,
故答案为:或.
20.(3分)如图,在四边形ABCD中,∠ADC=∠ABC=90°,连接AC,BD,过点B作BE⊥AC,垂足为E,若∠BDC+∠DAB=90°,BE=4,CD=6,则BC= 2 .
【分析】取AC中点为O,连接DO、BO,作OG⊥AD于点G,由直角三角形的斜边中线等于斜边的一半得出OD=OB=AC,从而可得点A、B、C、D在以AC为直径的圆上,利用圆周角的关系定理及∠BDC+∠DAB=90°可得∠GOD=∠BOC;再证明△DGO≌△BEO(AAS),并由勾股定理求得AC的长;然后再证明△ABE∽△BCE,设CE=x,利用相似三角形的性质得比例式,解得x的值,则可得答案.
【解答】解:如图,取AC中点为O,连接DO、BO,作OG⊥AD于点G,
∵∠ADC=∠ABC=90°,
∴OD=OB=0.5AC,
∴点A、B、C、D在以AC为直径的圆上,
∵∠BDC+∠DAB=90°,,
∴∠BOD+∠BOC=180°,
∵∠BOD+∠DOG=180°,
∴∠GOD=∠BOC,
又∵OG⊥AD,AO=OD,
∴∠GOD=∠GOA,∠GOD=∠EOB,
又∵∠DGO=∠BEO=90°,
∴△DGO≌△BEO(AAS),
∴DG=BE=4,AD=2DG=8,
在Rt△ADC中,由勾股定理得:
AC==10,
∵∠AEB=∠BEC=∠ABC=90°,
∴∠ABE+∠CBE=90°,∠CBE+∠ECB=90°,
∴∠ABE=∠ECB,
∴△ABE∽△BCE,
∴,
设CE=x,则AE=10﹣x,BE=4,
∴,
∴16=(10﹣x)x,
解得x=2或x=8(舍去),
经检验x=2是原方程的解,
∴CE=2.
故答案为:2.
三、解答题(21~22题各7分,23题、24题各8分,25~27题各10分,共60分)
21.(7分)先化简,再求代数式的值,其中a=tan60°﹣6sin30°.
【分析】先根据分式混合运算的法则把原式进行化简,再求出a的值代入进行计算即可.
【解答】解:原式=﹣
=﹣
=,
∵a=tan60°﹣6sin30°=﹣6×=﹣3,
∴原式==.
22.(7分)如图,图1,图2,均为正方形网格,每个小正方形的面积均为1.在这个正方形网格中,各个小正方形的顶点叫做格点.请在下面的网格中按要求画图,使得每个图形的顶点均在格点上.
(1)画一个直角三角形,且三边之比为1:2:;
(2)画一个边长为整数的菱形,且面积等于24.
【分析】(1)画一个边长分别为,2,5的三角形即可.
(2)画一个对角线从分别为6,8的菱形即可.
【解答】解:(1)如图1中,△ABC即为所求(答案不唯一).
(2)如图2中,菱形ABCD即为所求.
23.(8分)商场销售一批衬衫,每天可售出20件,每件盈利40元,为了扩大销售,决定取适当的降价措施,经调查发现,如果一件衬衫每降价1元,每天可多售出2件.设每件衬衫降价x元,每天盈利y元.
(1)求出y与x之间的函数关系式;(不需写自变量的取值范围)
(2)求出每件衬衫降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
【分析】(1)根据每天盈利等于每件利润×销售件数得到y=(40﹣x)(20+2x),整理即可;
(2)把y=﹣2x2+60x+800配成顶点式得到y=﹣2(x﹣15)2+1250,然后根据二次函数的最值问题即可得到答案.
【解答】解:(1)由题意,得:
y=(40﹣x)(20+2x)
=﹣2x2+60x+800,
所以y与x之间的函数关系式为y=﹣2x2+60x+800;
(2)y=﹣2x2+60x+800
=﹣2(x﹣15)2+1250,
∵a=﹣2<0,
∴当x=15时,y有最大值,其最大值为1250,
所以每件降价15元时,商场每天的盈利达到最大,盈利最大是1250元.
24.(8分)如图1,正方形ABCD中,点E是边BC延长线上一点,连接DE,过点B作BF⊥DE,垂足为点F,BF与CD相交于点G.
(1)求证:△BCG≌△DCE;
(2)如图2,连接BD,若BE=4,DG=2,求tan∠DBG的值.
【分析】(1)只要证明∠CBG=∠CDE,即可用ASA证明△BCG≌△DCE.
(2)利用勾股定理分别在RT△DHG,RT△BHG中,求出BH,HG即可解决.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BCG=∠DCE=90°,BC=CD,
∵BF⊥DE,
∴∠DFG=∠BCG=90°,
∵∠BGC=∠DGF,
∴∠CBG=∠CDE.
在△BCG和△DCE中,
,
∴△BCG≌△DCE,
(2)解:∵△BCG≌△DCE,
∴CG=CE,
∵BE=BC+CE=4,DG=CD﹣CG=2,
∴BC=CD=3,CG=CE=,
在RT△BDC中,∵∠BCD=90°,
∴BD===6,
过点G作GH⊥BD垂足为H,
∵∠DHG=45°,∠DHG=90°,DG=2,
∴=,
∴DH=2,
∴GH=DH=2,
∵BD=BH﹣DH,
∴BH=6﹣2=4,
在RT△BHG中,∵∠BHG=90°,
∴tan∠DBG=,
∴tan∠DBG=.
25.(10分)疫情期间,某物业公司欲购进A、B两种型号的防护服,若购入A种防护服30套,B种防护服50套,需6600元,若购入A种防护服40套,B种防护服10套,需3700元.
(1)求购进A、B两种防护服的单价分别是多少元?
(2)若该公司准备用不多于12300元的金额购进这两种防护服共150套,求A种防护服至少要购进多少套?
【分析】(1)根据购入A种防护服30套,B种防护服50套,需6600元,若购入A种防护服40套,B种防护服10套,需3700元,可以列出相应的二元一次方程组,然后求解即可;
(2)根据公司准备用不多于12300元的金额购进这两种防护服共150套,可以列出相应的不等式,然后求解即可.
【解答】解:(1)设购进A、B两种防护服的单价分别是a元、b元,
由题意可得,
解得,
答:购进A、B两种防护服的单价分别是70元、90元;
(2)设购进A种防护服x套,则购进B种防护服(150﹣x)套,
由题意可得70x+90(150﹣x)≤12300,
解得x≥60,
答:A种防护服至少要购进60套.
26.(10分)在四边形ABCD中,∠BCD=45°,对角线AC与BD相交于点E,并且AC⊥AB,BD⊥CD,分别延长BA与CD相交于点F.
(1)如图1,当△BCF为锐角三角形时,求证:AD平分∠CAF;
(2)如图2,在(1)的条件下,求证:AC﹣AB=AD;
(3)如图3,在(1)的条件下,作∠BAC的平分线交BC于点G,连接DG交AC于点H,若DF=BG,AC=6,求EH的长.
【分析】(1)由题目条件可得,点A,B,C,D四点共圆,所以∠DAC=∠DBC=45°,又∠CAF=90°,所以∠CAD=∠DAF,即AD平分∠CAF;
(2)过点D作DP⊥DA∠AC于点P,结合(1)中条件可知△ADP是等腰直角三角形,所以AP=AD,再根据条件可证明∠ADB=∠PDC,所以∠△BAD≌△CPD(SAS),则AB=PC,即可;
(3)先证明△DFA∽△BGA,则DA=BA;设AB=x,则DA=x,可得6﹣x= x,解得x=2,求得AB=2,AD=2;过点D作DM⊥BF于点M,所以DM=AM=AD=2,BM=AB+AM=4,tan∠DBM==,BD=2,DF=BD=,FM=1,BF=5,DF=,BG=,因为AC∥DM,AM=AB,所以AE=DM=1,BE=BD=,CE=CA﹣AE=5,所以CE=BF,可证△CDE≌△BDF(SAS),所以DE=DF=,则BC=2;过点G作GN∥AC交BD于点N,可求得GN=,BN=,NE=,因为EH∥GN,所以,即=,解之即可.
【解答】解:(1)∵AC⊥AB,BD⊥CD,
∴∠CAB=∠CAF=∠BDC=∠BDF=90°,点A,B,C,D四点共圆,
∴∠DAC=∠DBC,
∵∠BCD=45°,
∴∠DBC=45°,
∴∠DAC=45°,
∴∠DAF=45°,即AD平分∠CAF;
(2)过点D作DP⊥DA∠AC于点P,
∴∠DAP=90°,
∵∠DAC=45°,
∴AD=DP,即△ADP是等腰直角三角形,
∴AP=AD,
∵∠DAP=∠ADB+∠BDP=90°,∠BDP+∠PDC=90°,
∴∠ADB=∠PDC,
又由(1)知△BDC是等腰直角三角形,
∴BD=CD,
∴△BAD≌△CPD(SAS),
∴AB=PC,
∴AC=AP+PC=AD+AB,即AC﹣AB=AD;
(3)由(2)得,∠FAD=45°,
∵CA⊥AB,
∴∠CAB=90°,
∵AG平分∠BAC,
∴∠BAG=45°,
∴∠ABG=∠FAD,
∴∠BGA=180°﹣∠BAG﹣∠ABC=135°﹣∠ABC,
∵∠BCD=45°,
∴∠F=180°﹣∠FBC﹣∠FCB=135°﹣∠ABC,
∴∠BGA=∠F,
∴△DFA∽△BGA,
∴DF:BG=DA:BA,
∵DF=BG,
∴DA=BA,
设AB=x,则DA=x,
由(2)的结论可知,6﹣x= x,解得x=2,
∴AB=2,AD=2,
过点D作DM⊥BF于点M,
∵∠DAF=45°,
∴DM=AM=AD=2,
∴BM=AB+AM=4,
∴tan∠DBM==,BD=2,
∴DF=BD=,FM=1,
∴BF=5,DF=,
∴BG=,
∵AC∥DM,AM=AB,
∴AE=DM=1,BE=BD=,
∴CE=CA﹣AE=5,
∴CE=BF,
由(2)得∠DCE=∠DBF,CD=BD,
∴△CDE≌△BDF(SAS),
∴DE=DF=,
∴BC=2,
过点G作GN∥AC交BD于点N,
∴===,
∴GN=,BN=,NE=,
∴DN=+=,
又∵EH∥GN,
∴,即=,
∴EH=.
27.(10分)在平面直角坐标系中,O为坐标原点,四边形OAEB为矩形,对角线AB的直线解析式为y=kx﹣6k,且S△AOB=18.
(1)如图1,求k的值;
(2)如图2,点P在线段AB上运动,其横坐标为t,连接OP,过点P作CP⊥OP,交BE于点C,设线段BC的长为d,求d与t之间的函数关系式;
(3)如图3,在(2)的条件下,延长OP交AE于点D(AD<DE),过点D作DQ∥x轴,交PC于点Q,若BC+AD=5,求线段DQ的长.
【分析】(1)根据函数解析式可得A、B的坐标,求得OA、OB的长度,再利用S△AOB=18,即可求出k的值;
(2)由点P在线段AB上运动,其横坐标为t,得出点P的横纵坐标,得出PN、ON、BM的长度,由△OPN≌△CPM得出CM=ON,再由BM=BC+CM,即可得出d与t之间的函数关系式;
(3)延长DA到F,使AF=BC,连接OF、OC、CD,先证明△OBC≌△OAF,得出∠BOC=∠AOF,OC=OF,再证明△COD≌△FOD,得出CD的长度,利用勾股定理求出AD的长度,进而求出DP、DO的长度,再利用△QPD∽△DAO,即可求出DQ的长.
【解答】解:(1)∵对角线AB的直线解析式为y=kx﹣6k,
∴当x=0时,y=﹣6k,当y=0时,x=6,
∴OA=6,OB=﹣6k,
∵S△AOB=OA OB=18,
∴×6×(﹣6k)=18,
∴k=﹣1;
(2)如图,过点P作PN⊥OB于点N,PM⊥BE于点M,则∠PMC=∠PNO=90°,
由(1)可得直线AB的解析式为:y=﹣x+6,
∵点P在线段AB上运动,其横坐标为t,
∴P(t,﹣t+6),B(0,6),
∴BM=PN=t,ON=﹣t+6,PM=BN=6﹣(﹣t+6)=t,
∴PM=PN,
∵PN⊥OB,PM⊥BE,
∴∠PMC=∠PNO=90°,
∵CP⊥OP,
∴∠OPN+∠NPC=∠NPC+∠CPM=90°,
∴∠OPN=∠CPM,
∴△OPN≌△CPM(ASA),
∴CM=ON=﹣t+6,
∵BM=BC+CM,BC=d,
∴t=d+(﹣t+6),
∴d=2t﹣6;
(3)延长DA到F,使AF=BC,连接OF、OC、CD,
∵OA=OB=6,∠OBC=∠OAF=90°,BC=AF,
∴△OBC≌△OAF(SAS),
∴∠BOC=∠AOF,OC=OF,
由(2)可知,△POC为等腰直角三角形,
∴∠POC=45°,
∴∠BOC+∠AOD=45°,
∴∠AOD+∠AOF=∠DOF=45°,
∴∠COD=∠FOD=45°,
∵OD=OD,
∴△COD≌△FOD(SAS),
∴CD=DF=DA+AF=DA+BC=5,
设AD=x,则AF=BC=5﹣x,CE=6﹣(5﹣x)=1+x,DE=6﹣x,
在Rt△CDE中,CE2+DE2=CD2,
∴(6﹣x)2+(1+x)2=52,
解得:x1=2,x2=3(舍去),
∴AD=2,
∴AF=BC=5﹣2=3,
∴OD===2,OC===3,
∴OP===,
∴DP=OD﹣OP=2﹣=,
∵DQ∥x轴,
∴∠QDP=∠DOA,
∵∠QPD=∠DAO=90°,
∴△QPD∽△DAO,
∴,
∴,
∴DQ=.
一、选择题(每小题3分共30分)
1.(3分)如果a与﹣2互为相反数,那么a等于( )
A.﹣2 B.2 C.﹣ D.
2.(3分)下列运算正确的是( )
A.a3 a2=a6 B.(x3)3=x6 C.x5+x5=x10 D.﹣a8÷a4=﹣a4
3.(3分)已知抛物线的解析式为y=﹣(x+2)2﹣3,则该抛物线的顶点坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
4.(3分)在Rt△ABC中,∠C=90°,若AB=2,AC=1,则tanA的值为( )
A. B. C. D.
5.(3分)将抛物线y=2(x﹣3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )
A.y=2(x﹣6)2 B.y=2(x﹣6)2+4
C.y=2x2 D.y=2x2+4
6.(3分)斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是( )
A.500 sinα米 B.米 C.500 cosα米 D.米
7.(3分)某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)=182
8.(3分)在△ABC中,∠C=90°,tanA=,则sinA=( )
A. B. C. D.
9.(3分)如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
10.(3分)清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校.图中的折线表示清清的行程s(米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A.清清等公交车时间为3分钟
B.清清步行的速度是80米/分
C.公交车的速度是500米/分
D.清清全程的平均速度为290米/分
二、填空题(每小题3分,共30分)
11.(3分)在函数y=中,自变量x的取值范围是 .
12.(3分)二次函数的解析式为,则常数m的值为 .
13.(3分)二次函数y=﹣2(x﹣4)2+8的最大值为 .
14.(3分)二次函数y=﹣x2+3x﹣2与x轴的交点坐标是 .
15.(3分)如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于点D,已知AD=,那么BC= .
16.(3分)汽车刹车后行驶的距离s(米)与行驶的时间t(秒)函数关系式是s=15t﹣6t2,汽车刹车后停下来前进了 米.
17.(3分)二次函数y=ax2+bx+c(0≤x≤3)的图象如图所示,则y的取值范围是 .
18.(3分)某商店老板将一件进价为800元的商品先提价50%,再打8折卖出,则卖出这件商品所获利润是 元.
19.(3分)等腰△ABC中,AB=AC,AD⊥BC于点D,点E在直线AC上,2CE=AC,若AD=6,BE=5,则BC= .
20.(3分)如图,在四边形ABCD中,∠ADC=∠ABC=90°,连接AC,BD,过点B作BE⊥AC,垂足为E,若∠BDC+∠DAB=90°,BE=4,CD=6,则BC= .
三、解答题(21~22题各7分,23题、24题各8分,25~27题各10分,共60分)
21.(7分)先化简,再求代数式的值,其中a=tan60°﹣6sin30°.
22.(7分)如图,图1,图2,均为正方形网格,每个小正方形的面积均为1.在这个正方形网格中,各个小正方形的顶点叫做格点.请在下面的网格中按要求画图,使得每个图形的顶点均在格点上.
(1)画一个直角三角形,且三边之比为1:2:;
(2)画一个边长为整数的菱形,且面积等于24.
23.(8分)商场销售一批衬衫,每天可售出20件,每件盈利40元,为了扩大销售,决定取适当的降价措施,经调查发现,如果一件衬衫每降价1元,每天可多售出2件.设每件衬衫降价x元,每天盈利y元.
(1)求出y与x之间的函数关系式;(不需写自变量的取值范围)
(2)求出每件衬衫降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
24.(8分)如图1,正方形ABCD中,点E是边BC延长线上一点,连接DE,过点B作BF⊥DE,垂足为点F,BF与CD相交于点G.
(1)求证:△BCG≌△DCE;
(2)如图2,连接BD,若BE=4,DG=2,求tan∠DBG的值.
25.(10分)疫情期间,某物业公司欲购进A、B两种型号的防护服,若购入A种防护服30套,B种防护服50套,需6600元,若购入A种防护服40套,B种防护服10套,需3700元.
(1)求购进A、B两种防护服的单价分别是多少元?
(2)若该公司准备用不多于12300元的金额购进这两种防护服共150套,求A种防护服至少要购进多少套?
26.(10分)在四边形ABCD中,∠BCD=45°,对角线AC与BD相交于点E,并且AC⊥AB,BD⊥CD,分别延长BA与CD相交于点F.
(1)如图1,当△BCF为锐角三角形时,求证:AD平分∠CAF;
(2)如图2,在(1)的条件下,求证:AC﹣AB=AD;
(3)如图3,在(1)的条件下,作∠BAC的平分线交BC于点G,连接DG交AC于点H,若DF=BG,AC=6,求EH的长.
27.(10分)在平面直角坐标系中,O为坐标原点,四边形OAEB为矩形,对角线AB的直线解析式为y=kx﹣6k,且S△AOB=18.
(1)如图1,求k的值;
(2)如图2,点P在线段AB上运动,其横坐标为t,连接OP,过点P作CP⊥OP,交BE于点C,设线段BC的长为d,求d与t之间的函数关系式;
(3)如图3,在(2)的条件下,延长OP交AE于点D(AD<DE),过点D作DQ∥x轴,交PC于点Q,若BC+AD=5,求线段DQ的长.
2021-2022学年黑龙江省哈尔滨市香坊区九年级(上)月考数学试卷(10月份)(五四学制)
参考答案与试题解析
一、选择题(每小题3分共30分)
1.(3分)如果a与﹣2互为相反数,那么a等于( )
A.﹣2 B.2 C.﹣ D.
【分析】一个数的相反数就是在这个数前面添上“﹣”号.
【解答】解:﹣2的相反数是2,那么a等于2.
故选:B.
2.(3分)下列运算正确的是( )
A.a3 a2=a6 B.(x3)3=x6 C.x5+x5=x10 D.﹣a8÷a4=﹣a4
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=a5,不符合题意;
B、原式=x9,不符合题意;
C、原式=2x5,不符合题意;
D、原式=﹣a4,符合题意,
故选:D.
3.(3分)已知抛物线的解析式为y=﹣(x+2)2﹣3,则该抛物线的顶点坐标是( )
A.(2,3) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
【分析】根据题目中的抛物线的解析式,可以直接写出该抛物线的顶点坐标,本题得以解决.
【解答】解:∵抛物线的解析式为y=﹣(x+2)2﹣3,
∴该抛物线的顶点坐标为(﹣2,﹣3),
故选:D.
4.(3分)在Rt△ABC中,∠C=90°,若AB=2,AC=1,则tanA的值为( )
A. B. C. D.
【分析】首先利用勾股定理计算出BC,再根据正切定义可得tanA=,代入线段长可得答案.
【解答】解:∵AB=2,AC=1,
∴CB==,
∴tanA==,
故选:D.
5.(3分)将抛物线y=2(x﹣3)2+2向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )
A.y=2(x﹣6)2 B.y=2(x﹣6)2+4
C.y=2x2 D.y=2x2+4
【分析】根据“左加右减、上加下减”的原则进行解答即可.
【解答】解:将抛物线y=2(x﹣3)2+2向左平移3个单位长度所得抛物线解析式为:y=2(x﹣3+3)2+2,即y=2x2+2;
再向下平移2个单位为:y=2x2+2﹣2,即y=2x2.
故选:C.
6.(3分)斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是( )
A.500 sinα米 B.米 C.500 cosα米 D.米
【分析】根据题意画出图形,再利用坡角的正弦值即可求解.
【解答】解:如图,∠A=α,AE=500.
则EF=500sinα.
故选:A.
7.(3分)某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)=182
【分析】主要考查增长率问题,一般增长后的量=增长前的量×(1+增长率),如果该厂五、六月份平均每月的增长率为x,那么可以用x分别表示五、六月份的产量,然后根据题意可得出方程.
【解答】解:依题意得五、六月份的产量为50(1+x)、50(1+x)2,
∴50+50(1+x)+50(1+x)2=182.
故选:B.
8.(3分)在△ABC中,∠C=90°,tanA=,则sinA=( )
A. B. C. D.
【分析】根据正切函数的定义,勾股定理,可得AB的长,根据正弦函数的定义,可得答案.
【解答】解:tanA==,
设BC=x,AC=3x,勾股定理,得
AB==x,
sinA===,
故选:A.
9.(3分)如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A. B. C. D.
【分析】先根据矩形的性质得AD∥BC,CD∥AB,再根据平行线分线段成比例定理,由DE∥BC得到=,=,则可对B、C进行判断;由DF∥AB得=,则可对A进行判断;由于=,利用BC=AD,则可对D进行判断.
【解答】解:∵四边形ABCD为矩形,
∴AD∥BC,CD∥AB
∵DE∥BC,
∴=,=,所以B、选项结论正确,C选项错误;
∵DF∥AB,
∴=,所以A选项的结论正确;
=,
而BC=AD,
∴=,所以D选项的结论正确.
故选:C.
10.(3分)清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校.图中的折线表示清清的行程s(米)与所花时间t(分)之间的函数关系.下列说法错误的是( )
A.清清等公交车时间为3分钟
B.清清步行的速度是80米/分
C.公交车的速度是500米/分
D.清清全程的平均速度为290米/分
【分析】根据图象可以确定他离家6800m用了多长时间,等公交车时间是多少,他步行的时间和对应的路程,公交车运行的时间和对应的路程,然后确定各自的速度.
【解答】解:A、依题意在第5min开始等公交车,第8min结束,故他等公交车时间为3min,故选项正确;
B、依题意得他离家400m共用了5min,故步行的速度为80米/分,故选项正确;
C、他公交车(20﹣8)min走了(6400﹣400)km,故公交车的速度为6000÷12=500m/min,故选项正确.
D、全程6800米,共用时25min,全程速度为272m/min,故选项错误;
故选:D.
二、填空题(每小题3分,共30分)
11.(3分)在函数y=中,自变量x的取值范围是 x≠﹣2 .
【分析】根据分式有意义,分母不等于0列式计算即可得解.
【解答】解:由题意得,x+2≠0,
解得x≠﹣2.
故答案为:x≠﹣2.
12.(3分)二次函数的解析式为,则常数m的值为 3 .
【分析】直接利用二次函数的定义分析得出答案.
【解答】解:∵是关于x的二次函数,
∴m2﹣3m+2=2,且m≠0,
解得:m=3.
故答案为:3.
13.(3分)二次函数y=﹣2(x﹣4)2+8的最大值为 8 .
【分析】根据顶点式可得当x=4时,y取得最大值8.
【解答】解:∵y=﹣2(x﹣4)2+8,
∴当x=4时,y取得最大值8,
故答案为:8.
14.(3分)二次函数y=﹣x2+3x﹣2与x轴的交点坐标是 (1,0)、(2,0) .
【分析】令y=0,解关于x的一元二次方程即可.
【解答】解:令y=0,则﹣x2+3x﹣2=0,
解得:x1=1,x2=2,
∴次函数y=﹣x2+3x﹣2与x轴的交点坐标是(1,0)、(2,0).
故答案为:(1,0)、(2,0).
15.(3分)如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于点D,已知AD=,那么BC= .
【分析】证明△BCD∽△BAC,根据相似三角形的性质列出比例式,计算即可.
【解答】解:∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠CDB=90°,
∵∠B=∠B,
∴△BCD∽△BAC,
∴=,即=,
解得:BC=,
故答案为:.
16.(3分)汽车刹车后行驶的距离s(米)与行驶的时间t(秒)函数关系式是s=15t﹣6t2,汽车刹车后停下来前进了 米.
【分析】利用配方法求二次函数最值的方法解答即可.
【解答】解:∵s=15t﹣6t2=﹣6(t﹣)2+,
∴汽车刹车后到停下来前进了m.
故答案为:.
17.(3分)二次函数y=ax2+bx+c(0≤x≤3)的图象如图所示,则y的取值范围是 ﹣1≤y≤3 .
【分析】根据图象中的数据可以得到当0≤x≤3时,函数值y的取值范围.
【解答】解:由图象可知,
当0≤x≤3时,函数值y的取值范围﹣1≤y≤3.
故答案为:﹣1≤y≤3.
18.(3分)某商店老板将一件进价为800元的商品先提价50%,再打8折卖出,则卖出这件商品所获利润是 160 元.
【分析】利用:利润=售价﹣进价,直接代入求值即可.
【解答】解:卖出这件商品所获利润=800×(1+50%)×0.8﹣800=160元.
故本题答案为:160.
19.(3分)等腰△ABC中,AB=AC,AD⊥BC于点D,点E在直线AC上,2CE=AC,若AD=6,BE=5,则BC= 或 .
【分析】分点E在AC上、点E在AC的延长线上两种情况,根据三角形的重心的概念、平行线分线段成比例定理计算即可.
【解答】解:如图1,∵AB=AC,AD⊥BC,
∴BD=DC,
∵AC=2CE,
∴AE=EC,
∴点F是三角形的重心,
∴DF=AD=2,BF=BE=,
∴BD===,
∴BC=2BD=,
如图2,过点E作EH⊥BC于H,
则EH∥AD,
∴===,
∴EH=AD=3,CD=2CH,
在Rt△BHE中,(CD)2+32=52,
解得:CD=,
∴BC=2CD=.
综上所述:BC的长为或,
故答案为:或.
20.(3分)如图,在四边形ABCD中,∠ADC=∠ABC=90°,连接AC,BD,过点B作BE⊥AC,垂足为E,若∠BDC+∠DAB=90°,BE=4,CD=6,则BC= 2 .
【分析】取AC中点为O,连接DO、BO,作OG⊥AD于点G,由直角三角形的斜边中线等于斜边的一半得出OD=OB=AC,从而可得点A、B、C、D在以AC为直径的圆上,利用圆周角的关系定理及∠BDC+∠DAB=90°可得∠GOD=∠BOC;再证明△DGO≌△BEO(AAS),并由勾股定理求得AC的长;然后再证明△ABE∽△BCE,设CE=x,利用相似三角形的性质得比例式,解得x的值,则可得答案.
【解答】解:如图,取AC中点为O,连接DO、BO,作OG⊥AD于点G,
∵∠ADC=∠ABC=90°,
∴OD=OB=0.5AC,
∴点A、B、C、D在以AC为直径的圆上,
∵∠BDC+∠DAB=90°,,
∴∠BOD+∠BOC=180°,
∵∠BOD+∠DOG=180°,
∴∠GOD=∠BOC,
又∵OG⊥AD,AO=OD,
∴∠GOD=∠GOA,∠GOD=∠EOB,
又∵∠DGO=∠BEO=90°,
∴△DGO≌△BEO(AAS),
∴DG=BE=4,AD=2DG=8,
在Rt△ADC中,由勾股定理得:
AC==10,
∵∠AEB=∠BEC=∠ABC=90°,
∴∠ABE+∠CBE=90°,∠CBE+∠ECB=90°,
∴∠ABE=∠ECB,
∴△ABE∽△BCE,
∴,
设CE=x,则AE=10﹣x,BE=4,
∴,
∴16=(10﹣x)x,
解得x=2或x=8(舍去),
经检验x=2是原方程的解,
∴CE=2.
故答案为:2.
三、解答题(21~22题各7分,23题、24题各8分,25~27题各10分,共60分)
21.(7分)先化简,再求代数式的值,其中a=tan60°﹣6sin30°.
【分析】先根据分式混合运算的法则把原式进行化简,再求出a的值代入进行计算即可.
【解答】解:原式=﹣
=﹣
=,
∵a=tan60°﹣6sin30°=﹣6×=﹣3,
∴原式==.
22.(7分)如图,图1,图2,均为正方形网格,每个小正方形的面积均为1.在这个正方形网格中,各个小正方形的顶点叫做格点.请在下面的网格中按要求画图,使得每个图形的顶点均在格点上.
(1)画一个直角三角形,且三边之比为1:2:;
(2)画一个边长为整数的菱形,且面积等于24.
【分析】(1)画一个边长分别为,2,5的三角形即可.
(2)画一个对角线从分别为6,8的菱形即可.
【解答】解:(1)如图1中,△ABC即为所求(答案不唯一).
(2)如图2中,菱形ABCD即为所求.
23.(8分)商场销售一批衬衫,每天可售出20件,每件盈利40元,为了扩大销售,决定取适当的降价措施,经调查发现,如果一件衬衫每降价1元,每天可多售出2件.设每件衬衫降价x元,每天盈利y元.
(1)求出y与x之间的函数关系式;(不需写自变量的取值范围)
(2)求出每件衬衫降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
【分析】(1)根据每天盈利等于每件利润×销售件数得到y=(40﹣x)(20+2x),整理即可;
(2)把y=﹣2x2+60x+800配成顶点式得到y=﹣2(x﹣15)2+1250,然后根据二次函数的最值问题即可得到答案.
【解答】解:(1)由题意,得:
y=(40﹣x)(20+2x)
=﹣2x2+60x+800,
所以y与x之间的函数关系式为y=﹣2x2+60x+800;
(2)y=﹣2x2+60x+800
=﹣2(x﹣15)2+1250,
∵a=﹣2<0,
∴当x=15时,y有最大值,其最大值为1250,
所以每件降价15元时,商场每天的盈利达到最大,盈利最大是1250元.
24.(8分)如图1,正方形ABCD中,点E是边BC延长线上一点,连接DE,过点B作BF⊥DE,垂足为点F,BF与CD相交于点G.
(1)求证:△BCG≌△DCE;
(2)如图2,连接BD,若BE=4,DG=2,求tan∠DBG的值.
【分析】(1)只要证明∠CBG=∠CDE,即可用ASA证明△BCG≌△DCE.
(2)利用勾股定理分别在RT△DHG,RT△BHG中,求出BH,HG即可解决.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BCG=∠DCE=90°,BC=CD,
∵BF⊥DE,
∴∠DFG=∠BCG=90°,
∵∠BGC=∠DGF,
∴∠CBG=∠CDE.
在△BCG和△DCE中,
,
∴△BCG≌△DCE,
(2)解:∵△BCG≌△DCE,
∴CG=CE,
∵BE=BC+CE=4,DG=CD﹣CG=2,
∴BC=CD=3,CG=CE=,
在RT△BDC中,∵∠BCD=90°,
∴BD===6,
过点G作GH⊥BD垂足为H,
∵∠DHG=45°,∠DHG=90°,DG=2,
∴=,
∴DH=2,
∴GH=DH=2,
∵BD=BH﹣DH,
∴BH=6﹣2=4,
在RT△BHG中,∵∠BHG=90°,
∴tan∠DBG=,
∴tan∠DBG=.
25.(10分)疫情期间,某物业公司欲购进A、B两种型号的防护服,若购入A种防护服30套,B种防护服50套,需6600元,若购入A种防护服40套,B种防护服10套,需3700元.
(1)求购进A、B两种防护服的单价分别是多少元?
(2)若该公司准备用不多于12300元的金额购进这两种防护服共150套,求A种防护服至少要购进多少套?
【分析】(1)根据购入A种防护服30套,B种防护服50套,需6600元,若购入A种防护服40套,B种防护服10套,需3700元,可以列出相应的二元一次方程组,然后求解即可;
(2)根据公司准备用不多于12300元的金额购进这两种防护服共150套,可以列出相应的不等式,然后求解即可.
【解答】解:(1)设购进A、B两种防护服的单价分别是a元、b元,
由题意可得,
解得,
答:购进A、B两种防护服的单价分别是70元、90元;
(2)设购进A种防护服x套,则购进B种防护服(150﹣x)套,
由题意可得70x+90(150﹣x)≤12300,
解得x≥60,
答:A种防护服至少要购进60套.
26.(10分)在四边形ABCD中,∠BCD=45°,对角线AC与BD相交于点E,并且AC⊥AB,BD⊥CD,分别延长BA与CD相交于点F.
(1)如图1,当△BCF为锐角三角形时,求证:AD平分∠CAF;
(2)如图2,在(1)的条件下,求证:AC﹣AB=AD;
(3)如图3,在(1)的条件下,作∠BAC的平分线交BC于点G,连接DG交AC于点H,若DF=BG,AC=6,求EH的长.
【分析】(1)由题目条件可得,点A,B,C,D四点共圆,所以∠DAC=∠DBC=45°,又∠CAF=90°,所以∠CAD=∠DAF,即AD平分∠CAF;
(2)过点D作DP⊥DA∠AC于点P,结合(1)中条件可知△ADP是等腰直角三角形,所以AP=AD,再根据条件可证明∠ADB=∠PDC,所以∠△BAD≌△CPD(SAS),则AB=PC,即可;
(3)先证明△DFA∽△BGA,则DA=BA;设AB=x,则DA=x,可得6﹣x= x,解得x=2,求得AB=2,AD=2;过点D作DM⊥BF于点M,所以DM=AM=AD=2,BM=AB+AM=4,tan∠DBM==,BD=2,DF=BD=,FM=1,BF=5,DF=,BG=,因为AC∥DM,AM=AB,所以AE=DM=1,BE=BD=,CE=CA﹣AE=5,所以CE=BF,可证△CDE≌△BDF(SAS),所以DE=DF=,则BC=2;过点G作GN∥AC交BD于点N,可求得GN=,BN=,NE=,因为EH∥GN,所以,即=,解之即可.
【解答】解:(1)∵AC⊥AB,BD⊥CD,
∴∠CAB=∠CAF=∠BDC=∠BDF=90°,点A,B,C,D四点共圆,
∴∠DAC=∠DBC,
∵∠BCD=45°,
∴∠DBC=45°,
∴∠DAC=45°,
∴∠DAF=45°,即AD平分∠CAF;
(2)过点D作DP⊥DA∠AC于点P,
∴∠DAP=90°,
∵∠DAC=45°,
∴AD=DP,即△ADP是等腰直角三角形,
∴AP=AD,
∵∠DAP=∠ADB+∠BDP=90°,∠BDP+∠PDC=90°,
∴∠ADB=∠PDC,
又由(1)知△BDC是等腰直角三角形,
∴BD=CD,
∴△BAD≌△CPD(SAS),
∴AB=PC,
∴AC=AP+PC=AD+AB,即AC﹣AB=AD;
(3)由(2)得,∠FAD=45°,
∵CA⊥AB,
∴∠CAB=90°,
∵AG平分∠BAC,
∴∠BAG=45°,
∴∠ABG=∠FAD,
∴∠BGA=180°﹣∠BAG﹣∠ABC=135°﹣∠ABC,
∵∠BCD=45°,
∴∠F=180°﹣∠FBC﹣∠FCB=135°﹣∠ABC,
∴∠BGA=∠F,
∴△DFA∽△BGA,
∴DF:BG=DA:BA,
∵DF=BG,
∴DA=BA,
设AB=x,则DA=x,
由(2)的结论可知,6﹣x= x,解得x=2,
∴AB=2,AD=2,
过点D作DM⊥BF于点M,
∵∠DAF=45°,
∴DM=AM=AD=2,
∴BM=AB+AM=4,
∴tan∠DBM==,BD=2,
∴DF=BD=,FM=1,
∴BF=5,DF=,
∴BG=,
∵AC∥DM,AM=AB,
∴AE=DM=1,BE=BD=,
∴CE=CA﹣AE=5,
∴CE=BF,
由(2)得∠DCE=∠DBF,CD=BD,
∴△CDE≌△BDF(SAS),
∴DE=DF=,
∴BC=2,
过点G作GN∥AC交BD于点N,
∴===,
∴GN=,BN=,NE=,
∴DN=+=,
又∵EH∥GN,
∴,即=,
∴EH=.
27.(10分)在平面直角坐标系中,O为坐标原点,四边形OAEB为矩形,对角线AB的直线解析式为y=kx﹣6k,且S△AOB=18.
(1)如图1,求k的值;
(2)如图2,点P在线段AB上运动,其横坐标为t,连接OP,过点P作CP⊥OP,交BE于点C,设线段BC的长为d,求d与t之间的函数关系式;
(3)如图3,在(2)的条件下,延长OP交AE于点D(AD<DE),过点D作DQ∥x轴,交PC于点Q,若BC+AD=5,求线段DQ的长.
【分析】(1)根据函数解析式可得A、B的坐标,求得OA、OB的长度,再利用S△AOB=18,即可求出k的值;
(2)由点P在线段AB上运动,其横坐标为t,得出点P的横纵坐标,得出PN、ON、BM的长度,由△OPN≌△CPM得出CM=ON,再由BM=BC+CM,即可得出d与t之间的函数关系式;
(3)延长DA到F,使AF=BC,连接OF、OC、CD,先证明△OBC≌△OAF,得出∠BOC=∠AOF,OC=OF,再证明△COD≌△FOD,得出CD的长度,利用勾股定理求出AD的长度,进而求出DP、DO的长度,再利用△QPD∽△DAO,即可求出DQ的长.
【解答】解:(1)∵对角线AB的直线解析式为y=kx﹣6k,
∴当x=0时,y=﹣6k,当y=0时,x=6,
∴OA=6,OB=﹣6k,
∵S△AOB=OA OB=18,
∴×6×(﹣6k)=18,
∴k=﹣1;
(2)如图,过点P作PN⊥OB于点N,PM⊥BE于点M,则∠PMC=∠PNO=90°,
由(1)可得直线AB的解析式为:y=﹣x+6,
∵点P在线段AB上运动,其横坐标为t,
∴P(t,﹣t+6),B(0,6),
∴BM=PN=t,ON=﹣t+6,PM=BN=6﹣(﹣t+6)=t,
∴PM=PN,
∵PN⊥OB,PM⊥BE,
∴∠PMC=∠PNO=90°,
∵CP⊥OP,
∴∠OPN+∠NPC=∠NPC+∠CPM=90°,
∴∠OPN=∠CPM,
∴△OPN≌△CPM(ASA),
∴CM=ON=﹣t+6,
∵BM=BC+CM,BC=d,
∴t=d+(﹣t+6),
∴d=2t﹣6;
(3)延长DA到F,使AF=BC,连接OF、OC、CD,
∵OA=OB=6,∠OBC=∠OAF=90°,BC=AF,
∴△OBC≌△OAF(SAS),
∴∠BOC=∠AOF,OC=OF,
由(2)可知,△POC为等腰直角三角形,
∴∠POC=45°,
∴∠BOC+∠AOD=45°,
∴∠AOD+∠AOF=∠DOF=45°,
∴∠COD=∠FOD=45°,
∵OD=OD,
∴△COD≌△FOD(SAS),
∴CD=DF=DA+AF=DA+BC=5,
设AD=x,则AF=BC=5﹣x,CE=6﹣(5﹣x)=1+x,DE=6﹣x,
在Rt△CDE中,CE2+DE2=CD2,
∴(6﹣x)2+(1+x)2=52,
解得:x1=2,x2=3(舍去),
∴AD=2,
∴AF=BC=5﹣2=3,
∴OD===2,OC===3,
∴OP===,
∴DP=OD﹣OP=2﹣=,
∵DQ∥x轴,
∴∠QDP=∠DOA,
∵∠QPD=∠DAO=90°,
∴△QPD∽△DAO,
∴,
∴,
∴DQ=.
同课章节目录
