2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.2.1 双曲线及其标准方程(共37张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.2.1 双曲线及其标准方程(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 12:21:30 | ||
图片预览











文档简介
(共37张PPT)
双曲线及其标准方程
F佳
定义 图 象
标准 方程
焦点
a,b,c的关系 |MF1|+|MF2|=2a(2a>|F1F2|)
x
y
o
F1
F2
·
·
·
M
y
o
x
F1
F2
·
M
·
a2=b2+c2
(-c,0), (c,0)
(0, -c) ,(0, c)
(a>b>0)
(a>b>0)
1.椭圆的定义
和
等于常数
2a ( 2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2. 引入问题:
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
|MF1|+|MF2|=2a( 2a>|F1F2|>0)
复习引入
探求轨迹
平面内到两个定点F1、F2的距离的差等于常数的动点的轨迹又是怎样的?
数学实验:
[1]取一条拉链;
[2]如图把它固定在
板上的两点F1、F2;
[3] 拉动拉链(M)。
思考:1、余下一段拉链的目的是什么?
2、谁是动点,谁是定点
3、给双曲线下定义
双曲线的形成过程
思考:1、余下一段拉链的目的是什么?
2、谁是动点,谁是定点
3、给双曲线下定义
探究双曲线的定义
①如图(A),
|MF1|-|MF2|=|F2F|=2a
②如图(B),
上面 两条合起来叫做双曲线
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
|MF2|-|MF1|=|F1F|=2a
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
o
F
2
F
1
M
平面内与两个定点F1、F2的距离的差的绝对值等于非零常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
双曲线定义
| |MF1| - |MF2| | = 2a
没有“绝对值”这个条件时,仅表示双曲线的一支.
③此常数记为2a,则a我们根据这个几何性质来得出双曲线的定义.
2
F
F
1
M
A
B
C
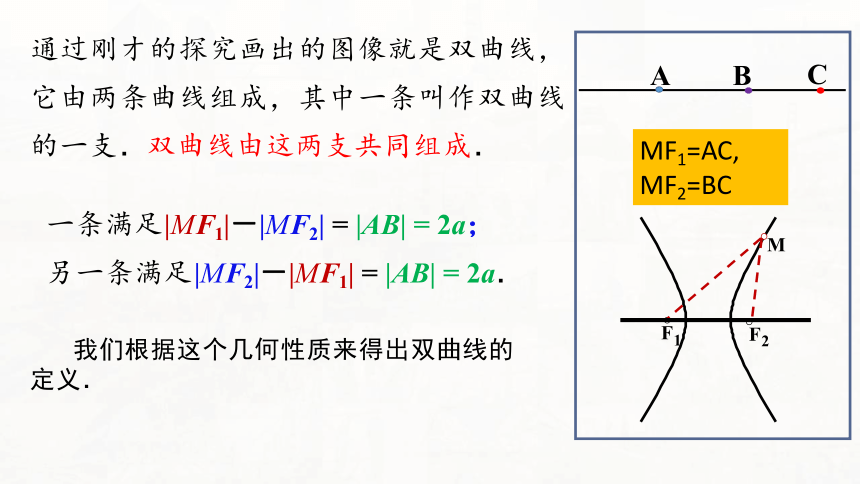
MF1=AC, MF2=BC
通过刚才的探究画出的图像就是双曲线,它由两条曲线组成,其中一条叫作双曲线的一支.双曲线由这两支共同组成.
一条满足|MF1|-|MF2| = |AB| = 2a;
另一条满足|MF2|-|MF1| = |AB| = 2a.
全优P104 右边 预习自测 1
1.思维辨析(对的画"√",错的画"×")
(1)在双曲线标准方程=1中,a>0,b>0且a≠b. ( )
(2)双曲线标准方程中,a,b的大小关系是a>b. ( )
课本P121 练习 4
4.双曲线=1(a>0)的两个焦点分别是F1与F2,焦距为8;M是双曲线上的一点,且|MF1|=5,求|MF2|的值.
作业:课本P127 习题3.2 1
(要写解题过程)
【动手操作,感悟新知】
问:类比椭圆,这个几何条件有没有限制条件?
2a
理解定义
对双曲线定义中的条件加以改变,则动点
M的轨迹是怎么样的呢?
例如:
(
1
)
0
2
=
a
;
(
2
)
c
a
2
2
=
;
(
3
)
c
a
2
2
>
||MF1|-|MF2||=|F1F2|时,M点一定在上图中的射线F1P,F2Q 上,此时点的轨迹为两条射线F1P、F2Q。
②常数大于|F1F2 |时
①常数等于|F1F2|时
|MF1|-|MF2| >|F1F2|
F2
F1
P
M
Q
M
是不可能的,因为三角形两边之差小于第三边。此时无轨迹。
此时点的轨迹是线段F1F2的垂直平分线。
则|MF1|=|MF2|
F1
F2
M
③常数等于0时
∵若常数2a= |MF1|-|MF2| =0
【概念剖析,学以致用】
概念辨析
判断下列点的轨迹是不是双曲线?
①平面内两定点距离为10,平面内到F 的距离与到F 距离差
为6的点的轨迹。
②平面内两定点距离为10,平面内到F 的距离与到F 距离差
的绝对值为12的点的轨迹。
③平面直角坐标系内两定点F (-5,0),F (5,0),平面内到F 的距离与到F 距离差的绝对值为6的点的轨迹。
×
×
√
1
2
1
1
1
2
2
2
【概念剖析,学以致用】
双
曲
线
定
义
两焦点间的距离叫做双曲线的焦距
两个定点 是焦点
全优P103 右边 预习自测
已知M(-3,0);N(3,0),|PM|-|PN|=6,则动点P的轨迹是( )
A.一条射线 B. 双曲线右支
C.双曲线 D.双曲线左支
生活中的双曲线
双曲线型自然通风冷却塔
法拉利主题公园
生活中的双曲线
双曲线在现实中的应用十分广泛,如:发电厂泠却塔的外形、广州塔的外形,通过声音时差测定位等都要用到双曲线。
[问题]:根据双曲线的定义如何用坐标法来探究双曲线的标准方程呢?
(一)建立平面直角坐标系
如图,取过焦点F1、 F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系.
设双曲线的焦距|F1F2|=2c,双曲线上的点与两定点的距离之差的绝对值为2a (a > 0),则F1、 F2的坐标分别为(-c,0),(c,0).
(二)设曲线上任意一点(或动点)的坐标为(x,y)
设M(x,y)为双曲线上任意一点.
x
O
y
F2
F1
M
(三)找出限制动点的几何条件
因为||MF1|-|MF2||=2a,即|MF1|-|MF2| = ±2a,
(四)将坐标代入几何关系
所以
(五)化简式子
由双曲线的定义知 2c>2a,即c>a,所以c -a >0.设c -a = b (b>0),
则 b x -a y = a2b ,
上式两边同时除以a2b ,得
这称为双曲线的标准方程,它所表示的双曲线焦点在x轴上.坐标分别为F1(-c,0),F2(c,0),c =a + b .而双曲线上的点到两焦点的距离之差的绝对值等于2a.
双曲线的标准方程
x
y
o
F1
F2
M
y
x
x
y
o
F1
F2
双曲线的标准方程:
=
x2
a2
-
y2
b2
1
(a>0,b>0)
方程
叫做双曲线的标准方程
它表示的双曲线焦点在x轴上,焦点为F1(-c,0),F2(c,0),且c2=a2+b2
M
y
x
x
y
o
F1
F2
M
y
x
x
y
o
F1
F2
M
y
x
x
y
o
F1
F2
M
y
x
y
x
y
x
F2
F1
M
y
x
o
y
x
y
x
F2
F1
M
y
o
x
y
x
=
x2
a2
-
y2
b2
1
(a>0,b>0)
x2
y2
方程
叫做双曲线的标准方程
它表示的双曲线焦点在y轴上,焦点为F1(0,-c),F2(0,c),且c2=a2+b2
双曲线的标准方程
焦点在坐标轴上,且关于原点对称的双曲线的标准方程为:
焦点在x轴上:
焦点在y轴上:
双曲线的标准方程的特点:
(1)左边是两个分式的平方差,方程用“-”号连接;右边是1;
(2)三个参数a、b、c满足 c =a + b , a、b大小不定;
(3)系数为正的项的分母是a ,系数为负的项的分母就是 b ;
(4)如果x 的系数是正的,则焦点在x轴上; 如果y 的系数是正的,则焦点在y轴上.
如果x2的系数是正时,那么焦点在x轴上
P
如果y2的系数是正时,那么焦点在y轴上
判断焦点在哪条坐标轴上:
椭圆看分母,
双曲线看正负。
例1 已知双曲线的两个焦点分别为F1(-4,0),F2(4,0),双曲线上任一点到两个焦点的距离之差的绝对值等于6,求该双曲线的标准方程.
解:由于双曲线的焦点在x轴上,故可设它的标准方程为
由双曲线的定义知2a = 6,所以a = 3.
又因为c = 4,所以 b = c -a = 16-9= 7.
因此,所求双曲线的标准方程为
求标准方程时,
先定向,后定量.
课本P121 练习 2
2.求证∶双曲线x -15y =15与椭圆的焦点相同.
课本P121 练习 3
3.已知方程=1表示双曲线,求m的取值范围.
课本P121 练习 1
1.求适合下列条件的双曲线的标准方程∶
(1)焦点在x轴上,a=4,b=3;
(2)焦点在x轴上,经过点(-,-),(,);
(3)焦点为(0,-6),(0,6),且经过点(2,-5).
全优P104 左边 题型1 例1
例1.(1)求经过点P(-,2),Q(,-2)且焦点在坐标轴上的双曲线的标准方程;
(2)求与双曲线有公共焦点,且过点(,)的双曲线的标准方程.
作业:课本P127 习题3.2 2
使A、B两点在x轴上,并且点O与线段AB的中点重合
解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.
例2已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
如图所示,建立直角坐标系
x
y
o
P
B
A
即 2a=680,a=340
因此炮弹爆炸点的轨迹方程为
设爆炸点P的坐标为(x,y),则
本小节结束
F佳
双曲线及其标准方程
F佳
定义 图 象
标准 方程
焦点
a,b,c的关系 |MF1|+|MF2|=2a(2a>|F1F2|)
x
y
o
F1
F2
·
·
·
M
y
o
x
F1
F2
·
M
·
a2=b2+c2
(-c,0), (c,0)
(0, -c) ,(0, c)
(a>b>0)
(a>b>0)
1.椭圆的定义
和
等于常数
2a ( 2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2. 引入问题:
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
|MF1|+|MF2|=2a( 2a>|F1F2|>0)
复习引入
探求轨迹
平面内到两个定点F1、F2的距离的差等于常数的动点的轨迹又是怎样的?
数学实验:
[1]取一条拉链;
[2]如图把它固定在
板上的两点F1、F2;
[3] 拉动拉链(M)。
思考:1、余下一段拉链的目的是什么?
2、谁是动点,谁是定点
3、给双曲线下定义
双曲线的形成过程
思考:1、余下一段拉链的目的是什么?
2、谁是动点,谁是定点
3、给双曲线下定义
探究双曲线的定义
①如图(A),
|MF1|-|MF2|=|F2F|=2a
②如图(B),
上面 两条合起来叫做双曲线
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
|MF2|-|MF1|=|F1F|=2a
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
o
F
2
F
1
M
平面内与两个定点F1、F2的距离的差的绝对值等于非零常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
双曲线定义
| |MF1| - |MF2| | = 2a
没有“绝对值”这个条件时,仅表示双曲线的一支.
③此常数记为2a,则a
2
F
F
1
M
A
B
C
MF1=AC, MF2=BC
通过刚才的探究画出的图像就是双曲线,它由两条曲线组成,其中一条叫作双曲线的一支.双曲线由这两支共同组成.
一条满足|MF1|-|MF2| = |AB| = 2a;
另一条满足|MF2|-|MF1| = |AB| = 2a.
全优P104 右边 预习自测 1
1.思维辨析(对的画"√",错的画"×")
(1)在双曲线标准方程=1中,a>0,b>0且a≠b. ( )
(2)双曲线标准方程中,a,b的大小关系是a>b. ( )
课本P121 练习 4
4.双曲线=1(a>0)的两个焦点分别是F1与F2,焦距为8;M是双曲线上的一点,且|MF1|=5,求|MF2|的值.
作业:课本P127 习题3.2 1
(要写解题过程)
【动手操作,感悟新知】
问:类比椭圆,这个几何条件有没有限制条件?
2a
理解定义
对双曲线定义中的条件加以改变,则动点
M的轨迹是怎么样的呢?
例如:
(
1
)
0
2
=
a
;
(
2
)
c
a
2
2
=
;
(
3
)
c
a
2
2
>
||MF1|-|MF2||=|F1F2|时,M点一定在上图中的射线F1P,F2Q 上,此时点的轨迹为两条射线F1P、F2Q。
②常数大于|F1F2 |时
①常数等于|F1F2|时
|MF1|-|MF2| >|F1F2|
F2
F1
P
M
Q
M
是不可能的,因为三角形两边之差小于第三边。此时无轨迹。
此时点的轨迹是线段F1F2的垂直平分线。
则|MF1|=|MF2|
F1
F2
M
③常数等于0时
∵若常数2a= |MF1|-|MF2| =0
【概念剖析,学以致用】
概念辨析
判断下列点的轨迹是不是双曲线?
①平面内两定点距离为10,平面内到F 的距离与到F 距离差
为6的点的轨迹。
②平面内两定点距离为10,平面内到F 的距离与到F 距离差
的绝对值为12的点的轨迹。
③平面直角坐标系内两定点F (-5,0),F (5,0),平面内到F 的距离与到F 距离差的绝对值为6的点的轨迹。
×
×
√
1
2
1
1
1
2
2
2
【概念剖析,学以致用】
双
曲
线
定
义
两焦点间的距离叫做双曲线的焦距
两个定点 是焦点
全优P103 右边 预习自测
已知M(-3,0);N(3,0),|PM|-|PN|=6,则动点P的轨迹是( )
A.一条射线 B. 双曲线右支
C.双曲线 D.双曲线左支
生活中的双曲线
双曲线型自然通风冷却塔
法拉利主题公园
生活中的双曲线
双曲线在现实中的应用十分广泛,如:发电厂泠却塔的外形、广州塔的外形,通过声音时差测定位等都要用到双曲线。
[问题]:根据双曲线的定义如何用坐标法来探究双曲线的标准方程呢?
(一)建立平面直角坐标系
如图,取过焦点F1、 F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系.
设双曲线的焦距|F1F2|=2c,双曲线上的点与两定点的距离之差的绝对值为2a (a > 0),则F1、 F2的坐标分别为(-c,0),(c,0).
(二)设曲线上任意一点(或动点)的坐标为(x,y)
设M(x,y)为双曲线上任意一点.
x
O
y
F2
F1
M
(三)找出限制动点的几何条件
因为||MF1|-|MF2||=2a,即|MF1|-|MF2| = ±2a,
(四)将坐标代入几何关系
所以
(五)化简式子
由双曲线的定义知 2c>2a,即c>a,所以c -a >0.设c -a = b (b>0),
则 b x -a y = a2b ,
上式两边同时除以a2b ,得
这称为双曲线的标准方程,它所表示的双曲线焦点在x轴上.坐标分别为F1(-c,0),F2(c,0),c =a + b .而双曲线上的点到两焦点的距离之差的绝对值等于2a.
双曲线的标准方程
x
y
o
F1
F2
M
y
x
x
y
o
F1
F2
双曲线的标准方程:
=
x2
a2
-
y2
b2
1
(a>0,b>0)
方程
叫做双曲线的标准方程
它表示的双曲线焦点在x轴上,焦点为F1(-c,0),F2(c,0),且c2=a2+b2
M
y
x
x
y
o
F1
F2
M
y
x
x
y
o
F1
F2
M
y
x
x
y
o
F1
F2
M
y
x
y
x
y
x
F2
F1
M
y
x
o
y
x
y
x
F2
F1
M
y
o
x
y
x
=
x2
a2
-
y2
b2
1
(a>0,b>0)
x2
y2
方程
叫做双曲线的标准方程
它表示的双曲线焦点在y轴上,焦点为F1(0,-c),F2(0,c),且c2=a2+b2
双曲线的标准方程
焦点在坐标轴上,且关于原点对称的双曲线的标准方程为:
焦点在x轴上:
焦点在y轴上:
双曲线的标准方程的特点:
(1)左边是两个分式的平方差,方程用“-”号连接;右边是1;
(2)三个参数a、b、c满足 c =a + b , a、b大小不定;
(3)系数为正的项的分母是a ,系数为负的项的分母就是 b ;
(4)如果x 的系数是正的,则焦点在x轴上; 如果y 的系数是正的,则焦点在y轴上.
如果x2的系数是正时,那么焦点在x轴上
P
如果y2的系数是正时,那么焦点在y轴上
判断焦点在哪条坐标轴上:
椭圆看分母,
双曲线看正负。
例1 已知双曲线的两个焦点分别为F1(-4,0),F2(4,0),双曲线上任一点到两个焦点的距离之差的绝对值等于6,求该双曲线的标准方程.
解:由于双曲线的焦点在x轴上,故可设它的标准方程为
由双曲线的定义知2a = 6,所以a = 3.
又因为c = 4,所以 b = c -a = 16-9= 7.
因此,所求双曲线的标准方程为
求标准方程时,
先定向,后定量.
课本P121 练习 2
2.求证∶双曲线x -15y =15与椭圆的焦点相同.
课本P121 练习 3
3.已知方程=1表示双曲线,求m的取值范围.
课本P121 练习 1
1.求适合下列条件的双曲线的标准方程∶
(1)焦点在x轴上,a=4,b=3;
(2)焦点在x轴上,经过点(-,-),(,);
(3)焦点为(0,-6),(0,6),且经过点(2,-5).
全优P104 左边 题型1 例1
例1.(1)求经过点P(-,2),Q(,-2)且焦点在坐标轴上的双曲线的标准方程;
(2)求与双曲线有公共焦点,且过点(,)的双曲线的标准方程.
作业:课本P127 习题3.2 2
使A、B两点在x轴上,并且点O与线段AB的中点重合
解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.
例2已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
如图所示,建立直角坐标系
x
y
o
P
B
A
即 2a=680,a=340
因此炮弹爆炸点的轨迹方程为
设爆炸点P的坐标为(x,y),则
本小节结束
F佳
