2021-2022学年高二上学期数学人教A版(2019)必修第一册4.4.2 对数函数的图象和其性质 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)必修第一册4.4.2 对数函数的图象和其性质 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 680.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 14:54:14 | ||
图片预览




文档简介
(共21张PPT)
4.4.2
对数函数的图象和性质
第1课时
一、回顾旧知
1.对数函数的定义
一般地,函数
叫做对数函数.其中x是自变量,定义域是
2.指数函数的图像与性质
二、学习目标
1.会用描点法画对数函数的图象;
2.掌握对数函数的性质;
3.能用对数函数的图象性质比较对数的大小.
4.核心素养:数学抽象、数学运算.
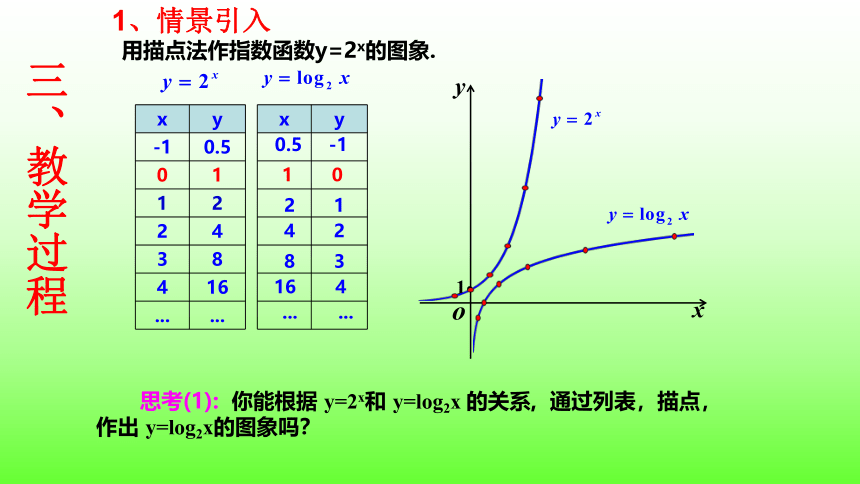
用描点法作指数函数y=2x的图象.
x y
-1 0.5
0 1
1 2
2 4
3 8
4 16
... ...
思考(1): 你能根据 y=2x和 y=log2x 的关系, 通过列表,描点,作出 y=log2x的图象吗?
x y
0.5
-1
1
0
2
1
4
2
8
3
16
4
...
...
三、教学过程
1、情景引入
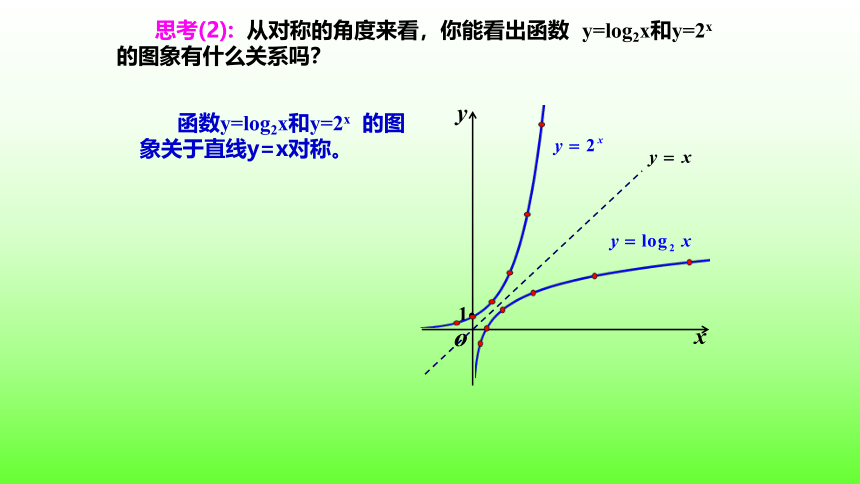
思考(2): 从对称的角度来看,你能看出函数 y=log2x和y=2x 的图象有什么关系吗?
函数y=log2x和y=2x 的图象关于直线y=x对称。
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
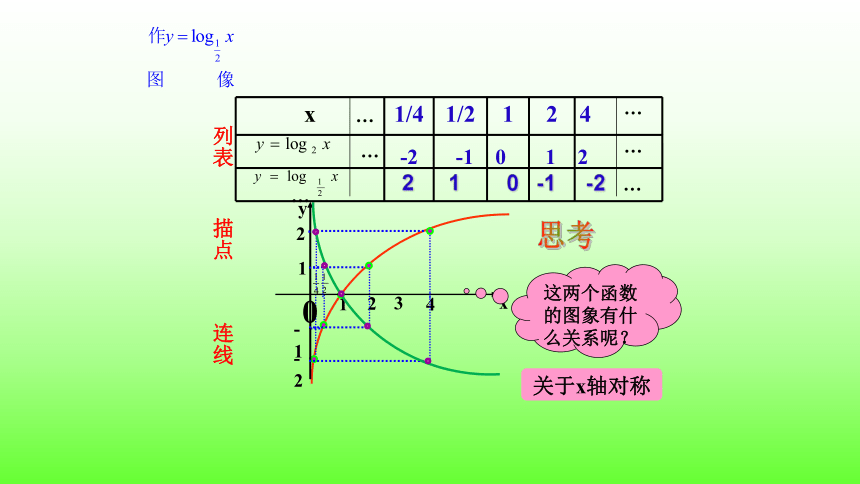
x 1/4 1/2 1 2 4
2 1 0 -1 -2
-2 -1 0 1 2
思考
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
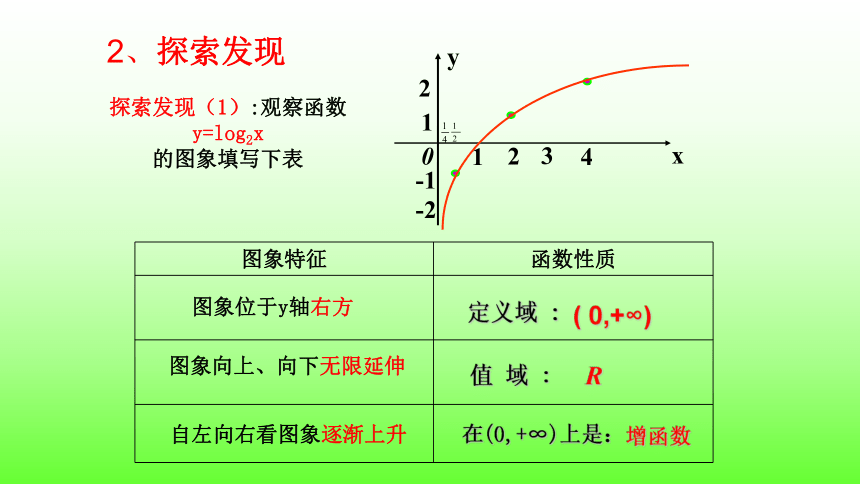
图象特征 函数性质
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现(1):观察函数y=log2x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
2
1
-1
-2
1
2
4
0
y
x
3
2、探索发现
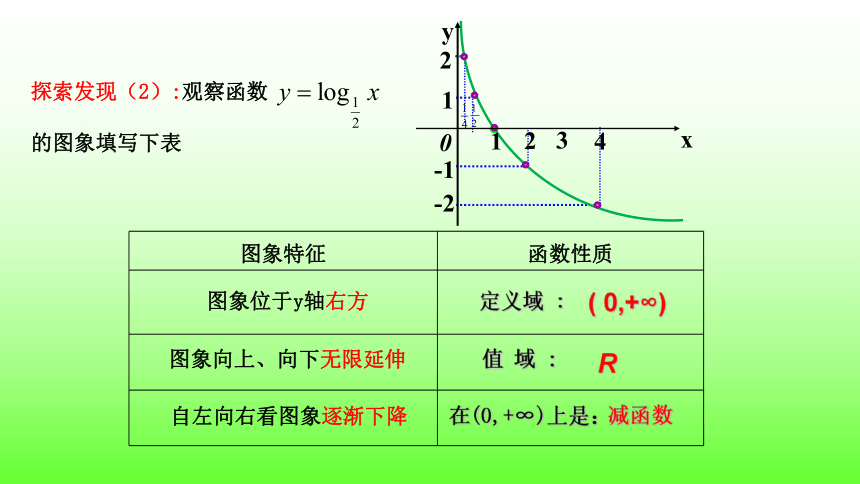
图象特征 函数性质
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
探索发现(2):观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
在同一个平面直角坐标系中画出对数函数 的图象
探索发现(3):
函数 y = log a x ( a>0 且 a≠1 ) 底数 a > 1 0 < a < 1
图象
定义域
值域
定点
值分布
单调性
趋势
对数函数的图象与性质:
1
x
y
o
1
x
y
o
( 0 , + ∞ )
R
R
( 0 , + ∞ )
( 1 , 0 )
( 1 , 0 )
当 x>1 时,y>0
当 0<x <1 时, y<0
当 x>1 时,y<0
当 0<x<1 时,y>0
在( 0 , + ∞ ) 上是增函数
在( 0 , + ∞ )上是减函数
底数越大,图象越靠近x轴
底数越小,图象越靠近x 轴
3、知识梳理
点睛
两个单调性相同的对数函数,它们的图象在位于直线x=1右侧的部分是“底大图低”,如图.
例1.比较下列各题中两个值的大小:
(1)log23.4, log28.5; (2) log 0.3 1.8, log 0.3 2.7;
(3)loga5.1, loga5.9.
解:
(1) ∵函数y=log 2 x的底数2大于1
∴y=log 2 x是增函数.
又∵3.4<8.5
∴ log23.4< log28.5
(2)∵函数y=log 0.3 x底数0.3<1
∴y=log 0.3 x 是减函数;
又∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7
四、例题分析
解: (3)当a>1时,
函数y=logax是增函数;
由5.1<5.9 得
∴ loga5.1 < loga5.9
当0函数y=logax是减函数;
由5.1<5.9得
loga5.1 > loga5.9
例1.比较下列各题中两个值的大小:
(1)log23.4, log28.5; (2) log 0.3 1.8, log 0.3 2.7;
(3)loga5.1, loga5.9.
你能口答吗?
变一变还能口答吗?
<
>
>
<
<
>
>
<
<
<
<
<
练一练
比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵log 3π , log 2 0.8 .
解: ⑴∵log67>log66=1
log76<log77=1
∴ log67>log76
⑵ ∵log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8
提示 : log aa=1
提示: log a1=0
变式:
解:
返回
由换底公式得
(3)
即log0.13>log0.23
思考:根据以上经验,请你说说如何比较比较两个同底对数值的大小
比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
思维升华
比较下列各组中两个值的大小:
(1)log31.9,log32;(2)log23,log0.32;
解 (1)因为y=log3x在(0,+∞)上是增函数,
所以log31.9(2)因为log23>log21=0,log0.32所以log23>log0.32.
五、课堂练习
六、课堂小结:
作业: 课本P135 练习 2题
1.对数函数的图象和性质;
2.比较两个对数值的大小.
4.4.2
对数函数的图象和性质
第1课时
一、回顾旧知
1.对数函数的定义
一般地,函数
叫做对数函数.其中x是自变量,定义域是
2.指数函数的图像与性质
二、学习目标
1.会用描点法画对数函数的图象;
2.掌握对数函数的性质;
3.能用对数函数的图象性质比较对数的大小.
4.核心素养:数学抽象、数学运算.
用描点法作指数函数y=2x的图象.
x y
-1 0.5
0 1
1 2
2 4
3 8
4 16
... ...
思考(1): 你能根据 y=2x和 y=log2x 的关系, 通过列表,描点,作出 y=log2x的图象吗?
x y
0.5
-1
1
0
2
1
4
2
8
3
16
4
...
...
三、教学过程
1、情景引入
思考(2): 从对称的角度来看,你能看出函数 y=log2x和y=2x 的图象有什么关系吗?
函数y=log2x和y=2x 的图象关于直线y=x对称。
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x 1/4 1/2 1 2 4
2 1 0 -1 -2
-2 -1 0 1 2
思考
这两个函数的图象有什么关系呢?
关于x轴对称
…
…
…
…
…
…
图象特征 函数性质
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现(1):观察函数y=log2x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
2
1
-1
-2
1
2
4
0
y
x
3
2、探索发现
图象特征 函数性质
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
探索发现(2):观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
在同一个平面直角坐标系中画出对数函数 的图象
探索发现(3):
函数 y = log a x ( a>0 且 a≠1 ) 底数 a > 1 0 < a < 1
图象
定义域
值域
定点
值分布
单调性
趋势
对数函数的图象与性质:
1
x
y
o
1
x
y
o
( 0 , + ∞ )
R
R
( 0 , + ∞ )
( 1 , 0 )
( 1 , 0 )
当 x>1 时,y>0
当 0<x <1 时, y<0
当 x>1 时,y<0
当 0<x<1 时,y>0
在( 0 , + ∞ ) 上是增函数
在( 0 , + ∞ )上是减函数
底数越大,图象越靠近x轴
底数越小,图象越靠近x 轴
3、知识梳理
点睛
两个单调性相同的对数函数,它们的图象在位于直线x=1右侧的部分是“底大图低”,如图.
例1.比较下列各题中两个值的大小:
(1)log23.4, log28.5; (2) log 0.3 1.8, log 0.3 2.7;
(3)loga5.1, loga5.9.
解:
(1) ∵函数y=log 2 x的底数2大于1
∴y=log 2 x是增函数.
又∵3.4<8.5
∴ log23.4< log28.5
(2)∵函数y=log 0.3 x底数0.3<1
∴y=log 0.3 x 是减函数;
又∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7
四、例题分析
解: (3)当a>1时,
函数y=logax是增函数;
由5.1<5.9 得
∴ loga5.1 < loga5.9
当0
由5.1<5.9得
loga5.1 > loga5.9
例1.比较下列各题中两个值的大小:
(1)log23.4, log28.5; (2) log 0.3 1.8, log 0.3 2.7;
(3)loga5.1, loga5.9.
你能口答吗?
变一变还能口答吗?
<
>
>
<
<
>
>
<
<
<
<
<
练一练
比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵log 3π , log 2 0.8 .
解: ⑴∵log67>log66=1
log76<log77=1
∴ log67>log76
⑵ ∵log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8
提示 : log aa=1
提示: log a1=0
变式:
解:
返回
由换底公式得
(3)
即log0.13>log0.23
思考:根据以上经验,请你说说如何比较比较两个同底对数值的大小
比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
思维升华
比较下列各组中两个值的大小:
(1)log31.9,log32;(2)log23,log0.32;
解 (1)因为y=log3x在(0,+∞)上是增函数,
所以log31.9
五、课堂练习
六、课堂小结:
作业: 课本P135 练习 2题
1.对数函数的图象和性质;
2.比较两个对数值的大小.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
