2021——2022学年人教版八年级数学下册17.1.1勾股定理及拼图验证练习题(word版含答案)
文档属性
| 名称 | 2021——2022学年人教版八年级数学下册17.1.1勾股定理及拼图验证练习题(word版含答案) | 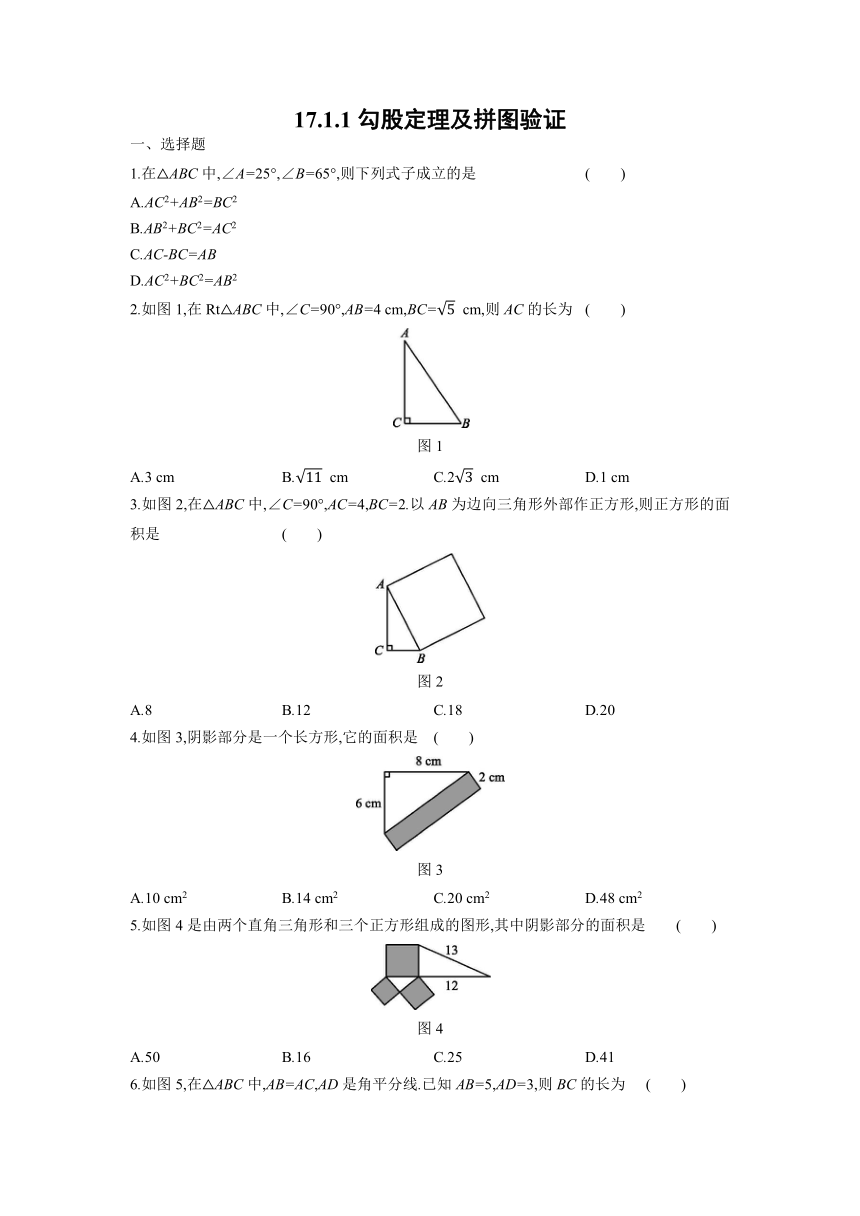 | |
| 格式 | docx | ||
| 文件大小 | 143.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 06:27:54 | ||
图片预览

文档简介
17.1.1勾股定理及拼图验证
一、选择题
1.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是 ( )
A.AC2+AB2=BC2
B.AB2+BC2=AC2
C.AC-BC=AB
D.AC2+BC2=AB2
2.如图1,在Rt△ABC中,∠C=90°,AB=4 cm,BC= cm,则AC的长为 ( )
图1
A.3 cm B. cm C.2 cm D.1 cm
3.如图2,在△ABC中,∠C=90°,AC=4,BC=2.以AB为边向三角形外部作正方形,则正方形的面积是 ( )
图2
A.8 B.12 C.18 D.20
4.如图3,阴影部分是一个长方形,它的面积是 ( )
图3
A.10 cm2 B.14 cm2 C.20 cm2 D.48 cm2
5.如图4是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是 ( )
图4
A.50 B.16 C.25 D.41
6.如图5,在△ABC中,AB=AC,AD是角平分线.已知AB=5,AD=3,则BC的长为 ( )
图5
A.5 B.6 C.8 D.10
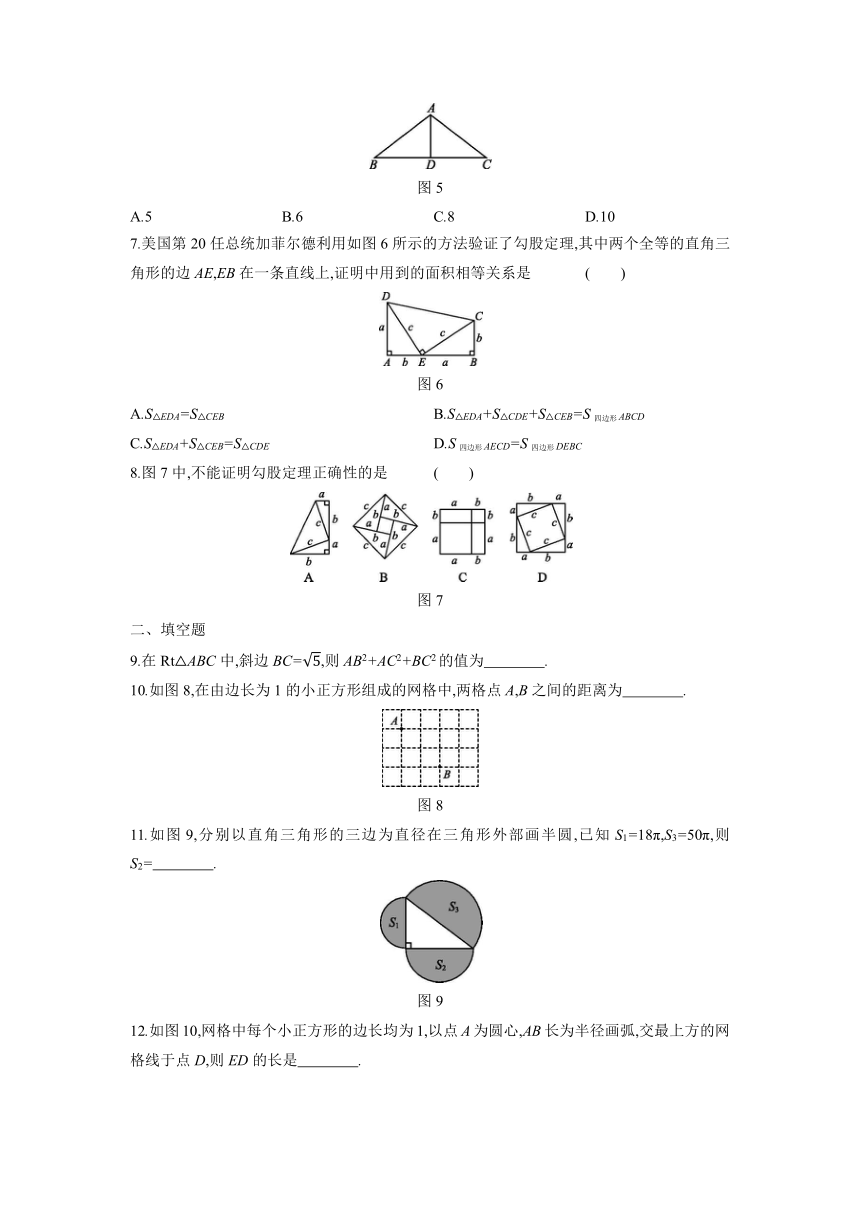
7.美国第20任总统加菲尔德利用如图6所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是 ( )
图6
A.S△EDA=S△CEB B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE D.S四边形AECD=S四边形DEBC
8.图7中,不能证明勾股定理正确性的是 ( )
图7
二、填空题
9.在Rt△ABC中,斜边BC=,则AB2+AC2+BC2的值为 .
10.如图8,在由边长为1的小正方形组成的网格中,两格点A,B之间的距离为 .
图8
11.如图9,分别以直角三角形的三边为直径在三角形外部画半圆,已知S1=18π,S3=50π,则S2= .
图9
12.如图10,网格中每个小正方形的边长均为1,以点A为圆心,AB长为半径画弧,交最上方的网格线于点D,则ED的长是 .
图10
三、解答题
13.在△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1)已知a=7,b=24,求c;
(2)已知a=4,c=7,求b.
14.用4个直角边长分别为a和b,斜边长为c的直角三角形和1个边长为c的正方形拼成如图11甲所示的边长为(a+b)的正方形,再用4个直角边长分别为a和b,斜边长为c的直角三角形和2个边长分别为a和b的正方形拼成如图乙所示的边长为(a+b)的正方形,试根据这两个图形验证勾股定理.
图11
15.在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图12①,则有a2+b2=c2.
若△ABC为锐角三角形,小明猜想:a2+b2>c2.理由如下:
如图②,过点A作AD⊥BC于点D.
设CD=x,则DB=a-x.
在Rt△ADC中,AD2=b2-x2;
在Rt△ADB中,AD2=c2-(a-x)2,
∴b2-x2=c2-(a-x)2,
化简,得a2+b2=c2+2ax.
∵a>0,x>0,
∴2ax>0,
∴a2+b2>c2,
∴若△ABC为锐角三角形,则a2+b2>c2.
(1)请你猜想:若△ABC为钝角三角形(∠C>90°),如图③,a2+b2与c2的大小关系;
(2)证明(1)中你的猜想.
图12
答案
1.D 2.B 3.D 4.C 5.A
6.C [解析] ∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,BD=CD.
∵AB=5,AD=3,
∴BD==4,
∴BC=2BD=8.故选C.
7.B 8.C 9.10 10.2
11.32π 12.
13.解:(1)由勾股定理,得a2+b2=c2,
所以c===25.
(2) 由勾股定理,得a2+b2=c2,
所以b===.
14.解:在图甲中,大正方形的面积为ab×4+c2=2ab+c2,
在图乙中,大正方形的面积为ab×4+a2+b2=2ab+a2+b2.
由题意知图甲中大正方形的面积与图乙中大正方形的面积相等,
所以2ab+c2=2ab+a2+b2,
即a2+b2=c2.
15.解:(1)猜想:若△ABC为钝角三角形(∠C>90°),则a2+b2与c2的大小关系为a2+b2(2)证明:如图,过点A作AH⊥BC交BC的延长线于点H.
设CH=y,则HB=a+y.
在Rt△AHC中,AH2=b2-y2;
在Rt△AHB中,AH2=c2-(a+y)2,
∴b2-y2=c2-(a+y)2,
化简,得a2+b2=c2-2ay.
∵a>0,y>0,
∴2ay>0,
∴a2+b2∴若△ABC为钝角三角形(∠C>90°),则a2+b2
一、选择题
1.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是 ( )
A.AC2+AB2=BC2
B.AB2+BC2=AC2
C.AC-BC=AB
D.AC2+BC2=AB2
2.如图1,在Rt△ABC中,∠C=90°,AB=4 cm,BC= cm,则AC的长为 ( )
图1
A.3 cm B. cm C.2 cm D.1 cm
3.如图2,在△ABC中,∠C=90°,AC=4,BC=2.以AB为边向三角形外部作正方形,则正方形的面积是 ( )
图2
A.8 B.12 C.18 D.20
4.如图3,阴影部分是一个长方形,它的面积是 ( )
图3
A.10 cm2 B.14 cm2 C.20 cm2 D.48 cm2
5.如图4是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是 ( )
图4
A.50 B.16 C.25 D.41
6.如图5,在△ABC中,AB=AC,AD是角平分线.已知AB=5,AD=3,则BC的长为 ( )
图5
A.5 B.6 C.8 D.10
7.美国第20任总统加菲尔德利用如图6所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是 ( )
图6
A.S△EDA=S△CEB B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE D.S四边形AECD=S四边形DEBC
8.图7中,不能证明勾股定理正确性的是 ( )
图7
二、填空题
9.在Rt△ABC中,斜边BC=,则AB2+AC2+BC2的值为 .
10.如图8,在由边长为1的小正方形组成的网格中,两格点A,B之间的距离为 .
图8
11.如图9,分别以直角三角形的三边为直径在三角形外部画半圆,已知S1=18π,S3=50π,则S2= .
图9
12.如图10,网格中每个小正方形的边长均为1,以点A为圆心,AB长为半径画弧,交最上方的网格线于点D,则ED的长是 .
图10
三、解答题
13.在△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1)已知a=7,b=24,求c;
(2)已知a=4,c=7,求b.
14.用4个直角边长分别为a和b,斜边长为c的直角三角形和1个边长为c的正方形拼成如图11甲所示的边长为(a+b)的正方形,再用4个直角边长分别为a和b,斜边长为c的直角三角形和2个边长分别为a和b的正方形拼成如图乙所示的边长为(a+b)的正方形,试根据这两个图形验证勾股定理.
图11
15.在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图12①,则有a2+b2=c2.
若△ABC为锐角三角形,小明猜想:a2+b2>c2.理由如下:
如图②,过点A作AD⊥BC于点D.
设CD=x,则DB=a-x.
在Rt△ADC中,AD2=b2-x2;
在Rt△ADB中,AD2=c2-(a-x)2,
∴b2-x2=c2-(a-x)2,
化简,得a2+b2=c2+2ax.
∵a>0,x>0,
∴2ax>0,
∴a2+b2>c2,
∴若△ABC为锐角三角形,则a2+b2>c2.
(1)请你猜想:若△ABC为钝角三角形(∠C>90°),如图③,a2+b2与c2的大小关系;
(2)证明(1)中你的猜想.
图12
答案
1.D 2.B 3.D 4.C 5.A
6.C [解析] ∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,BD=CD.
∵AB=5,AD=3,
∴BD==4,
∴BC=2BD=8.故选C.
7.B 8.C 9.10 10.2
11.32π 12.
13.解:(1)由勾股定理,得a2+b2=c2,
所以c===25.
(2) 由勾股定理,得a2+b2=c2,
所以b===.
14.解:在图甲中,大正方形的面积为ab×4+c2=2ab+c2,
在图乙中,大正方形的面积为ab×4+a2+b2=2ab+a2+b2.
由题意知图甲中大正方形的面积与图乙中大正方形的面积相等,
所以2ab+c2=2ab+a2+b2,
即a2+b2=c2.
15.解:(1)猜想:若△ABC为钝角三角形(∠C>90°),则a2+b2与c2的大小关系为a2+b2
设CH=y,则HB=a+y.
在Rt△AHC中,AH2=b2-y2;
在Rt△AHB中,AH2=c2-(a+y)2,
∴b2-y2=c2-(a+y)2,
化简,得a2+b2=c2-2ay.
∵a>0,y>0,
∴2ay>0,
∴a2+b2
