2021-2022学年冀教版八年级数学上册17.3勾股定理 同步练习题(word解析版)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册17.3勾股定理 同步练习题(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 337.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 06:44:52 | ||
图片预览




文档简介
2021-2022学年冀教版八年级数学上册《17.3勾股定理》同步练习题(附答案)
1.如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标介于( )
A.0和1之间 B.1和2之间 C.2和3之间 D.3和4之间
2.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
A.3 B.5 C.6 D.4
3.汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值是( )
A. B. C.3 D.
4.如图是我国古代数学家赵爽为了证明勾股定理,而构造的一个几何图形,称为赵爽弦图,如果在赵爽弦图的直角三角形中,有一个锐角是30°,则图中阴影部分的面积与大正方形面积的比是( )
A. B. C.﹣ D.
5.如图,一棵大树在离地面9米高的B处断裂,树顶A落在离树底BC的12米处,则大树断裂之前的高度为( )
A.9米 B.15米 C.21米 D.24米
6.如图,将一边长为a的正方形(最中间的小正方形)与四块边长为b的正方形(其中b>a)拼接在一起,则四边形ABCD的面积为( )
A.b2+(b﹣a)2 B.b2+a2 C.(b+a)2 D.a2+2ab
7.如图,△ABC的边BC在数轴上,AB⊥BC,且BC=3,AB=1,以C为圆心,AC长为半径画圆分别交数轴于点A′、点A″,那么数轴上点A′、点A″所表示的数分别是 、 .
8.如图,已知直角△ABC的两直角边分别为6,8,分别以其三边为直径作半圆,则图中阴影部分的面积为 .
9.如图,有赵爽弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=27,S3=1,则S1的值是 .
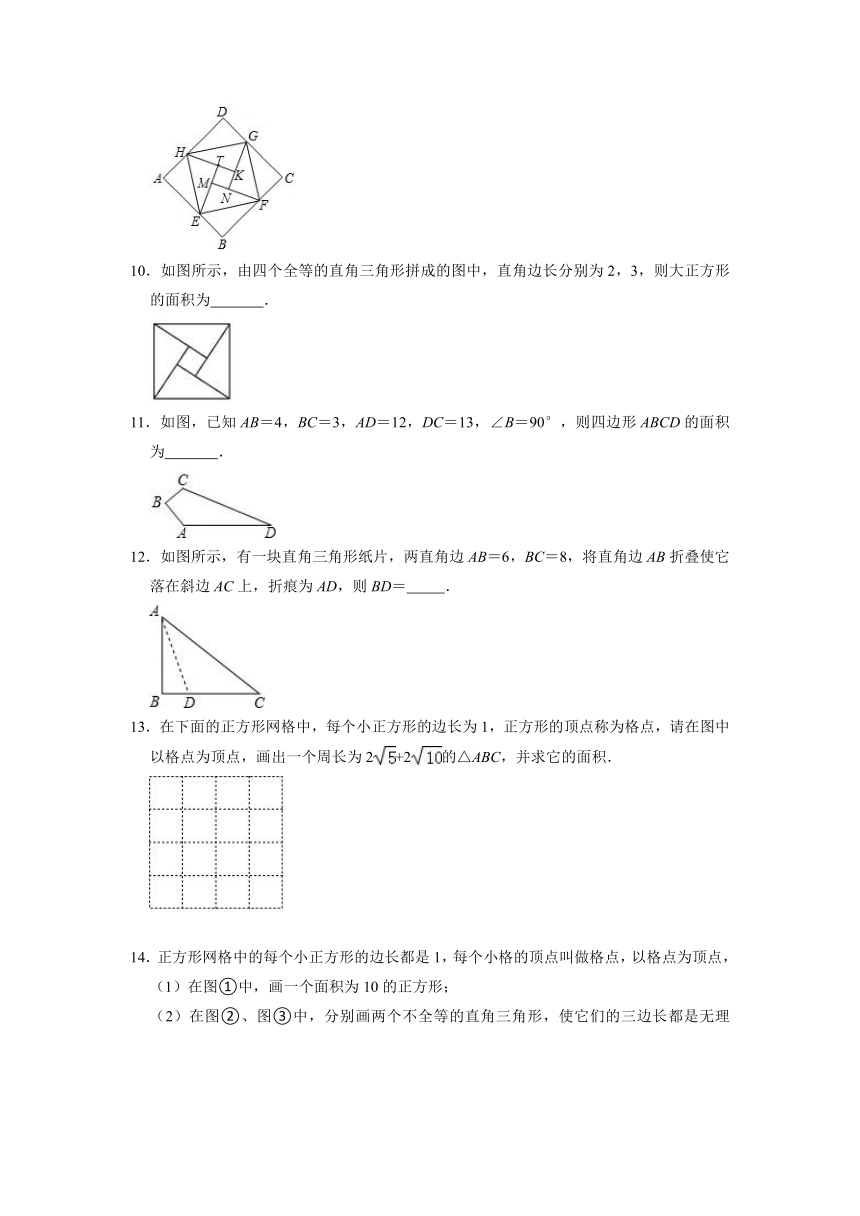
10.如图所示,由四个全等的直角三角形拼成的图中,直角边长分别为2,3,则大正方形的面积为 .
11.如图,已知AB=4,BC=3,AD=12,DC=13,∠B=90°,则四边形ABCD的面积为 .
12.如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将直角边AB折叠使它落在斜边AC上,折痕为AD,则BD= .
13.在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个周长为2+2的△ABC,并求它的面积.
14.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,
(1)在图①中,画一个面积为10的正方形;
(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.
15.如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
16.如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长;
(3)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
①请在x轴、y轴上找一点C,使△ABC为等腰三角形;(要求:用尺规画出所有符合条件的点,并用C1,C2,…, n在图中标出所找的点.只保留作图痕迹,不写作法)
②写出一个满足条件的在x轴上的点的坐标: ,写出一个满足条件的在y轴上的点坐标: .
17.如图的图形取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,试求(a+b)2的值.
18.观察、思考与验证
(1)如图1是一个重要公式的几何解释,请你写出这个公式 ;
(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°;
(3)伽菲尔德(任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在《新英格兰教育日志》上),请你写出验证过程.
19.如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
20.张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22﹣1 32﹣1 42﹣1 52﹣1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a= ,b= ,c= ;
(2)猜想:以a,b,c为边的三角形是否为直角三角形并证明你的猜想.
21.阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
22.观察下表
列 举 猜 想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
… …
13、b、c 132=b+c
请你结合该表格及相关知识,求出b,c的值,并验证13,b,c是否是勾股数?
参考答案
1.解:∵点A,B的坐标分别为(﹣2,0),(0,3),
∴OA=2,OB=3,
在Rt△AOB中,由勾股定理得:AB==,
∴AC=AB=,
∴OC=﹣2,
∴点C的坐标为(﹣2,0),
∵,
∴,
即点C的横坐标介于1和2之间,
故选:B.
2.解:由勾股定理得:AB==5;
故选:B.
3.解:将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=10,
∴得出S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=10,故3x+12y=10,
x+4y=,
所以S2=x+4y=,
故选:B.
4.解:设阴影部分的面积为s,直角三角形的两直角边分别是a、b,
∴小正方形的边长为,即b﹣a=,
∵直角三角形中较小的锐角为30°,
∴b=a,
解得:a=,b=,
∵大正方形的面积=c2=a2+b2,
∴大正方形的面积=()2+()2=(4+2)s.
∴阴影部分的面积与大正方形面积的比是:.
故选:D.
5.解:由题意得BC=9,在直角三角形ABC中,根据勾股定理得:AB=15米.
所以大树的高度是15+9=24米.
故选:D.
6.解:∵DE=b﹣a,AE=b,
∴S四边形ABCD=4S△ADE+a2=4××(b﹣a) b+a2
=b2+(b﹣a)2.
故选:A.
7.解:由勾股定理得,AC==,
则CA′=CA′′=,
∴OA′=﹣1,OA′′=+1,
∴A′、点A″所表示的数分别是1﹣和1+
故答案为:1﹣;1+.
8.解:在Rt△ABC中,AC=6,BC=8,
根据勾股定理得:AB==10,
则S阴影=S半圆AC+S半圆BC+S△ABC﹣S半圆AB=π+π+×6×8﹣π=24.
故答案为:24
9.解:∵八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,
∴CG=NG,CF=DG=NF,
∴S1=(CG+DG)2
=CG2+DG2+2CG DG
=GF2+2CG DG,
S2=GF2,
S3=(NG﹣NF)2=NG2+NF2﹣2NG NF,
∴S1+S2+S3=GF2+2CG DG+GF2+NG2+NF2﹣2NG NF=3GF2=27,
∴GF2=9,
∴S2=9,
∵S3=1,
∴S1的值是17.
故答案为17.
10.解:∵直角三角形的两条直角边长分别为2,3,
∴整个大正方形的边长为:=,
∴整个大正方形的面积为:13.
11.解:连接AC,
∵∠B=90°
∴AC2=AB2+BC2=16+9=25
∵AD2=144,DC2=169
∴AC2+AD2=DC2
∴CA⊥AD
∴S四ABCD=S△ABC+S△ACD=34+×125=36.
12.解:设点B落在AC上的E点处,连接DE,如图所示,
∵△ABC为直角三角形,AB=6,BC=8,
∴根据勾股定理得:AC==10,
设BD=x,由折叠可知:DE=BD=x,AE=AB=6,
可得:CE=AC﹣AE=10﹣6=4,CD=BC﹣BD=8﹣x,
在Rt△CDE中,
根据勾股定理得:(8﹣x)2=42+x2,
解得:x=3,
则BD=3.
故答案为:3.
13.解:△ABC是一个周长为2+2三角形,
△ABC的面积=3×4﹣×2×4﹣×1×3﹣×1×3=5.
14.解:(1)如图①所示:
(2)如图②③所示.
15.解:(1)∵BQ=2×2=4(cm),BP=AB﹣AP=16﹣2×1=14(cm ),∠B=90°,
∴PQ===(cm);
(2)BQ=2t,BP=16﹣t,
根据题意得:2t=16﹣t,
解得:t=,
即出发秒钟后,△PQB能形成等腰三角形;
(3)①当CQ=BQ时,如图1所示,
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.
③当BC=BQ时,如图3所示,
过B点作BE⊥AC于点E,
则BE==,
∴CE=,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
16.解:(1)由图可得,×(a+b)(a+b)=ab+c2+ab,
整理得,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
(2)当a=2,b=4时,
可得:c=;
如图1:
所以四边形的周长为:8+4;
(3)如图2:
一个满足条件的在x轴上的点的坐标:(﹣1,0);
一个满足条件的在y轴上的点的坐标:(0,2+).
故答案为:(﹣1,0);(0,2+),
17.解:∵大正方形的面积是13,小正方形的面积是1,
∴直角三角形的斜边的平方为13,
∵直角三角形较短的直角边为a,较长的直角边为b,
∴a2+b2=13,
∵大正方形的面积减去小正方形的面积等于四个直角三角形的面积,
∴4×ab=13﹣1,即2ab=12,
∴(a+b)2=a2+2ab+b2=13+12=25.
18.(1)解:这个公式是完全平方公式:(a+b)2=a2+2ab+b2;理由如下:
∵大正方形的边长为a+b,
∴大正方形的面积=(a+b)2,
又∵大正方形的面积=两个小正方形的面积+两个矩形的面积=a2+b2+ab+ab=a2+2ab+b2,
∴(a+b)2=a2+2ab+b2;
故答案为:(a+b)2=a2+2ab+b2;
(2)证明:∵△ABC≌△CDE,
∴∠BAC=∠DCE,
∵∠ACB+∠BAC=90°,
∴∠ACB+∠DCE=90°,
∴∠ACE=90°;
(3)证明:∵∠B=∠D=90°,
∴∠B+∠D=180°,
∴AB∥DE,即四边形ABDE是梯形,
∴四边形ABDE的面积=(a+b)(a+b)=ab+c2+ab,
整理得:a2+b2=c2.
19.(1)证明:在Rt△ABC中,∠B=90°,∠ACB=30°,AB=2,
∴AC=2AB=4,
在△ACD中,AC=4,CD=3,AD=5,
∵42+32=52,即AC2+CD2=AD2,
∴∠ACD=90°,
∴AC⊥CD;
(2)解:在Rt△ABC中,∠B=90°,AB=2,AC=4,
∴BC==2,
∴Rt△ABC的面积为AB BC=×2×2=2,
又∵Rt△ACD的面积为AC CD=×4×3=6,
∴四边形ABCD的面积为:2+6.
20.解:(1)由题意有:n2﹣1,2n,n2+1;
(2)猜想为:以a,b,c为边的三角形是直角三角形.
证明:∵a=n2﹣1,b=2n;c=n2+1
∴a2+b2=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2
而c2=(n2+1)2
∴根据勾股定理的逆定理可知以a,b,c为边的三角形是直角三角形.
21.解:当n=1,a=(m2﹣1)①,b=m②,c=(m2+1)③,
∵直角三角形有一边长为5,
∴Ⅰ、当a=5时,(m2﹣1)=5,解得:m=(舍去),
Ⅱ、当b=5时,即m=5,代入①③得,a=12,c=13,
Ⅲ、当c=5时,(m2+1)=5,解得:m=±3,
∵m>0,
∴m=3,代入①②得,a=4,b=3,
综上所述,直角三角形的另外两条边长分别为12,13或3,4.
22.解:根据图表,由图可得规律:,解得.
所以b=84;c=85.
∵132+842=7225,852=7225,
∴13,84,85是勾股数.
1.如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标介于( )
A.0和1之间 B.1和2之间 C.2和3之间 D.3和4之间
2.如图,在边长为1个单位长度的小正方形网格中,点A、B都是格点(即网格线的交点),则线段AB的长度为( )
A.3 B.5 C.6 D.4
3.汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值是( )
A. B. C.3 D.
4.如图是我国古代数学家赵爽为了证明勾股定理,而构造的一个几何图形,称为赵爽弦图,如果在赵爽弦图的直角三角形中,有一个锐角是30°,则图中阴影部分的面积与大正方形面积的比是( )
A. B. C.﹣ D.
5.如图,一棵大树在离地面9米高的B处断裂,树顶A落在离树底BC的12米处,则大树断裂之前的高度为( )
A.9米 B.15米 C.21米 D.24米
6.如图,将一边长为a的正方形(最中间的小正方形)与四块边长为b的正方形(其中b>a)拼接在一起,则四边形ABCD的面积为( )
A.b2+(b﹣a)2 B.b2+a2 C.(b+a)2 D.a2+2ab
7.如图,△ABC的边BC在数轴上,AB⊥BC,且BC=3,AB=1,以C为圆心,AC长为半径画圆分别交数轴于点A′、点A″,那么数轴上点A′、点A″所表示的数分别是 、 .
8.如图,已知直角△ABC的两直角边分别为6,8,分别以其三边为直径作半圆,则图中阴影部分的面积为 .
9.如图,有赵爽弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=27,S3=1,则S1的值是 .
10.如图所示,由四个全等的直角三角形拼成的图中,直角边长分别为2,3,则大正方形的面积为 .
11.如图,已知AB=4,BC=3,AD=12,DC=13,∠B=90°,则四边形ABCD的面积为 .
12.如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将直角边AB折叠使它落在斜边AC上,折痕为AD,则BD= .
13.在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个周长为2+2的△ABC,并求它的面积.
14.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,
(1)在图①中,画一个面积为10的正方形;
(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.
15.如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
16.如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长;
(3)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
①请在x轴、y轴上找一点C,使△ABC为等腰三角形;(要求:用尺规画出所有符合条件的点,并用C1,C2,…, n在图中标出所找的点.只保留作图痕迹,不写作法)
②写出一个满足条件的在x轴上的点的坐标: ,写出一个满足条件的在y轴上的点坐标: .
17.如图的图形取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,试求(a+b)2的值.
18.观察、思考与验证
(1)如图1是一个重要公式的几何解释,请你写出这个公式 ;
(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°;
(3)伽菲尔德(任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在《新英格兰教育日志》上),请你写出验证过程.
19.如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
20.张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22﹣1 32﹣1 42﹣1 52﹣1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a= ,b= ,c= ;
(2)猜想:以a,b,c为边的三角形是否为直角三角形并证明你的猜想.
21.阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
22.观察下表
列 举 猜 想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
… …
13、b、c 132=b+c
请你结合该表格及相关知识,求出b,c的值,并验证13,b,c是否是勾股数?
参考答案
1.解:∵点A,B的坐标分别为(﹣2,0),(0,3),
∴OA=2,OB=3,
在Rt△AOB中,由勾股定理得:AB==,
∴AC=AB=,
∴OC=﹣2,
∴点C的坐标为(﹣2,0),
∵,
∴,
即点C的横坐标介于1和2之间,
故选:B.
2.解:由勾股定理得:AB==5;
故选:B.
3.解:将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=10,
∴得出S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=10,故3x+12y=10,
x+4y=,
所以S2=x+4y=,
故选:B.
4.解:设阴影部分的面积为s,直角三角形的两直角边分别是a、b,
∴小正方形的边长为,即b﹣a=,
∵直角三角形中较小的锐角为30°,
∴b=a,
解得:a=,b=,
∵大正方形的面积=c2=a2+b2,
∴大正方形的面积=()2+()2=(4+2)s.
∴阴影部分的面积与大正方形面积的比是:.
故选:D.
5.解:由题意得BC=9,在直角三角形ABC中,根据勾股定理得:AB=15米.
所以大树的高度是15+9=24米.
故选:D.
6.解:∵DE=b﹣a,AE=b,
∴S四边形ABCD=4S△ADE+a2=4××(b﹣a) b+a2
=b2+(b﹣a)2.
故选:A.
7.解:由勾股定理得,AC==,
则CA′=CA′′=,
∴OA′=﹣1,OA′′=+1,
∴A′、点A″所表示的数分别是1﹣和1+
故答案为:1﹣;1+.
8.解:在Rt△ABC中,AC=6,BC=8,
根据勾股定理得:AB==10,
则S阴影=S半圆AC+S半圆BC+S△ABC﹣S半圆AB=π+π+×6×8﹣π=24.
故答案为:24
9.解:∵八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,
∴CG=NG,CF=DG=NF,
∴S1=(CG+DG)2
=CG2+DG2+2CG DG
=GF2+2CG DG,
S2=GF2,
S3=(NG﹣NF)2=NG2+NF2﹣2NG NF,
∴S1+S2+S3=GF2+2CG DG+GF2+NG2+NF2﹣2NG NF=3GF2=27,
∴GF2=9,
∴S2=9,
∵S3=1,
∴S1的值是17.
故答案为17.
10.解:∵直角三角形的两条直角边长分别为2,3,
∴整个大正方形的边长为:=,
∴整个大正方形的面积为:13.
11.解:连接AC,
∵∠B=90°
∴AC2=AB2+BC2=16+9=25
∵AD2=144,DC2=169
∴AC2+AD2=DC2
∴CA⊥AD
∴S四ABCD=S△ABC+S△ACD=34+×125=36.
12.解:设点B落在AC上的E点处,连接DE,如图所示,
∵△ABC为直角三角形,AB=6,BC=8,
∴根据勾股定理得:AC==10,
设BD=x,由折叠可知:DE=BD=x,AE=AB=6,
可得:CE=AC﹣AE=10﹣6=4,CD=BC﹣BD=8﹣x,
在Rt△CDE中,
根据勾股定理得:(8﹣x)2=42+x2,
解得:x=3,
则BD=3.
故答案为:3.
13.解:△ABC是一个周长为2+2三角形,
△ABC的面积=3×4﹣×2×4﹣×1×3﹣×1×3=5.
14.解:(1)如图①所示:
(2)如图②③所示.
15.解:(1)∵BQ=2×2=4(cm),BP=AB﹣AP=16﹣2×1=14(cm ),∠B=90°,
∴PQ===(cm);
(2)BQ=2t,BP=16﹣t,
根据题意得:2t=16﹣t,
解得:t=,
即出发秒钟后,△PQB能形成等腰三角形;
(3)①当CQ=BQ时,如图1所示,
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.
③当BC=BQ时,如图3所示,
过B点作BE⊥AC于点E,
则BE==,
∴CE=,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
16.解:(1)由图可得,×(a+b)(a+b)=ab+c2+ab,
整理得,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
(2)当a=2,b=4时,
可得:c=;
如图1:
所以四边形的周长为:8+4;
(3)如图2:
一个满足条件的在x轴上的点的坐标:(﹣1,0);
一个满足条件的在y轴上的点的坐标:(0,2+).
故答案为:(﹣1,0);(0,2+),
17.解:∵大正方形的面积是13,小正方形的面积是1,
∴直角三角形的斜边的平方为13,
∵直角三角形较短的直角边为a,较长的直角边为b,
∴a2+b2=13,
∵大正方形的面积减去小正方形的面积等于四个直角三角形的面积,
∴4×ab=13﹣1,即2ab=12,
∴(a+b)2=a2+2ab+b2=13+12=25.
18.(1)解:这个公式是完全平方公式:(a+b)2=a2+2ab+b2;理由如下:
∵大正方形的边长为a+b,
∴大正方形的面积=(a+b)2,
又∵大正方形的面积=两个小正方形的面积+两个矩形的面积=a2+b2+ab+ab=a2+2ab+b2,
∴(a+b)2=a2+2ab+b2;
故答案为:(a+b)2=a2+2ab+b2;
(2)证明:∵△ABC≌△CDE,
∴∠BAC=∠DCE,
∵∠ACB+∠BAC=90°,
∴∠ACB+∠DCE=90°,
∴∠ACE=90°;
(3)证明:∵∠B=∠D=90°,
∴∠B+∠D=180°,
∴AB∥DE,即四边形ABDE是梯形,
∴四边形ABDE的面积=(a+b)(a+b)=ab+c2+ab,
整理得:a2+b2=c2.
19.(1)证明:在Rt△ABC中,∠B=90°,∠ACB=30°,AB=2,
∴AC=2AB=4,
在△ACD中,AC=4,CD=3,AD=5,
∵42+32=52,即AC2+CD2=AD2,
∴∠ACD=90°,
∴AC⊥CD;
(2)解:在Rt△ABC中,∠B=90°,AB=2,AC=4,
∴BC==2,
∴Rt△ABC的面积为AB BC=×2×2=2,
又∵Rt△ACD的面积为AC CD=×4×3=6,
∴四边形ABCD的面积为:2+6.
20.解:(1)由题意有:n2﹣1,2n,n2+1;
(2)猜想为:以a,b,c为边的三角形是直角三角形.
证明:∵a=n2﹣1,b=2n;c=n2+1
∴a2+b2=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2
而c2=(n2+1)2
∴根据勾股定理的逆定理可知以a,b,c为边的三角形是直角三角形.
21.解:当n=1,a=(m2﹣1)①,b=m②,c=(m2+1)③,
∵直角三角形有一边长为5,
∴Ⅰ、当a=5时,(m2﹣1)=5,解得:m=(舍去),
Ⅱ、当b=5时,即m=5,代入①③得,a=12,c=13,
Ⅲ、当c=5时,(m2+1)=5,解得:m=±3,
∵m>0,
∴m=3,代入①②得,a=4,b=3,
综上所述,直角三角形的另外两条边长分别为12,13或3,4.
22.解:根据图表,由图可得规律:,解得.
所以b=84;c=85.
∵132+842=7225,852=7225,
∴13,84,85是勾股数.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
