18.1.1 第2课时 平行四边形对角线的性质 练习题 2021-2022学年人教版八年级数学下册(word版含解析)
文档属性
| 名称 | 18.1.1 第2课时 平行四边形对角线的性质 练习题 2021-2022学年人教版八年级数学下册(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 157.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 08:12:49 | ||
图片预览



文档简介
18.1.1 第2课时 平行四边形对角线的性质
一、选择题
1.平行四边形的对角线一定具有的性质是( )
A.相等 B.互相平分
C.互相垂直 D.互相垂直且相等
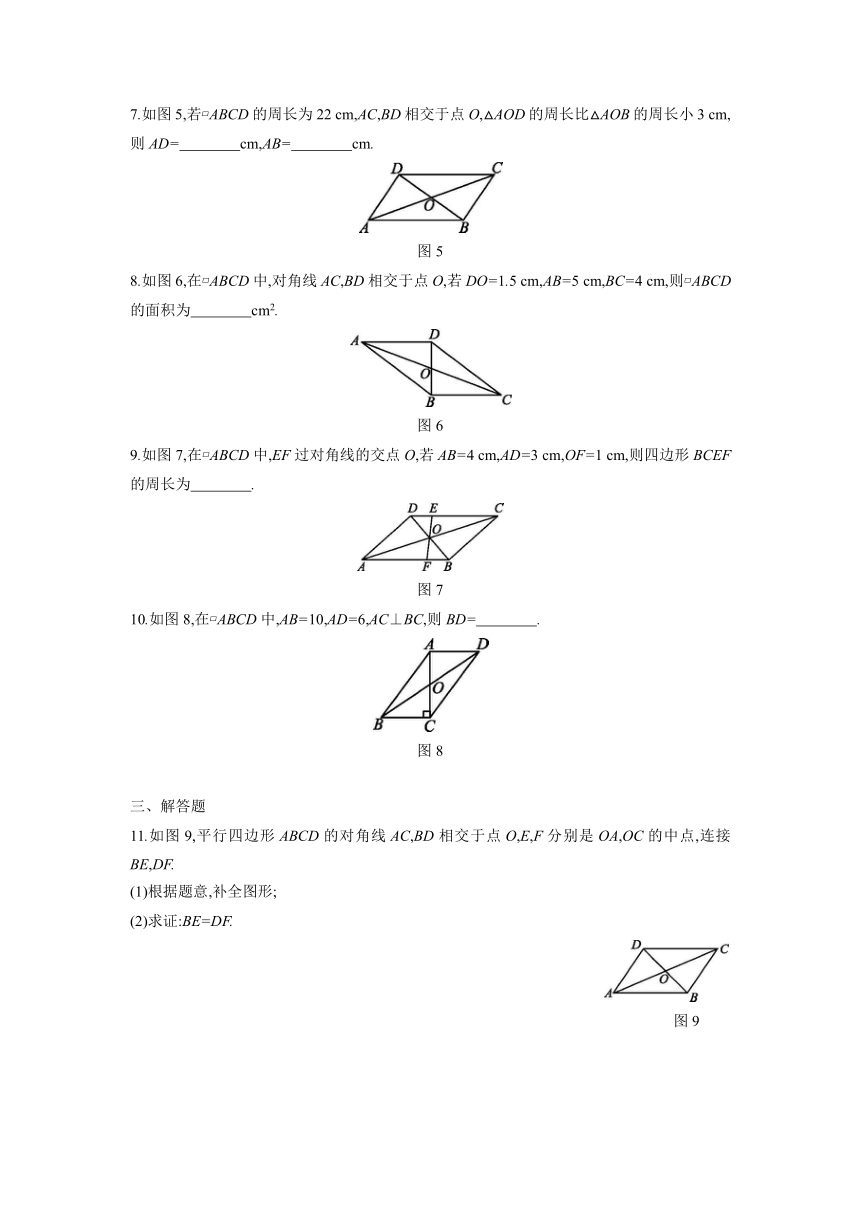
2.如图1, ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为 ( )
图1
A.13 B.17 C.20 D.26
3.平行四边形的一条边长是14 cm,它的两条对角线长可以是 ( )
A.12 cm,16 cm B.20 cm,22 cm
C.10 cm,16 cm D.14 cm,12 cm
4.如图2, ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则 ABCD的两条对角线的和是 ( )
图2
A.18 B.28 C.36 D.46
5.如图3,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O作OE⊥AC交AD于点E.若AE=12,DE=5,AB=13,则AC的长为 ( )
图3
A.12 B.16 C.18 D.14
二、填空题
6.如图4,已知在 ABCD中,对角线AC,BD相交于点O,△AOB的面积为2,那么 ABCD的面积为 .
图4
7.如图5,若 ABCD的周长为22 cm,AC,BD相交于点O,△AOD的周长比△AOB的周长小3 cm,则AD= cm,AB= cm.
图5
8.如图6,在 ABCD中,对角线AC,BD相交于点O,若DO=1.5 cm,AB=5 cm,BC=4 cm,则 ABCD的面积为 cm2.
图6
9.如图7,在 ABCD中,EF过对角线的交点O,若AB=4 cm,AD=3 cm,OF=1 cm,则四边形BCEF的周长为 .
图7
10.如图8,在 ABCD中,AB=10,AD=6,AC⊥BC,则BD= .
图8
三、解答题
11.如图9,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.
(1)根据题意,补全图形;
(2)求证:BE=DF.
图9
12.如图10,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线分别交DA,BC的延长线于点E,F.
求证:AE=CF.
图10
13.如图11,O是 ABCD的对角线AC的中点,过点O作一条直线与AB,CD分别交于点M,N,点E,F在直线MN上,且OE=OF,连接AE,CF.
(1)图中共有几对全等三角形 请把它们都写出来;
(2)求证:∠MAE=∠NCF.
图11
14.如图12,平行四边形ABCD的对角线AC,BD相交于点O,AC⊥AB,AB=2,且AC∶BD=2∶3.
(1)求AC的长;
(2)求△AOD的面积.
图12
15.已知:如图13,C为∠MON内一定点,过点C求作一直线AB,使其交OM于点A,交ON于点B,且AC=BC(写出作法).
图13
答案
1.B
2.B [解析] ∵四边形ABCD是平行四边形,
∴BC=AD,OA=OC,OB=OD.
又∵AD=8,BD=12,AC=6,
∴BC=8,OB=6,OC=3,
∴△OBC的周长=8+6+3=17.故选B.
3.B [解析] 平行四边形的对角线互相平分,平行四边形的一边和两条对角线的一半构成三角形,根据三角形的三边关系判断.
A项,6+8=14,故不能构成三角形;
B项,10+11>14,故能构成三角形;
C项,5+8<14,故不能构成三角形;
D项,7+6<14,故不能构成三角形.
故选B.
4.C [解析] ∵四边形ABCD是平行四边形,
∴AB=CD=5,BD=2OD,AC=2OC.
∵△OCD的周长为23,
∴OD+OC=23-5=18.
∵BD=2OD,AC=2OC,
∴ ABCD的两条对角线的和=BD+AC=2(OD+OC)=36.
故选C.
5.A [解析] 如图,连接CE.
∵四边形ABCD是平行四边形,
∴AO=CO,CD=AB=13.
∵OE⊥AC,
∴OE垂直平分AC,
∴CE=AE=12.
又∵DE=5,
∴CE2+DE2=122+52=132=CD2,
∴∠CED=90°,
∴∠AEC=90°,
∴AC===12.
6.8 [解析] ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD=BC,AB=CD,
∴△AOB≌△COD,△BOC≌△DOA,
∴S△AOB=S△COD,S△BOC=S△DOA.
∵AO是△ABD的中线,
∴S△AOB=S△DOA,
∴S△AOB=S△BOC=S△COD=S△DOA,
∴S ABCD=4S△AOB=4×2=8.
故答案为8.
7.4 7 [解析] 设AD的长为x cm,AB的长为y cm.
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OD=OB.
∵ ABCD的周长为22 cm,
∴AD+AB=11 cm,即x+y=11.①
∵OD=OB,且△AOD的周长比△AOB的周长小3 cm,
∴AD的长比AB的长小3 cm,即y-x=3.②
联立①②可得二元一次方程组解得
即AD=4 cm,AB=7 cm.
8.12 [解析] ∵四边形ABCD是平行四边形,
∴BD=2DO=2×1.5=3(cm),CD=AB=5 cm.
∵BC=4 cm,
∴BC2+BD2=CD2,
∴∠CBD=90°,即BD⊥BC,
∴S ABCD=BC·BD=4×3=12(cm2).
9.9 cm [解析] 由已知,可得 ABCD的周长为2×(3+4)=14(cm).
因为EF过 ABCD的对角线的交点O,
所以四边形BCEF的周长为EF+ ABCD周长的一半,即EF+7 cm.
又EF=2OF=2×1=2(cm),
所以四边形BCEF的周长为9 cm.
10.4 [解析] ∵四边形ABCD是平行四边形,∴BC=AD=6.
∵AC⊥BC,
∴∠ACB=90°.
在Rt△ABC中,AC===8.
∵平行四边形的对角线互相平分,
∴OC=AC=4,BD=2BO.
在Rt△OBC中,BO==2,
∴BD=2BO=4.
11.解:(1)如图所示.
(2)证明:∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,
∴OB=OD,OA=OC.
∵E,F分别是OA,OC的中点,
∴OE=OA,OF=OC,
∴OE=OF.
在△BEO和△DFO中,
∴△BEO≌△DFO(SAS),
∴BE=DF.
12.证明:∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,
∴AO=CO,AD∥BC,
∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF.
13.解:(1)图中共有4对全等三角形,分别为△AOM≌△CON,△AOE≌△COF,△AME≌△CNF,△ABC≌△CDA.
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠DCO.
∵O是AC的中点,
∴OA=OC.
在△AOE和△COF中,
∴△AOE≌△COF(SAS),
∴∠EAO=∠FCO,
∴∠EAO-∠BAO=∠FCO-∠DCO,
即∠MAE=∠NCF.
14.解:(1)∵AC⊥AB,
∴∠BAO=90°.
∵AC∶BD=2∶3,
∴设AC=2a,BD=3a.
∵四边形ABCD是平行四边形,
∴AO=AC=a,BO=BD=1.5a.
在Rt△BAO中,由勾股定理,得22+a2=(1.5a)2,
解得a=(负值已舍去),
则AC=2a=.
(2)由(1)知BO=DO,
∴S△ABO=S△AOD.
由(1)知AO=,
∴S△ABO=AB·AO
=×2×
=,
即S△AOD=.
15.解:作法:(1)连接OC并延长到点O',使CO'=OC;
(2)过点O'作O'A∥ON交OM于点A;
(3)过点O'作O'B∥OM交ON于点B;
(4)过点A,B作直线AB.
则直线AB就是所求作的直线,如图.
一、选择题
1.平行四边形的对角线一定具有的性质是( )
A.相等 B.互相平分
C.互相垂直 D.互相垂直且相等
2.如图1, ABCD的对角线AC,BD相交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为 ( )
图1
A.13 B.17 C.20 D.26
3.平行四边形的一条边长是14 cm,它的两条对角线长可以是 ( )
A.12 cm,16 cm B.20 cm,22 cm
C.10 cm,16 cm D.14 cm,12 cm
4.如图2, ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则 ABCD的两条对角线的和是 ( )
图2
A.18 B.28 C.36 D.46
5.如图3,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O作OE⊥AC交AD于点E.若AE=12,DE=5,AB=13,则AC的长为 ( )
图3
A.12 B.16 C.18 D.14
二、填空题
6.如图4,已知在 ABCD中,对角线AC,BD相交于点O,△AOB的面积为2,那么 ABCD的面积为 .
图4
7.如图5,若 ABCD的周长为22 cm,AC,BD相交于点O,△AOD的周长比△AOB的周长小3 cm,则AD= cm,AB= cm.
图5
8.如图6,在 ABCD中,对角线AC,BD相交于点O,若DO=1.5 cm,AB=5 cm,BC=4 cm,则 ABCD的面积为 cm2.
图6
9.如图7,在 ABCD中,EF过对角线的交点O,若AB=4 cm,AD=3 cm,OF=1 cm,则四边形BCEF的周长为 .
图7
10.如图8,在 ABCD中,AB=10,AD=6,AC⊥BC,则BD= .
图8
三、解答题
11.如图9,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.
(1)根据题意,补全图形;
(2)求证:BE=DF.
图9
12.如图10,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线分别交DA,BC的延长线于点E,F.
求证:AE=CF.
图10
13.如图11,O是 ABCD的对角线AC的中点,过点O作一条直线与AB,CD分别交于点M,N,点E,F在直线MN上,且OE=OF,连接AE,CF.
(1)图中共有几对全等三角形 请把它们都写出来;
(2)求证:∠MAE=∠NCF.
图11
14.如图12,平行四边形ABCD的对角线AC,BD相交于点O,AC⊥AB,AB=2,且AC∶BD=2∶3.
(1)求AC的长;
(2)求△AOD的面积.
图12
15.已知:如图13,C为∠MON内一定点,过点C求作一直线AB,使其交OM于点A,交ON于点B,且AC=BC(写出作法).
图13
答案
1.B
2.B [解析] ∵四边形ABCD是平行四边形,
∴BC=AD,OA=OC,OB=OD.
又∵AD=8,BD=12,AC=6,
∴BC=8,OB=6,OC=3,
∴△OBC的周长=8+6+3=17.故选B.
3.B [解析] 平行四边形的对角线互相平分,平行四边形的一边和两条对角线的一半构成三角形,根据三角形的三边关系判断.
A项,6+8=14,故不能构成三角形;
B项,10+11>14,故能构成三角形;
C项,5+8<14,故不能构成三角形;
D项,7+6<14,故不能构成三角形.
故选B.
4.C [解析] ∵四边形ABCD是平行四边形,
∴AB=CD=5,BD=2OD,AC=2OC.
∵△OCD的周长为23,
∴OD+OC=23-5=18.
∵BD=2OD,AC=2OC,
∴ ABCD的两条对角线的和=BD+AC=2(OD+OC)=36.
故选C.
5.A [解析] 如图,连接CE.
∵四边形ABCD是平行四边形,
∴AO=CO,CD=AB=13.
∵OE⊥AC,
∴OE垂直平分AC,
∴CE=AE=12.
又∵DE=5,
∴CE2+DE2=122+52=132=CD2,
∴∠CED=90°,
∴∠AEC=90°,
∴AC===12.
6.8 [解析] ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD=BC,AB=CD,
∴△AOB≌△COD,△BOC≌△DOA,
∴S△AOB=S△COD,S△BOC=S△DOA.
∵AO是△ABD的中线,
∴S△AOB=S△DOA,
∴S△AOB=S△BOC=S△COD=S△DOA,
∴S ABCD=4S△AOB=4×2=8.
故答案为8.
7.4 7 [解析] 设AD的长为x cm,AB的长为y cm.
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OD=OB.
∵ ABCD的周长为22 cm,
∴AD+AB=11 cm,即x+y=11.①
∵OD=OB,且△AOD的周长比△AOB的周长小3 cm,
∴AD的长比AB的长小3 cm,即y-x=3.②
联立①②可得二元一次方程组解得
即AD=4 cm,AB=7 cm.
8.12 [解析] ∵四边形ABCD是平行四边形,
∴BD=2DO=2×1.5=3(cm),CD=AB=5 cm.
∵BC=4 cm,
∴BC2+BD2=CD2,
∴∠CBD=90°,即BD⊥BC,
∴S ABCD=BC·BD=4×3=12(cm2).
9.9 cm [解析] 由已知,可得 ABCD的周长为2×(3+4)=14(cm).
因为EF过 ABCD的对角线的交点O,
所以四边形BCEF的周长为EF+ ABCD周长的一半,即EF+7 cm.
又EF=2OF=2×1=2(cm),
所以四边形BCEF的周长为9 cm.
10.4 [解析] ∵四边形ABCD是平行四边形,∴BC=AD=6.
∵AC⊥BC,
∴∠ACB=90°.
在Rt△ABC中,AC===8.
∵平行四边形的对角线互相平分,
∴OC=AC=4,BD=2BO.
在Rt△OBC中,BO==2,
∴BD=2BO=4.
11.解:(1)如图所示.
(2)证明:∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,
∴OB=OD,OA=OC.
∵E,F分别是OA,OC的中点,
∴OE=OA,OF=OC,
∴OE=OF.
在△BEO和△DFO中,
∴△BEO≌△DFO(SAS),
∴BE=DF.
12.证明:∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,
∴AO=CO,AD∥BC,
∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF.
13.解:(1)图中共有4对全等三角形,分别为△AOM≌△CON,△AOE≌△COF,△AME≌△CNF,△ABC≌△CDA.
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠DCO.
∵O是AC的中点,
∴OA=OC.
在△AOE和△COF中,
∴△AOE≌△COF(SAS),
∴∠EAO=∠FCO,
∴∠EAO-∠BAO=∠FCO-∠DCO,
即∠MAE=∠NCF.
14.解:(1)∵AC⊥AB,
∴∠BAO=90°.
∵AC∶BD=2∶3,
∴设AC=2a,BD=3a.
∵四边形ABCD是平行四边形,
∴AO=AC=a,BO=BD=1.5a.
在Rt△BAO中,由勾股定理,得22+a2=(1.5a)2,
解得a=(负值已舍去),
则AC=2a=.
(2)由(1)知BO=DO,
∴S△ABO=S△AOD.
由(1)知AO=,
∴S△ABO=AB·AO
=×2×
=,
即S△AOD=.
15.解:作法:(1)连接OC并延长到点O',使CO'=OC;
(2)过点O'作O'A∥ON交OM于点A;
(3)过点O'作O'B∥OM交ON于点B;
(4)过点A,B作直线AB.
则直线AB就是所求作的直线,如图.
